Экситонная оптическая нелинейность диэлектрических нанокомпозитов в слабых оптических полях

Необычные оптические свойства диэлектрических нанокомпозитных материалов активно исследуются в последнее десятилетие. Отдельное внимание уделяется особенностям, которые слабо выражены или отсутствуют в объемных диэлектриках. Например, выявлено дополнительное влияние свойств окружающей среды, внешнего поля, размера и характера формы частиц на спектры пропускания и люминесценции диэлектриков [1–3]. Схожее воздействие окружения наблюдается и для полупроводниковых наночастиц [4–6]. Также обнаружено в работах [7–10] появление нелинейного оптического отклика некоторых диэлектрических наноком-позитных материалов в диапазоне интенсивности порядка менее 1 кВт/см2, т.е. недостаточной для запуска многофотонных процессов, фотоионизации или других нелинейных процессов. В работах [11, 12] авторы, рассуждая о природе нелинейности такого типа, приходят к выводу, что причина в ключевом влиянии экситонных уровней в диэлектрических частицах на общий спектр пропускания. В работе [13] сформулированы условия, благоприятствующие возникновению устойчивых экси-тонных состояний в веществах, состоящих из диэлектрических наночастиц, внедренных в прозрачную жидкую диэлектрическую матрицу с линейными оптическими свойствами в оптическом диапазоне. Опубликованные в работах [14–19] результаты экспериментальных исследований таких веществ показали, что при интенсивности излучения около 150–250 Вт/см2 нелинейная добавка к показателю преломления вблизи резонансной частоты полосы поглощения составила nn = 104 ÷ 10-5. Это хорошо согласуется с предложенной в работе [20] теоретической моделью такой нелинейности. Вместе с тем для хорошего прогнозирования опти- оптика. – 2016. – Т. 40, № 6. – С. 855-862. – ческих свойств нанокомпозитных диэлектрических материалов необходимо исследовать влияние размеров, формы и концентрации наночастиц. В теоретических исследованиях оптической нелинейности используется численное решение уравнений Шредингера, например, в работах [21, 22]. Использование данного подхода для наносистем, состоящих из тысяч взаимодействующих элементов, крайне затруднительно даже для численного решения, поскольку увеличение количества взаимодействующих элементов значительно усложняет вид уравнения. Возможным путем решения проблемы может быть введение в уравнение функций, описывающих поведение каких-либо параметров системы согласно эмпирическим данным. Для такого подхода необходима согласованная с экспериментальными данными математическая модель физического процесса. В предыдущих работах [9, 13, 14, 17–20] сделана аппроксимация экси-тонного оптического отклика при различных параметрах, определенных эмпирически для каждого случая. Цель настоящей работы – развить описание модели с учетом новых условий определения параметров, взятых из ранее проведенных экспериментов.

Модель резонансного поглощения

Под диэлектрическими нанокомпозитами мы понимаем диэлектрические наночастицы, внедренные в жидкую прозрачную диэлектрическую матрицу с линейными оптическими свойствами в видимой области. В работах [14, 17–20] показано наличие в спектрах поглощений и люминесценции таких нанокомпозитов широких полос экситонного поглощения, лежащих внутри запрещенной зоны. Как правило, ярко выраженные пики экситонного поглощения для полупроводников наблюдаются при низких температурах (десятков К) [23, 24]. В диэлектрических нанокомпозитах экситон- ные полосы поглощения можно наблюдать и при температуре порядка 300 К. Это наблюдается тогда, когда длина волны Луи Де Бройля экситона сравнима с размерами наночастицы. При этом влияние раздела сред наночастица / матрица проявляется в виде увеличения глубины потенциальной ямы, в которой находится экситон (дырка и электрон), и приводит к увеличению энергии связи дырки и электрона. В классическом понимании это означает, что с внутренней стороны границы раздела сред возникает отрицательно заряженный слой, препятствующий разрушению экситона. Происходит это, если диэлектрическая проницаемость материала наночастицы больше, чем диэлектрическая проницаемость окружающей матрицы. Это приводит к тому, что экси-тонные линии поглощения сдвигаются вглубь запрещенной зоны и проявляются в полосах поглощения в видимом диапазоне, несмотря на большую (>6 эВ) энергию запрещенной зоны [19]. Выбор материалов наночастицы и окружающей матрицы необходимо делать не только с оценкой диэлектрической проницаемости на оптической частоте, но и с соблюдением прозрачности для уменьшения влияния теплового эффекта. Это также приводит к требованию низкой объемной концентрации. Высокая концентрация наночастиц, при которой будет происходить взаимодействие частиц друг с другом, нежелательна, так как это уменьшит величину нелинейного оптического отклика. Поэтому нами исследован случай с малой объемной концентрацией (порядка 0,3 %), что позволяет пренебречь взаимным влиянием между наночастицами и соблюсти условие прозрачности нанокомпозита. В слабых оптических полях вероятность двухфотонных процессов невелика, поэтому можем положить, что в квантовом представлении наночастицы представляют собой набор независимых двухуровневых систем, распределенных с объемной плотностью и независимо друг от друга взаимодействующих с окружением [25]. Для такой модели нелинейный оптический отклик среды пропорционален комплексной восприимчивости в единице объема, считая, что в диапазоне интенсивности до 1000 Вт/см2 полная восприимчивость вещества % представляется суммой линейной и экситонной нелинейной восприимчивости.

Х = Х о + Х R . (1)

Процесс создания экситона носит резонансный характер на определенных частотах. Поэтому мы должны воспользоваться моделью резонансной ком- плексной восприимчивости с разностью населенности уровней [26]:

-    Np ² Ар ng ( to, I )

X R =------ i g-----

ℏ

•

(to - too) + i Г (®-®о )2 +Г2,

^AP ng ( to , I ) = Ар ⁰

1 -

I / I s

(to-too )2 +Г2 (1 + I / Is )

где x 0 — линейная часть восприимчивости вещества, XR - резонансная нелинейная добавка к восприимчивости вещества, ω0 – частота резонанса, Г – полуширина линии поглощения, ħ – постоянная планка с чертой, N – число носителей заряда в объеме оптического пути, Ар ng – разность населенности уровней энергии состояний | n) и | g \ p = {n I e • ri | g) - проекция суммарного электрического дипольного момента перехода электронов наночастицы из состояния (n I в состояние | g) на направление поляризации внешнего оптического излучения, Аро - равновесная тепловая разность населенности при отсутствии внешнего поля, Is – уровень насыщения двухуровневой системы, при котором в возбужденное состояние перешла половина носителей зарядов. Отметим, что априори дипольный момент частицы неизвестен. Но в классическом смысле мы можем интерпретировать возбуждение экситона как перераспределение зарядов в наночастице и образование среднего дипольного момента dexc таким образом, что дипольный момент становится пропорциональным pо~a• e. При этом очевидно, что величина этого дипольного момента будет зависеть от размеров и формы наночастицы. Индуцированный дипольный момент dexc в наночастице в случае изотропного материала наночастиц может совпадать с вектором напряженности электрического поля Е, в случае же анизотропного материала суммарный дипольный момент наночастицы может не совпадать с Е, при этом возникает момент сил, который будет стремиться повернуть наночастицу вдоль вектора Е, что приведет к увеличению поляризации единицы объема. Отметим, что анизотропия наночастицы в процессе поляризации может присутствовать не только из-за свойств материала, но благодаря форме частицы. Момент сил ориентирования наночастицы будет пропорционален интенсивности внешнего поля. Параметр ориентации наночастицы вдоль поля будет являться сложной функцией от интенсивности I, который входит в них через дипольный момент и силы взаимодействия с внешним полем. Выражения для этой зависимости не представляется возможным аналитически записать. Однако справедливо ввести фактор ориентации A(I), который моделирует поведение квадрата дипольного момента при изменении интенсивности излучения:

p ² = p о ² A ( I ).                                         (4)

Зависимость фактора ориентации от интенсивности I задается в нашей работе в следующем виде:

A ( I ) = 1 - e ^- I ^{/ a} .                                          (5)

Форма наночастиц учитывается в модели через фактор ориентации вектора поляризации частицы вдоль вектора напряженности электрического поля, который зависит от интенсивности поляризованного излучения. Коэффициент α задает чувствительность к интенсивности излучения и определяется формой наночастиц, а точнее различием характерных размеров вдоль базисных векторов. Другими словами, величина этого коэффициента пропорциональна анизомерии наночастиц, что экспериментально наблюдалось в предыдущих исследованиях. Точный расчёт или аналитическое представление этого коэффициента через распределение размеров и форм наночастиц в объеме метаматериала с жидкой матрицей - открытый вопрос. Поэтому в описываемой модели этот коэффициент считается заданным параметром, и а^ 0 при сферичной форме наночастицы с изотропным тензором диэлектрической проницаемости.

Описание параметров моделирования с комплексным показателем преломления диэлектрических наночастиц в растворе:

nM I ) = ^п о + n n (ю, I) = ⁿ о + ^{(2 nX} r (ю, I))/ n о .       (7)

Для численного моделирования необходимо перечислить все вводимые параметры и обозначить их диапазон значений.

После преобразований выражений (3 - 5) перепишем выражение резонансной нелинейной добавки эк-ситонной восприимчивости в следующем виде:

NA (I) p о ² Ар ⁰ χ R        _ℏ

⋅

(ю — Мо) + i Г (ю-юо )2 +Г2 (1 +1 / Is )

.

• •    Ар о е [0,1] - равновесная тепловая разность населенности, в настоящей модели рассматривается случай стационарной температуры 300 К, поэтому можем полагать, что Ар о = const ;

• •    a е [5,100] нм - задаваемый размер диэлектрической наночастицы, нами исследован этот диапа-

Правая дробь выражения (6) представляет собой Лоренцеву модель в спектроскопии насыщения, в которой при Is = const реальная часть есть нечетная функция, а мнимая - четная. Зная, что восприимчивость X связана с диэлектрической проницаемостью, а вместе с этим с показателем преломления, отметим, что реальная часть выражения (6) задает нелинейную добавку к показателю преломления, а мнимая часть -добавку к коэффициенту поглощения вещества. Запишем выражение для связи восприимчивости XR зон размеров наночастиц;

• •    N е [1о¹²,1о¹⁵ ] см ^-3 - число носителей заряда в единице объема. В модели принимается равным числу наночастиц и рассчитывается через объемную концентрацию вещества и объём наночастицы при заданном размере a . Нами исследовался случай с объёмной концентрацией порядка f =0,3 %;

• •    p _о= a • e - максимальный дипольный момент наночастицы, где a - размер наночастицы, а заряд электрона e задан в системе СГС;

  
  
  
  
  
  

  1,0

  0,8

  0,6

  0,4

  0,2

  
  

  -- А^

  , Ap»g ,

  
  

  а=0,25 Х=532

  
  
  
  

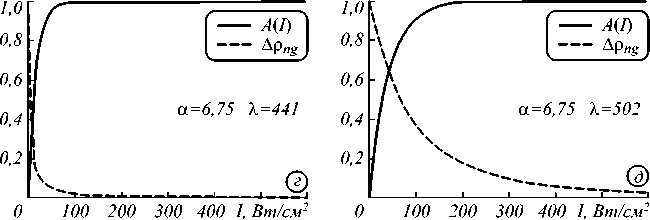
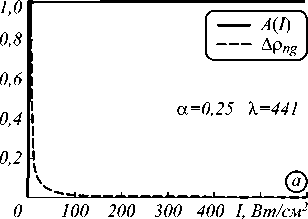
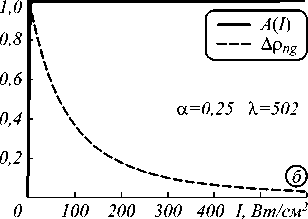
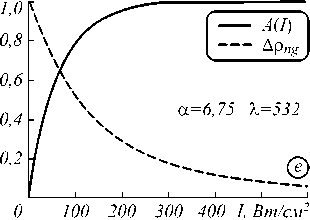
  Рис. 1. Диаграммы двух конкурирующих процессов: разность населенности ∆ρ ng и фактор ориентации A(I). Зависимость от интенсивности при фиксированной различных α и λ.

  Поведение соответствует сферической (а, б, в) и несферической (г, д, е) форме наночастиц

  
  

  100 200 300 400 I, Вт/см²

  
  
  

ю о , Г - резонансная частота и полуширина полосы поглощения, могут быть заданы из данных эксперимента. Для удобства в нашей модели отображается в размерности соответствующих им длинам волн Х_о и Г _х в нм;

n о - показатель преломления объемного вещества диэлектрических наночастиц на оптической частоте задается справочно;

ае [1,100] - коэффициент анизомерии наночастицы, при изотропном тензоре диэлектрической проницаемости и сферической форме наночастицы а^ о. Увеличение значений коэффициента означает, что один из ее базисных векторов превосходит другие;

• •    Is е [20,200] Вт / см² - порог насыщения, при котором фотоиндуцированно возбуждается половина свободных носителей заряда. Задается из данных эксперимента.

Поведение нелинейной восприимчивости удобно рассматривать как произведение двух конкурирующих процессов: фактора ориентации A(I) и разности населенности уровней Арng, графики которых изображены на рис. 1. Учет этих процессов необходим для выбора наиболее подходящего рабочего участка в применении экситонной нелинейности диэлектрических нанокомпозитов на практике, например, в оптических переключателях [27-29]. При анализе выражения (7) мож- но заметить, что значение величины восприимчивости χɶ R пропорционально N и p02 , которые, в свою очередь, задаются объёмной концентрацией f и размером наночастиц a.

А при f = const с увеличением размера частиц N уменьшается пропорционально a³ , а p ₀ ² увеличивается пропорционально a ². Это позволяет заключить, что при одинаковой объёмной концентрации уменьшение размера частиц ведёт к увеличению оптического нелинейного отклика. Как видно из выражений (3–5), нелинейная часть восприимчивости χ ɶ _R меняется от частоты и интенсивности.

Результаты моделирования

Через нелинейную восприимчивость и известные модели расчёта показателя преломления двухкомпозитной среды, например, модель Максвелла–Гарнетта, можно построить спектры пропускания, поглощения и рассеяния вещества. Выражения для расчёта спектров сечения рассеяния и поглощения вещества можно найти в работе [26]. Однако ввиду превосходства вклада линейной составляющей над нелинейной на несколько порядков целесообразно изображать отдельные спектры, соответствующие только нелинейной добавки к комплексному показателю преломления.

Для воспроизведения данных эксперимента [18] с частицами Al 2 O 3 , растворенными в прозрачном масле, в модель были заложены следующие значения параметров: ∆ρ ⁰ = 0,9, а =45 нм, n 0 = 1,65, λ 0 =437 нм, Г λ = 27,4 нм, f =0,3 %, Is =50 Вт/см², α = 3,5. На рис. 3 представлены графики комплексной нелинейной добавки n ɶ _n ( ω , Ι ) , достигающей 1,5· 10^–4 см²/Вт (рис. 2 г ). Рассмотрены случаи при фиксации длины волны (рис. 2 а – в ) или интенсивности (рис. 2 г – е ).

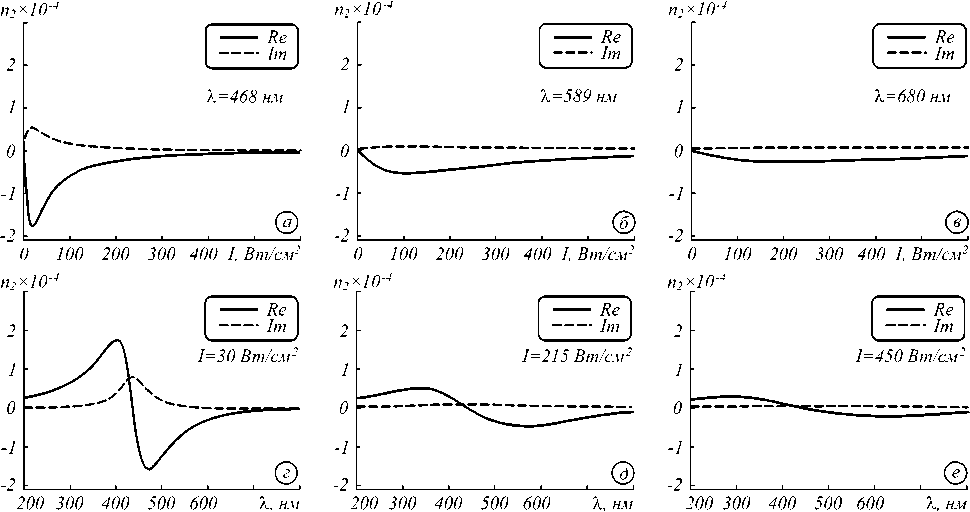
Рис. 2. Диаграммы нелинейной добавки при фиксированных λ (а, б, в) и фиксированных интенсивностях (г, д, е). Реальная и мнимая части показаны отдельно

Расчёты спектров длин волн показывают, что с изменением интенсивности мнимая часть нелинейной добавки уменьшается быстрей, чем реальная часть. При переходе через резонансную частоту λ0 реальная часть нелинейной добавки nɶn(ω, Ι) меняет знак. С изменением интенсивности (рис. 2г – е) наблюдается уширение полосы реальной и мнимой части nɶn (ω, Ι) с уменьшением амплитуды значений. Также на рис. 2а – в можно увидеть, что при удалении от резонансной частоты смещается экстремум в графиках интенсивности реальной и мнимой частей. Также на рис. 2а, б видно, что с ростом интенсивности нелинейный отклик сначала возрастает, а затем убывает. Такое уменьшение величины нелинейной добавки с ростом интенсивности объясняется влиянием процесса насыщения двухуровневой модели, когда уменьшается разность населенности уровней. Реальную и мнимую часть нелинейной добавки nɶn(ω, Ι) удобно оценивать в виде трёхмерных карт распределения от интенсивности и длины волны (рис. 3а, б).

Из анализа изображений хорошо видно распределение реальной части показателя преломления на различных длинах волн и интенсивностях. При относительно небольшой полуширине полосы поглощения площадь изменений нелинейной добавки реальной части охватывает большой оптический диапазон. Это означает, что наличие резонансной полосы поглощения в фиолетовой части спектра, имеющее экситонную природу, может быть использовано на значительном удалении до 200 нм от неё в красную область.

Заключение

Продемонстрировано поведение нелинейного эк- ситонного оптического отклика от интенсивности внешнего монохроматического излучения. Отличительная особенность заключается в том, что при плавном увеличении интенсивности излучения отклик сначала возрастает, а затем убывает.

а)   200 300 400 500 600 700

I, Вт/см2                           П2ХЮ'4

б)   200 300 400 500 600 700

Рис. 3. Реальная (а) и мнимая (б) части нелинейной добавки n2. Двумерная карта распределения значений нелинейной добавки от интенсивности и длины волны поляризованного излучения

Такое поведение экситонной нелинейности в диэлектрических нанокомпозитах отличает ее от известной квадратичной или кубической нелинейности вещества. Величина нелинейной добавки показателя преломления составляет до 1,5·10-4 при малой концентрации (до 0,3 %) и относительно низкой интенсивности излучения (до 1000 Вт/см2), представляет практический интерес для использования в оптических устройствах, например, в оптических транзисторах (трансфазорах) [30]. Представленная модель численных расчетов позволяет анализировать экситонную оптическую нелинейность на различных частотах и отслеживать поведение комплексной добавки nɶn(ω, Ι) при различных размерах частиц и других параметрах. Например, в результате численного моделирования установлено, что величина нелинейного оптического отклика χɶR пропорциональна размеру наночастиц и их количеству в единице объема N. При равной объемной концентрации наноча- стиц с уменьшением их размера возрастает величина χɶ R . Значит, для увеличения нелинейного оптического отклика рекомендуется использовать наночастицы меньшего размера. Установлено, что вклад в нелинейный оптический отклик фактора ориентации A(I) возрастает с увеличением анизомерии наночастиц. В наибольшей степени это проявляется вблизи резонансной частоты, а с отдалением от нее вклад нелинейного оптического отклика уменьшается. Также анизомерия наночастиц влияет на поведение нелинейного оптического отклика от интенсивности. При увеличении отношения размерных сторон частиц фактор ориентации имеет более медленный рост с увеличением интенсивности. Показано, что характер поведения нелинейного оптического отклика может служить индикатором сферичности частиц с изотропным тензором поляризуемости.

Работа выполнена при поддержке Программы фундаментальных исследований Дальневосточного отделения Российской академии наук, гранты (№ 0262-2015-0094, № 0262-2015-0059).