Экспериментальная апробация методов оценивания распределения кривизны оптического волокна

Контроль распределения кривизны (величина, обратная радиусу изгиба) оптического волокна (ОВ) представляет интерес для различных приложений. В частности, это актуально для оценки распределения избыточной длины волокна в модуле оптического кабеля (ОК). В модулях телекоммуникационного кабеля ОВ размещается с избыточностью, что позволяет снизить механические нагрузки на ОВ при растягивающих нагрузках, возникающих в процессе строительства и эксплуатации. Очевидно, что на степень равномерности распределения кривизны ОВ в кабеле будут влиять различные внешние факторы и в результате распределение радиусов изгиба вдоль кабеля носит случайный характер. При эксплуатации в условии низких отрицательных темпера- тур из-за значительной разницы в коэффициентах линейного расширения кварцевого стекла и материалов кабельных компонентов наблюдается уменьшение радиуса изгиба оптического волокна [1]. На кабельных линиях оценивание распределения кривизны волокна позволит выявить участки с недопустимо малыми радиусами изгиба, которые могут привести к снижению прочности ОВ и надежности. Особый интерес эта проблема приобрела в последние годы в связи с возможным применением маломодовых оптических волокон на линиях связи большой протяженности с точки зрения определения распределений коэффициентов связи мод.

В ряде работ [4–7] были предложены различные методы оценки распределения радиусов изгиба в ОВ. Следует отметить, что необходима адаптация подобных методов для практической реализации и современных нечувствительных к изгибам оптических волокон.

В данной работе проведена экспериментальная апробация методов с использованием стандартных коммерческих рефлектометров и их модификаций и определены ограничения методов.

Метод, основанный на измерении разности коэффициентов затухания на двух длинах волн

Один из методов оценки распределения кри- визны волокна основан на результатах измерения дополнительных потерь, вызванных изгибами волокна [2; 3]. На основании этого были предложены различные методы обнаружения изгибов волокон [4–6]. В данной работе реализована модификация метода, основанного на рефлектоме-трическом измерении на двух длинах волн 1550 и 1650 нм. На этих длинах волн оптическое волокно имеет разную чувствительность к изгибам, в то время как разница в коэффициентах затухания не столь значительна.

Расчет зависимости вносимых потерь в ОВ от радиуса изгиба на тестовых длинах волн может быть выполнен с использованием известной формулы и ее модификаций [2; 3]

П ии ² exp

к

2 w _

3 eg.  ,

« изг ( R ) =

e v W ^3,2VK_V - i ( wa ) K v + i ( wa ) ’

и² = k ² n²₀ -в . ; w ² = 3 . - k²n²_d ; k = 2n(X ;

₂— г      f2 ,    v = 0 ;

V = ka^n_co ^- n_cl ; e v =

где a - радиус сердцевины ОВ; n o , n l - показатели преломления сердцевины и оболочки соответственно; 3 _g - постоянная распространения моды; K_v – модифицированная функция Бесселя порядка v ; X - длина волны.

Данная формула не учитывает наличия осцилляций спектральной зависимости затухания из-за переотражений на границах оболочки и покрытия ОВ или между разными слоями ОВ при малых значениях радиуса изгиба. Критический радиус изгиба, при достижении которого необхо- димо учитывать осцилляции, можно определить по данным статьи [7] или экспериментально.

В работе было выполнено экспериментальное измерение спектра потерь на изгибах ОВ рек. МСЭ-Т G.657.A1/G.652.D и определено, что для изгибов ОВ с радиусом более 10 мм влиянием осцилляций можно пренебречь.

Кроме того, формула получена для стандартного ОВ со ступенчатым профилем показателя преломления и должна быть адаптирована для различных типов волокна, например, для оптического волокна рек. МСЭ-Т G.657.A1 с пониженной чувствительностью к потерям на изгибах. Для оценки корректирующих коэффициентов были проведены экспериментальные измерения для тестового образца оптического волокна G.657.A1/G.652.D. В результате были отмечены значительные расхождения количественных результатов расчета и эксперимента при сохранении качественных зависимостей.

Соотношение результатов расчета и измерений для диапазона длин волн 1530–1600 нм изменяется от 2,6 до 3,4 дБ по линейному закону.

Таким образом, можно экспериментальным путем определить поправочный коэффициент для расчетной формулы (1) или использовать полученные результаты при измерении на длинах волн, использованных при калибровке. Следует отметить, что в целом для оптических волокон различных торговых марок и производителей поправочные коэффициенты могут отличаться.

Для реализации предложенного метода рассчитывают коэффициенты, определяющие связь между радиусом изгиба и приращением коэффициента затухания, по следующему алгоритму:

– рассчитывается зависимость коэффициента затухания от радиуса изгиба для двух длин волн по формуле (1) и результат выражается в дБ/м;

– рассчитывается разность коэффициентов затухания Аа ( R , X 1 , Х ₂ ) ;

- логарифм Аа ( R , Х 1 , X₂ ) аппроксимируется линейной функцией в виде

log, (Аа(R,Xi,X2 )) = ^(Xi,Xd)R + B(Xi,X2);

– коэффициент аппроксимирующей кривой S ( X 1 , X₂ ) корректируется на основе экспериментальных измерений.

Алгоритм реализации метода:

– производится измерение с помощью оптического рефлектометра на двух длинах волн 1550 и 1650 нм (длительность импульса и время усреднения выбираются таким образом, чтобы уровень шума не превышал 0,1 дБ);

– выделяется участок рефлектограммы между концом мертвой зоны на входе и началом отражения от концa ОВ и нормируется для компенсации потерь на локальных событиях, таких как сварные соединения;

– вычисляется распределение коэффициента затухания по длине ОВ методом «скользящего

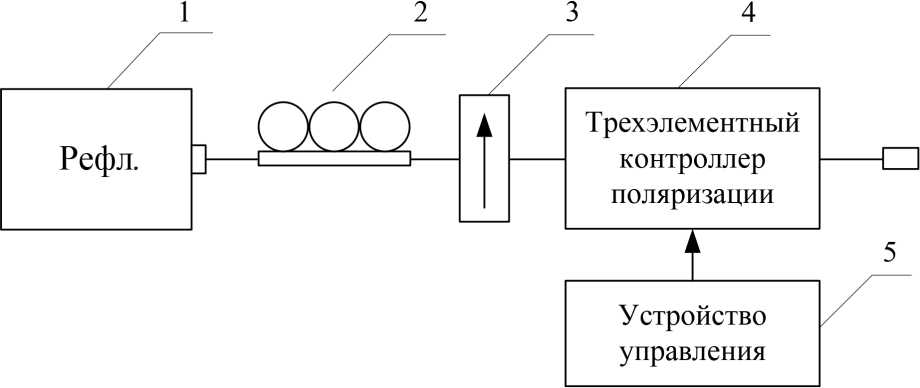
Рисунок 1. Структурная схема макета поляризационного оптического рефлектометра

окна» с использованием линейной аппроксимации методом наименьших квадратов (размер окна выбирается в пределах от 100 до 200 м);

– вычисляется распределение разности коэффициентов затухания на двух длинах волн;

– рассчитывается распределение радиусов изгиба, используя коэффициенты S ( X , , X 2 ) и B ( X , , X 2 ) , характеризующие соотношение между радиусом изгиба и приростом коэффициента затухания ОВ.

Метод, основанный на измерении распределения двулучепреломления поляризационным рефлектометром

Известно, что изгибы ОВ приводят к появлению наведенного двулучепреломления [8]. Для распределенного измерения двулучепреломления могут быть использованы методы поляризационной оптической рефлектометрии [9–11].

Для апробации метода, разработанного на основе подхода [10] и представленного в работе [12], собран макет поляризационного оптического рефлектометра, структурная схема которого представлена на рисунке 1. Макет реализован на базе стандартного оптического рефлектометра (1). Согласующий волоконно-оптический контроллер поляризации (2) служит для согласования состояния поляризации излучения зондирующего сигнала и ориентации оптической оси линейного поляризатора (3).

Линейный волоконно-оптический поляризатор служит для обеспечения чувствительности фотоприемного устройства к состоянию поляризации поступающего потока обратного рассеяния. Трехкаскадный контроллер поляризации (4) служит для преобразования состояния поляризации зондирующего излучения и сигнала обратного рассеяния в соответствии с заданными установками. Используемый в схеме контроллер реализован на основе последовательно соединенных трех двулучепреломляющих элементов с пе- рестраиваемой величиной двулучепреломления, при этом главные оптические оси элементов взаимно ориентированы в конфигурации 0°, 45°, 0°. Для работы совместно с трехкаскадным контроллером поляризации было разработано устройство управления (5), формирующее управляющие сигналы в соответствии с заданной конфигурацией фазовых задержек элементов контроллера.

Алгоритм реализации метода:

– выполняются измерения поляризационных характеристик обратного рассеяния для 6 вариантов величин фазовых задержек установок трехкаскадного контроллера поляризации;

– для каждой точки ПХОР вычисляются три разностные характеристики, определяемые выражениями:

Qi,k = Pk {0,0,0}-Pk (я,0,0};

Qi* = Pk {л / 2,0,0}-Pk {3л / 2,0,0};

Q3, k = Pk {0, л / 2,0}-Pk {л, л / 2,0}, где P {у,, V2, V2} — уровень поляризационной характеристики при заданных установках контроллера поляризации; уj — величина фазовой задержки j-го каскада контроллера поляризации; k – порядковый номер точки рефлектограммы;

– для каждой точки ПХОР вычисляется значение эквивалентного угла ориентации оптической оси q_k и значение локального двулучепреломления 5 _k к -го участка ОВ по формулам:

( Q, )

2qk = arctg       , v Q3,k о        . f      Q1, k^

5k=arctg т;-----лгч ;

V Q 2 , _t ^cos ( ² q k ) J

– учитывая, что каждой точке поляризационной характеристики обратного рассеяния соответствует интегральный поток обратнорассеянного излучения с участка ОВ, длина которого определяется пространственной длительностью

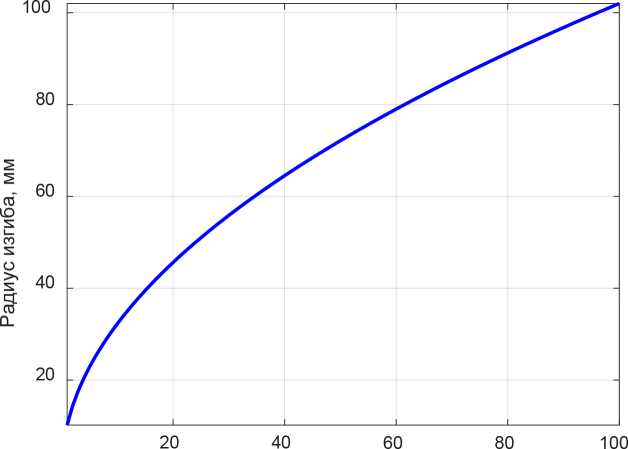
Длительность импульса, нс

Рисунок 2. Зависимость минимального значения выявляемого радиуса изгиба от длительности импульса (длина волны 1550 нм)

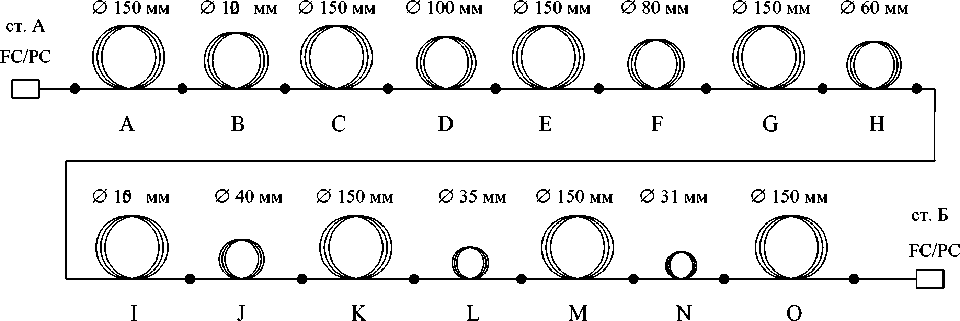
Рисунок 3. Схема расположения бухт ОВ

зондирующего импульса, производится расчет коэффициента локального двулучепреломления в к =

5 кПд ^ c т ’

где c – скорость оптического излучения в вакууме; n_g – групповой показатель преломления ОВ; т - длительность зондирующего импульса;

– предполагая, что основной вклад в двулучепреломление вносят изгибы, производится оценка локального радиуса изгиба

R k = г.

’ ^C s =      ( Р 11 — Р 12 ) ( 1 + v p ) ^{; (8)}

2р к        ^

где r – радиус оптического волокна; n ₀ – показатель преломления; p 11 , p ₁₂ - коэффициенты Поккельса для плавленого кварца; v_p – отношение Пуассона.

Необходимо отметить, что предложенный метод работоспособен при условии, что на каждом шаге расчета величина наведенного локального двулучепреломления ОВ не превышает п / 2. Учитывая соотношения в формуле (7) можно определить максимальное значение коэффициента двулучепреломления и соответствующее значение минимального радиуса изгиба, которые возможно оценить данным методом при заданной длительности импульса. На рисунке 2 приведены вычисленные значения минимального радиуса изгиба, которые можно корректно измерить для заданной длительности импульса.

Кроме того, ограничивающим фактором является вклад собственных шумов фотоприемного устройства рефлектометра. Для корректной оценки требуется обеспечение таких условий, чтобы размах шумовой составляющей характеристики обратного рассеяния составлял не более 0,05÷0,1 дБ.

Также на точность оценки влияет ширина спектра источника излучения рефлектометра. Лазерные диоды Фабри – Перо, используемые в стандартных рефлектометрах, могут иметь ширину спектра порядка 10 нм, что приводит к существенной деполяризации потока обратного рассеяния. В качестве решения данной проблемы могут применяться узкополосные лазерные диоды с распределенной обратной связью.

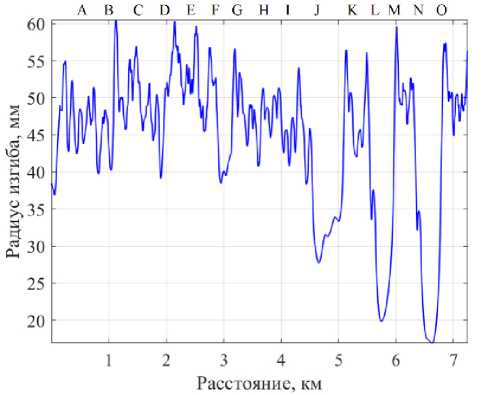
Рисунок 4. Результаты оценки распределения радиусов изгиба (метод измерения на двух длинах волн)

Для испытания предложенных методов был изготовлен макет, включающий бухты ОВ с различными значениями диаметра намотки (рисунок 3). Бухты формировались таким образом, чтобы после намотки и извлечения оправки ОВ находилось в свободном состоянии, а также не испытывало растягивающих усилий и микроизгибов из-за перехлестов ОВ. Макет состоит из 15 бухт ОВ, при этом 7 из них являются исследуемыми бухтами с различными заданными диаметрами намотки, а остальные являются буферными и включаются в начале и конце макета, а также между исследуемыми бухтами. Для исследования были изготовлены бухты путем намотки на оправки диаметром 120, 100, 80, 60, 40, 35 и 31 мм. Следует отметить, что при намотке на оправки малых диаметров значительных длин ОВ радиус изгибов для внутренних и внешних витков бухты будет заметно отличаться. Диаметр намотки буферных бухт одинаковый и в среднем составляет 150 мм. Для изготовления исследуемых бухт используется ОВ рек. МСЭ-Т G.657.A1/G.652.D.

На рисунке 4 приведены результаты оценки распределения радиусов изгиба, полученные в результате измерения на двух длинах волн при длительности импульса 30 нс.

В результате анализа полученных зависимостей можно сделать следующие заключения:

– для бухт с идентификаторами J, L, N измеренные значения радиусов изгиба согласуются с фактическими значениями радиусов намотки;

– результаты измерения с двух направлений совпадают;

– для бухт ОВ с радиусом намотки более 30 мм корректно оценить радиус изгиба данным методом невозможно.

Расстояние, км

б

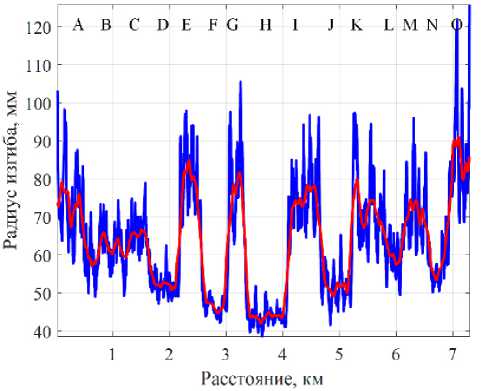
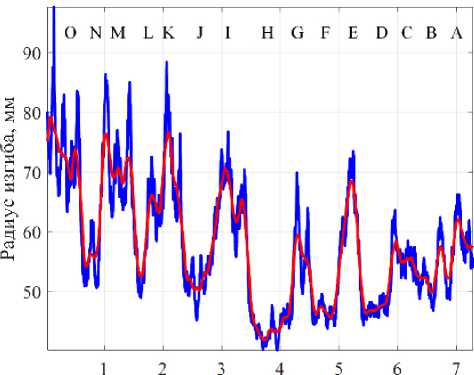
Рисунок 5. Распределение радиусов изгиба по результатам измерения поляризационным рефлектометром при длительности импульса 10 нс: а – направление ст. А – ст. Б; б – направление ст. Б – ст. А

На рисунках 5 и 6 приведено сравнение результатов определения радиуса изгиба ОВ на основе измерения поляризационным рефлектометром на макете № 1 для двух значений длительности импульса: 10 и 30 нс, соответственно.

Анализируя полученные зависимости, можно отметить следующие особенности:

– для направления А-Б при длительности импульса 10 нс получены значения радиусов изгибов, которые хорошо согласуются с реальными значениями радиусов намотки для всех буферных бухт и для бухт с идентификаторами B, D, F (средние значения радиусов изгибов 65, 55 и 45, соответственно);

– для направления А-Б при длительности импульса 10 нс для бухты H со средним радиусом намотки 35 мм полученное экспериментально

1       2       3      4      5      6       7                           1      2       3      4      5       6       7

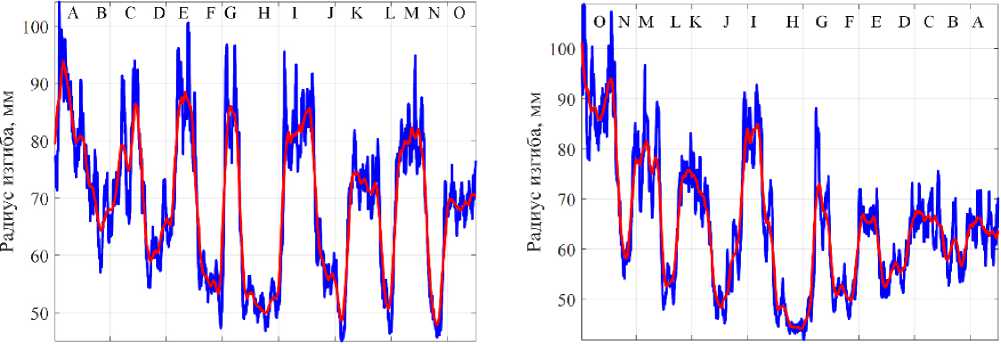
Расстояние, км                                            Расстояние, км а                                                   б

Рисунок 6. Распределение радиусов изгиба по результатам измерения поляризационным рефлектометром при длительности импульса 30 нс: а – направление ст. А – ст. Б; б – направление ст. Б – ст. А

значение составило в среднем 40 мм, что подтверждает рост погрешности измерения при нарушении требуемого соотношения «коэффициент двулучепреломления/длительность импульса»;

– для направления А-Б при длительности импульса 10 нс для бухт с идентификаторами J, L и N получены значения радиусов изгибов, превышающие фактический радиус намотки, что может объясняться тем, что, согласно расчетным данным, для данной длительности импульса минимальное значение детектируемого радиуса намотки составляет порядка 35 мм;

– для направления Б-А при длительности импульса 30 нс получены результаты, которые качественно соответствуют порядку расположения бухт с различными радиусами намотки, в частности для бухт с идентификаторами от A до I. Однако, если для буферных бухт A, C, E, G c радиусами намотки от 150 мм полученные значения радиусов изгибов согласуются с фактическими, то для бухт с идентификаторами B, D, F и H полученные значения радиусов изгибов превышают фактические;

– для направления Б-А при длительности импульса 10 нс получены значения радиусов изгибов, которые хорошо согласуются с реальными значениями радиусов намотки для буферных бухт с идентификаторами O, M, K и для бухт с идентификаторами D, F и H;

– для направления Б-А при длительности импульса 30 нс получены значения радиусов изгибов, которые качественно согласуются с реальными значениями радиусов намотки для буферных бухт с идентификаторами O, M и для бухт с идентификаторами В, D, F и H.

Заключение

В результате экспериментальной апробации методов были сделаны следующие выводы: метод, основанный на рефлектометрическом измерении на двух длинах волн, работоспособен при оценивании радиусов изгиба менее 30 мм; из-за особенностей анализа методом скользящего окна при требовании размеров окна порядка 100–200 м имеет низкую пространственную разрешающую способность; метод, основанный на измерении распределения двулучепреломления и реализованный с использованием макета поляризационного рефлектометра, разработанного на базе стандартного рефлектометра, продемонстрировал возможность оценивания радиусов изгибов величиной от 35 до 75 мм; определены ограничения метода, связанные с используемой длительностью импульса и типом лазерного диода.