Экспериментальная калибровка параметров контактной модели цифрового двойника почвенной среды методом дискретных элементов

Введение. На сегодняшний день метод дискретных элементов рассматривается как один из наиболее перспективных подходов для моделирования процессов, связанных с обработкой почвы и посевом, выполняемыми рабочими органами сельскохозяйственной техники. Цифровой двойник почвенной среды при моделировании методом дискретных элементов – это цифровая модель, которая наиболее точно воспроизводит физические и механические свойства реальной почвы с заданными параметрами. Параметры контактной модели цифрового двойника при моделировании почвенной среды методом дискретных элементов задаются при моделировании в программном комплексе ROCKY DEM. Для этого необходимо провести процесс калибровки с корректировкой параметров для достижения максимального соответствия между натурными и модельными экспериментами.

Калибровке параметров физических и механических свойств различных реальных почв для моделирования процесса обработки сельскохозяйственными рабочими органами посвящены многие исследования зарубежных ученых [1–3], в том числе с применением метода дискретных элементов [4–6]. Процесс проведения экспериментов заключается в моделировании почвенной среды с созданием виртуального почвенного канала с характеристиками реальной почвенной среды. Экспериментальные результаты исследований показывают, что изменение размеров модели цифрового двойника почвенного канала не оказывает существенного влияния на конечные результаты, если параметры модели настроены и откалиброваны правильно. Сравнение результатов моделирования и натурных опытов показывает хорошее качественное и количественное соответствие.

В экспериментальных исследованиях представлены результаты по моделированию в почвенном канале глубоко-рыхлителя методом дискретных элементов [7]. Авторы анализируют, как изменение гранулометрического состава почвенных частиц с диаметров от 14 мм до 18 мм с коэффициентом Пуассона грунта 0,35 влияет на тяговое сопротивление. При этом была проведена предварительная подготовка почвенного канала, которая включала увлажнение слоев почвы и послойное уплотнение [7].

Для калибровки параметров контактной модели используется комбинация методов пенетрациии и сдвига почвы для определения физико-механических свойств почвы путем внедрения наконечника на определенную глубину для почв различного механического состава, таких как крупной песок, суглинистый песок, супесь [8]. При этом для натурных экспериментов использовался почвенный канал с открытой и закрытой частью с длиной 40 м, шириной 2,7 м, глубиной 1,5. При этом виртуальная модель почвенного канала выполнена с шириной 0,6 м, длиной 0,6 м и высотой 0,2 м для исследования технологического процесса работы стрельчатой лапы. Для калибровки параметров был создан цифровой двойник процесса испытания кольца на сдвиг при кручении с областью расчетов с шириной 0,24 м, с длиной 0,24 м и высотой 0,15 м [8].

В ряде исследований [9, 10] для калибровки параметров контактной модели используются комбинации натурных экспериментов по определению угла естественного откоса и пенетрации почвы путем внедрения наконечников с плоским и конусным острием и с сопоставлением результатов с моделированием в про- граммном комплексе, проведенных методом дискретных элементов. Установлено, что уменьшение диаметра почвенных частиц с 20 мм до 10 мм с коэффициентом Пуассона почвы 0,3 дает более точные результаты когезии и угла трения между частицами почвы [9, 10]. При этом необходимо учитывать толщину слоя частиц. Так, при диаметре частиц в 3 мм и толщине слоя в 2 см, а в основании частицы диаметром 20 мм цифровой двойник показал более точные результаты по созданию профиля борозды [11–13].

В ряде наших исследований [14, 15] представлены результаты калибровки физико-механических параметров частиц модели почвенной среды, описываемых методом дискретных элементов. При этом калибровка параметров проведена по определению угла естественного откоса различных типов почвы. В качестве контактной модели была использована усовершенствованная модель Hertz-Mindlin JKR, которая была реализована в программном комплексе Rocky DEM. В работе представлена номограмма для выбора значений поверхностной энергии и диаметра почвенной частицы (particles) в зависимости от типа почвы и её влажности, которая позволяет моделировать процесс обработки почвы с достаточно высокой степенью точности [14, 15].

Анализ литературных источников показывает, что основной метод калибровки параметров контактной модели почвы осуществляется путем сравнения результатов физических и модельных экспериментов, касающихся усилия пе-нетрации, угла естественного откоса, по срезу реальной почвы и моделируемой почвенной среды. Экспериментальные результаты, полученные с использованием метода дискретных элементов, особенно в оценке сопротивления рабочих органов почвообрабатывающих и по- севных машин, в значительной степени зависят от корректной калибровки параметров дискретных почвенных частиц. Эти параметры должны учитывать конкретные почвенные условия и выбранную контактную модель. Однако в неполной мере описываются калибровочные тесты по определению зависимости усилия пенетрации почвы при изменении влажности определения параметров.

Цель данного исследования – экспериментальная калибровка параметров контактной модели для разработки цифрового двойника технологического процесса обработки почвы методом дискретных элементов.

Задачи исследования:

– провести калибровку параметров контактной модели Герца-Миндлина JKR для моделирования поведения почвы – чернозема легкосуглинистого механического состава;

– разработать номограмму для выбора параметров контактной модели Герца-Миндлина JKR в зависимости от влажности почвы.

Материалы и методы исследования. При создании точных моделей почвенной среды с использованием метода дискретных элементов (МДЭ) требуется провести калибровку параметров контактных моделей с использованием наиболее часто применяемого метода калибровки путем натурных и модельных экспериментов на угол естественного откоса реальной почвы и почвенной среды. Однако такой метод не позволяет учитывать прочностные характеристики и сопротивление деформации почвы. Поэтому нами предлагается провести калибровку параметров выбранной модели контакта по усилиям пенетрации исследуемых почв и сравнение полученных значений с результатами идентичной МДЭ-модели пенетрометра. Определе- ние усилия пенетрации почвы позволяет сразу установить силу, необходимую для внедрения рабочего наконечника в почву на определённую глубину, а это в свою очередь дает возможность оценить её плотность и сопротивление деформации. Данный параметр используется для анализа механических свойств почвы, таких как твёрдость и уплотнённость.

Для проведения натурного эксперимента по определению усилия пене-трации отбор проб производился в 5 точках, выбранных случайным образом с участков площадью 30 м2 с глубины 0,1, 0,2 м. Затем наполняли данной почвой цилиндрическую емкость высотой 220 мм и диаметром 125 мм.

Влажность почвы влияет на её физико-механические свойства, что, в свою очередь, определяет величину усилия пенетрации. Соответственно добивались различной влажности путем добавления воды и размешивания. При этом произ- водили отбор проб в металлические бюк-сы для определения влажности почвы.

Определение влажности почвы производили по ГОСТ 28268-89. Почвы. Методы определения влажности. Заключается в отборе образца почвы, его взвешивании до и после высушивания в сушильном шкафу при температуре 105 °C до постоянной массы (рисунок 1). Потеря массы образца после высушивания соответствует количеству испарившейся влаги. Влажность почвы рассчитывается как отношение массы потерянной влаги к массе сухого образца, выраженное в процентах.

Массовое отношение влаги в почве в процентах вычисляют по формуле

(Х Влаж.п - Х Сух.п. )

ω =                  ∙ 100,

Х ВС.П. - Х Б.

где Х Влаж.п. – масса влажной почвы с бюк-сой (масса влажного образца), г;

Х Сух.п. – масса сухой почвы с бюксой (масса сухого образца), г;

Х Б. – масса пустой бюксы, г.

Рисунок 1 – Определение влажности почвы в сушильном шкафу Figure 1 – Determination of soil moisture in a drying cabinet

Определение усилия пенетрации проводилось пенетрометром статического действия ПСГ-МГ4 производства ООО «СКБ Стройприбор» г. Челябинск (рису- нок 2). Измерение проводилось в соответствии с рабочими условиями, указанными в Руководстве по эксплуатации КБСП.427333.037 РЭ: температура окру- жающего воздуха 22 °С, относительная влажность воздуха 53%, атмосферное давление 670 мм рт. ст. Для калибровки физикомеханических параметров была выбрана черноземная почва легкосуглинистого механического состава. Чернозёмные почвы легкосуглинистого механического состава широко распространены в Российской Федерации, особенно в регионах с благоприятными условиями для формирования чернозёмов. Чернозёмы легкосуглинистого состава содержат 20–30% глинистых частиц, что дела- ет их плодородными почвами. Они обладают хорошей структурой, высокой влагоудерживающей способностью и богатым содержанием гумуса.

Пенетрометр работает за счет преобразования деформации упругого элемента тензодатчика, возникающей под воздействием прикладываемой силы, в электрический сигнал. Этот сигнал фиксируется электронным блоком 1, затем обрабатывается, и результаты измерения выводятся на цифровое табло 5 в единицах силы.

1 – электронный блок; 2 – тензометрическое силоизмерительное устройство;

3 – удлинительная штанга; 4 – рабочий наконечник; 5 – цифровое табло; 6 – кнопки управления Рисунок 2 – Пенетрометр статического действия ПСГ-МГ4

1 – electronic unit; 2 – strain gauge; 3 – extension rod; 4 – working tip;

5 – digital display; 6 – control buttons

Figure 2 – Static action Penetrometer PSG-MG4

Для исследования применяются рабочие наконечники с номинальным значением диаметра основания 22,0 мм; 16,0 мм; 11,3 мм; 8,0 мм; 6,0 мм (рисунок 3). Выбор рабочего наконечника производится в зависимости от усилий: в случае если сила будет более 550 Н, то необходимо установить рабочий наконечник с меньшим диаметром.

На рисунке 4 представлено проведение натурного эксперимента по определению усилия пенетрации почвы. Для этого рабочий наконечник плавно внедрялся в почву в течение 5–10 секунд до звукового сигнала. После этого на дисплее выводится среднее арифметическое значение измеряемого параметра.

p

0 6

Наконечник диаметром 6 мм Tip with a diameter of 6 mm

Наконечник диаметром 8 мм Tip with a diameter of 8 mm

Наконечник диаметром 11,3 мм Tip with a diameter of 11,3 mm

Наконечник диаметром 16 мм Tip with a diameter of 16 mm

Наконечник диаметром 22 мм Tip with a diameter of 22 mm

Рисунок 3 – Рабочие наконечники Figure 3 – Working tips

Рисунок 4 – Проведение натурного эксперимента по определению усилия пенетрации почвы Figure 4 – Conducting a field experiment to determine the force of soil penetration

Для каждого образца с различной влажностью проводилось измерение с 5-кратной повторностью. В соответствии с руководством по эксплуатации КБСП.427333.037 РЭ для измерения использовался рабочий наконечник диаметром 22 мм. Перед началом измерений была проведена калибровка зависимости ρ(P) между плотностью почвы и сопротивлением пенетрации.

После измерения данные архивируются в электронном блоке пенетрометра. Затем его подсоединяют к компьютеру через USB-соединение в специализированной программе для передачи данных и обработки (версия 1.0.0.1). На рисунке 5 представлено окно программы для передачи данных с приборов ПСГ-МГ4.

Рисунок 5 – Окно программы для передачи данных с приборов ПСГ-МГ4 Figure 5 – Program window for data transmission from PSG-MG4 devices

В окне специализированной про-

В ходе реализации калибровочного

граммы отражаются номер, дата и время проведения исследования. Имеется возможность импортирования данных в Excel.

Моделирование технологического процесса определения усилия пенетра-ции почвенной среды производилось в программном комплексе Rocky DEM. В качестве контактной модели была выбрана усовершенствованная модель Герца-Миндлина JKR [14, 15], в которой в качестве основной модели для нормальных сил используется модель контакта Герца, для тангенциальных сил – модель Миндлина-Дересевича, а для учета сил сцепления почвенных частиц – модель Johnson-Kendall-Roberts (JKR).

теста по определению усилия пенетрации R z почвенной среды методом дискретных элементов было установлено, что изменение значений поверхностной энергии, характеризующей адгезионную силу почвенных частиц, действующих как смазка между почвенными частицами (particles), влияет на усилие проникновения рабочего наконечника через дискретные почвенные частицы (particles), как и влажность ω на усилие пенетрации реальной почвы в натурных экспериментах.

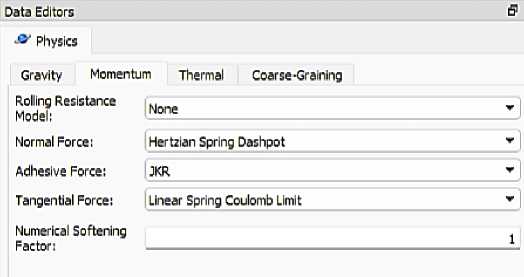
На рисунке 6 представлена настройка параметров в программном комплексе RockyDEM.

а а

б b

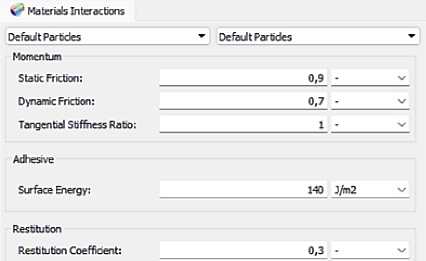
а – выбор контактной модели для физических свойств почвенной среды; б – параметры контактной модели

Рисунок 6 – Настройка параметров в программном комплексе RockyDEM a – selection of a contact model for the physical properties of the soil environment; b – contact model parameters

Figure 6 – Parameter setting in the RockyDEM software package

Таким образом, можно предположить, что изменение поверхностной энергии Gs в цифровом двойнике позволит предсказывать изменение влажности ω в реальной почве. Выбранная комбинация контактных моделей будет обо- значаться как оптимизированная модель Герца-Миндлина JKR.

Параметры контактной модели Гер-ца-Миндлина JKR цифрового двойника почвенной среды [9, 10, 12] представлены в таблице 1.

Таблица 1 – Параметры контактной модели цифрового двойника почвенной среды Table 1 – Parameters of the contact model of the digital twin of the soil environment

№ п/п № item order	Параметры Parameters	Показатели Indicators
1	Модуль Юнга Е, МПа Young's module E, MPa	100
2	Коэффициент Пуассона ν Poisson's ratio v	0,3
3	Коэффициент статического трения почвы о почву f st Coefficient of static friction of soil against soil f st	0,9
4	Коэффициент динамического трения почвы о почву f d Dynamic friction coefficient of soil against soil f d	0,7
5	Диаметр частиц d, мм Particle diameter d, mm	5
6	Коэффициент статического трения f st.k Coefficient of static friction f st.k	0,3
7	Коэффициент динамического трения f d.k Dynamic friction coefficient f d.k	0,3

Стенки цилиндрической ёмкости Walls of a cylindrical container

Почвенные частицы Soil particles

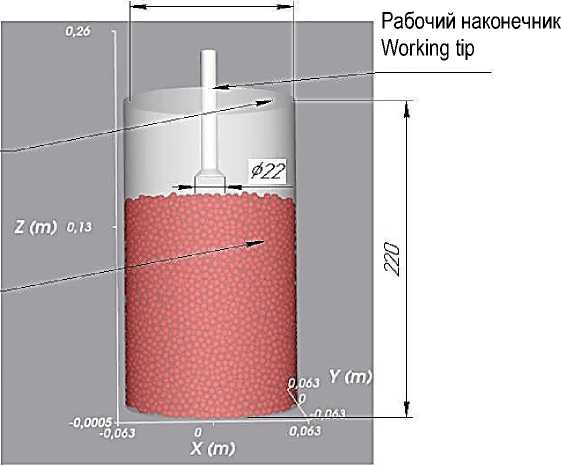
Рисунок 7 – Цифровой двойник для определения усилия пенетрации почвенных частиц Figure 7 – Digital twin for determining the penetration force of soil particles

Предварительно была создана трехмерная твердотельная модель цилиндрической емкости в программе Ком-пас-3D для проведения натурных экспериментов измерения усилия пенетрации по натурным размерам с высотой 220 мм, диаметром 125 мм и рабочий наконечник с диаметром 22 мм. Затем импортирована с разрешением «stl» в программный комплекс Rocky DEM. При моделировании установили скорость внедрения рабочего наконечника, равную 8 мм/с на глубину 80 мм. На рисунке 7 представлен цифровой двойник для определения усилия пенетрации почвенных частиц.

Разработанный цифровой двойник позволяет определять усилие пенетра-ции почвенных частиц в реальном времени.

Результаты исследования и их обсуждение. В таблице 2 представлены результаты натурных экспериментов измерения усилия пенетрации при изменении влажности почвы.

Таблица 2 – Усилие пенетрации почвы в зависимости от влажности Table 2 – Soil penetration force depending on humidity

Влажность ω, % Humidity ω, %	5,7	11,5	14,3	17,9	25,0
Среднее усилие пенетрации R z , н Average penetration force R z , n	172	117	71	78	92
Дисперсия Variance	63,5	15,5	28,5	72,5	67,5
Ср. квадр. откл. Wed. quad. dev.	7,97	3,94	5,34	8,51	8,22

Установлено, что при влажности 5,7% почва характеризуется плотной и твёрдой структурой, что приводит к высокому усилию пенетрации до 172 Н, так как частицы почвы плотно сцеплены, и для их раздвигания требуется значительное усилие. При этом с увеличением влажности до 11,5% усилие пенетрации снижается до 117 Н, так как влага действует как смазка между частицами почвы, уменьшая их сцепление. При этом почва становится более пластичной и легче поддаётся проникновению рабочего наконечника. При достижении оптимальной влажности в диапазоне от 14,3% до 25% наблюдается минимальное усилие пенетрации и постепенное увеличение до 92 Н. При повышении влаги почва становится переувлажнён-ной, теряет свою структуру и превращается в пластичную или даже текучую массу, а усилие пенетрации снова увеличивается, так как почва начинает вести себя как вязкая среда, оказывая большее сопротивление за счёт своей липкости и текучести.

На рисунке 8 представлен график изменения усилия пенетрации по результатам моделирования в программном комплексе RockyDEM.

Для обработки экспериментальных данных выбиралась стабильная стадия процесса пенетрации почвенных частиц. Результаты по определению усилия пе-нетрации почвенной среды от поверхностной энергии в цифровом двойнике представлены в таблице 3.

Для калибровочного теста по определению усилия пенетрации R z почвенной среды был проведено моделирование в диапазоне поверхностной энергии от 5 Дж/м² до 400 Дж/м².

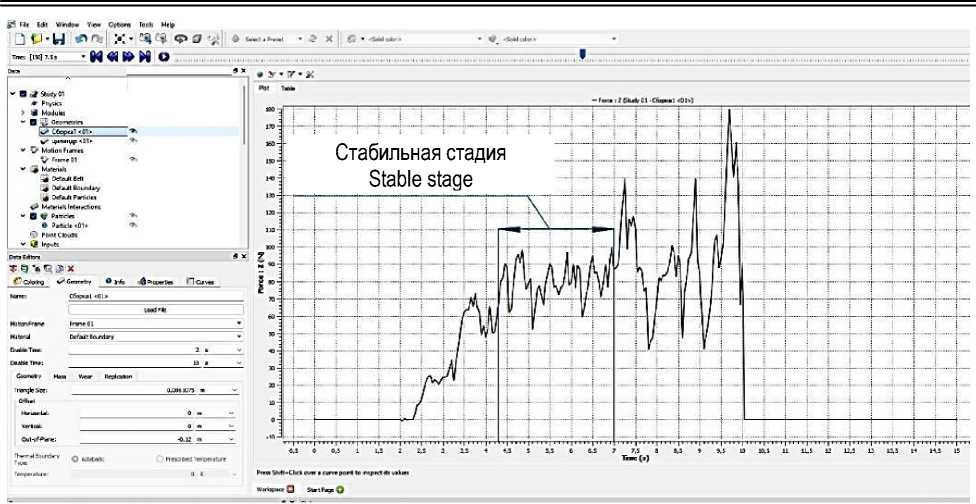
Рисунок 8 – График изменения усилия пенетрации по результатам моделирования в программном комплексе RockyDEM

Figure 8 – Graph of the change in the penetration force based on the simulation results in the RockyDEM software package

Таблица 3 – Изменение усилия пенетрации почвенной среды от поверхностной энергии в цифровом двойнике

Table 3 – Change in the penetration force of the soil medium from surface energy in a digital twin

Поверхностная энергия G s , Дж/м2 Surface energy G s , J/m2		Среднее усилие пенетрации R z , Н Average penetration force R z , n	Дисперсия Variance	Ср. квадр. откл. Wed. quad. dev.
5		5,29	5,29	1,10
10		8,59	3,33	1,82
15		4,5	1,49	1,22
20		7,12	1,58	1,25
25		8,69	2,38	1,54
50		24,98	24,06	4,9
75		39,46	40,04	6,32
100		52,9	116,85	10,8
120	Соответствует влажности 14–25% Corresponds to moisture of 14–25%	72,45	354,06	18,81
130		78,4	380,15	19,49
140		85,47	423,95	20,59
150		90,01	379,08	19,47
160		93,2	240,32	15,5
200		104,2	657,63	25,64
220		160,15	879,55	29,65
300		233,15	2045,52	45,22
400		266,77	1903,73	43,63

На рисунке 9 представлен график изменения усилия пенетрации от влажности почвы и от поверхностной энергии почвенных частиц.

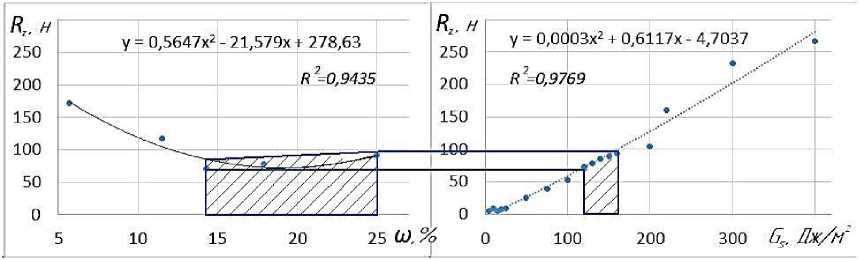
а a                                    б b а – от влажности почвы; б – от поверхностной энергии почвенных частиц Рисунок 9 – График изменения усилия пенетрации a – on soil moisture; b – on the surface energy of soil particles Figure 9 – Graph of the change in the penetration force

Таким образом, в результате натурных экспериментов установлено, что усилие пенетрации путем внедрения рабочего наконечника зависит от влажности почвы по полиноминальной зависимости (рисунок 9 а ): сначала уменьшается с увеличением влажности, достигая минимума при оптимальной влажности от 14% до 25%, а затем снова увеличивается при дальнейшем увлажнении. Полученные экспериментальные данные соответствуют результатам ранее проведенных исследований [12–14]. При меньшей и большей влажности обработка почвы не производится.

В результате обработки модельных экспериментов установлено, что измене- ние усилия пенетрации почвенной среды проходит по полиноминальной зависимости от 72,45 Н до 93,2 Н в зависимости от поверхностной энергии и соответствует натурным экспериментам при изменении влажности от 14 до 25%, что находится в диапазоне влажности физической спелости почвы.

По результатам сопоставления результатов натурных экспериментов по усилиям пенетрации в зависимости от влажности почвы (рисунок 10 а ) и в зависимости от поверхностной энергии по результатам моделирования (рисунок 10 б ) построена номограмма для выбора поверхностной энергии моделируемой почвенной среды.

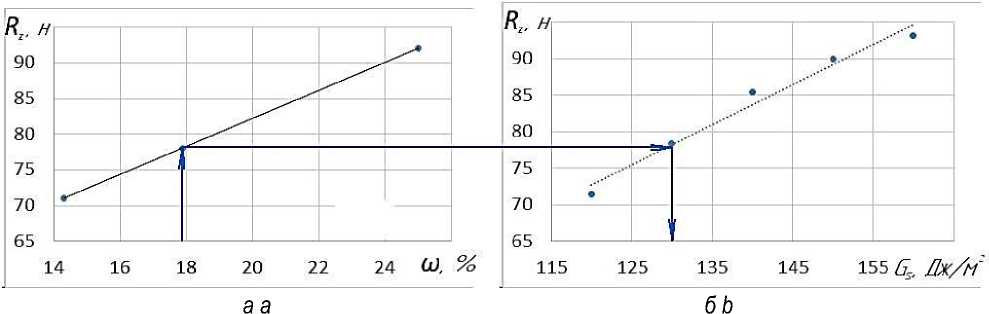
а – от влажности почвы; б – от поверхностной энергии почвенных частиц Рисунок 10 – Номограмма выбора значения поверхностной энергии моделируемой почвенной среды в зависимости от влажности реальной почвы a – on soil moisture; b – on the surface energy of soil particles

Figure 10 – Nomogram of the choice of the surface energy value of the simulated soil environment depending on the moisture of the real soil

Установлено, что изменение поверхностной энергии почвенных частиц в диапазоне от 120 Дж/м2 до 160 Дж/м2 (характеризующее изменение влажности) ведёт к увеличению усилия пене-трации от 72,45 Н до 93,2 Н. Данная область соответствует оптимальной влажности почвы от 14% до 25%.

Выводы. Результаты калибровки параметров контактной МДЭ-модели почвенной среды показали, что из выбранных параметров (модуль Юнга 100 МПа, коэффициент Пуассона 0,3, коэффициент статического трения 0,9, коэффициент динамического трения 0,7, диаметр частиц 5 мм) на характер изменения усилия пенетрации моделируемой почвенной среды значительно влияет поверхностная энергия. На основе проведенных модельных экспериментов была создана номограмма, позволяющая выбрать значение поверхностной энергии для моделируемой почвенной среды в зависимости от влажности реальной почвы. Эта номограмма предназначена для контактной модели Герца-Миндлина JKR, применяемой к чернозему с легкосуглинистым механическим составом. Полученные результаты калибровки по поверхностной энергии от 120 до 160 Дж/м² соответствуют оптимальной влажности почвы от 14% до 25%.

Полученные результаты необходимо применять при моделировании технологического процесса обработки почвы и разработки на их основе цифровых двойников почвообрабатывающих и посевных машин для прогнозирования энергетических и агротехнических показателей. По результатам проведенных исследований в перспективе планируется создание цифрового двойника почвенного канала с калибровкой физикомеханических свойств различных типов почвы по механическому составу.