Экспериментальная оценка связи энергии деформации с параметрами структурного состояния материала деформируемых поверхностей

Кинетическая термофлуктуационная концепция деформации и разрушения твердых тел [1,2], рассматривает энергию активации деформации U a.деф = U( о ,Т , у )= U ( ^ , Т<' '_:Х как функцию действующего напряжения σ , температуры Т и структурного состояния деформированного материала γ, характеризуемого уровнем накопленных повреждений . В статье рассмотрена связь удельной энергии деформации поверхностей испытываемых образцов с уровнем повреждаемости тонкой структуры материала приповерхностного слоя.

Методика испытаний

Испытывали торцевые поверхности цилиндрических образцов (диаметром 30 мм, высотой 18 мм) из стали 40Х, титанового сплава ВТ9 и бронзы БрАЖ 9-4 после точения, шлифования и притирки с алмазной пастой. Шероховатость поверхностей измеряли профилографом-профилометром ВИ-201, микротвердость - микротвердомером ПМТ-3 по ГОСТ 9450-76.

Энергию пластической деформации после механической обработки образцов оценивали методом склерометрии [3] на разработанном склерометре в процессе царапания обработанной поверхности алмазным индентором Виккерса с углом между гранями при вершине 1360.

Удельную энергию деформации рассчитывали по формуле  U деф = А деф /V деф , Дж/мм³ ,     (1)

где А деф =F τ∙ ∙L, работа деформации, Дж; F τ∙ ∙- тангенциальное усилие царапания (деформации), Н;

L - длина царапины, мм; V деф =S∙L- объем деформированного материала, мм³; S=0,07D² - площадь,

Карпухин Михаил Васильевич, аспирант, инженер НТЦ «Надежность поперечного сечения борозды при царапании, мм2; D – диагональ отпечатка индентора, мм. Для получения достоверных данных с доверительной вероятностью 0,95 проводили порядка 15 измерений.

Состояние тонкой кристаллической структуры поверхностных слоев оценивали методами рентгенографии после соответствующей механической обработки образцов. Оценивали изменения физического уширения рентгеновских интерференционных линий β, размеров блоков мозаик D и микроискажений ∆а/а, параметра решетки а (межатомного расстояния) и рентгенографической плотности дислокаций ρ.

Рентгенографирование деформируемых поверхностей проводили на дифрактометре Thermo Scientiffic в медном K α излучении при режиме работы трубки U =43 кВ, I =38 мА при скорости вращения фиксирующего счетчика (детектора ) 2 градуса в минуту. С каждого образца сначала снимали ди-фрактограмму для выбора интерференционных максимумов hkl после чего проводилось исследование состояния дефектной структуры по глубине поверхностного слоя методом скользящего пучка [4]. Съемки проводили при углах скольжения первичного пучка рентгеновских лучей α=2;5;10 градусов.

Разделение вклада отражения от малых областей когерентного рассеяния (блоков) и микроискажений в физическое уширение рентгеновских линий проводили методом гармонического анализа формы линии. Для практического определения коэффициентов разложения в ряд Фурье экспериментальной и эталонной кривых распределения интенсивности использовали специализированную программу для ЭВМ– WinRP 20-6 RC1. С помощью этого же про- граммного обеспечения меров блоков мозайк кажений Δа/а.

Рентгенографическую рассчитывали по формуле проводили расчеты раз-D и величины микроис-

плотность дислокаций ρ

О - 3/ ^Р = Dd ^г

.

Параметр решетки а (межатомное расстояние) находили с использованием программы XPowder.

Глубину проникновения h лучей в образец, или толщину материала участвующего в отражении рентгеновских лучей, определяли с учетом природы вещества, длины волны излучения, геометрии съемки и шероховатости поверхности.

Результаты испытаний

Дифрактограммы полученные со шлифованной поверхности, например, образца из стали 40Х, приведены на рис.1, а расчетные данные физического уширения для каждого максимума hkl - в табл.1.

Таблица 1. Результаты оценки физического уширения β (в градусах) интерференционных максимумов hkl в зависимости от угла скольжения α и глубины h проникновения рентгеновских лучей перед склерометрированием

№ образца	α, град	h, мкм	hkl 001	hkl 011	hkl 111	hkl 002
1	90	10…15	0,428	0,783	0,813	0,914
1	2	1,51	0,724	0,675	1,011	0,968
1	5	2,75	0,598	1,184	1,070	1,201
1	10	4,78	0,533	1,110	0,742	1,346

Результаты оценки изменений удельной энергии деформации по глубине деформированных поверхностных слоев образцов из указанных конструкционных материалов, подвергнутых обработке шлифованием, приведены на рис. 2.

Наибольшая энергия наблюдается у поверхности, что связано с высоким уровнем дефект-ности слоя h<3 мкм, уменьшение энергии по глубине может быть связано со снижением повреждаемости или, возможно, с ростом объёма деформируемого материала.

Рентгеноструктурные исследования изменения параметров тонкой кристаллической структуры по глубине деформированных поверхностных слоев шлифованных образцов (рис. 3.4.5), а также при различных видах механической обработки (рис. 6,

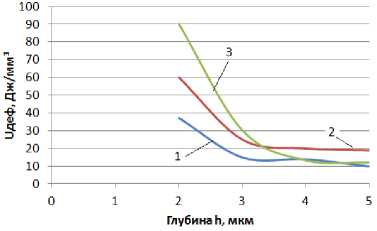
Рис. 2. Зависимость U деф от глубины внедрения индентора: 1- cталь 40Х, шлифование Ra=0,223 мкм, Н_µ=231; 2 - сплав ВТ 9, шлифование Ra=0,223 мкм,

Н µ =285.; 3 - бронзa БрАЖ9-4, шлифование Ra=0,223 мкм, Н µ =285.

7,8) показали их удовлетворительную корреляцию с изменениями удельной энергии деформации.

Как показали испытания, с увеличением глубины склерометрирования от поверхности энергия деформации U деф снижается по закону изменения плотности дислокаций ρ в материале поверхностного слоя.

В соответствии с дислокационной теорией прочности, развиваемой Коттрелом, Бейли, Хиршем и др., удельная энергия разрушения (деформации) определяется [5] при достижении в деформированном поверхностном слое критической плотности дислокаций ρ кр =10¹¹…10¹² см^-2 , как

А р ≈ U деф ≈ρ⋅∆ Q,                 (2)

а

б

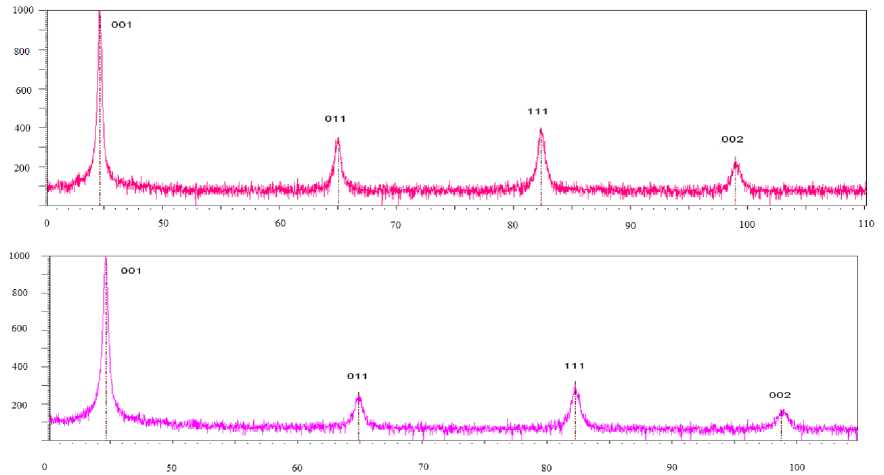
Рис. 1. Рентгеновские дифрактограммы с поверхностей: Образец №1, Сталь 40Х, шлифование, Ra=0,233 мкм: а) Дифрактограмма полученная методом скользящего пучка на глубину 1,51 мкм

Глу 6l IHi 111, мкм

(угол α=2 градуса); б) Дифра ктограмма полученная сканиров анием на глубину 10…15 мкм.

g I Ё

г

а

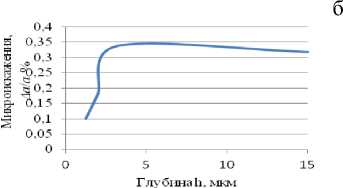
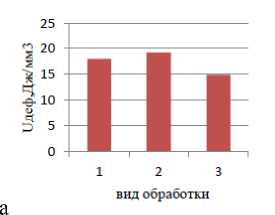
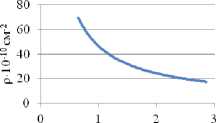
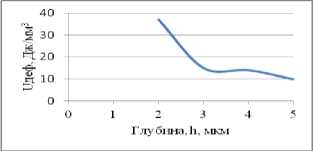
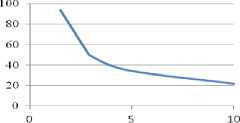
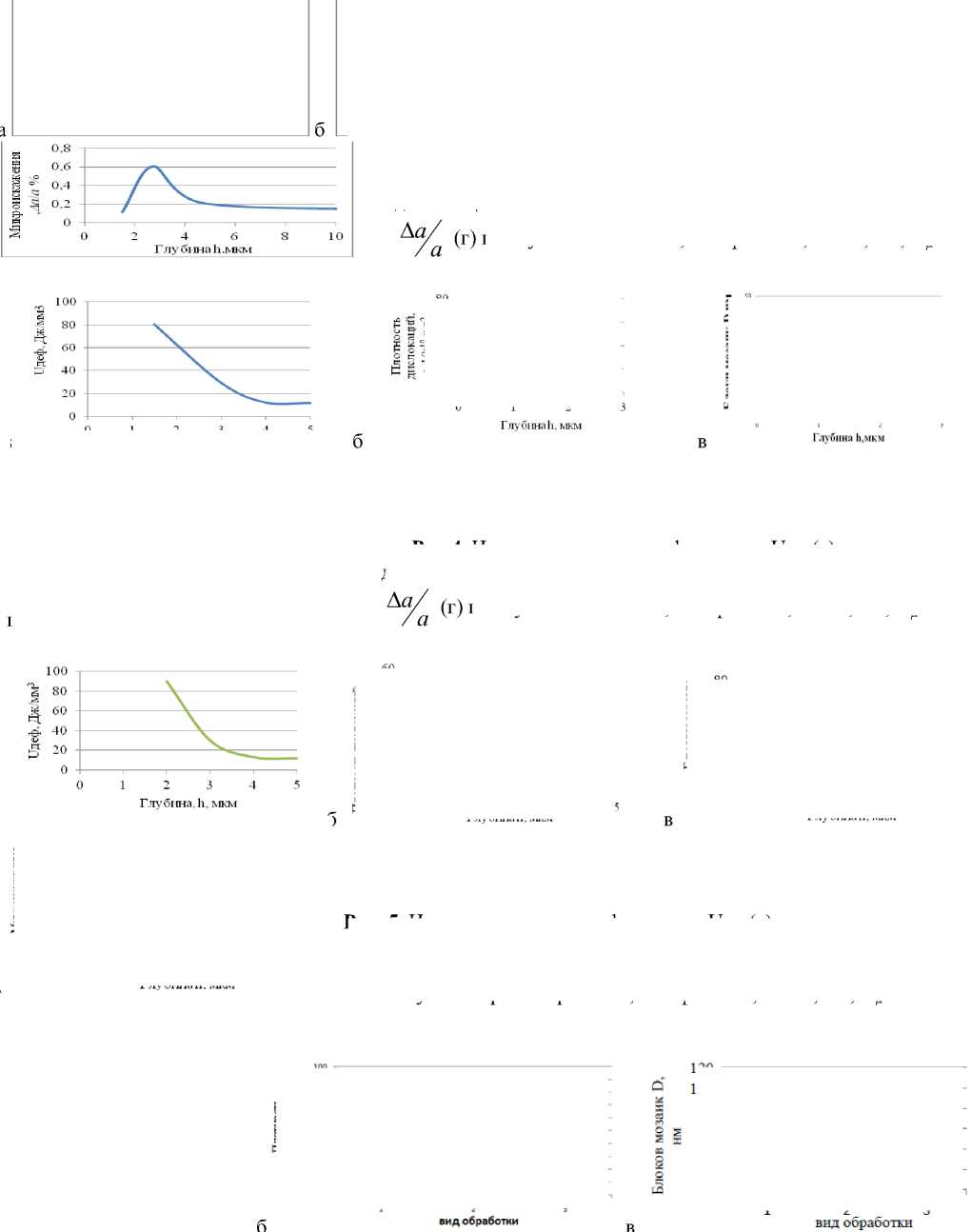
Рис.4. Изменение энергии деформации U деф (а), плотности дислокаций ρ (б), размеров блоков мозаик D (в), микроискажений по глубине:сплав ВТ9, шлифование, Ra =0,223, Н µ =285.

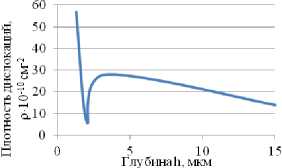
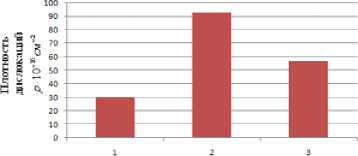
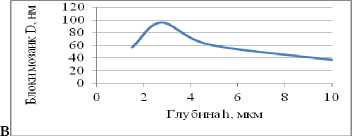
Рис. 3. Изменение энергии деформации U_де ф (а), плотности дислокаций ρ (б), размеров блоков мозаик D (в), микроискажений по глубине: сталь 40Х, шлифование, Ra =0,223, Н µ =231.

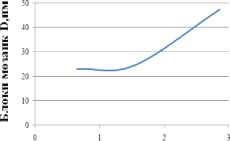
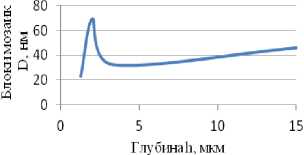
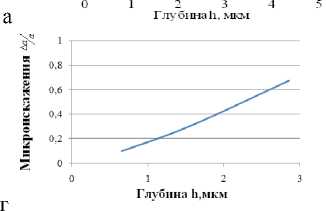
Рис. 5. Изменение энергии деформации Uдеф (а), плотности дислокаций ρ (б), размеров блоков мозаик D (в), микроискажений ∆a  (г) по глубине: бронза БрАЖ9-4, шлифование, Ra =0,223, Нµ=285.

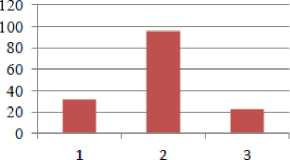
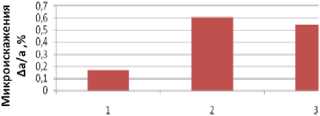
Рис.6. Зависимость энергии деформации U деф (а), плотности дислокаций ρ (б), размеров блоков мозаик D (в), микроискажений

∆ a  (г), от видов обработки стали 40Х: 1 - притирка,

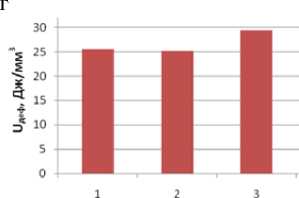
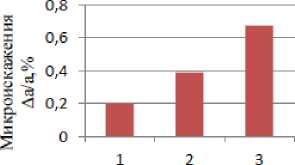
г

2 - шлифование, 3 – точение, глубина склерометрирования h≈3 мкм.

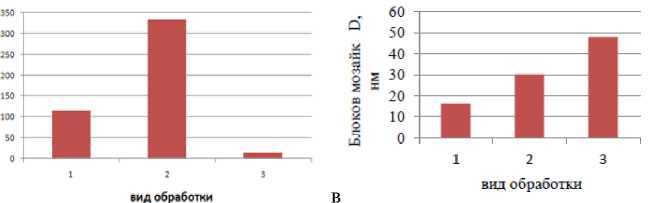
Рис.7. Зависимость энергии деформации U_де ф (а), плотности дислокаций ρ (б), размеров блоков мозаик D (в), микроискажений ∆ a  (г), от видов обработки сплава Вт9:

1 – притирка по шлифованию, 2-притирка по точению, 3 – шлифование, глубина склерометрирования h≈3 мкм.

а

бронзы БрАЖ9-4: 1 – притирка; 2 – шлифование тонкое, глубина склерометрирования h≈3 мкм.

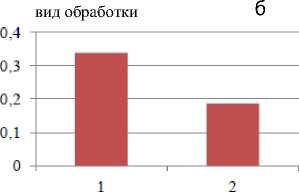
Вид обработки

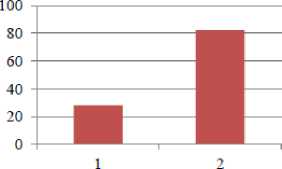
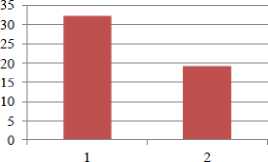
Рис.8. Зависимость энергии деформации U_де ф (а), плотности дислокаций ρ (б), размеров блоков мозаик D (в), микроискажений ∆ a  (г), от видов обработки

где А р – удельная энергия разрушения (деформации); ∆ Q – средняя энергия дислокаций на единицу длины, определяемая как

∆ Q= ρ⋅ G ⋅ в²/ (3(1-µ)), (3)

где в - вектор Бюргерса; µ- коэффициент Пуассона.

На основе выражений (2) и (3) получим расчетную формулу (4) накопленной энергии деформации U_де ф в зависимости от плотности дислокаций ρ деформированной структуры

U деф = ρ⋅ G ⋅ в²/ (3(1-µ)). (4)

Результаты оценки связи экспериментальных значений удельной энергии деформации с расчетными по формуле (4), полученными при различных значениях рентгенографической плотности дислокаций ρ по глубине поверхностного слоя сплава ВТ9 дефор- мированного при различных видах механической обработки, приведены в табл. 2 , при следующих исходных параметрах сплава [6]: модуль упругости Е=1,1⋅105 Н/мм2; модуль сдвига G=0,38⋅Е=0,418⋅105 Н/мм2; коэффициент Пуассона µ=0,34; вектор Бюргерса в=2,92⋅10-7 мм ∆Q=0,418⋅105(2,92⋅10-)2/

/(3(1-0,34))=1,8 ⋅ 10^-9 Дж/мм.

Анализ данных таблицы показывает, что экспериментальные значения U деф адекватно отражают уровень накопленных повреждений в материале. Экспериментальные значения изменяются в пределах от 16,6 до 59,5 Дж/мм³, расчётные от - 2,16 до 60,12 Дж/мм³.

Таблица 2. Расчётные и экспериментальные значения удельной энергии деформации U_де ф сплава ВТ по глубине при различных видах механической обработки

я я о о ю о св Я & X ю & О CD « О я § m	, 5 св X Й Я ЕЯ 2 >12" 2 в я U н О о о я	5 д । я § с£ § « §	Значения Uдеф, Дж/мм3
			расчёт ные	экспери-ментальные при h=3 мкм
Шлифование	0,65	5,685 ⋅ 109	10,23	29
	1,55	4,989 ⋅ 109	8,98
	2,86	1,316 ⋅ 109	2,37
Притирка после шлифования	0,65	2,170 ⋅ 109	3,906	59,5 (h=2 мкм)
	1,55	1,881 ⋅ 109	3,384	25,2
	2,86	1,144 ⋅ 1010	20,592	16,6 (h=5 мкм)
Притирка по точению	0,65	7,166 ⋅ 109	12,899	25
	1,55	1,204 ⋅ 109	2,16
	2,86	3,334 ⋅ 1010	60,12

Некоторое превышение экспериментальных значений над расчетными связано, очевидно, с дополнительным ростом плотности дефектов структуры перед алмазным индентором в процессе склеромет-рирования, а также с тем, что Uдеф≈Ар зависит не только от величины (скаляра) плотности дислокаций ρ, но и от энергии их взаимодействия друг с другом и с другими многочисленными дефектами деформированной структуры.

Выводы

Полученные методом склерометрии экспериментальные значения удельной энергии деформации поверхностных слоев образцов из разнородных конструкционных материалов после различных видов механической обработки адекватно отражают уровень и энергию накопленных повреждений тонкой структуры материала деформируемых поверхностей. Предложенное методическое решение оценки энергии активации пластической деформации пополнит арсенал методов испытаний рабочих поверхностей деталей машин и материалов в машиностроении.