Экспериментальная верификация частотного метода оценки осевой нагрузки и несовершенства граничных условий в арматурных стержнях

ВЕСТНИК ПНИПУ. МЕХАНИКА № 3, 2024PNRPU MECHANICS BULLETIN

Оценка усилий и жесткостей соединений имеет существенное значение при определении остаточного ресурса железобетонных конструкций мостов, предварительно напряженных арматурными стержнями и канатами, анкерного крепления кровли подземных горных выработок, стяжных стержней, обеспечивающих целостность конструкций исторических зданий, и в других конструкциях. В литературе описан ряд методов оценки осевой нагрузки и качества заделки стержней [1–18]. Они могут быть сгруппированы по статическому и динамическому признакам, исходя из характера лежащих в их основе механических взаимосвязей и последующих измерений. Статические методы требуют измерения деформации под действием статической силы для оценки осевой нагрузки в стержне [1–6]. Один из них основан на определении усилия вытягивания анкера [3]. Этот метод применительно к горным выработкам является трудоемким и небезопасным для персонала. Чаще проводятся испытания на изгиб под действием заданной поперечной силы [1; 4; 5]. С позиции эксплуатации недостатками статических методов являются: необходимость подвешивать к стержневым элементам значительный вес, трудности измерения малых деформаций или перемещений с необходимой точностью [5] и в целом время и оказываемое влияние на работу конструкции. Динамические методы, с другой сто- роны, требуют идентификации вибрационных характеристик стержня либо только по собственным частотам, либо по частотам вместе с соответствующими собственными формами. Наиболее распространенный частотный метод основан на зависимости между напряжением в арматуре и частотой ее собственных поперечных колебаний, которые устанавливаются в натянутой арматуре через определенное время после выведения ее из состояния равновесия ударом или каким-либо другим воздействием. Качество заделки стержневых элементов оценивается также по уровню добротности послеударных затухающих колебаний [3]. Ввиду важности определения продольных усилий в арматуре статические и динамические методы стандартизованы [6], выпущены приборы, реализующие эти методы.

В последнее время в литературе появляется все больше исследований, посвященных развитию динамических подходов к определению продольных усилий в стяжных стержнях не только по одной, но и по нескольким характерным собственным частотам [7–17]; некоторые из подходов требуют определения модальных форм [12–15]; для этого, в частности, используются дополнительные массы, сравнение с результатами МКЭ и оптимизация на основе генетических алгоритмов [7]. Актуальным вопросом является влияние граничных условий на концах стяжных стержней на динамические характеристики, в том числе на частоты свободных колебаний. В этом плане рассматриваются заделки не только в виде пружинных шарниров с неизвестными линейными и угловыми жесткостями [7–18], но и как Винклеровские основания с неизвестными коэффициентами постели [9; 10].

Перечисленные и ряд других работ посвящены, как правило, анализу измерений на реальных объектах со стяжными стержнями, имеющими многократное превышение свободной длины по сравнению с габаритами поперечного сечения. Естественной моделью для описания изгиба и поперечных колебаний таких стержней является модель Эйлера – Бернулли. В настоящей работе использована более общая модель колебаний стержня на основе балки Тимошенко, которая подходит для стяжных стержней с более широким диапазоном отношения длины к габаритам поперечного сечения. При определении осевой нагрузки и коэффициентов жесткости заделки стержня использовался, как и в [17; 19], алгоритм basin-hopping – стохастический алгоритм, с помощью которого находится глобальный минимум гладкой скалярной функции одной или нескольких переменных. Проведена экспериментальная верификация динамической методики на стержневых моделях с известными значениями продольного усилия и угловой жёсткости заделки. Для этого в качестве модельных образцов рассмотрены две балки. В одной из них при растяжении в испытательной машине создавались заданные продольные усилия. Другая балка имела вид консоли с торцевым резьбовым креплением, по степени затяжки которого, контролируемой по статическому прогибу свободного конца консоли, определялся коэффициент угловой жёсткости крепления.

Теоретические модели

где x ( z , t ) – поперечное смещение центра тяжести сечения, θ( z , t ) – угол поворота поперечного сечения, α – коэффициент, учитывающий неравномерность касательных напряжений по сечению, зависящий от формы сечения, E – модуль упругости, G – модуль сдвига, I – момент инерции сечения в плоскости изгиба, F – площадь поперечного сечения, ρ – плотность материала.

Граничные условия для балки с упругими связями – пружинными шарнирами с угловыми жесткостями с 0 , с l :

x

= ⁰, c 0 ⁰I z = 0 = ^EI I⁰

d .z

Полагая

z = 0

, c i ⁰

d0

— El--

d z

z = l

{x (z, t), 0( z, t)} = {X (z), ©( z )} exp (iat)

и исключая угол поворота θ из системы уравнений (1), приходим к разрешающему уравнению относительно функции поперечного смещения оси балки:

„ ,V Ip»2 I (aE + G) — GN)F + a N2X +--X +

EGFI                    (3)

pm2 (a(I»2p + N) — GF)

---^------------'- X = 0. EGI

С учетом того, что для подобных балок критическая частота ω c колебаний по модели Тимошенко, определяемая из равенства:

® с

GF N

^^^^^^^^^^^^^^^^^^^^^^^^ ^^^™ ^^^^^^^^^^^^^^^

a Ip  Ip ’

Рассмотрим поперечные колебания балки, нагруженной заранее неизвестной продольной силой при неизвестных угловых жёсткостях закреплений. Расчётная схема такой балки представлена на рис. 1.

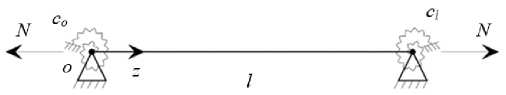
Рис. 1. Расчётная схема балки длиной l с продольной нагрузкой N и угловыми упругими закреплениями концов с жесткостями с 0 , с 1

Fig. 1. Design scheme of a beam of length l with longitudinal load

N and angular elastic bracing of the ends with stiffnesses с 0 , с 1

Для описания свободных поперечных колебаний балки используем модель колебаний балки Тимошенко с учетом продольного усилия [20] в обозначениях [21]:

d2Q_p_d2Q- gff1_aNYq-—1

5 z ² E d t ² = a EI I GF Y 3 z ) ,

d2x ap d2x _^i aN^50 dz ~g~дё4 -gfJaz, лежит значительно выше верхней границы акустического спектра, решение уравнения (3) может быть представлено в виде:

X ( z ) = С 1 cos X z + С ₂ sin X z + С 3 ch p z + С 4 sh p z , (4)

0 ( z ) = С sin X z | ^aP®- — X | + С cos X z | X —^aP®- | +

^{W 1} I G X J ² I      G X )

I ap® 1           I ap® 1

+ С sh p z p +-- + С ch p z p +--,

3 I    G p J 4     ^    G p J где

X =

I ( рш ² 1 ( aE + G ) - GN ) F + aN ²    | ( рш ² 1 ( a E + G ) - GN ) F + a N ² Y pm ² ( a ( I m ² p + N ) — GF )

2 EGFI            vl            2 EGFI I EGl

( pm² 1 ( a E + G ) - GN ) F + a N ²    | ( рш² 1 ( a E + G ) - GN ) F + a N ² 1 pm² ( a ( I m²p + N ) - GF )

EI ^ _ EI gp.¹

„ у c ^ap . c x

0 X G

. ei ц - EI ^apm 2 G

cos X l

sin X l

( ap. l X G

- X l C i sin X l +

, ap. 1

X-        c, cos X l +

X G J

₊ [^2 -X ² I G

l EI cos X l

ap.

A G

-X ² l EI sin X l

ch ц l ape 1 ц +------ c, sh цl + l ц G J ap. 1

+ 1ц ² + G— l EI ch Ц l

c ap.

C»ц + ц G sh ц l f , ap.1      .

| ц+—— l cl ch цl+ l    ц G J f 2 ap.21       .

+ 1ц + — g — l El sh ц l

Для модели балки Эйлера – Бернулли параметры λ, μ принимают вид:

X =

N f \     ® ² p F

-    +        +

2 El \l 2 El J     El

ц =

N f N Y ® ² p F ^{+          4}

\ 2 El 1 2 2 El J El

Граничные условия для стержня с неизвестными угловыми жесткостями по этой модели:

x|     = 0, c₀ —

¹ z = 0 ^{l          0} a z

z = 0

= El ^ 5 z ²

z = 0

5x

, c

l dz

= - El ^ 5 z ²

.

Соответствующее частотное уравнение:

1	0	1	0
El X 2	C 0 X	- El ц 2	c 0 ц
cos X l	sin X l	ch ц l	sh ц l
cl X sin X l -	cl X cos X l -	cl ц sh ц l +	cl ц ch ц l +
El X 2 cos X l	- El X 2 sin X l	+ EI ц 2 ch ц l	+ EI ц 2 sh ц l

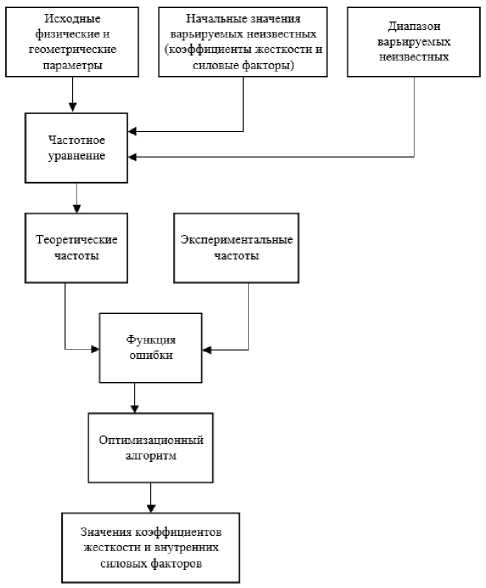
Рис. 2. Оценка коэффициентов угловой жесткости заделки и продольной силы по собственным частотам: блок-схема алгоритма

Fig. 2. Estimation of angular stiffness and longitudinal force coefficients from natural frequencies: algorithm block diagram

При заданных параметрах балки, действующей продольной силе и жесткостях заделки выписанные частотные уравнения обеспечивают однозначное определение собственных частот, соответствующих определённым формам колебаний балки. В то же время решение обратной задачи, исходя из известных собственных частот балки, может быть неоднозначным. Для поиска значений угловых жесткостей заделок с 0 , с 1 и усилия N в модели балки Тимошенко были применены алгоритмы глобальной оптимизации (basin-hopping) и локальной оптимизации – метод Нелдера – Мида подобно тому, как это реализовано в [8; 17; 19] на модели балки Эйлера – Бернулли. Метод является итеративным, каждый цикл которого состоит из случайного возмущения координат, локальной минимизации, принятия или отбрасывания новых координат на основе минимального значения функции. Краткое изложение алгоритма содержится в приложении. На рис. 2 показана блок-схема, обобщающая принятый метод.

Оценка производится по минимуму функции ошибок, называемой квадратичной функцией потерь [22], при сравнении теоретических и экспериментальных частот:

N

A = N Z (f^-- f ,i)2, (5)

где f exp,i – i -я экспериментальная частота, f th,i – i -я теоретическая частота, а N ограничено снизу числом искомых неизвестных при решении обратной задачи.

Преимуществом применения квадратичной функции потерь (5) является инвариантность к знаку: значение функции всегда положительно, т.е. происходит объективное накопление ошибки от каждого из слагаемых, в то время как при использовании линейной функции, как в [17], возможна ситуация, когда большую положительную ошибку от первого слагаемого «погашает» большая отрицательная ошибка от второго.

Для выделения в качестве главного неизвестного угловой жёсткости крепления стержня, наряду с общей расчетной схемой, изображенной на рис. 1, рассмотрим поперечные колебания консольной балки с неизвестной угловой жёсткостью закрепления. Расчётная схема такой балки представлена на рис. 3.

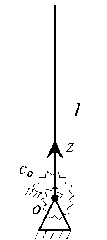
Рис. 3. Расчётная схема балки длиной l с упругим угловым закреплением конца с жесткостью с 0

Fig. 3. Design scheme of a beam of length l with elastic angular fixing of the end with stiffness c 0

Граничные условия для консольного стержня с упругим узлом по модели Тимошенко:

x

I z = 0

= 0, c 0 0|

I z = 0

= EI ™ d z

z = 0

5z

= 0,

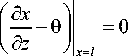
Соответствующее частотное уравнение примет вид:

EI X 2 - EIOP^L

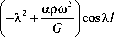
ap®² sin X l

X G

, c 0 “P“ 2 c X--

⁰     X G

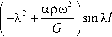
ap®² cos X l X G

- EI p 2 - EI ^ap ® 2

G

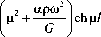
ap®² sh p l p G

c 0P + c 0ap®2 p G

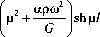
ap®² ch p l p G

Граничные условия для консольного стержня с угловой жёсткостью в закреплении по модели Эйлера – Бернулли:

x

z = 0

= °, c 0 ? d z

z = 0

= EI ^

5 z ²

z = 0

d ² x = 0 5 3 x

az2 ~ ’ az2

z = l

Частотное уравнение в этом случае может быть записано в виде равенства нулю определителя:

1	0	1	0
EI X 2	c 0 X	- EI p 2	c 0 p
-X 2 cos X l	-X 2 sin X l	p 2 ch p l	p 2 sh p l
X 3 sin X l	-X 3 cos X l	p 3 sh p l	p 3 ch p l

= 0.

Полученные из приведенных уравнений значения частот сравниваются ниже с экспериментально найденными частотами растянутого и консольного стержней.

Экспериментальная верификация теоретических моделей

Предметом экспериментального изучения были послеударные поперечные колебания стальной полосы 1 (рис. 4, а ), закрепленной в разрывной машине МИМ.2 двумя механическими клиновыми захватами 2 , имитирующими упругие заделки, при малом и значительном статическом растяжении силами, равными 0,15 и 1,97 кН. Длина полосы между захватами l = 0,585 м, поперечное сечение: 2 на 48 мм. Для балки, рассматриваемой в эксперименте, условия закрепления обоих концов одинаковы; поэтому можно считать с 0 = с l = с.

Колебания в плоскости наименьшей жесткости возбуждались ударом металлического шарика по широкой грани в двух местах: посередине длины полосы и на четверти длины, чтобы обеспечить возбуждение как симметричных, так и антисимметричных форм. С противоположной от места удара стороне полосы располагался лабораторный микрофон 3 (см. рис. 4, а ), соединённый со спектроанализатором типа A19-U2, данные из которого поступали в ЭВМ.

Также экспериментально изучался спектр поперечных колебаний консольного дюралюминиевого цилиндрического стержня длиной l = 0,745 м с диаметром d = 24,7 мм при различной величине затяжки резьбовой шпильки на конце стержня 1 (см. рис. 4, b , c ) в массивный стальной стол 2 со шлифованной поверхностью в месте контакта. Для статического измерения величины угловой жесткости заделки консоли при помощи датчика перемещения 3 типа ЛИР-14 определялся прогиб её конца под действием гирьки 4 массой 200 г .

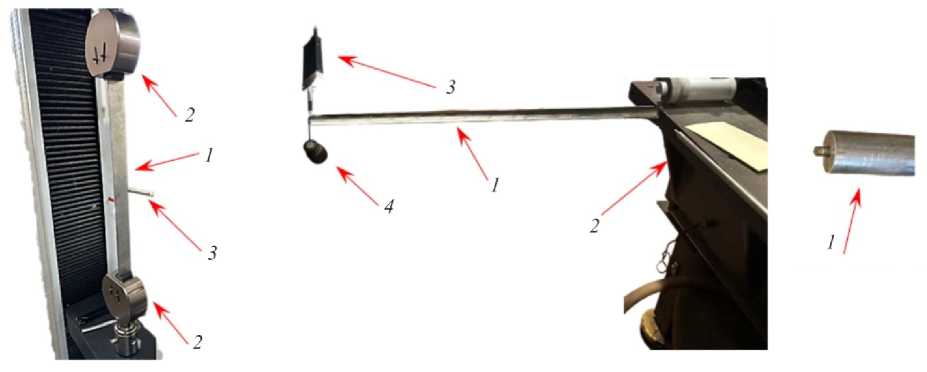
а                                                 b                                         c

Рис. 4. Экспериментальная установка для статического и динамического определения продольной силы ( а ) и угловой жёсткости крепления ( b ) образцов; резьбовая шпилька для ввинчивания консоли в массивный стол ( c )

Fig. 4. Experimental setup for static and dynamic determination of longitudinal force ( a ) and angular stiffness of fixing ( b ) of specimens; threaded rod for screwing the cantilever into a solid table ( c )

На рис. 5, 6 приведены фрагменты спектров колебаний экспериментальных образцов в акустическом диапазоне: на рис. 5 – спектры полосы при растяжении силами 0,15 кН ( а ) и 1,97 кН ( b ), а на рис. 6 – спектры консоли при максимально возможной ( а ) и слегка ослабленной ( b ) затяжке резьбового крепления.

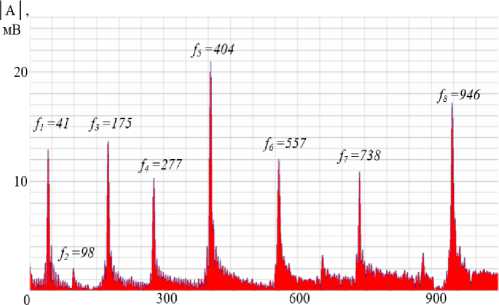
Частота, Гц

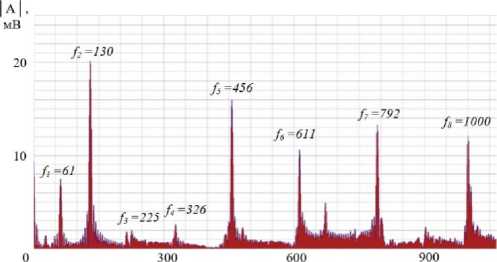
Частота, Гц

b

Рис. 5. Экспериментальные акустические спектры полосы при растяжении силой 0,15 кН ( а ) и 1,97 кН ( b )

• Fig. 5.    Experimental acoustic spectrum of the strip under tension with a force of 0.15 kN ( a ) and 1.97 kN ( b )

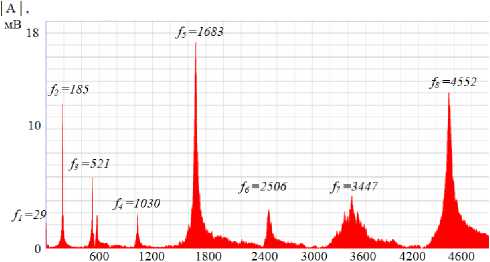
Частота, Гц

а

Частота, Гц

b

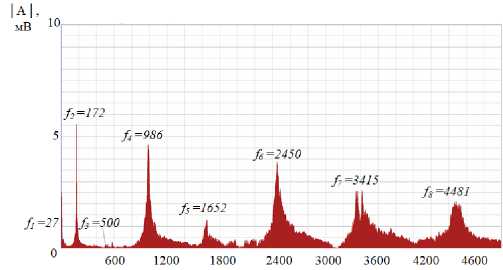
Рис. 6. Экспериментальные акустические спектры консольного стержня при максимальной ( а ) и слегка ослабленной затяжке ( b )

• Fig. 6.    Experimental acoustic spectrum of a cantilever rod at maximum ( a ) and slightly loosened tightening ( b )

Таблица 1

Экспериментальные собственные частоты тонкостенной полосы при малой ( f ^{( A )} i ) и значительной ( f ^{( B )} i ) растягивающей силе в Гц

Table 1

Experimental natural frequencies of a thin-walled strip at small ( f ^{( A )} i ) and large ( f ^{( B )} i ) tensile force in Hz

i	1	2	3	4	5	6	7	8
f ( A ) i	41	98	175	277	404	557	738	946
f ( B ) i	61	130	225	326	456	611	792	1000

При сопоставлении результатов, полученных по различным расчётным моделям, можно отметить, что для данной тонкостенной полосы при возбуждении колебаний в плоскости наименьшей жесткости учет сдвиговой деформации и инерции вращения не дает принципиальных отличий в определении растягивающей силы, чего нельзя сказать о результатах для второго экспериментального образца – консольного цилиндрического стержня, используемого при тестировании методики определения угловой жесткости упругого узла.

Определение величины продольной силы и коэффициентов угловой жесткости зажимов тонкостенной полосы по экспериментальным частотам производилось с помощью описанного выше стохастического метода. Границы поиска продольной силы были взяты от 0 до 4000 Н, начальное приближение задавалось в 1800 Н. Результаты расчётов с использованием одной первой, двух,…, восьми собственных частот представлены в виде диаграммы на рис. 7. Видно, что с приемлемой погрешностью менее 2 % (1950 Н против 1970 Н в статике) продольная сила определяется при учёте не более чем пяти первых собственных частот поперечных колебаний стержня, что важно при анализе спектров, зашумленных паразитными частотами. Следует также отметить, что коэффициент угловой жесткости захватов при последовательном увеличении верхней границы поиска в диапазоне от 0 до 100 000 Нм/рад каждый раз достигал верхней границы заданного диапазона, что указывает на допустимость считать захваты жесткими заделками.

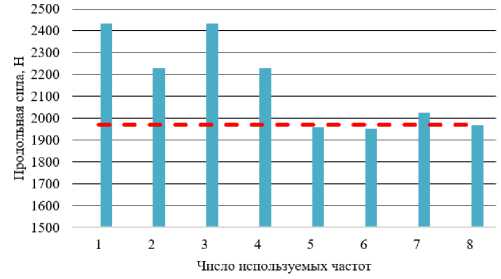
Рис. 7. Значения продольной силы, определённые динамическим методом по одной первой, двум, … восьми собственным частотам; штриховой линией показано значение продольной силы, заданное в растягивающей установке

• Fig. 7.    Longitudinal force values determined by the dynamic method using one first, two, ... eight natural frequencies; the dashed line shows the value of the longitudinal force set in the tensile rig

В случае консольного стержня угловая жесткость упругого узла является основной неизвестной. В табл. 2 приведены восемь первых собственных частот дюралюминиевого цилиндрического консольного стержня при различной величине угловой жесткости упругого узла до и после незначительного ослабления затяжки.

Таблица 2

Собственные частоты консольного стального стержня до ( f ^{( С )} i ) и после ( f ^{( D )} i ) ослабления затяжки в Гц

Table 2

Natural frequencies of the cantilever steel rod at maximum ( f ^{( С )} i ) and and slightly loosened ( f ^{( D )} i ) tightening in Hz

i	1	2	3	4	5	6	7	8
f ( C ) i	29	185	521	1030	1683	2506	3447	4552
f ( D ) i	27	172	500	986	1652	2450	3415	4481

По графикам амплитудно-частотных зависимостей рис. 6 и данным табл. 2 видно, что ослабление величины затяжки приводит к снижению собственных частот консоли, что позволяет использовать это снижение при решении обратной задачи определения угловой жесткости заделки; при этом учитывается преобладающее влияние на частоту поперечных колебаний угловой жёсткости в сравнении с линейной жёсткостью заделки [2]. Используя стохастический метод минимизации функции потерь по аналогии с рассмотренным выше растянутым образцом, для измеренных независимо механических свойств материала консоли ( Е = 72 ГПа, ρ = 2780 кг/м ³ ) по первым четырем собственным частотам ввинченного до упора консольного стержня получены следующие коэффициенты угловой жесткости по модели Тимошенко и Эйлера – Бернулли соответственно: 56 590, 47 600 Нм/рад. Границы поиска угловой жесткости заделки были приняты от 40 000 до 60 000 Нм/рад, начальное значение – 50 000 Нм/рад. Сопоставляя с результатом, полученным статическим методом ( c = 55 500 Нм/рад), можно утверждать о заниженном более чем 10 % значении коэффициента жесткости, полученном по модели Эйлера-Бернулли, тогда как при использовании модели Тимошенко отличие от эксперимента составляет менее 2 %. Коэффициент угловой жесткости заделки после незначительного ослабления резьбовой затяжки консоли, определённый через набор экспериментально зарегистрированных частот, составил 21 550 Нм/рад, тогда как по статическим измерениям – 20 790 Нм/рад. Различие здесь составило менее 4 %. Как видно из этих и других сопоставлений, не включённых в статью, рассмотренный метод определения жесткостей заделки достаточно чувствительный и точный; отличия в частотах собственных колебаний консоли, не превышающие 7 %, позволяют определить резкое снижение угловой жёсткости заделки (в приведенном примере – в 2,6 раза).

Заключение

Представлены некоторые результаты сопоставлений расчётных значений продольных усилий и величин угловой жесткости заделки упругих стержней, определенных по спектру послеударных колебаний с использованием алгоритма basin-hopping, основанного на минимизации методом Монте-Карло, с экспериментальными результатами прямых измерений этих величин. Для выделения главного вклада каждой из измеряемых величин измерения и расчёты проводились отдельно на моделях и образцах стержня, растягиваемого в испытательной установке, и на консольном стержне при разной величине затяжки резьбового крепления консоли. По полученным результатам измерений можно судить о достаточно высокой согласованности теоретических и экспериментальных результатов. Так, при определении величины растягивающего усилия расхождение между теоретическим и экспериментальным значениями не превысило 2 %. Также теоретически показана зависимость критической частоты Тимошенко от внутреннего силового фактора – растягивающей силы.

По результатам, полученным при определении коэффициента угловой жесткости крепления при различной величине затяжки цилиндрического консольного стержня, можно сделать вывод, что даже незначительные изменения спектра могут быть использованы для выявления степени неидеальности граничных условий. Так, при определении коэффициента угловой жесткости заделки консоли для принятых механических свойств образца при отличиях в первых нескольких теоретических и экспериментальных частот менее 10 % от случая с максимальной затяжкой, коэффициент жесткости заделки получен отличающимся более чем в два раза. При этом, как и следовало ожидать, определение величин продольной силы и жесткости заделки динамическим методом у стержней средней длины намного лучше со- гласуется со значениями, определенными статическим методом, при использовании модели Тимошенко, чем по модели Эйлера – Бернулли. Данный результат может быть использован, например, при обследовании пред-напряжённых канатов мостовых переходов с целью выявления реальных продольных усилий в растянутых канатах, по сравнению с проектными; для этого обычно выполняется вскрытие бетонной одежды ездового полотна до обнажения канатов на длине от 1,7 до 20 м при диаметре каната 32 мм [1]. Такое протяжённое вскрытие выполняется для обеспечения адекватности результатов расчёта продольного усилия по динамическому методу с использованием стержневой модели Эйлера – Бернулли. При использовании стержневой модели Тимошенко длину высвобождаемой части канатов, как следует из результатов данной работы, можно значительно сократить без уменьшения точности получаемых результатов.