Экспериментальная верификация моделей деформационного поведения и высокоскоростного разрушения титанового сплава ВТ6

Для обеспечения стойкости лопаток вентилятора авиационного газотурбинного двигателя (ГТД) к эксплуатационным повреждениям проводится исследование процессов соударения лопатки с разнообразными посторонними предметами (льдом, птицами, твердыми предметами с взлетно-посадочной полосы). Математическое моделирование повреждения лопатки при соударении представляет собой решение нестационарной динамической контактной задачи механики деформируемого твердого тела. Необходимым условием моделирования является наличие верифицированной модели деформационного поведения и разрушения материалов лопатки и повреждающего предмета при высоких скоростях деформации.

Цель настоящего исследования: верификация и идентификация моделей деформационного поведения и высокоскоростного разрушения титанового сплава ВТ6 при скоростях деформации, соответствующих условиям эксплуатационного повреждения лопаток вентилятора ГТД.

В задачах высокоскоростного соударения модель материала должна описывать упругопластическую деформацию и разрушение при соответствующей условиям скорости деформации – до 106 с-1 [1]. Для описания поведения материалов при высоких скоростях деформирования существует ряд математических моделей разной степени сложности, различающиеся как кругом учитываемых факторов, так и количеством подлежащих экспериментальному определению параметров [2]. В настоящей работе рассмотрены две наиболее часто используемые при описании процессов высокоскоростного соударения модели поведения материала: Купера-Саймондса (Cowper-Symonds) [2] и Джонсона-Кука (Johnson-Cook) [3]. Параметров этих моделей для исследуемого сплава ВТ6 в литературных источниках найти не удалось. В работе [4] необходимые параметры приведены для аналога материала ВТ6 – титанового сплава Ti-6Al-4V, имеющего имеют близкий химический состав и механические свойства [5-7].

Первым этапом исследования было проведение эксперимента по высокоскоростному повреждению в условиях, близких к реальному повреждению лопатки вентилятора посторонним предметом. Задачей данного этапа было получение результатов, пригодных для верификации и идентификации математических моделей поведения сплава ВТ6. В качестве модельной задачи, реализуемой в эксперименте, а затем в расчетах, выбрана задача о соударении стального шара с пластиной из исследуемого материала. Экспериментальный образец представляет собой плоскую прямоугольную пластину размером 75х200 мм и толщиной 1,01 мм из сплава ВТ6. Повреждающим предметом является стальной шар диаметром D=10 мм. В эксперименте исследуемый процесс соударения реализован в следующей постановке: пластина-образец жестко закреплена на высоте 20 мм от основания (консольная часть 75х180 мм), повреждающий предмет (шар) движется со скоростью V=400 м/с в направлении средней линии пластины перпендикулярно к ее поверхности; вектор скорости шара проходит через его центр и среднюю линию пластины и расположен на высоте от места закрепления образца h=40 мм (рис. 1). Параметрами для идентификации и верификации математических моделей поведения материала являются геометрические характеристики полученного в эксперименте повреждения и величина предельной деформации образца в зоне разрушения.

Экспериментальное исследование проводились на специальной установке на базе газовой пушки (рис. 2). Установка состоит из газовой пушки (поз. 1), устройства крепления и позиционирования (поз. 4) исследуемого образца (поз. 3). Они смонтированы на жестком массивном основании (поз. 6). Для определения скорости повреждающего предмета используется электронный измеритель скорости ИБХ-716 (поз.2). Для регистрации параметров движения повреждающего предмета после соударения в зоне исследования устанавливается экран-уловитель (поз. 5). Для определения остаточных деформаций на образец в месте предполагаемого повреждения с лицевой и тыльной сторон специальной краской нанесена сетка с шагом 1 мм (рис. 3). Остаточные деформации материала образца в зоне повреждения определялись по искажению ячеек сетки.

Рис. 2. Экспериментальная установка:

1 – газовая пушка; 2 – электронный измеритель скорости повреждающего предмета; 3 – исследуемый образец; 4 – устройство крепления и позиционирования; 5 – экран-уловитель; 6 – основание

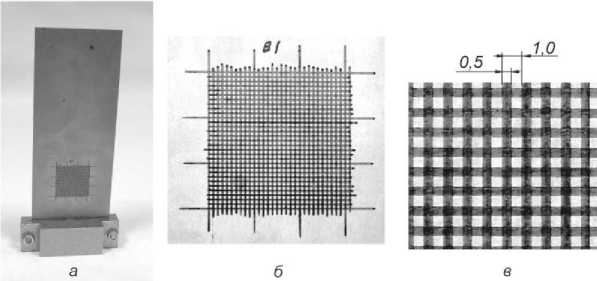
Рис. 3. Пример образца, подготовленного к экспериментальным исследованиям:

а – исследуемый образец; б – делительная сетка в зоне предполагаемого повреждения; в – увеличенный фрагмент делительной сетки

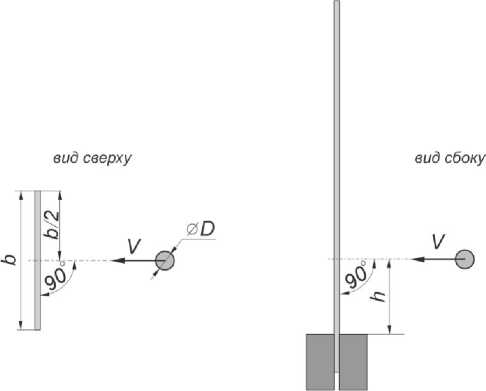
Рис. 1. Параметры схемы экспериментального моделирования соударения

Замеренное в эксперименте значение скорости повреждающего предмета составило 399 м/с. В результате соударения на образце образовалось повреждение в виде сквозного отверстия диаметром 8,25 мм с отгибом в сторону движения шара и наружным диаметром отогнутой части с тыльной стороны 9,5 мм (рис. 4). Радиус сопряжения, образовавшегося при отгибе, 3 мм. Глубина образовавшейся лунки составила до 5,7 мм. На границе сквозного отверстия образовались множественные разрывы преимущественно радиального (по отношению к отверстию) направления. Кроме того, образовалось пять магистральных тещин преимущественно радиального направления длиной 6,1-10,25 мм. В результате разрушения произошло отделение крупного фрагмента («пробка»). Он имеет чашевидную форму с радиусом вогнутой сферической поверхности около 5 мм. Форма отделившегося фрагмента близка к кругу диаметром 6,8-7 мм. Поверхность разрушения – коническая с вершиной со стороны выпуклой поверхности «пробки». Вогнутая поверхность отделившегося фрагмента гладкая без видимых повреждений. На выпуклой поверхности имеются множественные разрывы преимущественно окружного направления. Векторы скорости повреждающего предмета и «пробки» после соударения совпадают по направлению с вектором скорости повреждающего предмета до момента соударения. Распределение интенсивности деформаций εi, определенной методом делительных сеток, симметрично относительно центра отверстия, Максимальная интенсивность деформации εi составила 0,4.

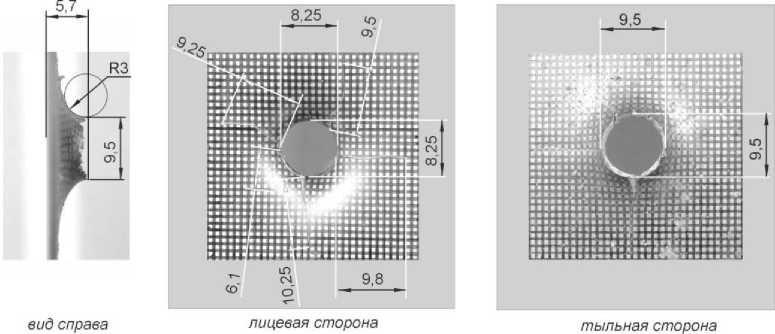
Рис. 4. Параметры повреждения экспериментального образца

Вторым этапом исследования было математическое моделирование реализованного в эксперименте процесса соударения пластины-образца со стальным шаром с использованием упомянутых выше моделей деформационного поведения и разрушения титанового сплава ВТ6. Математическое моделирование проводилось методом конечных элементов в нестационарной динамической постановке в рамках лагранжевого подхода с явной интегрирования по времени, реализованной в пакете LS-DYNA. Конечно-элементные модели пластины-образца и повреждающего предмета (шара) приведены на рис. 5. Использовались тетраэдральные изопараметрические элементы с квадратичной аппроксимацией узловых неизвестных и тремя неизвестными узловыми перемещениями. Характерный размер элемента шара-ударника составил 0,33 мм. Сетка конечных элементов пластины имеет сгущение в области соударения: характерный размер элемента – 0,33 мм, три слоя элементов по толщине. Размер элементов увеличивается по мере удаления от зоны соударения. При моделировании динамического контактного взаимодействия применен метод пенальти. Поведение материала шара – стали ШХ15 – полагалось линейно упругим без разрушения, модуль упругости Е 2.105 МПа, плотность ρ=8000 кг/м3.

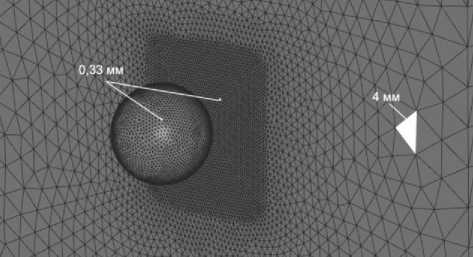
Рис. 5. Конечно-элементные модели пластины и повреждающего предмета

Модель Купера-Саймондса учитывает кинематическое упрочнение и позволяет описывать зависимость предела текучести от скорости деформации. Для учета влияния скорости деформации на предел текучести материала вводится масштабирующий коэффициент:

pp

^— eff >  ^—B ^— eff

1 t ₂

= fl - —Yp—p I dt, ij ij

0 V ³       /

P

^“ ^к = ^р ; в = 1 + | - I ,      (1)

Т     ^т          ( C )

где — - скорость деформации; а_Т - предел текучести, ^ Т“" - динамический предел текучести, С, Р – константы материала.

Критерием разрушения является достижение эффективной пластической деформаци-p ей εeff предельного значения εВ:

где 8.p - компоненты тензора скоростей пластической деформации.

Механические характеристики и параметры модели Купера-Саймондса для сплава ВТ6 по данным [1, 5-7] приведены в таблице 1. Предельное значение эффективной пластической деформации εВ для сплава ВТ6 по результатам эксперимента принято равным 0,4.

Таблица 1. Характеристики сплава ВТ6, принятые для модели Купера-Саймондса по данным [1, 5-7]

Плотность ρ , кг/м3	Модуль упругости Е , МПа	Коэффициент Пуассона μ	Предел текучести σ Т , МПа	Предел прочности σ В ,МПа	С	P
4,43∙103	122630	0,3	910	1000	20000	3

Результаты конечно-элементного моделирования с использованием модели Купера-Саймондса показали следующее. При соударении стального шара с пластиной в момент касания начинается процесс деформирования пластины и нарастание всех компонент напряжений и деформаций. Значения эффективной пластической деформации выше на тыльной стороне пластины. Зона эффективных пластических деформаций, близких к предельному значению εВ, приобретает форму кольца. Разрушение начинается на 8-ой микросекунде с момента касания. За 3 микросекунды происходит разрушение 3-х слоев элементов пластины по толщине. Образуется отверстие и «пробка» чашевидной формы. В течение следующих 24х микросекунд происходит отгиб краев отверстия и образование трещин радиального направления. По окончании взаимодействия шар не меняет своего первоначального направления движения, «пробка» движется в одном направлении с шаром. Полученное в результате моделирования повреждение представляет собой сквозное отверстие диаметром 9 мм с отгибом в сторону движения шара и наружным диаметром отогнутой части с тыльной стороны 10,1 мм (рис. 6). Высота отгиба – 4,7 мм. Длина трещин – до 3 мм. Диаметр «пробки» – 5,7 мм, высота – 1,6 мм. Поверхность разрушения – коническая с вершиной со стороны вогнутой поверхности «пробки». Скорость шара после соударения составила 327 м/с, «пробки» – 390 м/с.

Альтернативный вариант моделирования процесса соударения шара с пластиной из сплава ВТ6 выполнялся с использованием более сложной модели материала Джонсона-Кука [3]. Согласно этой модели предел текучести зависит от эффективной пластической деформации ^— ef (2), скорости изменения эффективной пластической деформации ё ef и температуры T

^ Т ^— p , f , T ) = ^[<7 Т 0 ⁺ A ^{( —} pf )

1 + C In

p eJfL

V ^- 0 7

1 +

¹ T - T o ¹

V T melt

-

T o )

ё0 и Т0 - референтные скорость деформации и температура, Тmelt – температура плавления металла, ^То - предел текучести материала при комнатной температуре, A – чувствительность к деформации, C1 – чувствительность к скорости деформации, n – параметр, отвечающий за влияние деформационного упрочнения, m – параметр, описывающий температурное разупрочнение.

В качестве критерия разрушения используется сопряженная модель Джонсона-Кука на базе кумулятивного закона накопления повре-жденности d :

p d Y e

^ £

£^p_f = d_x + d ₂ exp( d₃ — ) L                     q.

1 + d ₄ ln | f I ^£ o

1 + d s

T - T o I ,

T . -T I melt OQ)

p где £f - показатель текущего состояния элементарного объема материала – критическая интенсивность пластических деформаций, di i=1-5 – постоянные материала, p и q – первый и второй инварианты тензора напряжений.

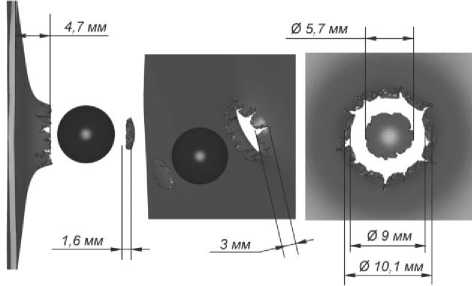
Рис. 6. Размеры повреждения-отверстия и «пробки» при использовании модели материала Купера-Саймондса

Использовались характеристики материала по данным [4,8]. Референтные скорость деформации и температура £0 = 1,0 с-1 и T0=2980 K. Разрушение начинается на 3-ей микросекунде с момента касания пластины и шара с тыльной стороны пластины. За следующие 3 микросекунды происходит образование отверстия и отделение «пробки». В течение последующих 21 мкс происходит отгиб краев отверстия, образование и рост трещин. Повреждение, как и в случае использования модели Купера-Саймондса, представляет собой сквозное отверстие с отгибом краев по направлению движения шара, присутствуют радиальные трещины. Диаметр отверстия составляет 9 мм, наружный диаметр отогнутой части с тыльной стороны 10,8 мм максимальная длина трещин – 4,4 мм, отгиб краев отверстия – 5,1 мм (рис. 7). Форма «пробки» чашевидная, габаритные размеры – 6,1х 2,4 мм. Поверхность разрушения – коническая с вершиной со стороны выпуклой поверхности «пробки». Остаточная скорость шара составила 360 м/с, скорость «пробки» – 390 м/с.

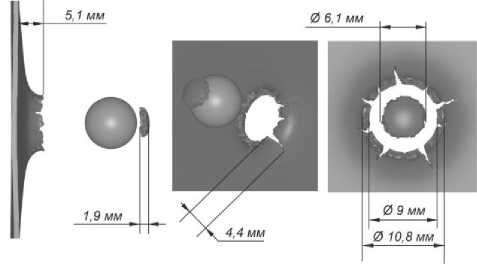
Рис. 7. Размеры повреждения-отверстия и «пробки» при использовании модели материала Джонсона-Кука

Геометрические характеристики повреждений, полученные численным анализом по обеим исследованным моделям поведения материала согласуются между собой и с экспериментальным данными (таблица 3). Расхождение по геометрическим параметрам повреждения-отверстия лежит в пределах 9,1% для модели Купера-Саймондса и 15,4% для модели Джонсона-Кука. Размеры радиальных трещин в зоне повреждения в расчете с использованием модели Купера-Саймондса в 3 раза меньше, а при использовании модели Джонсона-Кука – в 2 раза меньше чем в эксперименте. При анализе деформированного состояния «пробки» (рис. 8) несколько лучшее соответствие эксперименту получено в расчете по модели Джонсона-Кука, в частности форма поверхности разрушения согласуется с экспериментально полученной.

Таблица 3. Геометрические параметры экспериментального и расчетных повреждений

Параметр	Эксперимент	Расчет по модели Купера-Саймондса		Расчет по модели Джонсона- Кука
		значение	расхождение с экспериментом %	значение	расхождение с экспериментом %
диаметр повреждения (отверстия) с лицевой стороны, мм	8,25	9,0	9,1	9,0	9,1
диаметр повреждения (отверстия) с тыльной стороны, мм	9,5	10,1	6,3	10,8	13,7
высота отгиба, мм	4,42	4,7	6,3	5,1	15,4
диаметр пробки, мм	6,8	5,7	16,2	6,1	10,3
высота пробки, мм	2,1	1,6	23,8	1,8	14,3
длина трещин, мм	10	3,0	70	4,4	56

Рис. 8. Габаритные размеры «пробки»:

а) результат эксперимента, б) результат расчета по модели Купера-Саймондса, в) результат расчета по модели Джонсона-Кука

На рис. 9 представлены полученные в расчетах и эксперименте интенсивности пластической деформации на тыльной стороне пластины-образца в зависимости от расстояния до центра повреждения. Расчетные и экспериментальные распределения хорошо согласуются друг с другом. В расчете с использованием модели материала Купера-Саймондса максимальные значения интенсивности деформации совпадают с величиной предельной деформации до разрушения материала ε в =40%. При использовании модели Джонсона-Кука значение интенсивности пластической деформации вблизи краев отверстия получено несколько ниже, чем в эксперименте, 33%. При удалении от краев отверстия в эксперименте и расчетах пластические деформации уменьшаются.

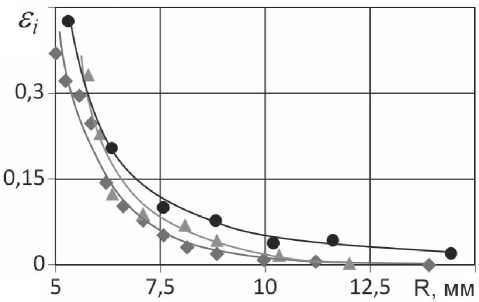
Рис. 9. Зависимость пластической деформации от расстояния до центра повреждения: ф - результат эксперимента, ♦ - результат расчета по модели Купера-Саймондса, А - результат расчета по модели Джонсона-Кука

Полученные в расчетах пластические деформации «пробки» показаны на рис. 10. В случае использования модели материала Купе-ра-Саймондса величина пластических деформаций на лицевой поверхности пластины (на поверхности соударения) меньше (до 28%), чем на тыльной, где максимальные значения совпадают с заданным предельным значением ε в =40%. При использовании модели Джонсона-Кука, наоборот, большие значения пластических деформаций наблюдаются на лицевой поверхности и достигают 48%, а на тыльной – до 28%.

тыльная сторона

тыльная сторона

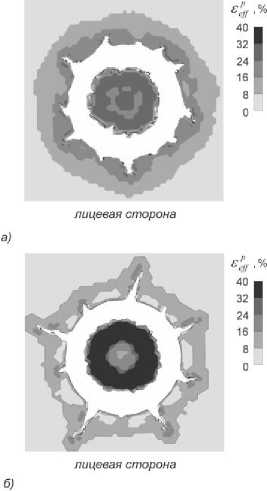
Рис. 10. Поле эффективных пластических деформаций вблизи повреждения при использовании модели материала Купера-Саймондса (а) и Джонсона-Кука (б)

Выводы: обе исследованные модели деформационного поведения и разрушения материала – Купера-Саймондса и Джонсона-Кука обеспечивают согласование расчетных данных о характере и параметрах повреждения с экспериментальными. Несколько более точное соответствие эксперименту по форме поверхности разрушения, размерам повреждения и трещин дает модель Джонсона-Кука, однако она включает в себя большее количество параметров, подлежащих экспериментальному определению.