Экспериментально-теоретические исследования теплового состояния приборного отсека фоторазведчика

По техническим, экономическим и другим причинам в процессе лётных испытаний параметры теплообмена могут быть найдены лишь для некоторых режимов полёта и некоторых теплофизических параметров воздушной среды за пределами теплового и аэродинамического пограничных слоёв у наружной поверхности обшивки. Найденные параметры теплообмена могут быть распространены на другие режимы и параметры воздушной среды за бортом путём построения математических моделей. Поэтому проведение лётных и стендовых испытаний бортового оборудования, расположенного в продуваемом теплоизолированном отсеке самолёта, требует математического моделирования теплового состояния приборного отсека.

Приборный отсек фоторазведчика представляет собой негерметизированный отсек с теплоизолированной обшивкой, продуваемый воздухом из системы обеспечения теплового режима.

Тепловое состояние отсека формируется внешними и внутренними факторами. К внешним факторам относятся теплообмен между наружной поверхностью обшивки и тепловым и аэродинамическим пограничными слоями, лучистый теплообмен наружной поверхности обшивки от Солнца, Земли и других поверхностей. Внутри отсека тепловая энергия выделяется бортовым оборудованием и отводится или подводится системой обеспечения теплового режима.

Общий подход к построению математических моделей теплообмена блоков в приборных отсеках и математических моделей теплового состояния отсеков самолёта с использованием методов идентификации предложен в работе [1]. При этом принимались следующие допущения:

• 1.    Отсек аппроксимируется системой блоков, заключенных в оболочку (обшивку). Поверхность каждого блока аппроксимируется кусочно-плоской поверхностью. Блоки и части обшивки разделены воздушными средами (каналами).

• 2.    Температура поверхности и температура объёма каждого блока и обшивки равномерны и равны друг другу.

• 3.    При лучистом теплообмене все поверхности принимаются изотермическими, серыми, диффузно-излучающими, а интегральный поток излучения – равномерно распределённым по каждой поверхности.

• 4.    Тепловой поток через узлы крепления блоков пренебрежимо мал по сравнению с конвективной и лучистой составляющими теплового потока.

Модели теплообмена бортового оборудования строятся в соответствии с законами сохранения энергии, количества движений в сочетании с законом вязкости трения Ньютона-Рихмана, законом теплопроводности Фурье и законом лучистого теплообмена Стефана-Больцмана. Эти уравнения, дополненные зависимостями физических характеристик воздушной среды от тем-– 338 – пературы, давления, времени, составляют замкнутую систему. Решение такой задачи в общем виде не представляется возможным. Поэтому используют различные допущения и упрощения исходной модели. Одним из наиболее распространенных способов упрощения является приведение модели к системе обыкновенных дифференциальных уравнений.

Математическое моделирование теплового состояния продуваемого теплоизолированного приборного отсека

Математическую модель приборного продуваемого теплоизолированного отсека с системой обеспечения теплового режима представим системой одномерных уравнений теплоизолированной обшивки и обыкновенных дифференциальных уравнений теплообмена внутренней поверхности теплоизоляции обшивки, бортового оборудования, воздуха и переноса энтальпии из системы обеспечения теплового режима.

Теплообмен теплоизолированной обшивки пусть будет равномерным по наружной и внутренней поверхностям без передачи тепла теплопроводностью по воздуху.

Уравнения теплообмена теплоизолированной обшивки представим в виде одномерных уравнений теплопроводности, описывающих процесс передачи тепла в многослойной конструкции:

C v ( х ) Tv,t = uv ( x , T cv Cv , X ) X , 0 <  x <  1 ;

^ ⁽ X , T v ) ^Т_ = ^a , out ⁽ t ) F T ⁽ t ) ^{- T (} t , X )) + ^Q , out ^- - c 0 8„ J-   JU t ),             x = 0;

T v ( X T cv ) FT' x = « cv.n ( ) ^F cv (T r ( t ) — Tv (t , X )) +

+Ъ ,. T / T s - c 0 8_ F^ T cv (t ) + Q cvn ;    x = l ;

Tcv (0, x) = T)(x), 0 < x < 1, где C„ ( x) - C, A„ (x, T) - Л, + ■ T при l^ x < l, ,„ = 1 k-1),

C cv ⁽ x ) = C k , l ev ⁽ x , TCV ) = Tc ,0 + Tc ,Tcv при l k - 1 ^ x ^ l k , ^то есть C cv , ^ cv ^{зависят от того}, в ^каком слое рассматривается перенос тепла.

^При э^{том 0} = ¹ 0 <  ¹ , < ...< l k = ¹ .

В уравнениях (1)-(4) использованы следующие обозначения: Tcv(x,t) - температура много, слойной конструкции; T – первая производная T по t; T – первая производная T по x; cv,t                                             cv             cv,x                                             cv lcv-x-x - вторая производная Tcv по x; Ccv(x) — объёмная теплоёмкость многослойной конструкции обшивки (произведение удельной теплоёмкости на плотность); Acv(l, T) - теплопроводность многослойной конструкции; acvout - коэффициент теплоотдачи наружной поверхно-, сти конструкции; αcv,in – коэффициент теплоотдачи внутренней поверхности конструкции; Fcv - площадь конструкции при наружном и внутреннем теплообмене; Qcv,out - тепловая энергия внешних источников; Qcv,in – тепловая энергия внутренних источников; c0 – постоянная Стефана-Больцмана; εcv,in – степень черноты излучения внутренней поверхности многослойной конструкции; gj,cv – коэффициент радиационного теплообмена системы «j-й элемент отсека – многослойная конструкция»; Te – температура восстановления; t – время; Tair – температура – 339 – воздушной среды в отсеке или в части отсека; Tj - температура j-го элемента отсека; l - толщина многослойной конструкции.

Параметры теплообмена, определяющие коэффициенты теплоотдачи acv,out и аcv,in для рассматриваемых условий, могут быть найдены лишь для некоторых режимов полёта и некоторых теплофизических параметров воздушной среды за пределами теплового и аэродинамического пограничных слоёв у наружной поверхности обшивки. Поэтому вычислить названные коэффициенты теплоотдачи по критериальным соотношениям в процессе лётных испытаний пока не представляется возможным [2]. Их предлагается определять из уравнений acv,out

= A, J

И, out ^и out ( t ^);

а , . = Л, J * ( t ),

где J_out , J_in – модуль массовой скорости воздушной среды за бортом и в отсеке соответственно; ^ 1 out , ^ 2 out , 3 n , A , n ^- оцениваемые коэффициенты модели.

Уравнение теплообмена бортового оборудования представим в виде обыкновенного дифференциального уравнения, описывающего его конвективный теплообмен с воздухом и конвективно-лучистый теплообмен с окружающими конструкциями:

T m , t = a air , m ( t ) F a„ , m I C m ( T a„ ( t ) — T m ) + £ g j , m I m

I CmTj (t)/ T„' — C0 8m Fm I '^' + Qm I Cm, где Tm – температура m-го бортового оборудования; Tm,t – первая производная Tm по t; αair,m – коэффициент теплоотдачи m-го бортового оборудования; Fair m - площадь m-го бортового оборудования при конвективном теплообмене; Cm – теплоёмкость m -го бортового оборудования; gj, - коэффициент радиационного теплообмена системы «j-й элемент отсека - m-й блок борт»-вого оборудования»; εm – степень черноты излучения m-го блока; Qm – энергия тепловыделения или теплопоглощения m-м бортовым оборудованием от системы обеспечения теплового режима и преобразованная из электрической энергии.

Коэффициент теплоотдачи аair,, для рассматриваемых условий пока также не представляется возможным выявлять по критериальным соотношениям. Поэтому их предлагается определять из уравнения amr ,= 9X,J 92Ч t),

где А 1 i , S ₂ i - оцениваемые коэффициенты модели.

Уравнение теплообмена воздушной среды представим в виде обыкновенного дифференциального уравнения, описывающего конвективный теплообмен внутренней поверхности теплоизоляции обшивки, элементов отсека и перенос энтальпии из одной части отсека в другую:

T ar , k,t = a cvin ( t ) F cv / C a„ k \T „ ( t , X ) — T ar , k ] +

⁺ ]L ^a ar , ^j F ar , j / C ar . k ^{( Tj} — ^Ta^r . k ) ⁺ C p J ar , k ^Fk I

I C ar , k (T ar , k - 1 - T ark );       ^ = l ;

где T_air,k-1, T_air,k – температуры воздушного потока соответственно в ( k –1)-й и k -й частях отсека;

Jaiirk — массовая скорость воздушного потока в к-й части отсека; Fk - суммарная площадь воз, душных каналов в k-й части отсека; cp – удельная теплоёмкость воздуха; Cair,k – теплоёмкость воздуха в k-й части отсека.

T_airi[ в выражении (9) с индексом t означает её дифференцирование по времени t . ar,

Суммирование в уравнении (9) ведётся по j-му элементу, входящему в к-ю часть от сека.

Теплоёмкость воздуха Cair,k определяется по выражению z—f

C air , k

c p ^P air , k

(W. , V air , ent

F air , ent ^Д t + ^Vair , k X

где ρ _{air k} – плотность воздуха в k -й части отсека; W_{air ent} – скорость воздуха на входе в отсек; ,,

Fair ent — площадь воздушных каналов на входе в первую часть отсека; At - интервал дискретиза-, ции времени при решении системы дифференциальных уравнений; Vair,k – объём воздуха в k-й части отсека.

Коэффициент радиационного теплообмена в уравнениях (3), (7) определяется методом

Монте-Карло [3].

Методы решения прямой и обратной задач теплового состояния отсека

Для решения прямой задачи теплового состояния отсека одномерные уравнения (1)–(4) для теплоизолированной обшивки дискретизируются по пространственной переменной по методу Галёркина, использующему кусочно-линейный базис. В результате применения этого метода решение уравнений (1)-(4) сводится к численному решению системы обыкновенных дифференциальных уравнений, неизвестными которой являются значения температуры в узлах заданной сетки на отрезке [0, l ]. Полученные таким образом обыкновенные дифференциальные уравнения для многослойных конструкций (1)–(4), уравнения для бортового оборудования (7) и воздушной среды (9) составляют жёсткую систему дифференциальных уравнений, которую в общем виде можно записать следующим образом:

Y = F ( Y ( t , 0 )), t е (0, t , );

Y = Y ₃, F , Y e R S ; 0e R ^r ,...

где Y=[T, T, ., T0, ...]T - вектор параметров теплового состояния отсека; Y, - вектор первых T производных Y по t; 0 = [91 out, 92 out,91 ^92 ^9..,92.] - вектор коэффициентов модели; T -верхний индекс, обозначающий операцию транспонирования.

Для решения уравнений (11) предлагается использовать следующую численную схему типа Розенброка второго порядка аппроксимации для неавтономных систем [4]:

————

Y n + 1 = Y n + aK i + (1 - a ) K₂;

K1 = h(I - ah Vy (Yn,tn,0))-1 V(Yn,tn + ah,0);

— —    —    — ——

K 2 = h ( I - ah

Y (Yn, tn, ® )y^{1 —} ¥ (Yn, tn + aK ₁₅ tn + 2 ah , 0 ); a = 1 - 1/72,

ТГ ТГ где, Yn, Yn+1 - решение системы!, полученной на n-й и (n + 1)-й итерациях соответственно;

Tf                                                            it#

Т - правая часть системы; Т _у - матрица Якоби; I - единичная матрица; h - шаг интегрирования.

Решение обратной задачи, то есть оценивание коэффициентов Θ модели, сводится к минимизации взвешенной суммы квадратов невязок между вектором параметров теплового состояния отсека Y =[ T , T , T , T , …] ^T , измеренными в летном эксперименте Z*, и 1,    2,    .,    ⁰

соответствующими значениями Z ( Y ( t , 0)), полученными в ходе расчетов по уравнениям модели

NS

Ф ( ® ) = 1 1 I Г к ,( ZVZ i ( Y ( t_k , 0 ))) ² ,                         (15)

где Г _k,i – весовые коэффициенты; t_k – моменты времени при k = 1, … , N.

Как было отмечено в работе [2], для минимизации функции (15) целесообразно использовать сочетание метода наискорейшего спуска, квазиньютоновского метода Бройдена-Флетчера-Гольдфарба-Шэнно и метода Ньютона [5].

Доверительные интервалы оценок коэффициентов 0 нелинейной математической модели теплового состояния отсека вида (8) могут быть определены с помощью ковариационной матрицы P (Θ) ошибок оценок Θ искомых коэффициентов модели (последние характеризуют отклонения вычисленных коэффициентов модели от действительных значений). При этом используется метод проецирования совместной доверительной области оценок на координатные оси пространства коэффициентов [6].

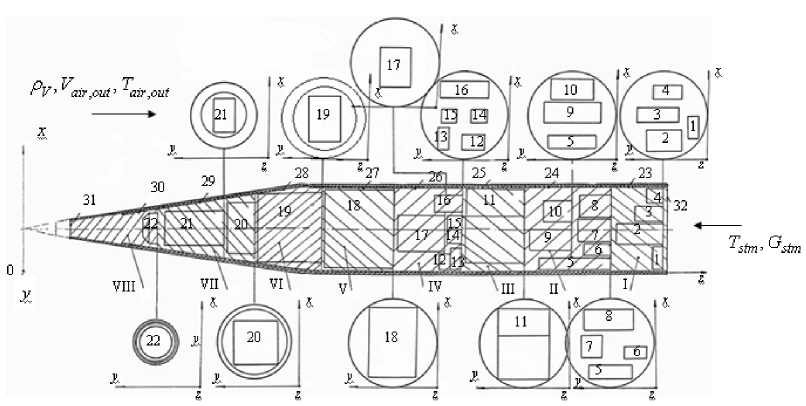
Оценивание коэффициентов модели теплового состояния отсека фоторазведчика

Компоновка приборного отсека фоторазведчика представлена на рис. 1. При этом воздух, подаваемый из системы обеспечения теплового режима, перетекает из хвостовой части отсека в носовую.

Толщина обшивки I - V частей отсека l _I-V = 2^10^-3 м, VI - VIII частей - l _VI-VII = 4^10^-3 м. Толщина теплоизоляции обшивки l_ins = 240^-2 м.

Коэффициент теплопроводности обшивки I - V частей отсека X_I-V = 2,1И0² Вт/(м\К), а VI -VIII частей к _VI-VII = 1,63Т0^-1 Вт/(м\К). Коэффициент теплопроводности теплоизоляции обшивки определяется по формуле

X i„s = - 3,6Т0^-2 + 2,8П0^-4 T ins .                                         (16)

Параметрическую идентификацию проведём по измеренным в отсеке температурам поверхности блока № 16 и внутренней поверхности теплоизоляции обшивки в районе блока № 16. При этом будем использовать результаты измерений для холодного типа климата в типовом режиме полёта фоторазведчика (рис. 2) с переменным интервалом дискретизации по времени A t = 10-300 c. Расход воздуха, выходящего из системы обеспечения теплового режима, был принят G i„s = 1 кг/с, температура T ins = 288 К.

л

Оценки 0 коэффициентов 5 1 out , 5 2 out , 5 1 in , 5 2 in , 5 1 i , 5 2 i (5), (6), (8) модели и доверительные интервалы I ₀ коэффициентов для доверительной вероятности в =0,95 имеют следующие величины:

Рис. 1. Компоновка негерметизированного продуваемого теплоизолированного отсека: I – VIII – части отсека; 1-22 – блоки бортового оборудования; 23-31 – части обшивки; x , y , z – координаты; ρ V – плотность воздушной среды за бортом; V air , out – воздушная скорость полёта; T air , out – температура воздушной среды за бортом; T stm – температура воздуха на выходе системы обеспечения теплового режима; G stm – расход воздуха на выходе системы обеспечения теплового режима

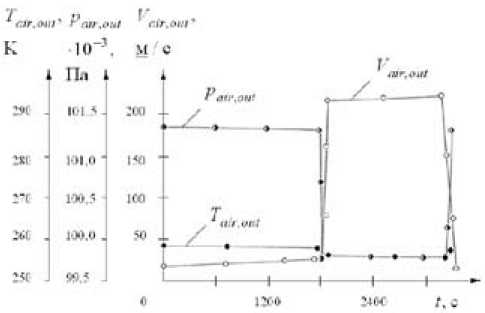
Рис. 2. Параметры режима полёта и воздушной среды за бортом фоторазведчика для холодного типа климата: P air , out – давление воздуха за бортом; T air , out – температура воздуха за бортом; V air , out – воздушная скорость полёта

0 = [0,3674 0,4238 0,0180 0,9872 0,6998 0,6102] T ;

I ₀ = [0,0390 0,0622 0,0017 0,1124 0,0633 0,5317] T .

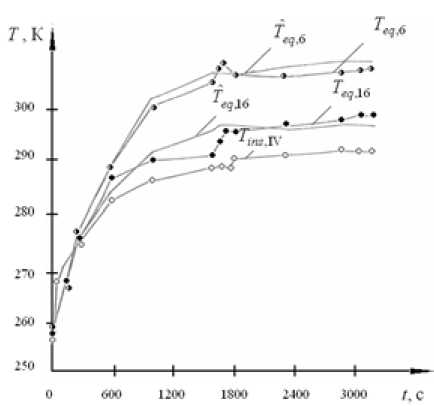
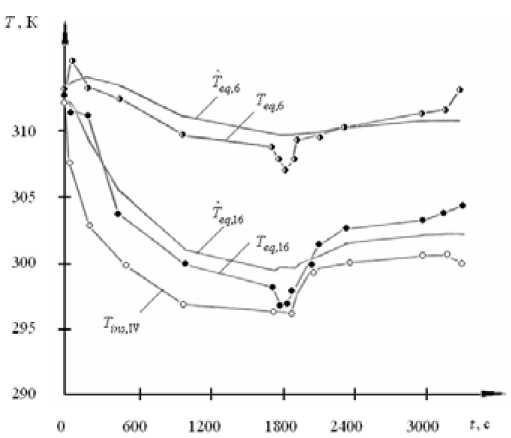
Доверительные интервалы погрешностей измерения температуры поверхностей в отсеке и температуры воздушной среды за бортом не превышали 3 К при доверительной вероятности β = 0,95, а погрешностей индикаторной земной скорости и высоты полёта – 3 %.

Для экспериментальной проверки предложенной модели на различных режимах полёта и воздушной среды за бортом, а также на элементах приборного отсека рассчитанные по модели температуры элементов отсека сравнивали с измеренными значениями.

Рис. 3. Измеренные и рассчитанные температуры поверхностей в отсеке фоторазведчика для холодного типа климата: Teq,6 – измеренная и Tˆeq,6 – рассчитанная температуры поверхности блока № 6; Teq,16 – измеренная и Tˆ   – рассчитанная температуры поверхности блока № 16; Tins IV – измеренная температура eq,16

внутренней поверхности теплоизоляции обшивки в части отсека IV в районе блока № 16

К -IO"3.

Пл

25fl

air.oul1

101.5 -

101J0 -

100^"

too jo ■

2-100

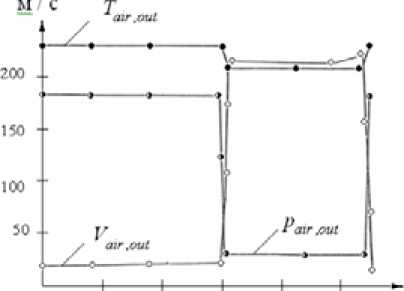
Рис. 4. Параметры режима полёта и воздушной среды за бортом фоторазведчика для тёплого типа климата: P air , out – давление воздуха за бортом; T air , out – температура воздуха за бортом; V air , out – воздушная скорость полёта

Измеренные T eq и рассчитанные по модели T ^ˆ _eq значения температуры поверхности для холодного типа климата при режиме полёта и воздушной среды за бортом, представленных на рис. 2, для блоков № 16 и № 6 приведены на рис. 3; для тёплового типа климата при режиме полёта и воздушной среды за бортом, представленных на рис. 4, даны на рис. 5. Разность между экспериментальными и рассчитанными по модели значениями температуры в этих случаях меньше 3 К. Эта величина не превышает доверительного интервала погрешности измеренной температуры.

Рис. 5. Измеренные и рассчитанные температуры поверхностей в отсеке фоторазведчика для тёплого типа климата: T_{eq ,6} – измеренная и T ^ˆ _{eq ,6} – рассчитанная температуры поверхности блока № 6; T_{eq ,16} – измеренная и T ^ˆ _{eq ,16} – рассчитанная температуры поверхности блока № 16; T ins ,IV – измеренная температура внутренней поверхности теплоизоляции обшивки в части отсека IV в районе блока № 16

Анализ остатков по критерию перестановки [7] показал, что их можно считать случайными, а анализ функций распределения остатков по критерию согласия Колмогорова-Смирнова – что они описываются нормальным законом с доверительной вероятностью β = 0,32…0,57.

Следовательно, построенная математическая модель теплового состояния приборного отсека адекватна реальному тепловому состоянию негерметичного продуваемого теплоизолированного отсека фоторазведчика.

Заключение

Для проведения лётных и стендовых испытаний бортового оборудования, расположенного в продуваемом теплоизолированном отсеке фоторазведчика, предложен экспериментальнотеоретический метод, включающий математическое моделирование теплового состояния приборного отсека, параметрическую идентификацию модели, определение погрешностей коэффициентов модели и проверку адекватности модели.

Математическая модель приборного продуваемого теплоизолированного отсека с системой обеспечения теплового режима построена в виде системы одномерных уравнений теплоизолированной обшивки и обыкновенных дифференциальных уравнений теплообмена внутренней поверхности теплоизоляции обшивки, бортового оборудования, воздуха и переноса энтальпии из системы обеспечения теплового режима.

В качестве метода параметрической идентификации модели теплового состояния отсека использовано сочетание метода наискорейшего спуска, квазиньютоновского метода Бройдена-Флетчера-Гольдфарба-Шэнно и метода Ньютона. Для решения прямой задачи, то есть решения жёсткой системы обыкновенных дифференциальных уравнений, – неявный метод Розенброка второго порядка.

Доверительные интервалы оценок коэффициентов нелинейной математической модели теплового состояния отсека определены с помощью ковариационной матрицы ошибок оценок искомых коэффициентов модели.

Выбраны критерии проверки адекватности модели по анализу остатков и доказана адекватность построенной математической модели реальному тепловому состоянию негерметичного продуваемого теплоизолированного отсека фоторазведчика.