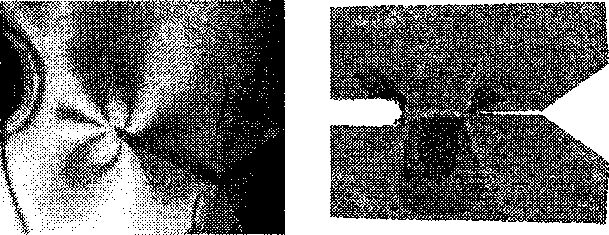Экспериментальное и теоретическое исследование нелинейной динамики трещины

Хрупкое разрушение, один из самых удивительных феноменов физики твёрдого тела, притягивает большой интерес исследователей на протяжении многих десятилетий. Несмотря на значительный объём экспериментальных исследований [2,8,16] и теоретических попыток объяснить механизмы, ведущие к разрушению [5,7,9,11], в настоящее время не существует полного понимания этих процессов. Необъяснимые эффекты наблюдаются даже в простых по структуре материалах

На особенности распространения трещины влияет множество внешних причин' геометрия образца, величина и способ приложения нагрузки, скорость распространения трещины и т. д.. Учет всех этих факторов в рамках классической механики разрушения не даёт реалистичной картины процесса, так как оставляет без внимания эволюцию структуры материала. Фрактографии поверхности излома демонстрируют ярко выраженный фрактальный характер [1,12] и содержат информацию о процессах, происходящих в ансамбле мезоскопических дефектов на пути распространяющейся трещины Автомодельный характер распредения напряжений в носике трещины позволяет предположить, что определяющее влияние на характер распространения оказывает эволюция структуры материала в зоне непосредственно перед носиком движущейся трещины (в так называемой зоне процесса). В работе [16] был поставлен простой, с точки зрения напряжённо-деформированного состояния, но физически содержательный эксперимент. Внешние условия были подобраны таким образом, чтобы в процессе распространения трещины скорость диссипации энергии в носике трещины ( а следовательно и средняя скорость трещины ) поддерживалась постоянной. В результате были обнаружены следующие закономерности распространения трещин в хрупкой аморфной среде:

• •    скорость не может достигать теоретически установленной предельной скорости распространения трещины в упругой среде ( С_к - скорость распространения волны Релея), а ограничена значительно меньшим значением,

• •    существует критическая скорость распространения трещины (*0,3(>С_к), выше которой невозможно устойчивое прямолинейное распространение

• п оследней; критическая скорость является константой материала и не зависит от геометрии образца и условий нагружения;

• •    при достижении трещиной критической скорости начинаются не только осцилляции скорости трещины, но и ветвление её следа. Осцилляции скорости распространения и длина боковых ветвей трещины хорошо коррелируют между собой и увеличиваются с возрастанием средней скорости.

В данной работе на основании статистической теории дефектов, развитой в [3,13], получены определяющие соотношения для упругого тела с микротрещинами. Дано качественное объяснение механизмов, ограничивающих скорость прямолинейного распространения трещины и управляющие её ветвлением. Получены новые экспериментальные данные по распространению трещин в РММА. Проведено численное моделирование распространения трещины в реальных экспериментальных образцах.

Статистическая модель. Определяющие соотношения. Пространственно-временные структуры в ансамбле дефектов

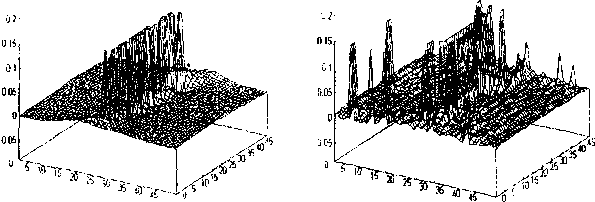
Описание кинематики и термодинамики сред с дефектами может быть основано на использовании идей калибровочной теории, содержательным результатом которой является введение дефектов произвольного типа как локализации группы симметрий тензора дисторсии. В данной работе построение калибровочного поля выполняется не с формальных макроскопических позиций, а с микромеханической точки зрения. В качестве причины, вызывающей трансляционное нарушение диффеоморфизма на микроуровне, рассматривается появление микротрещины нормального отрыва. Концентрация микротрещин в твёрдом теле достигает величин 1012 э- 10й см’"3 и эволюция ансамбля микротрещин близка к эволюции термодинамической системы. Ориентацию и объём единичной микротрещины будем характеризовать тензором

(О

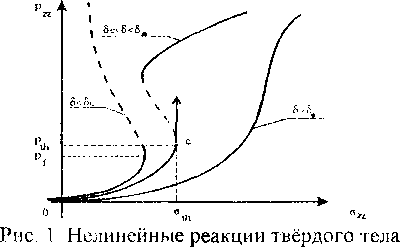
S-, =sv-v. , ik i k’ где s - объём микротрещины, v - нормальный вектор к плоскости микротрещины Статистическое описание ансамбля микродефектов было получено в [13]. В зависимости от размера характерной неоднородности lg (размер зёрен, блоков) и корреляционного радиуса взаимодействия между дефектами 1С можно различить три основные реакции твёрдого тела на рост дефектов в зависимости от величины безразмерного параметра

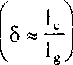
(рис. 1): монотонная 18 >5,

метастабильная

(8. > 8 > 8 су и неустойчивая (8 < 8 с у ,

Смена характерных реакций является топологическим переходом, который ведёт к качественно новому изменению симметрии системы, вызванному новым типом организации в ансамбле дефектов (первоначальное изменение симметрийных свойств было вызвано появлением дефектов).

Свободная энергия, отражающая спектр реакций твёрдого тела на рост дефектов, может быть представлена в виде

F = ™А(1- ^-)p?k + jp[k + ^С(1 - ^-)pfk + Daikpik + yx(VPik)2’ <2) 2        о *        4 и о 0                     2

где А ,В,С и D параметры разложения. Принимая во внимание полярный характер взаимодействия между дефектами, в выражение для свободной энергии добавлено

1              2

слагаемое ~x(Vpik) , отражающее эффекты нелокальности при взаимодействии дефектов, % - коэффициент нелокальности.

на рост микротрещин.

Термодинамика среды с этим типом дефектов была развита в [13], где было показано, что для квазихрупкого разрушения монотонное накопление повреждаемости сменяется при достижении некоторого критического значения напряжения взрывообразным ростом микротрещин. Используя подход Гинзбурга-Ландау [10] и с учётом (2), кинетическое уравнение для тензора плотности микротрещин может быть записано в виде dp,k = _г + a L apik , dt 5р,к Эх, V дХ] )

где Г -кинетический коэффициент, ( = Г’х. Уравнение для определения деформации в изотропной среде может быть записано в виде

Eik + 2к°"5* +C>Pik(4)

Выражения (3),(4) с разложением свободной энергии в виде (2) представляют собой определяющие соотношения твёрдого тела с дефектами. В случае квазихрупкого разрушения ^5<8С) при переходе через рс рост р(как правило, одной из pik компонент) управляется старшими степенями в разложении (2). Предполагая степенной закон для параметра нелокальности, приведём уравнение (3) к виду

|T«S'?OP-^(wPjP5|y.         о где р — р/ рс, со = 5/3. В [4] показано, что на развитой стадии процесса существуют автомодельные решения, которые при t -> tc ( tc - так называемое время обострения [4]) могут быть представлены как p-q(W),                          (6)

где g(t) = g(1 - t /1[) ” управляет законом роста структур на спектре пространственных масштабов С, (спектр собственных чисел); ф определяет изменение полуширины области локализации; G > 0 и m > О параметры, являющиеся комбинацией констант разложения (2).

Применим изложенную выше пространственно-временную кинетику ансамбля микротрещин для объяснения особенностей процесса распространения трещины. Взаимодействие макротрещины и ансамбля микродефектов в зоне процесса (в непосредственной близости к носику трещины) включает две стадии. Первая -формирование автомодельного профиля распределения плотности микродефектов в зоне процесса. Образование самоподобного профиля ведёт на второй стадии процесса к взрывообразному росту плотности микротрещин, локализованному на спектре пространственных масштабов, и появлению макроскопических структур в ансамбле дефектов. Взаимодействие основной трещины с этими новыми макроскопическими объектами определяет особенности распространения трещины. Размер зоны формирования структур (дочерних трещин) определяется величиной напряжений и зависит от начального состояния материала. Автомодельные решения уравнения (5) содержат два внутренних параметра: фундаментальную длину LT и время локализации тс. Время тс складывается из двух частей: t] - период формирования пространственного распределения в ансамбле дефектов, близкого к автомодельному, и t2 -так называемое время фокусировки [4]. Значения LT и тс определяют критическую скорость прямолинейного распространения трещины,

V..b-                           (8)

1С

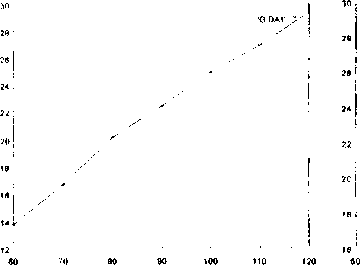
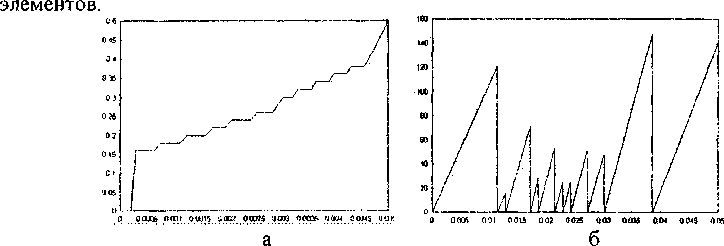
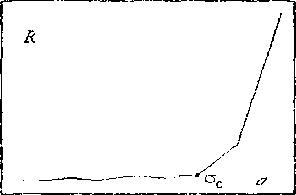
Прямолинейное распространение трещины реализуется в случае, если внешние условия обеспечивают интервал времени, достаточный для создания автомодельного профиля в ансамбле дефектов на пути распространения трещины, и скорость трещины не достигает Vc. Это означает, что в зоне процесса формирования дочерних трещин напряжения, обеспечивающие необходимые условия для самоорганизации в ансамбле дефектов (о>ос), достигнуты на масштабе LT и сохраняются в период времени t = —^tc, в этом случае дочерняя трещина образуется по направлению V распространения основной. При скоростях V > Vc эти условия нарушаются, так как LT

-^-

!

о^К,г"2Гу(6),                       (9)

(где Kj - коэффициент интенсивности напряжений, г,0 - полярные координаты точки в зоне процесса ) можно определить угол ветвления ф. Это направление, по которому внешние условия при данном коэффициенте интенсивности напряжений обеспечивают существование критических напряжений на длине LT в течение t = tc,

i f96(6*) = ^cKI Ly.                           (10)

Дальнейшее увеличение скорости трещины обеспечивается расширением зоны процесса (масштабом ветвления) и множественным зарождением автомодельных структур [13].

Экспериментальные исследования распространения трещины

Экспериментальное исследование динамики роста трещин может быть выполнено при помощи различных методов. Метод, который использован в [8,16], позволяет с хорошей точностью измерять скорость движения трещины благодаря высокой частоте отсчетов по времени. Использование подобных методик даёт возможность исследовать статистические закономерности при распространения трещин Суть метода заключается в измерении электрического сопротивления тонкого слоя металла, напыленного на поверхность образца и разрываемого при движении трещины Имеется однозначное соответствие между сопротивлением и координатой носика трещины Другой вид экспериментов основан на скоростной киносъемке движущейся трещины. Он позволяет фиксировать распределение интенсивности напряжений при использовании явления фотоупругости или теневого метода [б]. В рамках данной работы были проведены эксперименты с использованием скоростной видеокамеры, выполняющей серию из 8 снимков с выдержкой от 100 нс и с интервалом между снимками от 0 до 20 мс. На рис. 2. дана картина распределения напряжений в зоне перед движущейся трещиной (выполнено в поляризованном свете). Тёмные и светлые полосы на образце соответствуют линиям постоянных касательных напряжений Для сравнения было произведено статическое моделирование нагружения для той же длины трещины при помощи ANSYS53 (см. рис. 2). Сравнение экспериментальной динамической картины распределения напряжений и вычисленной статической показывает качественное подобие распределения напряжений в обоих случаях.

Рис 2. Распределение напряжений вблизи носика трещины: слева - эксперимент, справа - расчет

Рис. 3. Графики зависимости координаты носика т рещины от времени а - V=270 м/с, б - V=200 м/с

По сериям снимков были построены графики зависимости координаты носика трещины от времени (рис. 3).

Эти данные позволили оценить скорость трещины, которая несмотря на существенно неоднородное распределение напряжений сохранялась практически постоянной. Это показывает определяющее влияние распределения напряжений в области носика трещины на динамику её роста.

Компьютерное моделирование распространения трещины

Особенности перехода от накопления микродефектов к макроскопичекому разрушению исследовались численно, с использованием метода конечных элементов. Система уравнений включает:

доу

• •    уравнение равновесия                    = 0;(11)

• •    определяющие соотношения для изотропного упругого тела с микротрещинами Ш =Еуу (еи-ры);(12)

• •    кинетическое уравнение для тензора плотности микротрещин /                                     \ 6, д )

PiJ = -Lp^AplJ+Bplkplj+CpikpldPii+Daijj+— р^.(13)

Феноменологические параметры Lp , A,B,C,D,0) определялись путём аппроксимации типичных кривых длительной прочности для РММА [2],

А = -3,Ш0п, В = 1,71012, С=1,01012, со = 1,0 ■ 10-2.(14)

Выбор граничных условий определяется типом моделируемого эксперимента. Начальная неоднородность материала задавалась статистическим разбросом кинетических коэффициентов (L « / , где т - время релаксации ) для каждого р /тр конечного элемента (число элементов достигает 104). Статистическое распределение для Lp принималось в виде распределения Вейбула в форме

f(x) = аХхга"‘ехр (-Хх“) .                        (15)

На каждом шаге по времени вычислялись новые значения напряжений и деформаций, принимая во внимание достигнутый уровень повреждаемости. Элемент считался разрушенным, если значение какой-либо из компонент тензора р превысило критическое значение ( оценка рс = 1,0* 10"2 экспериментально полученное в [2]). Начальная трещина задавалась в центре образца в виде линии из разрушенных

Рис. 4. Динамика трещины: а - зависимость длины трещины от времени, б - зависимость скорости трещины от её длины

В работах [8,16] показано, что резкий переход от распространения единичной трещины к множественному ветвлению наблюдается при скорости выше критической , vc =0,36VR. На рис. 5 представлен средний поперечный размер перколяционного кластера из разрушенных элементов в зависимости от приложенного напряжения (при средней скорости трещины). При переходе через критическое напряжение длина боковых ветвей начинает увеличиваться.

Рис. 5. Средняя длина боковых ветвей R в зависимости от приложенного напряжения а

Рис. 6. Пространственное распределение плотности дефектов для различных уровней напряжения

На рис. 6 представлены характерные пространственные распределения плотности дефектов ( компоненты р у, отвечающей за появление дефектов нормального отрыва ) в некоторый момент времени при напряжениях ниже (а) и выше (б) критического.

Выводы

Основным результатом данной работы можно считать установление взаимосвязи между характерными структурами, образующимися на поверхности излома, и коллективными свойствами ансамбля мезодефектов в материале, и, как следствие, определение основных механизмов, управляющих распространением трещины и её ветвлением. На основании полученных определяющих соотношений численно исследован процесс перехода от устойчивого к ветвящемуся режиму распространения трещины. Результаты хорошо согласуются с экспериментальными данными. Экспериментально подтверждено существование устойчивого режима распространения при скоростях меньше 0,36* CR