Экспериментальное исследование геометрических параметров электронного луча

Наиболее существенным и одновременно наиболее трудноопределимым параметром электронного луча является его диаметр. Существует много различных способов экспериментального определения диаметра электронного луча. Среди них можно выделить группу методов, основанных на измерении распределения плотности энергии в поперечном сечении электронного луча [1-3]. Эти методы дают полную информацию об электронном луче как о технологическом инструменте. По их данным можно судить о характере распределения энергии в поперечном сечении электронного луча, степени его фокусировки и состоянии катодного узла электронно-лучевой пушки.

Обычно диаметр электронного луча определяют как ширину плотности распределения через среднее квадратическое отклонение О, а сама плотность распределения считается распределенной по нормальному закону [1...3]. Однако существуют факторы, которые приводят к отклонению формы распределения от нормального закона [1]. На форму распределения оказывают влияние оптическая система электроннолучевой пушки, состояние ее катодного узла, изменение параметров сварки. Наличие разнообразных факторов, влияющих на изменение распределения плотности энергии луча, приводит к тому, что однозначного соотношения между средним квадратическим отклонением электронов луча О и диаметром электронного луча d как энергетической оценкой вносимой удельной мощности q ₂ нет.

Помимо диаметра электронного луча, распределение плотности может быть охарактеризовано относительными коэффициентами, зависящими от формы распределения: контрэксцессах и энтропийного коэффициента кз могут быть использованы для идентификации закона распределения [4].

Для исследования параметров распределения плотности энергии электронного луча была разработана автоматизированная система исследования геометрических параметров распределения плотности энергии электронного луча (рис. 1).

Автоматизированная система состоит из двух основных блоков: канала управления лучом (КУЛ) и канала регистрации (КР).

Канал управления лучом осуществляет вывод луча из сварочной ванны и пересечение лучом зоны обзора датчика геометрии электронного луча Д в прямом и обратном направлении. Сканирование луча производится по заранее заданным траекториям, хранимым в ЭВМ. Сигналы, управляющие электронным лучом, поступают с каналов А и В устройства управления положением луча (УУПЛ) в отклоняющие системы ОС _х и ОС _у через усилители постоянного тока УПТ. Канал С используется для синхронизации устройства регистрации (УР). В качестве УУПЛ используется цифровой двухканальный генератор сигналов произвольной формы АНР-3000 фирмы «АК-ТАКОМ», представляющий собой дополнительную ISA-плату к персональному компьютеру

Технические характеристики генератора АНР-3000 следующие:

• -    количество каналов - 2;

• -    диапазон напряжений - 5.. .5 В (0.. .10 В);

• -    частота выходного сигнала - 20 МГц (1 канал), 10 МГц (2 канала);

• -    объем памяти - 2 048 точек на канал;

• -    разрешение - 8 бит;

• - режимыработы: периодический, синхронизированный, внешний запуск, ручной запуск;

• -    синхронизатор - TTL-совместимый вход-выход.

Канал регистрации осуществляет измерение сигнала, поступающего с датчика, фиксирование его в памяти ЭВМ и отображение на экране монитора. Основным узлом канала является устройство регистрации. Запуск УР производится в начале каждого сканирования синхроимпульсом (СИ), поступающим на вход канала синхронизации Е. После запуска КР выполняет измерение сигнала, поступающего на вход канала А с датчика геометрии электронного луча Д через предварительный усилитель (ПУ). Измеренный сигнал отображается на экране монитора и записывается в память ЭВМ. В качестве устройства регистрации используется двухканальный цифровой осциллограф АСК-3151 фирмы «АКТАКОМ» со следующими характеристиками:

• -    число каналов - 2;

• -    разрешение каналов - 8 бит;

  

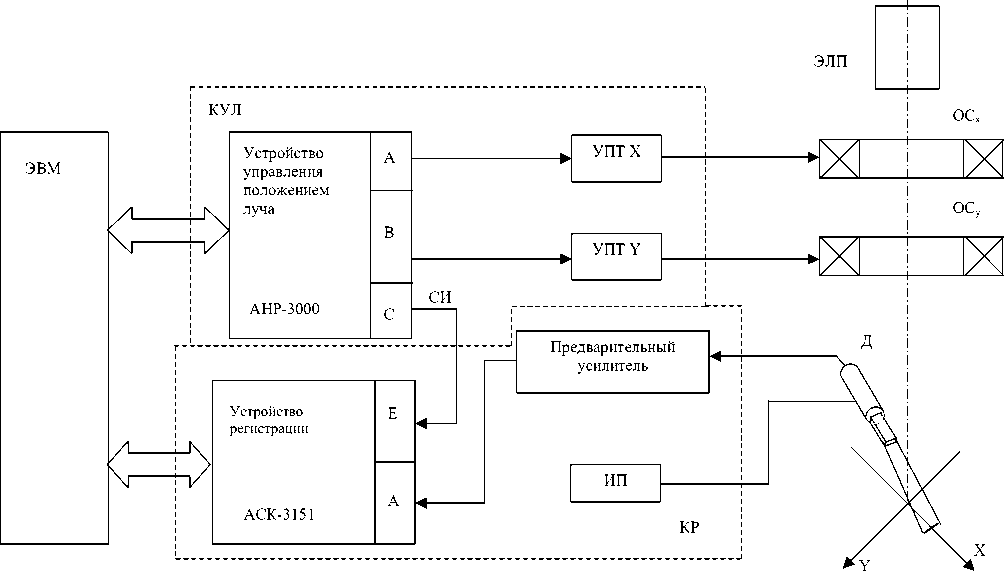
  Рис. 1. Структурная схема автоматизированной системы исследования геометрических параметров

  распределения плотности энергии электронного луча

  
  

• -    память -32 Кбайта/канал;

• -    полоса пропускания -150 МГц;

• - развертка-10мВ/дел. ...5В/дел.;

• -    максимальное допустимое входное напряжение -±100В;

  -дополнительные функции: самописец; быстрое преобразование Фурье.

Осциллограф АСК-3151 выполнен в виде отдельного блока. Для связи с персональным компьютером используется параллельный порт.

К работе устройств АНР-3000 и АСК-3151 к ЭВМ предъявляются следующие требования:

• -    IBM PS совместимый компьютер на базе процессора Pentium II233 МГц и выше;

• - ОЗУ минимум 16 Мб;

• - 10 Мб дискового пространства;

• -    операционная система Windows 95/98.

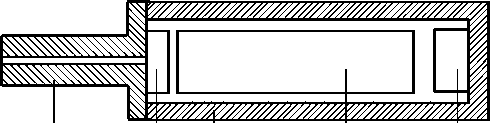
В качестве датчика геометрии электронного луча используется коллимированный рентгеновский датчик (рис. 2).

где Н ( х ) - энтропия распределения;

плотности тока [4]:

Рис. 2. Датчик геометрии электронного луча: 1 - корпус; 2 - коллиматор; 3 - сцинтиллятор; 4 - фотоэлектронный умножитель; 5 - предусилитель

Корпус датчика выполнен из материала, поглощающего рентгеновское излучение. Для ограничения зоны обзора рентгеновского датчика на его корпус надевается щелевая бленда, также выполненная из рентгенопоглощающих материалов.

Сцинтиллятор представляет собой цилиндр (или таблетку), внутри которого находятся кристаллы солиNaJ и CsJ, активированные таллием, CaF ₂ , BiGe ₃ O ₁₂ . Сцинтиллятор преобразует рентгеновское излучение в световые импульсы, интенсивность и частота которых пропорциональны мощности и жесткости рентгеновского излучения.

Фотоэлектронный умножитель предназначен для усиления световых импульсов, генерируемых сцинтиллятором, и их преобразования в электрический ток. Он состоит из полупрозрачного кремневого фотокатода, системы электростатической фокусировки электронов, динодной системы умножения с торцевым оптическим входом. Питание фотоэлектрического умножителя осуществляется высоковольтным источником питания (ИП).

В ходе проводимых экспериментов исследовались следующие геометрические параметры распределения:

• 1)    энтропийная оценка ширины распределения плотности тока луча - энтропийный диаметр [5]

  d _э = exp( H ( x )) ,

  
  

• 2)    информационные признаки формы распределения

• -    энтропийный коэффициент k _э = — exp( H ( x )) ;

2 о

I о ⁴/ / Р 4 ^,

- контрэксцесс Х =

где о - среднее квадрати

ческое отклонение распределения плотности тока электронного луча; д ₄ - четвертый центральный момент распределения плотности тока электронного луча.

Измерения проводились на установке ЭЛУ-5 с электронно-лучевой пушкой КЭП-2М и источником питания У-250. Амплитуда сканирования составляя 3,2 мм, число точек сканирования - 32. Перемещение луча из одной точки в другую соответствует 0,1 мм.

В ходе проведенных исследований были получены зондовые характеристики датчика геометрии электронного луча при различных токах фокусирующей системы I ^ Для уменьшения влияния помех и нестабильности параметров сварки для каждого значения тока фокусирующей системы снималась серия измерений, состоящая из восьми реализаций, по которым строилась осред-ненная зондовая характеристика (рис. 3). Результаты расчета геометрических параметров распределения приведены в табл. 1. Реализация № 9 в каждой серии измерений является осредненной зондовой характеристикой.

Распределение значений контрэксцесса достаточно симметрично, в то время как распределение энтропийного коэффициента неравномерно и имеет максимум в диапазоне значений 1,9...2,1 (рис. 4).

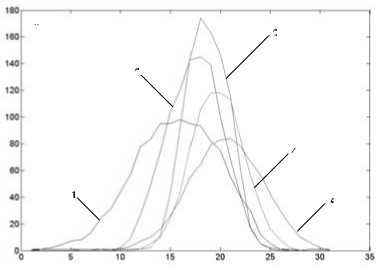
Рис. 3. Зондовые характеристики плотности тока электронного луча, соответствующие различным значениям тока фокусирующей системы: 1 -I _ф = 127 мА; 2 - I ф = 129 мА; 3-I = 132мА; 4- I =134мА;5- 1 =136мА ф                 ’          ф                 ’ ф

Таблица 1

Геометрические параметры, полученные по зондовым характеристикам датчика геометрии электронного луча

Номер серии	Номер реализации	Ток фокуса, мА	d , , - мм	х	к 3
1	1	0,127	1,768	0,574	2,003
	2		1,649	0,578	1,978
	3		1,724	0,600	2,011
	4		1,724	0,600	2,011
	5		1,664	0,573	1,984
	6		1,764	0,600	2,016
	7		1,709	0,561	2,008
	8		1,660	0,580	1,976
	9		1,701	0,585	2,006
2	1	0,129	1,155	0,483	2,006
	2		1,227	0,409	1,942
	3		1,160	0,467	2,003
	4		1,251	0,397	1,915
	5		1,225	0,387	1,914
	6		1,159	0,471	2,007
	7		1,173	0,439	1,978
	8		1,194	0,446	1,999
	9		1,162	0,442	1,986
3	1	0,132	0,957	0,339	1,633
	2		0,908	0,311	1,770
	3		0,939	0,376	1,684
	4		0,957	0,365	1,707
	5		0,882	0,465	1.727
	6		0,988	0,340	1,648
	7		0,863	0,599	1,791
	8		0,946	0,409	1,692
	9		0,953	0,377	1,700
4	1	0,134	1,123	0,422	1,864
	2		1,122	0,431	1,897
	3		1,213	0,379	1,869
	4		1,100	0,479	1,892
	5		1,102	0,448	1,891
	6		1,104	0,422	1,858
	7		1,261	0,386	1,842
	8		1,107	0,375	1,849
	9		1,082	0,473	1,917
5	1	0,136	1,540	0,600	2,003
	2		1,510	0,580	2,011
	3		1,514	0,526	1,938
	4		1,427	0,623	1,992
	5		1,572	0,509	1,983
	6		1.517	0,559	1,989
	7		1,517	0,559	1,989
	8		1,512	0,579	1,985
	9		1,499	0,597	2,006

Примечание. В табл. 1 применяются следующие условные обозначения: d -энтропийный диаметр; х - контрэксцесс; к _з - энтропийный коэффициент.

Представим поле информационных признаков формы энтропийного коэффициента и контрэксцесса с нанесенными на него отображающими точками, соответствующими полученным зондовым характеристикам (рис. 5). На поле признаков кривой, проходящей через точки 1-2-3-4-5, соответствуют одномодальные экспоненциальные распределения. Точка 4 на данной кривой характеризует расположение нормального закона, точ ка 5 - расположение равномерного распределения, точка 3 - распределение Лапласа. Отображающие точки экспериментальных распределений, нанесенные на поле признаков, указывают на близость к одному из законов распределения, изображенных в виде линии, и позволяют отнести полученное экспериментальное распределение к одной из известных аналитических моделей распределений [4].

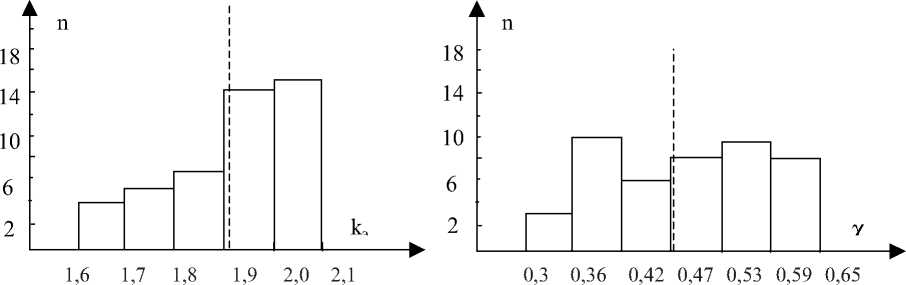
Рис. 4. Гистограмма распределения энтропийного коэффициента к _э и контрэксцесса х

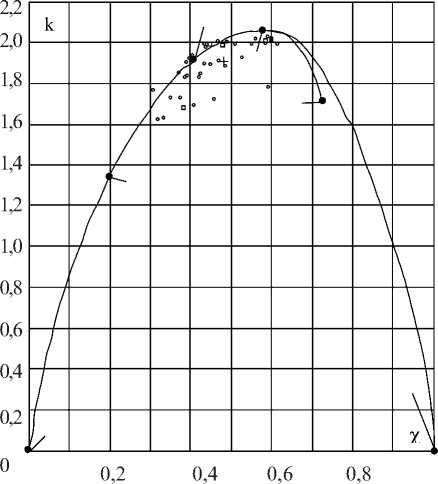
Рис. 5. Расположение экспериментально полученных распределений на плоскости признаков контрэксцесса и энтропийного коэффициента

Расположение точек показывает, что значения контрэксцесса х находятся в пределах от 0,30 до 0,62, а значения энтропийного коэффициента - в пределах от 1,60 до 2,02. Вычисление средних значений энтропийного коэффициента и контрэксцесса для всех отображающих точек дает значение к _з = 1,91 их = 0,48. Эти координаты помечены на рис. 5 прямым крестом. Все осредненные характеристики отмечены квадратом. Большая часть распределения не описывается нормальным законом, а близка к экспоненциальным распределениям.

В результате проведенных исследований была получена выборка геометрических параметров, характеризующих распределение плотности энергии электронного луча, т. е. энтропийный коэффициент, контрэксцесс и эн тропийный диаметр. Разброс значений каждого из параметров в полной мере может быть охарактеризован зако ном распределения плотности вероятности, или количе ственными характеристиками: среднеквадратическим отклонением и доверительной погрешностью.

Главным фактором, затрудняющим определение точности по законам распределения исследуемой величины, является относительно малая выборка экспериментальных данных, т. е. случайность возникновения различных значений случайной величины. Надежным путем преодоления этого разброса является увеличение объема полученных данных. Однако это не всегда возможно из-за условий проведения измерений. Поэтому все усилия направлены на то, чтобы получить параметры распределения по малой случайной выборке. При этом опираются на максимальное использование априорной информации о виде распределения, заключающейся в том, что кривая плотности распределения предполагается плавной и симметричной.

Для вычисления среднего квадратического отклонения 8 выборки значений энтропийного коэффициена, контрэксцесса и энтропийного диаметра воспользуемся следующим выражением:

n

Ц X i - »' , ) 2

i = 1

n -1

,

где и - объем выборки случайной величины;^д - координата центра распределения; х. - значение случайной величины.

Перейдем от среднего квадратического отклонения к доверительной погрешности ±А, определяющей интервал, в котором действительное значение измеряемой величины будет находиться с заданной доверительной вероятностью. Значение доверительной погрешности можно выразить в долях среднеквадратического отклонения 8 для различных значений доверительной вероятности. При этом данное соотношение зависит от закона распределения. Доверительная погрешность Ао 9, определяющая интервал для доверительной вероятности Рд= 0,9, обладает уникальным свойством: для широкого класса наиболее употребительных законов только она имеет однозначное соотношение со среднеквадратичным отклонением в виде А0,9 = 1,65.

Последовательность вычисления погрешности по экспериментальным данным следующая:

• 1.    Для каждой отдельной реализации из серии измерений (табл. 1) определяют значения геометрических параметров: контрэксцесса %, энтропийного коэффициента к _з и энтропийного диаметра d _з .

• 2.    Производят статистическую обработку полученных выборок значений контрэксцесса, энтропийного коэффициента и энтропийного диаметра и определяют среднее квадратическое отклонение для каждой выборки.

• 3.    Вычисляют доверительную погрешность А _{о д} .

Результаты расчета погрешности контрэксцесса %, энтропийного коэффициента к и энтропийного диаметра d _з для пяти экспериментальных серий (каждая серия состоит из восьми реализаций) представлены в табл. 2,3. (А _отн (х), А _отн ( к _з ), А _отн ( d _з ) - относительные погрешности).

Как видно по расчету погрешности, точность измерения геометрических параметров электронного луча является вполне удовлетворительной. Однако точка, соответствующая острому фокусу, оказалась наиболее подверженной воздействию случайных помех, исказивших результаты измерения.

В заключение сделаем следующие выводы:

• -    для уменьшения влияния помех расчет геометрических параметров следует производить по осредненным зондовым характеристикам, полученные параметры распределения по отдельным реализациям использовать для оценки точности проведенных измерений;

• -    большинство полученных распределений не описываются нормальным законом, а близки к экспоненциальным распределениям;

• -    точка, соответствующая острому фокусу, наиболее подвержена воздействию факторов, искажающих результаты измерения.