Экспериментальное исследование кинематики двухрядной планетарной передачи эллиптическими зубчатыми колесами с двумя внешними зацеплениями

Оригинальное эмпирическое исследование

Original Empirical Research

Experimental Study of the Kinematics of a Double-Row Planetary Mechanism

Using Two Elliptical External Gears

Alexander A. Prikhodko © И , Nataliya N. Belina © , Andrey V. Novitsky ® , Maksim M. Shchetinin

Kuban State Technological University, Krasnodar, Russian Federation

Introduction . Mechanisms with non-circular gears are of wide interest to researchers and inventors due to their compactness and the implementation of a wide range of transfer functions. The development of this area is stimulated by the advancements and reduction in cost of mechanical processing and additive manufacturing technologies, as well as the use of applied mathematical modeling packages for the analysis and synthesis of non-circular gears. Traditionally, noncircular gears are used to transmit rotational motion between parallel axes with a variable ratio of angular velocities. However, their use in planetary gear schemes provides implementing various types of output link motion. The analysis of the papers on the research area shows that gears with movable rotation axes have not been sufficiently studied from the point of view of kinematics and dynamics. Most research papers reveal the theory of such mechanisms without verifying the results obtained in practice. This work is aimed at the experimental verification of the kinematics of a planetary mechanism with two external engagements, which contains elliptical gears.

Materials and Methods. The kinematic model of the mechanism under study is built on the basis of the velocity diagram of its links, which made it possible to obtain expressions for finding an analogue of the angular velocity and the position function of the output shaft. The experimental study of kinematics was performed on a laboratory stand containing a model of a planetary mechanism with a set of replaceable gear wheels, absolute encoders on the input and output shafts of the mechanism, a controller, and a PC for recording and processing the signal. The analysis of the obtained results was performed on a computer using statistical analysis methods.

Results . As a result of kinematic analysis, position functions were constructed for three alternative planetary mechanisms, which had different geometric parameters of the gears and made it possible to implement various types of motion of the output shaft: swinging motion, discontinuous motion, and unilateral uneven rotation.

Discussion and Conclusion. The analysis of the experimental results showed the adequacy of the constructed mathematical model of kinematics to real mechanisms. The confidence interval of measuring errors at a reliability level of 95% was 0.16±0.08° for the first version of the mechanism, 0.57±0.22° — for the second version, and 0.08±0.26° — for the third. The proposed planetary mechanism with elliptical gears for implementing various types of motion can be used in drives of process equipment in numerous industries: chemical and food (mixers), oil refining (pumping units for crude production), mechanical engineering (compressors, pumps, automated machines), and others. The conducted kinematic studies of the planetary mechanism and their experimental analysis are needed for further dynamic and force investigations, as well as for the design of drives based on the proposed transmission.

Acknowledgements . The authors would like to thank the Editorial board and the reviewers for their attentive attitude to the article and for the specified comments that improved its quality.

Funding Information. The work was done with the financial support from the Kuban Science Foundation within the framework of the research and innovative project no. NIP–20.1/135 “Design and Study of a Planetary Transmission with Elliptical Gears as Part of a Piston Compressor Drive”.

Введение. Механизмы с некруглыми зубчатыми колесами известны давно, однако их экспериментальные исследования и практическое внедрение долгое время были затруднены из-за узкой специализации таких механизмов, сложности и высокой стоимости их изготовления. В настоящий момент наблюдается повышение интереса исследователей к данной тематике. При этом большинство научных работ в области проектирования передач некруглыми зубчатыми колесами основано на анализе геометрии [1] и кинематики [2] с целью получения требуемой передаточной функции для практического применения [3] . В [4] и [5] разработаны и изучены механизмы для синтеза функций угловой скорости; исследователями предложена робототехника с некруглыми колесами, например, прыгающий робот [6] , робот-гексапод [7] , механизм экзоскелета для реабилитации коленного сустава [8] ; исследованы с точки зрения кинематики [9] и динамики [10] более эффективные посадочные машины для сельскохозяйственной промышленности; разработаны и спроектированы многие другие устройства.

Обзор источников показал, что наиболее распространены зубчатые колеса с эллиптической центроидой [11, 12] . Созданы машины [10] и устройства [4] с эллиптическими колесами, изучена геометрия [13] , решены некоторые вопросы проектирования [14] и изготовления [15] .

Эллиптические зубчатые колеса в основном применяются с целью передачи вращательного движения между параллельными неподвижными осями [16] . Однако такое использование некруглых колес позволяет получить лишь одностороннее неравномерное вращательное движение, что ограничивает сферу их применения. Планетарные передачи обладают более широкими возможностями для реализации сложных видов движения рабочих органов, а создание приводов на их основе позволит разработать и внедрить более эффективные и компактные машины различного технологического назначения.

По результатам анализа научной литературы в области передач некруглыми зубчатыми колесами в качестве объекта исследования предлагается планетарный механизм с эллиптическими колесами. Цель работы состоит в экспериментальном кинематическом анализе планетарной передачи и обосновывается необходимостью верификации теоретических положений для их корректного использования на следующих этапах проектирования — при динамическом, силовом анализе и расчетах на прочность.

Материалы и методы. Кинематическая модель механизма строится на основе плана скоростей его звеньев (рис. 1).

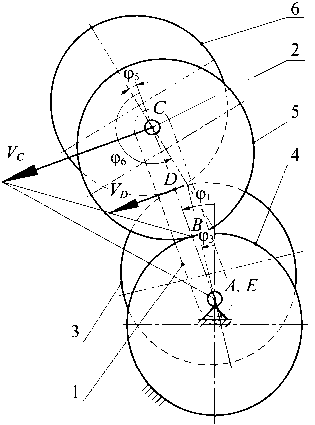
Рис. 1. План скоростей для рассматриваемого механизма:

1 — водило; 2 — вал сателлита; 3 — эллиптическое колесо на выходном валу; 4 — солнечное эллиптическое колесо; 5, 6 — эллиптические колеса сателлита

Аналог угловой скорости выходного вала определяется следующим образом [17] :

ю 3 _ V D ■ AC _ BD • AC ® ! = V C ■ DE ~ BC • DE'

Отрезки BD, BC и DE определяются через полярное уравнение эллипса [17] :

р(ф)_

a (1 - e2)

1 - e • cos ф

где φ — угол поворота; e и a — эксцентриситет и большая полуось эллипса.

Определим радиусы зацепления колес 5 и 6:

BC = P5 =

CD = P 6 =

a ( 1 — e 1 ² )

1 — e1 ■ cos ф5 a (1 — e 2)

1 - e 2 ■ cos ф6

где e 1 и e2 — эксцентриситеты для каждой пары эллиптических колес, углы поворота которых р ₅ и р ₆ получены следующим образом:

» 5 = |

^{1 -} e i2

1 + e l + 2 e 1 ■ cos ф 1

d Ф 1 .

Фб =П + Ф5.

Опираясь на план скоростей и учитывая уравнения (3), (4), определим искомые отрезки как:

BD = Р 6 —P 5 ,

AC = EC = 2 a , DE = 2 a — p 6 .

Опираясь на (2)–(9), получим выражение для определения аналога угловой скорости выходного вала:

,    (P6 —P5 )■ 2a

Ф з =--^---- V

P5 (2a — P6)

Угол поворота определяется интегрированием уравнения (10) по обобщенной координате р 1 :

Ф з = | ф з d Ф 1 .

Вариациями кинематической схемы механизма является замена эллиптических колес на цилиндрические в одной из пар, для исследования которых необходимо в полученной математической модели функции радиусов заменить на фиксированные значения.

Рассмотрим механизмы с парой эллиптических колес 3–6 ( e = 0,28), и цилиндрическими колесами 4 и 5 следующих размеров:

—

—

—

вариант 1: R 5 = 25 мм, R 4 = 25 мм;

вариант 2: R 5 = 18 мм, R 4 = 32 мм;

вариант 3: R 5 = 16 мм, R 4 = 34 мм.

На рис. 2 показаны графики функций положения, полученные с использованием (11).

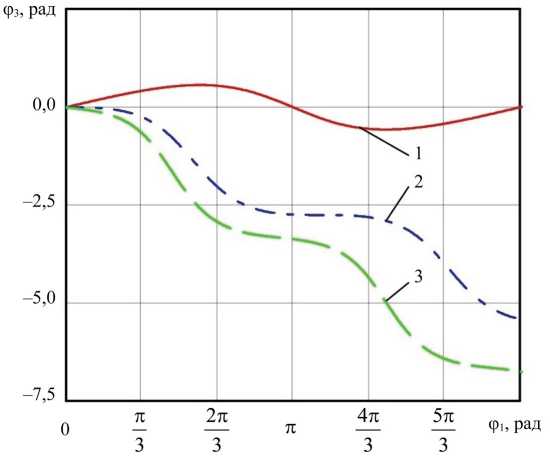
Рис. 2. Графики зависимостей для исследуемых конфигураций механизма

Анализ графиков показывает (на рис. 2 цифрами обозначены исследуемые варианты), что изменение размеров зубчатых колес позволяет получить различные виды движения выходного вала: возвратно-вращательное (вариант 1), прерывистое (вариант 2) и одностороннее неравномерное вращательное движение (вариант 3).

Машиностроение и машиноведение

Результаты исследования. Анализ кинематики подтвердил реализацию различных передаточных функций, а изменение размеров зубчатых колес позволяет проводить кинематический синтез новых механизмов.

Объектом экспериментального исследования служит прототип, детали которого показаны на рис. 3.

Рис. 3. Детали исследуемого прототипа

Углы поворота измеряются абсолютными энкодерами (таблица 1).

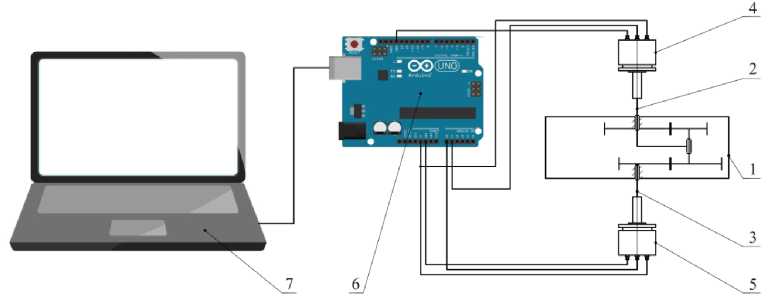
Рис. 4. Принципиальная схема ( а ) и внешний вид ( б ) экспериментального стенда:

1 — корпус; 2 — входной вал; 3 — выходной вал; 4, 5 — энкодеры; 6 — контроллер Arduino; 7 — персональный компьютер

Характеристики энкодеров

Таблица 1

Диаметр	Выходной сигнал	Разрешение	Линейность	Скорость чтения
22 мм	0–5 В	360°/ 4096 ≈ 0,088°	0,3 %	0,6 мс

Сигнал регистрируется контроллером Arduino и обрабатывается на ПК (рис. 4).

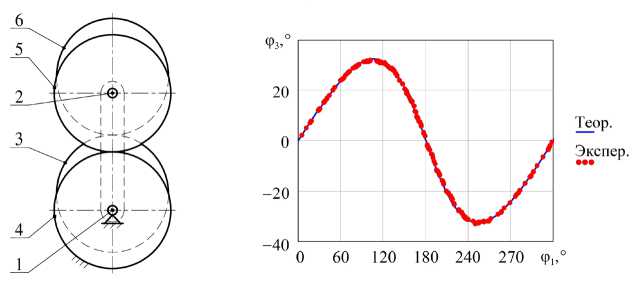
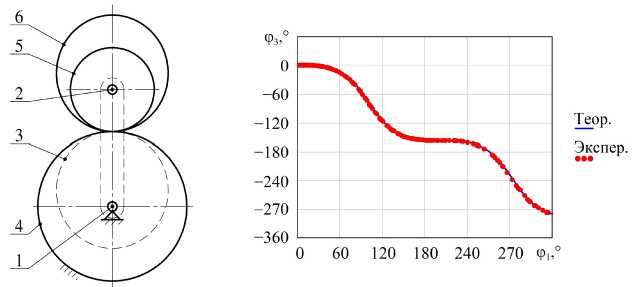
Обработка и анализ результатов измерений осуществлялись в прикладном пакете MathCAD. Схемы исследуемых вариантов и результаты эксперимента показаны на рис. 5. φ 3 ,°.

а)

б)

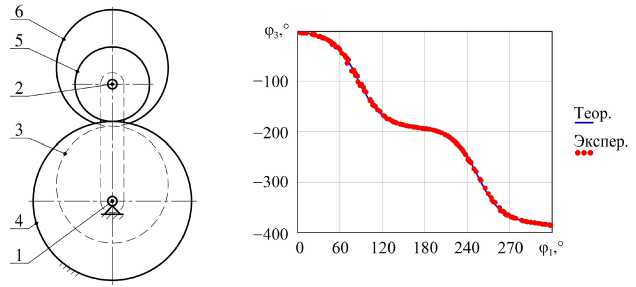
в)

Рис. 5. Результаты исследования: а — вариант 1; б — вариант 2; в — вариант 3

Как видно из графиков, измеренные значения углов поворота выходного вала адекватны построенной модели.

Оценим результаты эксперимента инструментами статистического анализа.

Определим среднее значение ошибок измерения [18] :

n q = -       qk,(12)

П ‘—‘k = 1

где n — количество независимых наблюдений q k .

Вычислим выборочную дисперсию:

s 2 (Qk ) =     S k=1 (qk - q ^ 2.

Оценку дисперсии среднего значения получим следующим образом:

s2 (q) = stlqkl.(14)

Стандартная неопределенность измерений по типу А определится [19] :

u (q ) = 7 s2 (q).

Машиностроение и машиноведение

Принимая за значения q k ошибки измерения и обрабатывая их согласно (12)–(15), вычислим неопределенность измерения. Результаты статистического анализа приведены в таблице 2.

Статистический анализ ошибок измерения

Таблица 2

Номер механизма	Количество измеренных значений	Среднее значение ошибки	Неопределенность измерения
1	195	–0,16°	0,04°
2	168	0,57°	0,11°
3	192	0,08°	0,13°

Доверительный интервал определяется как q ± 2 u для уровня достоверности 95 % и составляет –0,16 ± 0,08 (вариант 1), 0,57 ± 0,22 (вариант 2), 0,08 ± 0,26 (вариант 3). Таким образом, построенная математическая модель кинематики адекватна физическим прототипам.

Обсуждение и заключение. Представлена планетарная передача с эллиптическими колесами, позволяющая реализовать неравномерное, прерывистое и возвратно-вращательное движение выходного вала. Вид движения определяется параметрами зубчатых колес.

Построена кинематическая модель передачи, получен закон движения выходного вала. Анализ механизмов с различными параметрами зубчатых колес показал реализуемость широкого спектра передаточных функций и видов движения выходного вала.

Соответствие результатов проведенного кинематического анализа реальным механизмам подтверждено экспериментальным исследованием функций положения выходного вала для трех вариантов физического прототипа. Проведенная оценка адекватности математической модели позволяет использовать ее при динамическом и силовом анализе машин на базе предлагаемых передач. Исследуемые варианты механизма могут применяться в приводах компактных и простых в уравновешивании технологических машин.