Экспериментальное исследование модели покрытия ледового дворца в г. Челябинске

В.Ф. Сабуров, Ю.А. Ивашенко, Н.Б. Козьмин, Н.В. Гусева

В статье приведены методика и результаты экспериментального исследования модели, изготовленной в масштабе 1:10 реальной конструкции покрытия ледового дворца.

Крытый ледовый дворец «Уральская молния» представляет собой одноэтажное здание длиной 198 м, пролетом 84 м с консолями по 4,3 м. Его несущая конструкция - поперечная рама, образованная двухветвевыми колоннами и ригелем в виде пологого криволинейного бруса (арки), подкрепленного шпренгелем ломаного очертания. Арка покрытия состоит из прямолинейных сегментов длиной 8,4 м, соединенных между собой фланцами на высокопрочных болтах. Пролет арки L_K = 83,4 м; радиус нейтральной линии R_H = 206 700 мм; стрела подъема арки /= 4250 мм. Общий вид конструкции покрытия с указанием сечения конструктивных элементов показан на рис. 1.

Данное конструктивное решение покрытий большепролетных зданий редко применяется в практике строительства. В России известны два объекта: покрытие малой спортивной арены в Лужниках пролетом 72 м [1]; покрытие Гостиного Двора с максимальным пролетом 80,74 м [2]. Из этого следует, что конструкция в виде пологой арки, подкрепленной ломаным шпренгелем, при всей простоте конструктивной формы является мало исследованной. Поскольку в технической литературе отсутствует методика расчета криволинейного бруса со шпренгелем как единой систе мы, а также не достаточно освещен вопрос о влиянии податливости болтовых соединений на прочность и устойчивость конструкции в целом, то для выявления действительной работы конструкции и оценки её пригодности к эксплуатации потребовалось провести экспериментальное исследование её модели.

Моделирование сечений арки и шпренгеля выполнено по методу приближенного геометрического подобия [3]. При моделировании принято, что коэффициент Пуассона и модуль упругости материала модели и натурной конструкции равны, перемещения модели и натуры идентичны, а относительные деформации в несущих элементах модели и натурной конструкции при упругой работе материала одинаковы. Фланцевые болтовые соединения при моделировании не учитывались. Масштаб геометрического подобия принят равным т = 0,1.

Таким образом, в соответствии с предпосылками, имеем индикаторы подобия:

- — ^£м —      — Rm —1. Р _ ^М _ 1

А ~---1, Ц_г---Ь_Т- — -1.

A        At        ^н

Для определения относительной деформации sH выполнен расчет поперечного сечения арки натурной конструкции. Из условия прочности сечения

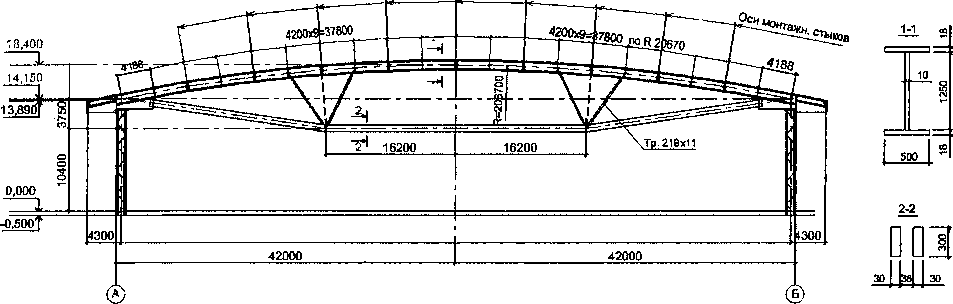
Рис. 1. Схема поперечной рамы крытого ледового дворца

арки, устойчивости дуги арки между У-образными раскосами, а также из условия прочности шпренгеля относительные деформации составили сн = 0,0012. С учетом разницы расчетных сопротивлений материалов натуры и модели равенство относительных деформаций имеет вид:

£н^ум = ^м^ун ’ и, следовательно,

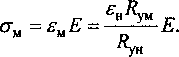
Из расчета модели покрытия при узловой нагрузке на арку 100 кг наибольшее усилие в шпрен-геле составило Ам = 2512 кг, наибольшее усилие в арке N = -2561 кг, М = 57 кгм . Требуемая пло щадь поперечного сечения шпренгеля составила

NJ^ 2512-3050      . , .

----— =-----------;-----= 1,24 см е^Е 0,0012-2,НО⁶-2450

По конструктивным соображениям площадь поперечного сечения шпренгеля принята равной 4 см2 (полоса 8x0,5 см). При данной площади сечения шпренгеля для равенства деформаций нагрузка на узел должна составлять 320 кг, а усилие в шпренгеле при этом равно NM = 8 т. Относи тельная деформация шпренгеля ем = 8000/2,1-106-4 = 0,001.

При узловой нагрузке Р = 320 кг усилия в арке составили

N_M= -2,561-3,2=-8,2 т, М_м = 0,057-3,2 = 0,184 тм, где 3,2 = 4/1,24 - отношение фактической площади шпренгеля к требуемой при Р = 100 кг. Исходя из данных усилий подобрано сечение арки в виде двутавра с толщиной полок 3 мм (рис. 2). Из условия местной устойчивости сжатого свеса полки определена ширина пояса, равная 60 мм. Момент инерции сечения J_x = 108 см⁴, момент сопротивления %=20,4 см³, площадь сечения Л_м= 5,1 см².

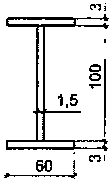
Рис. 2. Сечение модели арки

Напряжение

N_M М_м 8200 18 400

^м 4, W_x 5,1    20,4

= 1608+ 902 = 2510 кг/см2, откуда ем = 0,0012 = ен.

Сечение V-образных раскосов принято из труб 22x2 мм.

Таким образом, модель конструкции покрытия разработана с соблюдением следующих принципов: основные габаритные размеры (длина, высота, стрела подъема арки) геометрически подобны в масштабе 1:10 натурной конструкции; сечения арки и шпренгеля назначены из условия равенства относительных деформаций модели и натурной конструкции.

Изготовлены две модели арки, сегменты которых длиной 840 мм соединены на фланцах болтами диаметром 10 мм класса прочности 5.8, поставленными в отверстия такого же размера. Каждая арка соединена со шпренгелем телескопическими раскосами с резьбовыми упорами, позволяющими менять их длину. Дм обеспечения устойчивости арок из плоскости собран и испытан блок из двух арок, соединенных прогонами, горизонтальными связями по верхним поясам и вертикальными - в зоне установки раскосов (как в реальной конструкции).

Предварительно дм оценки общей жесткости конструкции было произведено смещение кривого бруса относительно шпренгеля с помощью телескопических соединений раскосов; при этом измеряли продольную деформацию верхней полки арки в зоне сплошного сечения и в зоне фланца (рис. 3). Измерение деформаций проводили с помощью тензометров Аистова с базой 50 мм. Получены следующие значения приращений деформаций (усредненные по результатам нескольких испытаний): по показаниям Т-1 Ас = 18, по показаниям Т-2 Ас = 2. Расстояние между тензометрами Т-1 и Т-2 составмет 100 мм.

Дм изгибаемых элементов угол поворота сечения в = М/В, где М - изгибающий момент, В - погонная изгиб-ная жесткость.

В месте расположения тензометров Т-1 и Т-2 принимаем, что М= const, и тогда отношение жест-

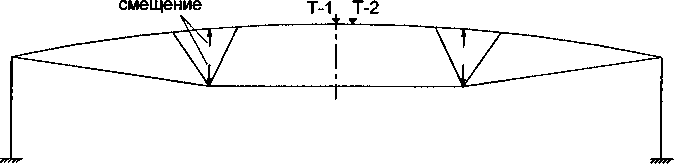
Рис. 3. Схема размещения приборов при создании смещения арки и шпренгеля

костей сплошного сечения и фланцевого соединения равно вс[в^=9^ес.

Анализ деформативности системы кривой брус-шпренгель показал, что угол поворота для сплошного сечения составил (рис. 4, а):

е„ = tga = ——=—=—=0,019, ^{с с} 2-0,5А 20,5106

а для фланцевого соединения при условии, что поворот происходит по оси нижнего болта (рис. 4, б), равен

^stg^=18/(2-78) = 0,115.

Отношение

Д/5ф =0,115/0,019 = 6,05, следовательно, жесткость фланцевого соединения в коньке в 6 раз меньше, чем целого сечения.

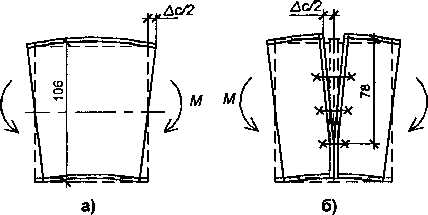
Рис. 4. Поворот сечения при изгибе: а - сплошного сечения; б - болтового соединения

В программе «Лира-9.2» выполнен расчет модели покрытия на симметричную и несимметричную вертикальную нагрузки. На рис. 5 показана схема нагружения конструкции равномерной нагрузкой, приведены эпюры продольных сил и изгибающих моментов. В таблице даны значения внутренних усилий для натурной конструкции и для модели при расчетных равномерных нагрузках. В соответствии с данными эпюрами выполнена расстановка приборов в сечениях модели, где возникают наибольшие внутренние усилия (рис. 7).

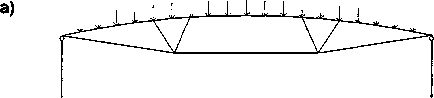
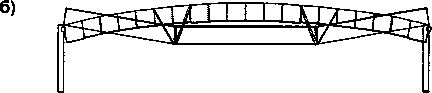
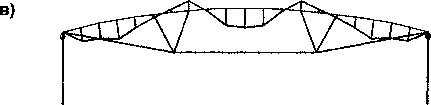
Рис. 5. Нагружение симметричной нагрузкой: а - схема нагружения; б - эпюра продольных сил; в - эпюра изгибающих моментов

Таблица

Зона	Натурная конструкция		Модель
	N, т	М, тм	N, т	М, тм
Сеч. 1; 7	-474,7	60,95	-7,37	0,19
Сеч. 2; 6	-474,7	14,26	-7,30	0,05
Сеч. 3; 5	-488,2	-41,54	-7,45	-0,07
Сеч. 4; 4*	-486,8	48,40	-7,42	0,17
Сеч. 8; 11	-21,2	—	-0,39	—
Сеч. 9; 10	-54,1	—	-0,83	—
Сеч. 12; 14	480,6	—	7,35	—
Сеч. 13	488,6	—	7,41	—

Примечание. Расположение сечений с приборами показано на рис. 7, а.

Для проведения эксперимента была разработана оснастка (рис. 6), которая позволила произвести нагружение, соответствующее нагружению натурной конструкции.

Рис. 6. Блок арок с оснасткой при испытании

Перемещения кривого бруса измерялись про-гибомерами на базе индикатора часового типа с ценой деления 0,1 мм (рис. 7, б), а деформации -тензометрами Аистова с базой 50 мм и проволочными тензорезисторами с базой 20 мм (рис. 7, в, г). Регистрация показаний тензодатчиков осуществлялась тензометрическим комплексом СИИТ-3.

Вертикальная нагрузка прикладывалась по кривому брусу в 19 сечениях в местах расположения прогонов. Нагрузка создавалась путем укладки гирь средним весом 20,44 кг на платформы и через распределительные элементы передавалась в узлы. Для центровки в местах передачи нагрузки на кривой брус были установлены шаровые опоры (рис. 7, б, г).

Загружение конструкции производилось в 12 этапов: на первых 9 этапах создавалось симметричное загружение равномерной нагрузкой с приращением нагрузки в узел арки на 30 кг, на 10, 11, 12-м этапах - несимметричное нагружение. Разрушение модели произошло на 12-м этапе.

Для анализа результатов испытаний рассмотрены следующие сечения: на арке - сечение 2 и 3 в зоне узлов примыкания раскосов к арке, сечение 4а в коньковом узле, где возникают максимальные перемещения арки, сечение 7 в опорной зоне арки

б)

В)

Рис. 7. Расстановка измерительных приборов: а - схема; б - тензодатчики и прогибомер на арке; в - тензодатчики и тензометр на шпренгеле; г - тензодатчики и тензометр на арке

Г)

с наибольшим положительным моментом; на шпренгеле - сечение 13; на раскосах - сечение 11. Для этих сечений построены зависимости на пряжений от нагрузки. В качестве примера на рис. 8 приведены зависимости для некоторых из перечисленных сечений. Из этих зависимостей видно

а)

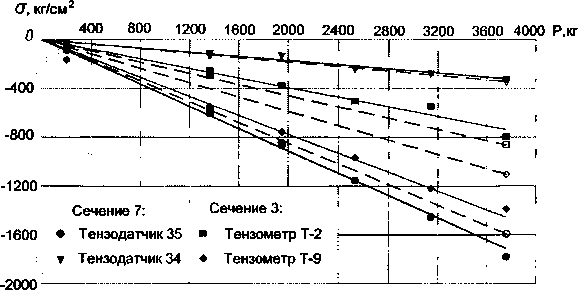
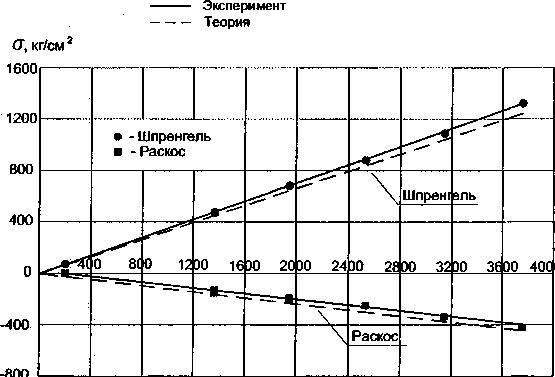
----- Эксперимент

--- Теория

Рис. 8. Зависимости напряжений от нагрузки: а - для сечений на арке; б - для сечений на шпренгеле и раскосах

(рис. 8, а), что на всех этапах нагружения рост напряжений в сечениях арки происходит пропорционально увеличению нагрузки, что свидетельствует об упругой работе модели. Однако для отдельных сечений наблюдается увеличение напряжений по сравнению с теоретическими, причем разница между теорией и экспериментом растет с каждым этапом нагружения и составляет от 3-10 % на начальных этапах до 7-48 % на 9-м этапе. В элементах, испытывающих осевые усилия (шпренгель и раскосы) и не имеющих фланцевых соединений, расхождение между экспериментом и теорией незначительно и составляет не более 5 % (рис. 8, б). Это свидетельствует о влиянии податливости флан цевого соединения модели на ее напряженное состояние.

На рис. 9 приведены эпюры напряжений по сечениям арки при наибольшей симметричной нагрузке (9 этап) и при нагружении несимметричной нагрузкой (12 этап). Здесь же даны конструктивные поправки, равные отношению экспериментальных напряжений к теоретическим. Видно, что наблюдается непропорциональное увеличение напряжений в кривом брусе. Особенно сильная непропорциональность проявилась в зонах примыкания раскосов в сечениях 2 и 3 на 12-м этапе нагружения.

На рис. 10 представлена зависимость перемещений сечений 2 и 4 от симметричной нагрузки.

9 этап         9 этап 12 этап

(эксп-т) (теория) (эксп-т)

12 этап (теория)

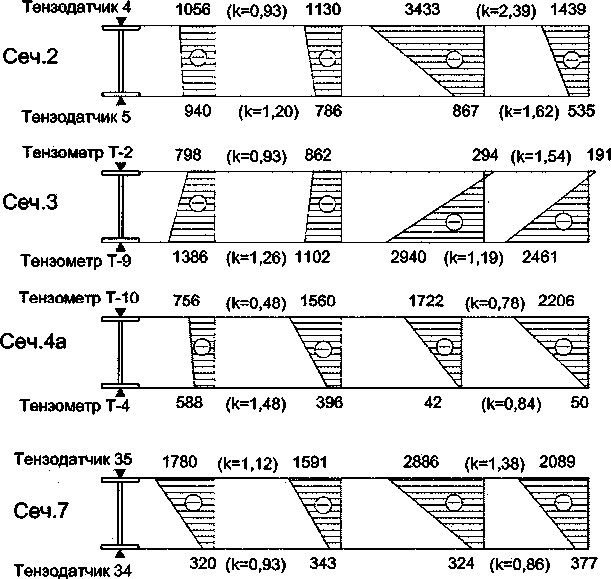
Рис. 9. Эпюры напряжений по сечениям арки, кг/см2

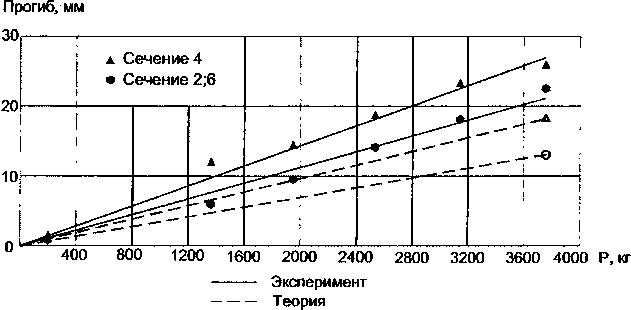
Рис. 10. Зависимости перемещений арки от нагрузки

Из рисунка видно, что экспериментальные прогибы арки превышают теоретическое значение от 11 % на начальном этапе до 72 % на последнем этапе приложения равномерной нагрузки. Это расхождение может быть вызвано податливостью фланцевых соединений сегментов арки.

По результатам эксперимента можно сделать вывод о снижении жесткости кривого бруса модели при действии вертикальной нагрузки из-за наличия фланцевых соединений его сегментов.