Экспериментальное исследование обратимого алгоритма сокрытия данных в зашифрованных изображениях на основе использования кода Хэмминга (7,4) и MSB-прогнозирования

На сегодняшний день известен и исследован ряд методов обратимого сокрытия данных, которые работают с изображениями. В основном эти методы используют расширение разницы (DE) [7], сдвиг гистограммы (HS) [8], упорядочивание значений пикселей (PVO) [3; 6] и модификацию ошибок прогнозирования [2; 4; 5]. Все эти методы учитывают пространственную корреляцию и избыточность изображений для встраивания дополнительных битов.

Алгоритм, рассматриваемый в данной работе, был представлен китайскими учеными Каймен Ченом (Kaimeng Chen) и Чин-Чен Чангом (Chin-Chen Chang) в статье [4]. Он основан на кодировании по Хэммингу (7,4) и MSB-прогнозировании.

Экспериментальное исследование обратимого алгоритма сокрытия данных ...

Бахрушина Галина Ивановна кандидат физико-математических наук, доцент, доцент кафедры программного обеспечения вычислительной техники и автоматизированных систем. Тихоокеанский государственный университет, город Хабаровск. Сфера научных интересов: информационные технологии; разработка программного обеспечения; цифровое маркирование изображений. Автор более 70 опубликованных научных работ.

Ранее авторами была подготовлена и опубликована статья [1] с детальным описанием вышеуказанного алгоритма, реализованного на языке C#. В настоящей статье приводятся результаты экспериментального исследования алгоритма.

Метрики, позволяющие измерять эффективность алгоритма

Для измерения эффективности алгоритма в работе использовались такие известные метрики, как PSNR, NC и BPP.

Пиковое отношение сигнала к шуму (PSNR). PSNR (Peak Signalto Noise Ratio) используется для измерения уровня искажений при работе с изображениями. PSNR отражает соотношение между максимумом возможного значения сигнала и мощностью шума, искажающего значение сигнала. Обычно измеряется в децибелах (при полном совпадении изображений PSNR стремится к бесконечности). Для его определения используется среднеквадратичная ошибка MSE (Mean Square Error).

Для двух изображений I и K размером m×n, одно из которых считается зашумленным приближением другого, MSE вычисляется по формуле m-ivi n-12

MS=—Х-Х,-0J(i,j)-K(i,j) ;(1)

mn^^i = 0 *-^j - 0¹

PSNR определяется по формуле

( MAX 2 )

PSNR = 10log        I ,(2)

• ¹⁰ ( MSE J

где MAX_I = 255 для разрядности 8 бит или максимальному значению, принимаемому пикселем изображения, – в противном случае.

Считается, что человеческий глаз практически не различает искажений при PSNR >  35 дБ .

Коэффициент нормированной взаимной корреляции (NС). NС используется в качестве меры идентичности исходного и маркированного изображения или для сравнения внедренной и извлеченной информации.

Для двух изображений I и K размером m × n NC вычисляется по формуле

NC =

z moz ni (i- j) к (i,j)

/x^ m ly^. n ^-1 ,   .2 ^-i m -1^4 n -1  z. .,2

V L , =o z j =o ^{1 (} i , j ) z , =o z j =o K ⁽ i , j )

Значения коэффициента находятся в диапазоне [0, 1]. Чем ближе коэффициент к единице, тем больше сходство между сравниваемыми изображениями (при полном совпадении изображений NC равно единице).

Порог внедрения (ER). ER (Embedding Rate) – максимальное количество бит, которое можно внедрить в один пиксель изображения с помощью рассматриваемого алгоритма. Рассчитывается как отношение максимально возможного объема внедрения в изображение к общему числу пикселей изображения. Единица измерения – количество бит на пиксель, или bpp (bit per pixel). Для данного алгоритма порог внедрения определяется по формуле

3 ( m- 2 ⁾⁽ n — 2 ) ER = • --------------,

7 mn

где m и n – размеры изображения.

Результаты экспериментальных исследований

Для экспериментальных исследований было выбрано 15 изображений разных размеров (Grapes, Lynx и Safari размером 128×128 пикселей, Cameraman, Bird, Barbara – 256×256, Baboon, Lena, Jet – 512×512, Road, Car, Leopard – 800×600, Boeing, Smoke, Good Day – 1000×1000).

Были изучены следующие зависимости:

• –    качество внедрения короткого и длинного сообщения от размера изображений;

• –    значение порога внедрения от размера изображения.

Зависимость качества внедрения длинного сообщения от размера изображений. На Рисунках 1, 2 представлены исходные и маркированные изображения Grapes, Lynx и Safari размером 128×128 пикселей, а в Таблице 1 отражены значения метрик PSNR и NC между исходными и соответствующими маркированными изображениями для случая внедрения длинного сообщения. Длинное сообщение считывается из текстового файла (см. Рисунок 3).

Рисунок 1. Исходные изображения размером 128×128

Экспериментальное исследование обратимого алгоритма сокрытия данных ...

Рисунок 2. Маркированные изображения размером 128×128 с внедренным длинным сообщением

Таблица 1

Значения метрик PSNR и NC при внедрении длинного сообщения для изображений размером 128×128

Изображение	PSNR	NC
Grapes	46,4027069396312	0,999955883479634
Lynx	50,9078554195244	0,999970363034833
Safari	50,9274942550007	0,999981930509711
Среднее значение	49,4126855380521	0,999969392341393

В Таблицах 2–5 приведены значения метрик PSNR и NC для исходных и соответствующих им маркированных изображений остальных фиксированных размеров при внедрении длинного сообщения, а также их средние значения.

Таблица 2

Значения метрик PSNR и NC при внедрении длинного сообщения для изображений размером 256×256

Изображение	PSNR	NC
Bird	50,8130603552931	0,999983178209008
Cameraman	46,2522171826809	0,999957147093394
Barbara	44,5285277171326	0,999912319764618
Среднее значение	47,1979350850355	0,999950881689007

Таблица 3

Значения метрик PSNR и NC при внедрении длинного сообщения для изображений размером 512×512

Изображение	PSNR	NC
Baboon	48,8691370155287	0,999978767213198
Lena	50,7906899463369	0,999984670519845
Jet	50,8102654203584	0,999992211553999
Среднее значение	50,1566974607413	0,999985216429014

Таблица 4

Значения метрик PSNR и NC при внедрении длинного сообщения для изображений размером 800×600

Изображение	PSNR	NC
Road	50,5264531123524	0,999983509465575
Car	45,4008487943587	0,999949281192931
Leopard	48,2014871202226	0,999954377327815
Среднее значение	48,0429296756446	0,999962389328774

Таблица 5

Значения метрик PSNR и NC при внедрении длинного сообщения для изображений размером 1000×1000

Изображение	PSNR	NC
Boeing	47,8585351470399	0,999976216816141
Smoke	48,4735810088247	0,999917503500045
GoodDay	50,7789359775193	0,999982467304119
Среднее значение	49,0370173777946	0,999958729206768

На Рисунках 4, 5 представлены графики зависимости значения метрик PSNR и NC соответственно, построенные по средним значениям из Таблиц 1–5.

Экспериментальное исследование обратимого алгоритма сокрытия данных ...

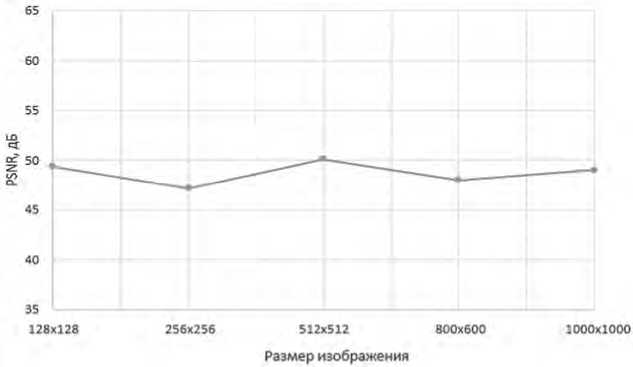
Рисунок 4. График зависимости значения метрики PSNR от размеров изображений при внедрении длинного сообщения

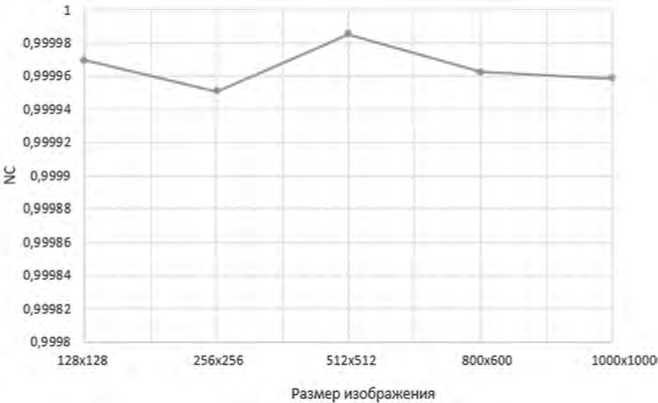
Рисунок 5. График зависимости значения метрики NC от размеров изображений при внедрении длинного сообщения

Установлено, что значения PSNR колеблются в пределах примерно от 45 до 50 дБ, что является хорошим показателем. Во всех случаях разница изображений незаметна для глаз. Значения NC приближены к единице, следовательно, изображения очень похожи. В целом зависимость значений метрик от размера изображения выражена очень слабо – практически не просматривается (наблюдаются лишь небольшие колебания значений метрик). Возможно, получить более точный результат удалось бы при наборе большей статистики.

Внедрение короткого сообщения. Аналогичные исследования были выполнены для случая внедрения короткого сообщения. Короткое сообщение задается в программе строкой Hello, World! При внедрении короткого сообщения показатели качества внедре- ния несколько выше – значение PSNR колеблется в пределах примерно от 55 до 60 дБ, а значения NC либо равны единице, либо близки к ней. Зависимость значений метрик от размера изображения также слабо выражена (но показатели несколько выше для изображений небольшого размера).

Зависимость значения порога внедрения от размера изображения. Для расчета порога внедрения использовалась формула (4). В Таблице 6 приведены данные расчета порога внедрения для изображений разных размеров.

Таблица 6

Данные расчета порога внедрения для изображений разных размеров

Размер изображения	Порог внедрения
128×128	0,415283203
256×256	0,421890259
512×512	0,425228119
800×600	0,426075000
1000×1000	0,426858000

На Рисунке 6 представлен график зависимости порога внедрения от размера изображения.

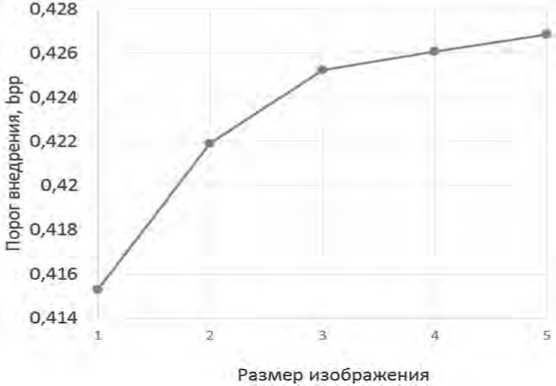
Рисунок 6. График зависимости порога внедрения от размера изображения: 1 – изображение размером 128×128; 2 – 256×256; 3 – 512×512; 4 – 800×600; 5 – 1000×1000

Из графика видно, что порог внедрения ER растет при увеличении размера изображения. Это можно объяснить тем, что при увеличении размера изображения растет число модифицируемых пикселей.

Заключение

Рассмотренный алгоритм был реализован на языке программирования C# в среде разработки Microsoft Visual Studio 2019 и исследован на обратимость, качество встраивания и извлечения информации. С помощью разработанной программы была исследована за-

Экспериментальное исследование обратимого алгоритма сокрытия данных ...

висимость основных метрик, характеризующих эффективность алгоритма (PSNR и NC), а также порога внедрения (ER) от размера изображения. При этом рассматривались короткие и длинные внедряемые сообщения.

При выполнении экспериментальных исследований было установлено, что PSNR между исходным и маркированным изображениями находится на высоком уровне (от 45 до 60 дБ).