Экспериментальное исследование остаточной влажности кожи

DOI:

Основной задачей процесса валкового отжима кожевенного полуфабриката после хромового дубления (кожи) является обеспечение требуемой технологическим процессом остаточной влажности. Поэтому при валковом отжиме кожи одной из основных задач является определение аналитической зависимости остаточной влажности от основных параметров процесса валкового отжима, то есть необходимо моделирование остаточной влажности кожи.

В теории валкового отжима кожи исследования по моделированию остаточной влажности отжимаемого материала проводятся в трех направлениях. Первое ‒ экспериментальное, строится на основе опытных данных с применением методов математической статистики и планирования эксперимента, результаты получаются в виде эмпирических или регрессионных зависимостей. Второе ‒ экспериментальнотеоретическое, строится путем теоретических исследований на основе экспериментально полученных эмпирических зависимостей. Третье - теоретическое, строится на основе теоретических исследований путем изучения гидравлических явлений, происходящих в зоне контакта валков с отжимаемым материалом.

Работы [1-3] посвящены экспериментальному исследованию и описанию регрессионной модели остаточной влажности кожевенного полуфабриката с вертикальной подачей.

Данная работа посвящена экспериментальному исследованию и моделированию остаточной влажности кожи с горизонтальной подачей.

МЕТОДЫ

Экспериментальные исследования проводились на специально спроектированной и изготовленной установке (рис. 1).

Для выполнения экспериментальных работ предусмотрен комплект валков с различными диаметрами. Конструкция установки позволяет заменять валки, а также изменять скорость вращения валков и усилия их прижима. Были изготовлены валки с диаметрами 0,1, 0,21 и 0,326 м . После намотки, диаметры валков равнялись 0,116, 0,228 и 0,340 м. Длина валков во всех случаях составляла 0,12 м . Скорости вращения валков регулируются с помощью реостатов и измеряются тахометром часового типа. Диапазон изменения интенсивности нагрузки  15 – 65 кН / м.

Необходимое давление валков создавалось собственным весом верхнего валка и усилием дополнительного прижима, осуществляемым с помощью пружинно-винтовой системы.

Рисунок 1. Вид экспериментальной установки.

• Figure 1. View of the experimental setup.

Для определения остаточной влажности в каждом отжатом образце кожи проводили пять замеров процентного содержания влаги по углам и середине образца. Средняя арифметическая величина этих замеров составляла остаточную влажность образца. При измерении влажности применяли сушильный шкаф СНОЛ -2,5; весы типа ВЛР-200 с точностью измерения 0,01 мг, эксикаторы, бюксы.

Исследованию подвергались кожевенные полуфабрикаты крупного рогатого скота после хромового дубления. Образцы вырезали из кожевенных полуфабрикатов шириной 0,2 м и требуемой длиной в зависимости от вида опытов. Укомплектовали образцы с целью исключения влияния топографических различий в группы по методу асимметрической бахромы.

В качестве функции отклика принимали W , которая полностью отвечает требованиям, предъявляемым к функциям отклика при планировании эксперимента [4].

На основе поисковых экспериментов было принято решение проводить экспериментальное исследование методом D-оптимального планирования второго порядка с использованием матрицы планирования К. Кано.

На основе априорной информации W исследование проводилось с учетом трех факторов: x_t — интенсивность нагрузки Q , кН / м; х₂ — диаметр валка D , м; х₃ — скорость валка V , м / с.

Выбраны следующие диапазоны изменения факторов: интенсивность нагрузки – 15 ^ 65 кН / м ; -диаметр валка - 0,116, 0,228, 0,340 м ; скорость валка - 0,10 ^ 0,34 м / с.

• Уровни и интервалы варьирования факторов приведены в таблице 1.

Таблица 1. Уровни и интервалы варьирования факторов.

Table 1. Levels and intervals of factor variation.

Фактор	Уровень варьирования			Интервал вариации
	-	0	+
Q , кН / м	15	40	65	25
Qx	0,375	1,000	1,625	0,625
D , м	0,116	0,228	0,340	0,112
D 1	0,509	1,000	1,491	0,491
V , м / c	0,10	0,22	0,34	0,12
V 1	0,454	1,000	1,546	0,546

Функция цели аппроксимирована полиномом kkk у 0 = b 0+E bx+E Мл+Е biixf, i=1               i, j =1

где b ₀, b , b , b_u — коэффициенты регрессии.

После реализации рабочей матрицы получено среднее арифметическое значение W _ост (таблица 2).

Однородность дисперсий оценена критерием Фишера [4] при доверительной вероятности a = 0,95 :

S ²

Fpac4 = Tmax, SL = 18,485; f.7 = 5; SL = 3,125; f6 = 4;  F,асч = 5,92.

min

Табличные значения критерия Фишера при f_maх = 5 и f _m^ = 4 равны F _Ta6л = 6,26 [4].

Таким образом, все дисперсии для W и N при a = 0,95 можно считать однородным, так как F < F , . ,                расч       табл

Таблица 2. Результаты экспериментального исследования.

Table 2. Results of the pilot study.

Рабочая матрица			Остаточная влажность		,2 _(W 0 - W 0 ) 2
					" i = V    W 0    )
Q 1	R 1	V 1	W 0	W 0
1,000	1,000	1,000	57,93	57,13	0,0002
1,625	1,491	1,546	58,64	57,89	0,0001
1,625	0,509	1,546	56,32	55,10	0,0005
0,375	0,509	1,546	60,59	61,77	0,0004
0,375	1,491	1,546	62,09	64,90	0,0019
1,625	1,491	0,454	52,31	52,81	0,0000
1,625	0,509	0,454	43,51	50,26	0,0241
0,375	0,509	0,454	58,47	56,35	0,0000
0,375	1,491	0,454	60,24	59,20	0,0000
1,625	1,000	1,546	57,18	56,83	0,0000
1,000	0,509	1,546	59,63	57,22	0,0000
0,375	1,000	1,546	59,80	63,72	0,0043
1,625	0,509	1,000	54,13	53,32	0,0002
0,375	0,509	1,000	61,10	59,79	0,0000
0,375	1,491	1,000	61,17	62,82	0,0007
1,625	1,491	1,000	58,43	56,03	0,0017
1,000	1,491	1,546	59,38	60,12	0,0002
1,625	1,000	0,454	51,06	51,84	0,0002
1,000	0,509	0,454	53,52	52,20	0,0006
0,375	1,000	0,454	59,31	58,13	0,0000
1,000	1,491	0,454	57,26	54,84	0,0018
21 2 1			1202,07	1202,27	0,0370

После определения и исключения независимых коэффициентов регрессии плана К. Кано [4] получены уравнения:

W_ocт = 58,03 - 0,718 x 2 - 1,442 x ₃ ² + 0,529 x,x ₂ + 1,705 x,x₃ - 3,431 x_x + 0,776 x ₂ + 2,481 x₃ .  (2)

Гипотезу об адекватности найденных уравнений проверили с помощью критерия

Фишера [4] при доверительной вероятности а = 0,95 :

с 2            L n ( У и. - у . )²

ад         2         1

^расч = с 2,} , ^ад = _N   ( k + 1)( к + 2) ;

N

L si f-,

N

L s.

S2 = 16,577;  Sf,, = 11,434;  /   . = 1,45;  f„ = 11;  f„ = 91;

Табличные значения критерия Фишера при f_maх = 90 и f _m^ = 91 и f_m ^ = 11 равны F _Ta6л = 1,85 [4]. Таким образом, уравнение (2) можно считать пригодным с 95%-ной доверительной вероятностью ( F _pacч<  F_{ma бл}).

После раскодирования уравнения (2) получим

Wocт = 57,57 - 0,001102 - 100,4V2 + 0,377QD + 0,5680V - 0,256Q +12,5D + 42V.  (3)

При проектировании отжимных машин для инженерных расчетов требуются более простые зависимости. Исходя из этого, зависимости остаточной влажности от основных параметров отжима аппроксимируем степенной функцией.

Согласно методике, изложенной в работе [6], будем принимать степенную

зависимость вида

W o = CQ 1 ^a D 1 V ^Y ,

где

Q i = — , D = —, V = — . 111

ср                ср              ср

Логарифмирование (4) дает

In W = In C + a In Q ] + в ln D i + Y ln V .

Обозначив In W = Y , ln C = n , ln Q i = X i, ln D i = X 2 и ln V = X 3, приведем выражение (6)

к линейному виду

Y = aX_x + PX₃ + yX₃ + 9 .

Параметры а, в, у и n находим методом наименьших квадратов, согласно которой, сумма квадратов отклонений ^ экспериментальных точек от прямой должен быть

21        21

наименьшей, то есть F( а , в , у , п ) = 2 2 = 2 Y - ( а X i . + в Х 2 i + / X з i + П )) 2 — минимум.

i = 1           i = 1

Тогда имеем:

21             2121

а 2 X 2 + в 2 X 1 Х 2. + Y 2 X _UX з.

i=1                 i=1

21                  2121

а? XuXz i + в У X 22 + /У X2,X3, 1 i 2 i "          2 i     /          2 i 3 i i=1                         i=1

21                2121

аУ XhX3t + вУ X2/X3t + /2 XI 1i    3i                   2i    3i3

i=1                         i=1

21                  2121

+ n 2 X1 i =2 X uY., i=1

^{+ n} 2 ^X 2 i = 2 ^X 2 i^Yi ,

T1        2=1

+ n 2 X 3i=2 X 3.Y., i=1

а 2 X _{u +} в 2 X 2 . +    у 2 X з i +    21 n = 2 Y i .

i = 1                           i = 1                           i = 1                                    i = 1

После подстановки все суммы, получаем

9,582 а + 0,410 в + 0,526 / - 3,963 n = - 16,715, 0,410 а + 4,925 в + 0,293 / - 2,207 n = - 8,711,

0,526 а + 0,293 в + 6,507 / - 2,832 n = - 10,999, - 3,963 а - 2,207 в - 2,832 / +    21 n = 84,948.

Система (6) имеет решение: а = - 0,078 в = 0,046; у = 0,074; у = 0,074; n = 4,0454.

Отсюда, находим C = e ⁿ = e ^4,0454 = 57,63.

Таким образом, формула (4) будет иметь вид

W = 58,980!

-0,077Dx

0,046

V1

0,074

Вычисленные по формуле (10) значения остаточной влажности W приведены в таблице 2.

Определяем среднее квадратичное отклонение [5]

о

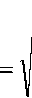
n

2 Y i=1

n - 2

0,0370 19

= 0,0441

и

коэффициент вариации

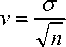
0,0441 21

= 0,0096.

Как видно, точность аппроксимации опытных данных формулой (7) более чем удовлетворительна.

РЕЗУЛЬТАТЫ

Из графы 4 таблицы 2 следует, что сумма остаточных влажностей в процессе экспериментального исследования равна 1202,07%. Отсюда, имеем W o _ср = 57,25% . С учетом этого из выражения (10) можно получить следующие зависимости

W = 0,97 2 1

- 0,077 d^

0,046

V1

0,074

W = 92,58 2

- 0,077р 0,046^ 0,074

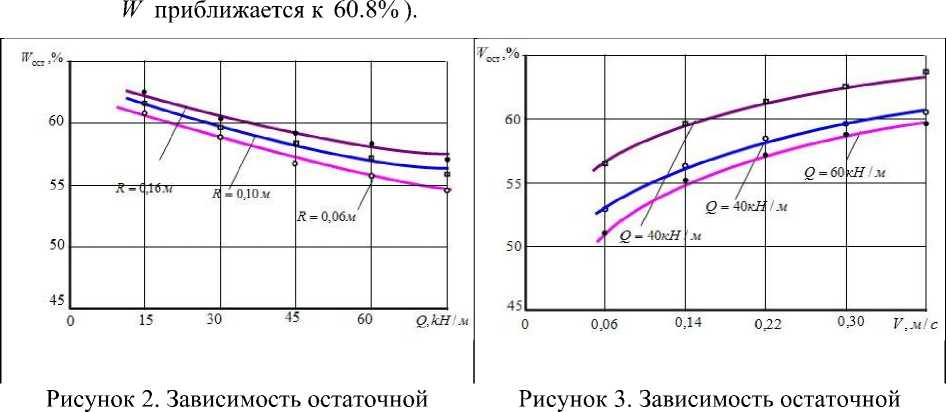
На рис. 2- 4 приведены графические интерпретации формулы (12).

ВЫВОДЫ

• 1.    Разработаны регрессионные и эмпирические математические  модели

• 2.    Из анализа расчетных данных и графиков (рисунки 2-4) выявлено следующее:

остаточной влажности кожи при валковом отжиме.

• •    с увеличением интенсивности нагрузки остаточная влажность кожи уменьшается;

• •    при прочих равных условиях функцию остаточной влажности от радиуса валка W ( R ) можно считать линейно-возрастающей;

• •    при прочих постоянных параметрах с увеличением скорости валка остаточная влажность увеличивается и асимптотически приближается к определенной величине (например, при 2 = 15 кН / м, R = 0,058 м значение

  

  влажности кожевенного полуфабриката

  
  

влажности кожевенного полуфабриката от интенсивности нагрузки Q,kH/м, когда V = 0,20м /c .

Figure 2. Residual moisture content of leather semi-finished product from intensity load Q,kH/ м when V = 0,20 м /c .

от скорости валка V, м / c , когда R = 0,10 м .

Figure 3. Dependence of the residual moisture content of the semi-finished product on the roll speed V, м / c when R = 0,10 м .

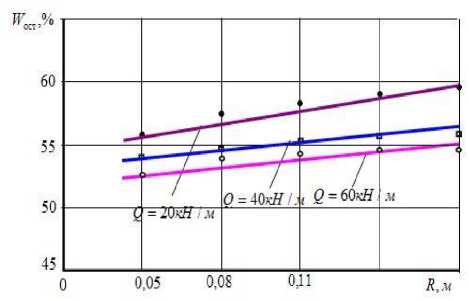
Рисунок 4. Зависимость остаточной влажности кожевенного полуфабриката от радиуса валка R, м, когда V = 0,10 м / с.

Figure 4. Dependence of the residual moisture content of the leather semi-finished product from the roll radius R, м, when V = 0,10 м / с .