Экспериментальное исследование процессов холодного фальцевания текстильных материалов

Процессы фальцевания текстильных материалов достаточно широко используются в швейном и галантерейном производстве: при формовании накладных карманов и воротников сорочек, формовании прорезей под «молнию» в кожгалантерейном производстве и др. Несмотря на это, в литературе [1,2] практически отсутствуют какие-либо сведения о результатах исследований режимов фальцевания.

В настоящей работе изложены результаты экспериментального исследования холодного фальцевания текстильных материалов. На процесс фальцевания текстильных материалов из синтетических волокон влияют следующие факторы: 1) сырьевой состав материала (X 1 ); 2) толщина материала (X 2 ); 3) удельное усилие прессования (X 3 ); 4) время фальцевания (X 4 ); 5) площадь фальцующего воздействия (X 5 ); 6) влажность материала (X 6 ); 7) температура фальцующих поверхностей (X 7 ). В проведенном эксперименте рассматривался процесс холодного фальцевания, то есть неучтенными оставались факторы X 6 , X 7 .

Сначала был проведен предварительный трехфакторный эксперимент (X 3 , X 4 , X 5 ) для X 1 =const (ацетатно-вискозный подкладочный материал арт.35112 ГОСТ 4.51-87) и для X 2 =const=1мм. Экспериментальные образцы: куски материала 50×10 мм.

Измеряемая величина (критерий оптимизации) – угол смятия α° между фальцуемыми краями (ГОСТ 10681-75, ГОСТ 19204-73). Помимо правильного угла смятия (рисунок 1а) на практике возникают следующие варианты: разновеликий угол смятия для разных краев участка (рисунок 1б), искривление свободного конца материала (рисунок 1в). Предварительный объем выборки n=20. Удельное

S технологическое давление в эксперименте определяется по формуле q = p ^п , S т где p – давление масла в гидроцилиндре пресса, Н/см² (см. рис. 2); S п – площадь рабочей поверхности поршня пресса, см²; S т – площадь технологической поверхности, см².

Экспериментальное оборудование: экспериментальный пресс гидравлический УП4 с максимальным усилием на штоке 40 кН, бруски металлические, формующие пластины, секундомер. Схема установки представлена на рисунке 2, где позициями обозначены: 1 – неподвижная опора, 2 – подвижная опора, 3, 4 – металлические бруски, 5 – формующие пластины, 6 – пластины с экспериментальным образцом. Измерительное оборудование: транспортир учебный с пределом измерения 1°. Матрица факторов представлена в таблице 1.

Рисунок 1 – Варианты исполнения угла смятия

Таблица 1 – Матрица факторов

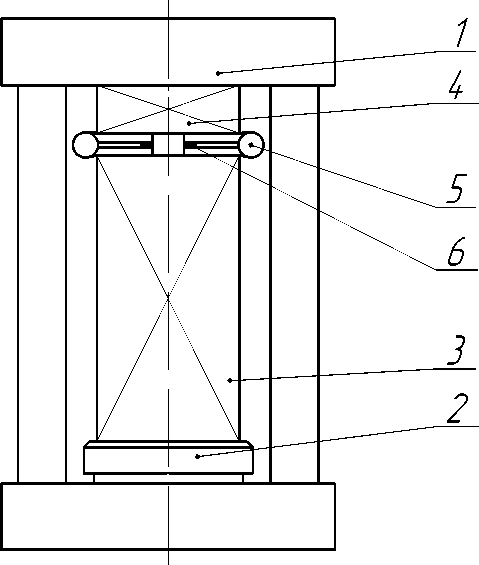
Рисунок 2 – Схема экспериментальной установки

Проведя эксперимент для приведенных в таблице 1 уровней варьирования факторов, обнаружили грубое нарушение закона нормального распределения для измеряемой величины. Это вызвано наличием большого числа неучтенных факторов: 1) различными механическими свойствами участков материала из-за переплетения продольных нитей основы поперечными нитями утка; 2) ошибок эксперимента: неравномерности распределения давления по площади образца, обусловленной непараллельностью поверхностей, передающих давление образцу, непостоянства давления во времени из-за утечек масла в клапанах пресса; 3) ошибок регистрации факторов (времени и давления) и измерения критерия оптимизации. Увеличение выборки не позволяло добиться нормального распределения для измеряемой величины. Попытка ввести новый фактор – расположение линии сгиба относительно направления нитки основы – позволил лишь отчасти приблизить распределение измеряемой величины к нормальному закону, но достичь его не удалось. При этом необходимо учитывать, что данный фактор трудно изменять при технологии фальцевания. Усложнить оборудование для снижения экспериментальных погрешностей не представлялось возможным. В результате принято решение отказаться от заданного критерия оптимизации (угла α) с относительной шкалой, а воспользоваться критерием оптимизации, имеющим номинальную (категориальную) шкалу измерения [3]. В качестве такого критерия удобно использовать частоту М В получения положительного результата процесса фальцевания (частоту появления события α=0°). Случайная величина М В может принимать одно из n+1 возможных значений m, равных 0, 1, 2, . . ., n. Выборочная численность М В является дискретной случайной величиной, математически определяемой биномиальным законом распределения. Статистические характеристики для такого рода случайной величины определяются следующим образом: математическое ожидание jtf(Me) = , дисперсия S(M_e) = i , среднеквадратическое отклонение c^Mg) = J л, где p - вероятность того, что результат эксперимента положительный (α=0°), q - вероятность обратного события, т.е. 9 = 1-. Для некоторых комбинаций факторов при n=20 получим результаты, сведенные в таблицу 2.

Таблица 2 – Результаты предварительного эксперимента

Вероятность выпадения того или иного значения m для случайной величины рассчитывается по формуле Бернулли iLM = i№™. Расчет коэффициентов – членов бинома Ньютона является трудоемким для больших значений n. Однако в силу того, что случайная величина М В является суммой одинаково распределенных вспомогательных случайных величин X 1 , X 2 , . . . , X n (каждая их которых может принимать одно из двух значений – 0, 1) с определенными математическими ожиданиями и дисперсиями, к изучаемой случайной величине можно применить теорему Ляпунова и следствие из нее. А значит при высоких значениях n ( n > J) случайная величина М В следует приближенно нормальному закону распределения. Поэтому требуется повысить выборку до 100 измерений в каждом опыте. Учитывая улучшение качества фальцевания при контактной площади фальцующего воздействия, принимаем фактор X 5 =const (контактная площадь). Для данных условий получили следующие значения вероятности, сведенные в таблицу 3.

Таблица 3 – Результаты эксперимента

Как видим, необходимая нам вероятность достигается при достаточно высоком значении времени. Эксперимент уточняем и проводим его для уровней варьирования факторов, сведенных в таблицу 4, а результаты сведем в таблицу 5.

Таблица 4 – Матрица факторов

Таблица 5 – Результаты эксперимента

Коэффициенты регрессии для полинома, описывающего линейную регрессию, будут следующими: b 0 =0,9175, b 3 =0,0225, b 4 =0,0675, b 3,4 =-0,0075 [3]. Таким образом, поверхность отклика, ограниченная данными пределами уровней варьирования, аналитически описана уравнением:

p = 0,9175 + 0,0225 X 3 + 0,0675 X 4 - 0,0075 X 3 X 4 .

После проведенного эксперимента по изучению процесса холодного фальцевания установили значимые факторы, определили коэффициенты регрессии для значимых факторов. Коэффициент регрессии для фактора времени (X 4 ) оказался выше в 3 раза коэффициента регрессии для фактора технологического давления (X 3 ), что снижает производительность процесса холодного фальцевания. Учитывая это, при выборе режимов процесса фальцевания следует помнить о невысокой производительности процесса холодного фальцевания, что допускает его использование: а) для материалов с высоким коэффициентом сминаемости, б) в случае параллельного сочетания процесса с другими формирующими ориентированное смятие операциями (стачивание, склеивание и др.).