Экспериментальное исследование влияния сыпучего материала на устойчивость при изгибе тонкостенных оболочек с сыпучим заполнителем

ВЕСТНИК ПНИПУ. МЕХАНИКА № 4, 2019PNRPU MECHANICS BULLETIN

Оболочечные элементы строительных, авиационных конструкций, транспортных систем, автоцистерн, трубопроводов теряют устойчивость при изгибе. Потеря устойчивости пустых тонкостенных цилиндрических оболочек при изгибе рассматривалась во многих трудах отечественных и зарубежных ученых [1–17].

Рассмотрена устойчивость оболочек гладких и подкрепленных, изотропных и анизотропных, деформируемых в пределах и за пределами упругости различной формы. Мало исследована потеря устойчивости и за-критическое упругопластическое деформирование тонкостенных оболочек при их взаимодействии с сыпучим наполнителем [18–24]. Проблема устойчивости при изгибе автоцистерн для перевозки сыпучих материалов появилась в связи с началом их производства на предприятии ЗАО «Чебоксарское предприятие „Сеспель“». На рис. 1 показана подъемная автоцистерна, которая при подъеме с одного конца для выгрузки сыпучего наполнителя изгибается, деформируется, может потерять устойчивость.

Цистерна представляет собой тонкостенную оболочку. Задача устойчивости при изгибе оболочки с сыпучим наполнителем является трехмерной, геометриче- ски и физически нелинейной с учетом возможных необратимых деформаций конструкции [18]. Численный анализ деформирования, потери устойчивости и закри-тического поведения большегабаритных емкостей для автомобильной транспортировки сыпучих грузов производился в исследованиях [18–23].

Рис. 1. Подъемная автоцистерна

Fig. 1. Lifting tanker truck

Определяющая система уравнений сформулирована в переменных Лагранжа в трехмерной динамической постановке [18]. Упругопластическое деформирование описано соотношениями теории течения [22–23]. Геометрическая нелинейность учтена с помощью пересчета геометрии оболочки в каждый момент времени. Численное решение задачи основано на методе конечных элементов и явной конечно-разностной схеме интегрирования по времени типа «крест» [18]. Численные исследования выполнялись в рамках вычислительного комплекса «Динамика-3», аттестованного в научно-техническом центре по ядерной и радиационной безопасности [25] и Госстандарте РФ [26].

Экспериментальные исследования выполнялись на модельных образцах из разных материалов [19–21]. Образцы закреплялись консольно или на двух шарнирных опорах [20]. Размеры образцов рассчитаны так, чтобы результаты экспериментов можно было перенести, используя коэффициенты подобия, на натурные цистерны. Исследовалось поведение пустых и заполненных сыпучим материалом образцов, определялась критическая нагрузка, изучалось влияние геометрических размеров, геометрических несовершенств образцов на предельную нагрузку [20–23]. Выполнена верификация численной методики расчета экспериментами. Численные расчеты и эксперименты показали, что для оболочек, заполненных сыпучим материалом, предельные нагрузки возрастают. Влияние сыпучего наполнителя на устойчивость изучена недостаточно. Поэтому исследование влияния сыпучего наполнителя на устойчивость оболочек является актуальным и необходимым для производства автоцистерн.

Цель работы – изучить влияние сыпучего заполнителя на устойчивость при изгибе тонкостенных цилиндрических оболочек применительно к автоцистернам, изготавливаемым на предприятиях.

1.    Экспериментальная установка, образцы, материалы

Экспериментальная установка показана на рис. 2, где 1 – жесткая металлическая стенка; 2 – индикатор часового типа ИЧ-10; 3 – штатив; 4 – образец; 5 – нагружающее устройство.

Рис. 2. Экспериментальная установка

Fig. 2. Photo of the facilities

Для измерения деформаций на предполагаемое место потери устойчивости наклеивались тензодатчики марки КФБП1-10-200 в продольном направлении. Деформации фиксировались измерителем деформации «Терем-4». Материал образцов – алюминиевый сплав 3004 в состоянии Н19. Сыпучим материалом был железный порошок ПЖ-5. Образцы изготавливались глубокой вытяжкой, тщательно отбирались, чтобы не было дефектов. Размеры образцов приведены в табл. 1.

Таблица 1

Размер образцов

Sample size

Table 1

Серия испытаний	Радиус R , мм	Толщина стенки h , мм	Длина L , мм	h / R	L / R
1	32,8	0,1	135	0,003	4,12
2	32,8	0,1	270	0,003	8,24
3	41,65	0,12	165	0,0029	3,96

2.    Проведение экспериментов

Эксперименты выполнялись на консольно закрепленных образцах, на свободный конец которых прикладывалась поперечная сила F . Прогиб свободного конца образца «y» измерялся индикатором часового типа ИЧ-10. Для каждой серии экспериментов испытывалось по десять образцов. Выполнялось ступенчатое нагружение порциями по 10 Н, при приближении к моменту потери устойчивости нагружали по 1Н и менее, на каждой ступени нагружения фиксировали усилие, прогиб свободного конца, деформацию в продольном направлении.

3.    Результаты экспериментов и численных расчетов

Выполнялась статистическая обработка результатов экспериментов. По результатам экспериментов построены графики y = f ( F ), изображенные на рис. 3.

Результаты экспериментов и численных расчетов критических сил приведены в табл. 2. Доверительный интервал для значений критических сил F _cr, измеренных в экспериментах для пустых образцов третьей серии, равен (0,254;0,27)кН, а для таких же образцов, заполненных железным порошком на 90 % объема, равен (0,333;0,349)кН. Численные расчеты выполнены с помощью вычислительного комплекса «Динамика-3».

Для пустых и заполненных образцов графики на рис. 3 почти совпадают до потери устойчивости пустых образцов и изменяются линейно. Устойчивость образцов теряется при сжимающих напряжениях, меньших предела текучести материала. Вмятины образуются в зоне наибольших сжимающих напряжений перемещением элемента образца внутрь, к оси образца, однако перемещениям противодействует давление сыпучего материала, начинается влияние сыпучего материала на устойчивость, поэтому критическая поперечная нагрузка возрастает, возрастает критическое осевое напряжение σ _cr .

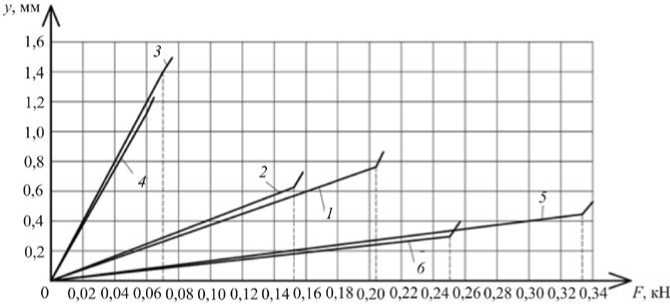
Рис. 3. Зависимость прогиба свободного торца образцов от поперечной силы: 1 , 3 , 5 – для образцов с сыпучим материалом для первой, второй, третьей серии; 2 , 4 , 6 – для пустых образцов для первой, второй, третьей серии соответственно

Fig. 3. Dependence of a deflection of the free end face of samples on cross force: 1, 3, 5 are for samples with a loose material for the first, second, third series; 2, 4, 6 are for empty exemplars for the first, second, third series respectively

Таблица 2

Результаты экспериментов и численных расчетов критических сил

Table 2

Results of experiments and numerical calculations of critical forces

Серия испытаний	Процент заполнения образца, %	Критическая сила F cr , кН		Расхождение F cr , %	Процент увеличения Fcr для заполненного образца (эксперимент)
		Эксперимент	Численный расчет
1	0 (пустой)	0,153	0,16	4,5	41
	90	0,215	0,223	3,7
2	0	0,060	0,063	5	17
	90	0,070	0,0747	6,7
3	0	0,262	0,269	2,7	30
	90	0,341	0,349	2,3

Измеренные тензодатчиками в зоне потери устойчивости продольные деформации позволили подсчитать осевое критическое напряжение σ _cr . Например, для пустых образцов первой серии σ cr = 45…60 МПа, а предел текучести материала σ _y = 324 МПа. Критическое напряжение значительно меньше предела текучести. Критическое напряжение σ _cr для заполненного на 90 % объема образца, равно 85,4 МПа, это в 1,4 раза больше, чем σ cr для пустого образца. Для заполненных образцов первой серии критическая сила увеличилась на 41 %, для второй серии – на 17 %, для третьей серии – на 30 %. Критические силы, измеренные экспериментами и рассчитанные численными расчетами, отличаются максимально на 6,7 %.

4.    Приближенный расчет σcr

На предприятиях нет вычислительного комплекса «Динамика-3», поэтому разработан приближенный метод расчета на устойчивость [24].

В приближенных расчетах критическое напряжение σcr рассчитывается по формуле

\              h M pgHR acr=acr +^+^2= k (l) Е — + — +     , cr cr  12     RW 2h

где Е – модуль упругости материала оболочки; h – толщина стенки; R – радиус образца. Коэффициент k ( l ) принимает значения 0,3 для оболочек средней длины, 0,22 – для более длинных оболочек; М – изгибающий момент от весовой нагрузки в месте потери устойчивости; W – осевой момент сопротивления поперечного сечения; ρ – плотность заполнителя; H – высота уровня заполнения; g = 9,8 м/с².

Первое слагаемое в формуле (1) определяет критическое напряжение для пустой оболочки [1]. Второе и третье слагаемые определяют влияние заполнителя на критическое напряжение. Второе слагаемое в формуле (1) определяет осевое напряжение от изгибающего момента весовой нагрузки. Третье слагаемое определяет осевое напряжение, создаваемое давлением сыпучей среды в зоне образования вмятин, которая получена преобразованием формулы для расчета осевого напряжения, возникающего в тонкостенных цилиндрических оболочках, находящихся под действием внутреннего давления [24].

Рассмотрим влияние сыпучего наполнителя ПЖ-5 на устойчивость для образцов первой серии:

ст = 0,3Е h = 0,3.0,7.105. 0,1 / 32,8 = 64 МПа. cr         R где Е – модуль упругости материала образцов, Е = 0,7·105 МПа.

Равномерно распределенная весовая нагрузка

m q = 7

12,9 - 10 ^{- 6}

135 - 10 - ³

= 0,0956 - 10 - ³

MH

, м

где m – масса загрузки, m = 12,9·10^–6 МН.

Осевой момент сопротивления

W — n hR ² = 3,14 ■ 0,1 - 32,8 2 - IO ^{- 9} = 0,34 ■Ю^{- 6} м³,

ql ²

°, =----

1   2 W

0,0956 - 10 ^{- 3} ■ 135 2 ■Ю^{- 6}

2 ■ 0,34 - 10 ^{- 6}

= 2,56 МПа.

_ p gHR

°

2      2 h

2,62 - 10 ^{- 2} - 10 ■ 64 - 10 ^{- 3} ■ 32,8 - 10 ^{- 3}

2 ■ 0,L10 ^{- 3}

— 2,75 МПа,

где ρ – насыпная плотность железного порошка, ρ = = 2,62·10^–2 МН/м³; Н – высота загрузки, Н = 64·10^–3 м.

° cr — ° Cr + ° 1 + ° ₂, — 64 + 2,56 + 2,75 — 69,3 МПа.

Расхождение между опытным значением σ _cr = 85,4МПа и рассчитанным по приближенной формуле (1) значением σ _cr = 69,3 МПа составляет 18,8 %. Численными расчетами в программе «Динамика-3» получено о cr , равное 86 МПа. Влияние ° 1 и ° ₂ на устойчивость малое, составляет 8,3 %.

Рассмотрим влияние сыпучего материала на устойчивость для натурных цистерн. Пусть цистерна имеет следующие размеры: R = 1,27 м; h = 8·10^–3 м; l = 6 м; Е = 0,7 ·10⁵ МПа. Материал цистерны – алюминиевый сплав марки АМг5. Загружена цистерна железным порошком на 90 % объема насыпной плотностью ρ = 2,62·10^–2 МН/м³. Цистерна опирается на две концевые шарнирные опоры.

Объем цистерны V = π R ²l = 3,14·1,27²·6 =30 м³.

Объем загрузки V ₁ = 0,9 V = 0,9·30 = 27,3м³.

Масса порошка m = ρ V 1 = 2,62·10^–2·27,3 = 0,71МН.

Равномерно распределенная весовая нагрузка m 0,71MH q — — —----— 0,12.

l6м

Осевой момент сопротивления

W = π hR ² = 3,14·8·10^–3·1,27²= 0,04 м³.

о' — 0,22 Е - — 0,22 ■ 0,7 ■1058■10- — 97 МПа, cr          R1,27

На предприятиях изготавливают автоцистерны размером R = 1,25 м; h = 10·10^–3 м; l = 16 м.

5. Влияние различных сыпучих материалов и процента загрузки объема оболочки на предельное состояние

Экспериментально изучено на образцах первой серии. Образцы загружались речным песком р — 1,52г/см³, железным порошком р — 2,62г/см³, медным порошком р — 3,54г/см³. Значения критических нагрузок и критических напряжений для образцов, заполненных различными сыпучими материалами на 90 % объема, представлены в табл. 3.

Таблица 3

Значения критических нагрузок и критических напряжений

Table 3

Values of critical loads and critical stresses

Тип порошка	Плотность ρ, г/см3	Критическая нагрузка F cr , кН	Критическое напряжение опытное σ cr ,МПа	По формуле (1) σ cr , МПа	Рсхож-дение σ cr , %
Железный	2,62	0,215	85,4	69,3	18,8
Медный	3,54	0,217	78	70,38	9,7
Речной песок	1,52	0,163	64,7	66,9	3,4

° 1

ql ²

8 W

0,12 ■ 36

8 ■ 0,04

— 13,5 МПа.

Из табл. 3 видно, что критическое напряжение для образцов 1-й серии, загруженных железным порошком на 90 % объема, отличается от критического напряжения, рассчитанного по формуле (1), максимально на 18,8 %. Следовательно, для расчета критического напряжения можно пользоваться формулой (1).

Увеличение критических нагрузок на образцы, заполненные различными сыпучими материалами на различные объемы, относительно критических нагрузок на пустые образцы, представлено в табл. 4.

Таблица 4

Увеличение критических нагрузок

° — ^p gHR — 2,62 ■ 10 ^{- 2} ■ 9.8 ■ 2,3 ^1,27 — 46,8 МПа,

²     2 h                            2 ■ 8 ■Ю ^{- 3}

где Н = 2,3 м.

Критическое напряжение

° cr — ° Сr +° 1 + ° 2 , — 97 + 13,5 + 46,8 — 157,3 МПа.

Критическое напряжение за счет действия сыпучего заполнителя возрастает на 62 %.

Ясно, что для натурных цистерн влияние сыпучего материала на устойчивость при изгибе значительно.

Table 4

The increase in critical loads

Вид сыпучего материала	Объем заполнения
	на 30 %	на 60 %	на 90 %
Речной песок	2	3,27	13
Железный порошок ПЖ-5	4	7,84	41
Медный порошок	7,84	17,65	43

Зависимости критической силы от процента наполнения образцов показаны на рис. 4.

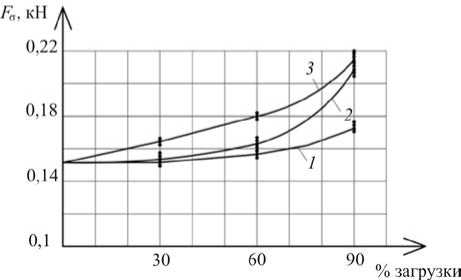
Рис. 4. Графики зависимости критической силы от процента загрузки: 1 – для речного песка; 2 – для железного порошка ПЖ-5; 3 – для медного порошка

Fig. 4. Dependence of the critical force on the loading per cent:

• 1    – for river sand; 2 – for iron powder PZh-5;

• 3 – for copper powder

Из анализа результатов табл. 4 и рис. 4 можно сделать вывод, что с увеличением плотности сыпучего наполнителя и процента заполнения объема оболочки критическая сила возрастает.

Образец первой серии, заполненный железным порошком на 90 % объема, после потери устойчивости при критической нагрузке F cr = 0,214кН, показан на рис. 5, а , форма того же деформированного образца, полученная в результате численного моделирования, показана на рис. 5, б . Характер деформаций образцов после потери устойчивости во всех случаях одинаковый.

а

б

Рис. 5. Деформированный образец: а – образец первой серии, заполненный на 90 % объема; б – образец, полученный численным моделированием

Fig. 5. The deformed sample: a – first series filled to 90 % of the volume; b – obtained by numerical simulation

6.    Анализ результатов

Экспериментальные и численные исследования показали, что заполнение тонкостенных цилиндрических цистерн сыпучими материалами для их перевозки позволяет увеличить их устойчивость при изгибе. Важность и полезность работы подтверждается тем, что она финансировалась РФФИ (проект № 16-38-60051мол_а_дк). Критические силы, измеренные в экспериментах и рас- считанные численными расчетами, максимально отличаются на 6,7% (см. табл. 2), следовательно, эксперименты выполнены качественно, а численная методика вычислительного комплекса «Динамика-3» хорошо описывает процесс деформирования, потери устойчивости и закритического поведения пустых и заполненных сыпучим материалом тонкостенных оболочек. Влияние сыпучего наполнителя на устойчивость заключается в противодействии образованию вмятин. Для заполненных железным порошком образцов первой серии критическая сила увеличилась на 41 % по сравнению с критической силой для пустых образцов. Для расчета критического напряжения на предприятиях рекомендован приближенный метод расчета, который верифицирован экспериментами и численными расчетами. Расчет критического напряжения для автоцистерны показал, что железный порошок, заполнивший на 90 % объем цистерны, увеличивает критическое напряжение на 62 %. Устойчивость оболочек зависит от плотности наполнителя и процента заполнения объема. У образцов первой серии, заполненных речным песком насыпной плотностью ρ = 1,52 г/см3, при наполнении на 30 % критическая сила увеличилась на 2 %, при наполнении на 60 % критическая сила увеличилась на 3,27 %, при наполнении на 90 % – на 13 % (см. табл. 4). У образца, заполненного медным порошком ρ = 3,54 г/см3, при наполнении на 30 % критическая сила увеличилась на 7,84 %, при наполнении на 90 % критическая сила увеличилась на 43 %. С увеличением плотности сыпучего наполнителя и объема заполнения критическая нагрузка возрастает.

Заключение

• 1.    Сыпучий заполнитель влияет на критическую нагрузку оболочки при изгибе. С увеличением плотности и процента загрузки сыпучего материала критическая сила возрастает.

• 2.    При проектировании и изготовлении автоцистерн для перевозки сыпучего материала необходимо учитывать влияние заполнителя на устойчивость, в этом случае снижаются потребность в металле и стоимость.

• 3.    Формулой (1) можно пользоваться для расчета критических нагрузок на предприятиях, изготавливающих автоцистерны.

Работа выполнена при финансовой поддержке РФФИ (проект № 16-38-60051 мол_а_дк).

Acknowledgment

Work is performed with the financial support of the Russian Federal Property Fund (Project No. 16-38-60051 mol_а_dk)