Экспериментальное исследование возможностей решения многоэкстремальных задач оптимизации эвристическими методами

Введение. Многие современные проблемы науки, техники, экономики, военного дела и пр. связаны с решением задач поиска оптимальных характеристик объектов проектирования: конструкций, технологий, режимов и условий работы, динамических и статических состояний и т. д. Иными словами, разработчикам приходится решать задачи поисковой оптимизации (ПО) [1–3]. Характерно, что большинство известных на сегодня методов ПО разработано и эффективно используется для нахождения одного оптимума — чаще всего, глобального [3, 4]. Однако многие задачи планирования, сложные технологические комплексы, транспортные задачи и другие объекты оптимизации (особенно дискретной природы) характеризуются многоэкстремальностью (МЭ) [4–11]. Столь существенное отличительное свойство требует специфических методов решения таких задач. Вряд ли эти методы целесообразно искать в классе детерминированных методов ПО. Они слишком чувствительны к знакопеременности и разрывности функций отклика в конти- нуальных факторных пространствах, а также описываются NP-полными алгоритмами в дискретных факторных пространствах. Для решения большинства реальных оптимизационных задач все чаще стремятся применять методы, получившие название «эвристические». Эти методы наиболее перспективны и для решения МЭ задач [5–11].

Постановка задачи. В связи со сказанным во введении представляется актуальным и перспективным исследование наиболее распространенных эвристических методов ПО в среде какой-либо характерной МЭ задачи. Цель работы: установить возможность нахождения нескольких или всех экстремумов рассматриваемой области каждым из выбранных методов. Кроме того, необходимо оценить точность определения значений экстремумов и их координат. Поэтому первым этапом исследований является выбор тестовой МЭ функции, которая может послужить общей для всех методов средой решения МЭ задач.

Выбор многоэкстремальной тестовой функции и предварительный анализ ее свойств. Самыми распространенными и эффективными тестовыми функциями, используемыми для отладки и исследования методов ПО, являются функции Розенброка, Химмельблау и Растригина. Из них наиболее многоэкстремальная — функция Растригина (ФР). Эта невыпуклая универсальная функция предложена в 1974 году Леонардом Растригиным [12]. Уравнение функции N аргументов имеет вид:

f ( x ) = A × n + ∑ [ x_i 2 - A × cos(2 × π × x_i )]                                           (1)

i = 1

где A = 10.

Глобальный минимум этой функции — f mglin ( 0 ) = 0 .

Нахождение глобального минимума данной функции представляет собой достаточно трудную задачу из-за большой области поиска и количества локальных минимумов, на которых алгоритм может зацикливаться. Выделение и оценка локальных экстремумов является еще более сложной и неординарной задачей.

Исследование ФР алгоритмом роящихся частиц . Сущность и основания для использования в задачах ПО метода роящихся частиц (МРЧ) хорошо известны [13–17]. Классический алгоритм МРЧ имитирует реальную групповую поведенческую модель насекомых, птиц, рыб, многих простейших и т. п. Однако МЭ объекта оптимизации требует некоторых специфических свойств алгоритма. Поэтому канонический вариант МРЧ был значительно переработан авторами [18–20] и другими учениками Р. А. Нейдорфа [7–11]. В частности, разработана его модификация для решения МЭ задач.

Модель механического движения (ММД) частиц [20] в МЭ МРЧ была существенно доработана и уточнена:

X* = X(t-a t)i + V (t-w*a t,(2)

• —           ——

Vti = V(t-Δt)i+A(t-Δt)i×Δt ,(3)

—          ——

Ai = Api+ Atri ,(4)

где X (t _-a t)i — предыдущее положение i-й частицы; X i — ее текущее положение; V _ti — скорость i-й частицы в текущий момент времени; / (_{t -А t})i — предыдущая скорость частицы; Й^ _{-a t)i} — предыдущее ускорение частицы в предыдущий момент времени; Δ t — интервал интегрирования по времени; A pi — ускорение под действием биологически обусловленных сил притяжения частиц; A tri — замедление под действием сил трения.

Для улучшения поисковых свойств было введено стохастическое размытие параметров:

λ^ξ ( ε ) =λ× ( 1 + 2 ×ε (rnd( 1 ) - 0 , 5 )) ,                                         (5)

где λ^ξ ( ε ) — значение флуктуирующего параметра на такте вычисления; ε — относительное отклонение искажаемого параметра от номинального значения; rnd( 1 ) — случайное число в диапазоне [0, 1].

Предложены и проверены механизмы естественной кластеризации частиц, порождаемой и параметрически настраиваемой свойствами алгоритма:

— градиентный, основанный на чувствительности частиц к смене знака скорости изменения оптимизируемого критерия исследуемого объекта [7–9];

— потенциальный, основанный на введении в ММД сил притяжения ко всем обнаруженным при роении и сканировании пространства поиска локальным экстремумам:

• ——      —— _G    ^— _L ^— _C

A pi ⁼ A pi ⁺ A pi ⁺ A pi .                                                (6)

Информатика, вычислительная техника и управление

Здесь A pGi — притяжение частицы к глобальному экстремуму; A pLi — притяжение частицы к локальному экстремуму; A Cpi — притяжение частицы к центру ближайшего кластера.

Алгоритм МЭ МРЧ показал хорошую избирательность при локализации областей экстремумов, однако механизмы кластеризации и локализации кластеров потребовали существенной структурной и параметрической доработки. В настоящем исследовании введены и проверены следующие модификации:

• —    механизм отсева по определенным критериям «плохих» кластеров (являющихся худшими на заданном числе итераций);

• —    механизм объединения схожих кластеров на каждом шагу;

• —    настройка условного притяжения к центру ближайшего кластера;

• —    механизм локализации областей кластеров и поиска в них параметров локальных экстремумов.

Эффективность модификаций проверена ФР в диапазоне координат ( x , y ) _∈ [ _- 1.5,1.5] . В этой области ФР имеет 9 локальных минимумов, один из которых является глобальным.

На рис. 1 отображен процесс локализации областей экстремумов и создания соответствующих кластеров.

а)                                         б)

Рис. 1. Локализация областей экстремумов: 1-я итерация (а); 50-я итерация (б)

Как видно из рис. 1, частицы изначально притягивались к образовавшемуся кластеру, который располагался в области глобального экстремума. Затем периферийные частицы находили локальные экстремумы, притягивались к ним и собрались в кластеры. В суженных областях кластеров применение алгоритма МЭ МРЧ (на случай наличия менее выделенных и значимых экстремумов) повторяется. Этот процесс итеративно повторяется до получения требуемой точности оценки параметров всех локальных и глобального экстремумов.

На рис. 2 отображены фрагменты итеративной идентификации локального экстремума, который располагается в точке [–1, 1].

а)

б)

в)

Рис. 2. Локальная идентификация одного из локальных экстремумов: 15-я итерация (а); 33-я итерация (б); 50-я итерация (в)

В табл. 1 отображены результаты, полученные локализацией всех областей, приведены координаты x = x 1 и y = x 2 , а также значения ФР, полученные по формуле (1). Как видно, получены удовлетворительные результаты с временными затратами ~149 с. С увеличением числа итераций (и времени поиска) точность оценки повышается.

Таблица 1

Результаты проведенного опыта

Эталон			Параметры оценки экстремума
x	y	f (x, y)	Координаты		Значение
			x	y	f (x, y)
-1	1	2	-0,9957	0,9953	1,9901
-1	0	1	-0,9949	0,0001	0,995
-1	-1	2	-0,9951	-0,9947	1,9899
0	1	1	-3,20x10 - 5	0,9948	0,995
0	0	0	9,85x10 - 5	-6,49x10 - 6	1,94x10 - 6
0	-1	1	0,00017	-0,995	0,995
1	1	2	0,9949	0,995	1,9899
1	0	1	0,995	0,00011	0,995
1	-1	2	0,9952	-0,9951	1,9899

Для решения задачи МЭ МРЧ использован ПК c процессором AMD Phenom II P960, оперативная память — 6Gb. При этом для достижения точности 1E-3 удалось ограничиться 50 итерациями и осуществить локализацию областей экстремумов с затратами по времени — 149 с. При дополнительном исследовании каждой из областей потребовалось в среднем — 2,5-3,5 мин на одну область и порядка 30 мин на все 9 областей.

Таким образом, можно сделать вывод, что МЭ МРЧ является эффективным инструментом решения МЭ задач. Исследование ФР эволюционно-генетическим алгоритмом. Эволюционно-генетический алгоритм (ЭГА) является одним из наиболее востребованных инструментов решения оптимизационных задач [21-24]. Структура и основные операторы ЭГА хорошо известны, а конкретные структурно-параметрические особенности зависят от предметного приложения. В частности, применение ЭГА для решения МЭ задач [25-28] требует дополнения классического ЭГА инструментами селектирования экстремумов — по типу (максимум, минимум), по величине, а также по координатам его положения в факторном пространстве. В данной работе развивается подход к селекции экстремумов, основанный на использовании одновыборочного критерия Стьюдента [27-29]. Сущность данного подхода может быть представлена следующим образом. При последовательном использовании ЭГА результаты, полученные в финишных поколениях, кластеризуются, т. е. разделяются по координатным группам. С этой целью для каждого результата проверяется 0-гипотеза.

Математическая модель данного подхода кластеризации заключается в последовательном сравнении векторов со средним значением группы векторов v = {Avi = vi-vо|i = У,n} , где n — количество векторов группы.

Относительно заданной доверительной вероятности принимается решение о принадлежности вектора v существующему множеству. Для уточнения принадлежности необходимо рассчитать среднее значение длин векторов группы, с которой производится сравнение:

Av = Zn=i Av/n .(7)

После необходимо вычислить стандарт отклонения длин векторов уже обозначившегося кластера:

S{av} = n(Av-v)2/(n -1) ,(8)

i = 1

S{Av} = S{Av}/^ .(9)

По вычисленным величинам рассчитываются опытные значения одновыборочного критерия Стьюдента:

Информатика, вычислительная техника и управление

t 0 = | A v -A v|/S { д v} . (10)

Если найденное опытное значение t₀ не превосходит табличного [30] значения t r при n степеней свободы и выбранном в таблице уровне доверительной вероятности P , то можно считать, что t₀ принадлежит данной группе объектов.

Данный метод хорошо зарекомендовал себя при исследовании МЭ зависимостей [27-31].

С учетом этого подхода разработаны алгоритм и программное средство (ПС) на его основе. С помощью ПС ФР рассмотрена в том же диапазоне, что и в предыдущем разделе статьи при исследовании ФР алгоритмом роящихся частиц.

Структура входных параметров ЭГА, которая была использована при исследовании ФР, включает в себя поколений — 10, особей в каждом поколении — 1000, вероятность кроссинговера — 95 % и мутации — 30 %. Стоит отметить, что параметр области поиска используется тот же, что и в предыдущем разделе, а точность исследования в этой области равна 7 разрядам после запятой. В результате выделено 9 кластеров, минимумы которых можно соотнести с теми минимумами ФР, которые попали в исследуемую область.

На рис. 3 отображены графики последовательного нахождения значений ФР и их различных координат (X и Y), а также соответствующие им значения целевой функции (F (X, Y) = 2), которые, в свою очередь, упорядочены по убыванию (для кластеров, образованных вокруг минимумов со значениям (-1;1), (1;-1), (1;1), (-1;-1)).

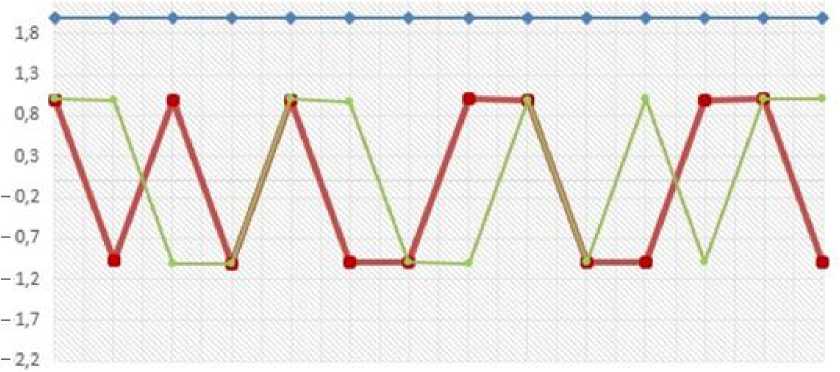
--F(X,Y) • X--Y

Рис. 3. Выделение кластеров в ходе эксперимента

На рис. 4, а восемь периферийных кластеров характеризуют локальные минимумы, а центральный кластер содержит результаты, приближающиеся к глобальному минимуму функции. Хорошо видно, что близкие (а в некоторых случаях равные) по значению функции цели имеют существенные отличия по координатным показателям (т. е. параметры функции цели, обеспечивающие близкие к минимуму значения, разнятся). Данный факт подтверждает много-экстремальность исследуемого объекта.

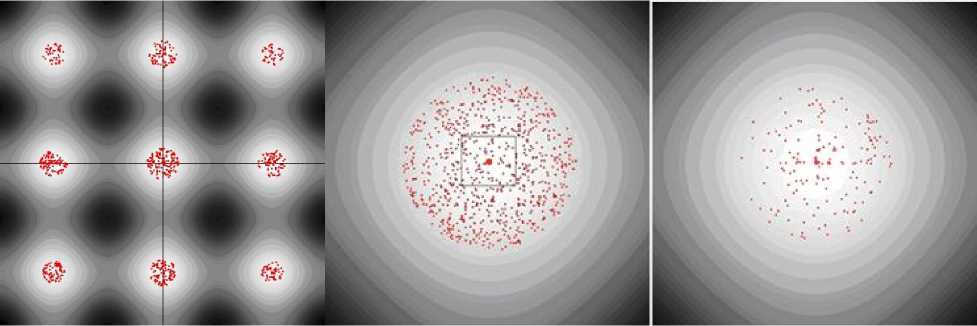
а)

б)

в)

Рис. 4. Локализация областей экстремумов. Выделенные кластеры ФР (а) и формирование кластеров в локализованной области: 100-е поколение (б); 110-е поколение (в)

Результаты исследования функции (как на глобальный, так и на локальные минимумы) отображены в табл. 2.

Таблица 2

Найденные параметры функции цели первой итерации (по кластерам)

Эталон				Параметры оценки экстремума
№	x	y	f ( x, y )	Координаты		Значение
				x	y	f ( x, y )
1	0	0	0	0,00188	0,00015	0,00071
2	-1	0	1	-0,98932	0,00073	1,00137
3	0	-1	1	0,00824	-1,00043	1,01436
4	1	0	1	0,99948	-0,01328	1,03398
5	0	1	1	0,01403	1,00665	1,0611
6	1	-1	2	0,99146	-0,99314	1,993
7	1	1	2	0,99702	1,00467	2,00947
8	-1	-1	2	-0,9897	-1,01397	2,06707
9	-1	1	2	-1,00528	1,00077	2,01775

Как видно из табл. 2, оценки значений экстремумов и их координат не отличаются высокой точностью. В случае, если найденные значения не удовлетворяют требуемой точности, реализуется повторное исследование минимумов функции в области кластеров.

В качестве примера приводятся исследования областей кластеров 2, 4 и 8 методом локализации поисковой области [29] (табл. 3). Дальнейший поиск значений осуществляется использующим ЭГА методом, разработанным авторами [27, 28].

Наглядно кластер найденных ЭГА статистически близких значений в одной из областей можно наблюдать на рис. 4, б. Наилучшая оценка экстремума выделена жирной точкой. Для повышения точности оценки вокруг этого субэкстремума программой выделяется область дополнительного исследования, результаты анализа которой визуализированы на рис. 4, в.

Уточненные на второй итерации значения функций цели, а также соответствующих им координат приведены в табл. 3.

Таблица 3

Найденные параметры значения функции цели второй итерации

	2-й кластер	4-й кластер	8-й кластер
Значение X	-0,999996	0,999992	-0,999996
Значение Y	0,000005	-0,000008	-1,000005
Значение ФР	0,999997	0,999989	1,999991

Исследование ФР муравьиным алгоритмом. Муравьиные алгоритмы (МА) — еще одна группа методов, которая используется в различных оптимизационных задачах. Их отличительная особенность заключается в имитации ключевых черт поведения настоящих муравьев [32]. Чаще всего МА применяются к задачам минимизации пути на графах [33], однако данные алгоритмы показывают хорошие результаты и в других областях [34, 35]. В представленной работе рассмотрено применение классического МА для МЭ оптимизации эталонной двухпараметрической ФР [12].

В основе описываемого метода лежит классическая реализация МА, применяемая к задачам на графе [36, 37, 38], но с некоторым дополнением. Рассматриваемое пространство делится на равные участки [39].

Как и в классическом МА, в данной модификации выделяются такие этапы, как «расстановка и инициализация», «осуществление перехода» и «проверка условия останова».

В качестве примера был рассмотрен фрагмент ФР для x е [ - 1.5,1.5], у _е [ - 1.5,1.5]- Он разделен на nxn участков, каждый из которых ассоциируется со значением функции в центре и наделяется некоторым количеством феромона. На участок помещается A муравьев. Так как все участки одинаковые, то размеры фрагмента можно вычислить по формуле:

m = (X_max - X_min)/ n .                                            (11)

Информатика, вычислительная техника и управление

Таким образом, множество участков представлено матрицей A = (Ii,j)i=q,j=1. Муравей в участке h,j оцени- вает все смежные с ним участки и рассчитывает вероятности перехода по формуле:

P ij , k ⁽ t ) = <

^v f ⁽ x i , j , y i , j ) >  f ⁽ x i + 1, j + 1 , y i + 1, j + 1 ) ^ Q *^{; v} f ⁽ x i , j , y i , j ) ^ f ⁽ x i + 1, j + 1 , yi + 1, j + 1 ) ^ °,

где Q * ( T i + 1 j + 1 , т i,j , n _{i + 1} ,j _{+ 1} , Пр , a , в ,t) — функция количества феромонов в ячейках — ^т i + 1, j + 1 ’ ^т i , j ; p i _{+ 1} ■₊₁ , p i • =

Vf(xt -,y- ) - f(x i +i +i ,У-    )l ¹ — вес (виртуальная дистанция) между двумя участками; a — изменяемый коэф ,          i , j                     ,                     i I 1 , j I 1

фициент воздействия феромона; в — изменяемый коэффициент весового воздействия; t — номер итерации.

Структура функции Q( т i _{+ 1} ,j _{+ 1} , т i,j , П i _{+ 1} ,j _{+ 1} , Пр , a , в ,t) может быть различной [39].

Модель (12) дополняется моделью обновления феромона (13). На каждой итерации происходит прирост и испарение феромона. Таким образом, приращение количества феромона за шаг моделирования в участке I i j рассчитывается по следующей формуле:

т у/ + ¹ ) = ^{( 1 —р} ) *T ij ^(t) + ^AT iJ ^(t)                                        .⁽¹³⁾

Здесь ре ( 0 , 1 ) — коэффициент испарения; т ij ( t ) — содержание феромона на участке I i j ; A_T ij ( t ) — приращение на каждой итерации, рассчитываемое по формуле:

Ат ij (t) = Е (K х (/(xp^jF p >  f(x j ,y_i + _x , _J + _x,   -- ,                       (14)

p = 1

где K — коэффициент прироста феромона.

Испарение происходит в связи с тем, чтобы было рассмотрено все пространство возможных решений.

При f(x,y)i+1j+1 > f(x,y)ij переход на участок Ii+1 ,j+1 с участка /,j запрещен. Таким образом, условие останова считается выполненным, если все муравьи не имеют возможности двигаться. В результате через N итераций муравьи займут ячейки с наименьшим значением функции, локализовав минимумы.

На основе описанного алгоритма и моделей (12, 13) разработано ПС, реализующее поиск локальных и глобальных экстремумов. В качестве примера на рис. 5 приводятся результаты поиска глобального и локальных минимумов ФР. Для решения выбраны границы области определения ФР, аналогичные принятым в предыдущих разделах. Выделенная область изначально делилась с шагом 0,25, и в каждом фрагменте помещалось по 2 муравья. Коэффици- енты a = 1, в = 0,5, Р = 0,5, K = 1 и т = 1. На рис. 5 изображены отдельные этапы работы ПС.

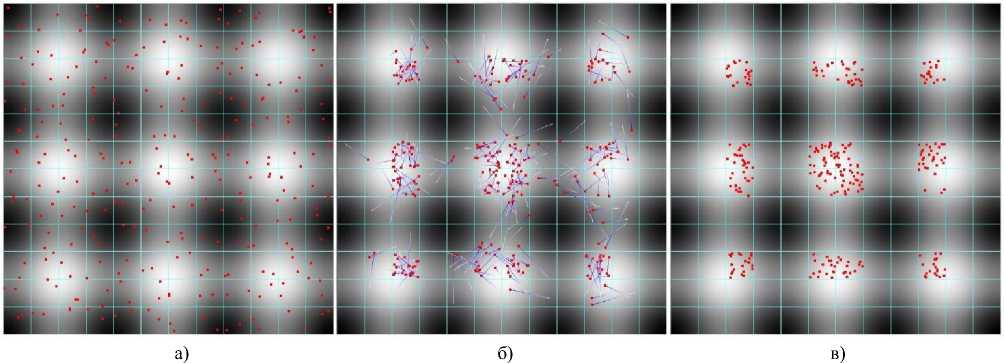
Рис. 5. Визуализация этапов работы ПС: инициализация (а); 3-я итерация (б); финальный результат (в)

Уже после трех итераций наблюдается повышение концентрации агентов во всех областях минимумов функции. Финальный результат получен за 6 итераций. На рис. 5, в видно, что агенты не только обнаруживают все минимумы, но и выделяют их значимость своим количеством.

Рассмотрим пример применения алгоритма с большим разбиением исследуемой области. Данный алгоритм применяется повторно к локализованным участкам до тех пор, пока не будет получен результат с заданной точностью. На рис. 6 отображены полученные за 220 итераций результаты локализации и двух уточнений глобального экстремума с разбиением 100x100 участков, который располагается в точке (0, 0). Такой результат получен в связи с исходными данными и особенностями строения ФР.

а)                                                   б)                                                в)

Рис. 6. Результаты локализации и уточнения при разбиении области 100x100: выделение всех локальных экстремумов (a);

выделение наилучшего локального экстремума (б); уточнение глобального экстремума (в)

В заключение стоит отметить, что при относительно малом количестве итераций МА дает прекрасные результаты, что свидетельствует о его эффективности при МЭ оптимизации функций.

Заключение . Для исследования эффективности решения задачи оптимизации при многоэкстремальности объекта были выбраны три эвристических алгоритма. Анализ результатов их использования показал, что данные методы действенны и эффективны, хотя есть существенные различия между структурами процессов поиска и между формами оценки получаемых результатов. Эти свойства алгоритмов определяются в каждом конкретном случае специфическими подходами к решению задачи: обнаружение и идентификация локальных экстремумов, способы кластеризации и последующие операции уточнения результатов. Тем не менее, во всех случаях оказалось необходимым подвергнуть каждый из этих методов существенной модификации, связанной с необходимостью кластеризации данных. Исследования показали, что каждый метод может обеспечить практически любую требуемую точность решения экстремальной задачи (наилучший результат: МРЧ = 1,94E-06; ЭГА = 5E-06; МА = 3,75E-07). Это, конечно, обусловливает значительное увеличение вычислительных и временных ресурсов. Однако применительно к исследуемой тестовой функции все методы показали вполне приемлемую производительность (средние затраты времени на эксперимент: МРЧ ≈ 300 с; ЭГА ≈ 86 с; МА ≈ 128 с). Таким образом, все три исследованных в данной работе метода актуальны и перспективны. Конкретный выбор алгоритмического инструмента для решения той или иной МЭ задачи зависит от опыта и от личных предпочтений исследователя, а также от специфических характеристик предметной области исследования.