Экспериментальное изучение температурной зависимости капиллярного движения жидкости в пористых средах с помощью метода акустической эмиссии

Введение. Зависимость динамики поднятия жидкости по капилляру от различных параметров теоретически и экспериментально изучалась многими авторами [1-3]. В задачах капиллярной гидродинамики важно правильно оценить скорость заполнения капилляров, в том числе время движения жидкости до остановки и скорость старта жидкости в начале заполнения. Подобные проблемы встречаются в различных отраслях промышленности и, в частности, в химических технологиях. Так, в работе [3] численным методом решалась задача заполнения цилиндрического капилляра проводящей жидкостью, в результате чего было установлено время и стартовая скорость заполнения капилляра. Численно можно решить полученное нелинейное уравнение капиллярного движения жидкости, используя современные вычислительные методы на базе компьютерных технологий. Однако в этом случае сложно анализировать зависимость полученного решения от параметров задачи. Наиболее варьируемым технологическим параметром в различных отраслях химической технологии была и остается температура процесса. Целью настоящей работы являлось изучение температурного вклада в динамику пропитки пористых материалов.

Современное состояние вопроса. Основой для проведения расчетов динамики капиллярного заполнения пористых сред является известная зависимость Жюрена, определяющая высоту поднятия жидкости в капиллярах. Чем меньше радиус капилляра R, тем на большую высоту h поднимается в ней жидкость (рис. 1). Высота поднятия столба жидкости растет также с увеличением коэффициента поверхностного натяжения жидкости:

капилляра, м.

Чем больше радиус капилляра, тем меньше высота подъема жидкости. При повышении температуры увеличивается радиус капилляра, что, в свою очередь, сказывается на скорости подъема жидкости h=f(t), причем на начальной стадии скорость продвижения жидкости по капилляру выше для случая большего радиуса. Поскольку предполагается, что для одних и тех же капилляров сохраняется соотношение R=f(T), то качественно вышеприведенный график не изменится.

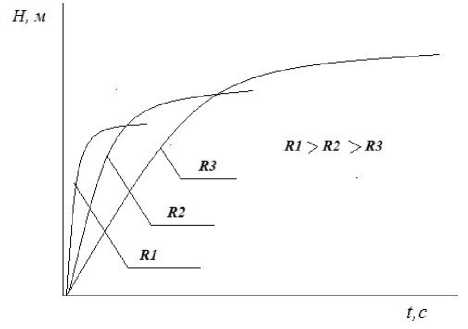
Рис. 1. Изменение высоты (А) капиллярного поднятия жидкости от времени (/) при использовании капилляров различного радиуса

С другой стороны, в известных выражениях, связывающих высоту и скорость подъема жидкости по капилляру с радиусом капилляра, фигурирует величина поверхностного натяжения. И с ростом температуры эта величина также будет меняться. Более того, можно высказать предположение, что именно изменение величины поверхностного натяжения окажется доминантным в выражениях, связывающих динамику поднятия жидкости по капилляру с температурой. Единственной силой, поднимающей жидкость вверх по капилляру против силы тяжести, является сила адгезии между жидкостью и стенками капилляра, и эта сила распределена вблизи поверхности капилляра.

Незначительное изменение температуры (на 5-10°С) практически не сказывается на диаметре капилляра (коэффициент линейного расширения большинства тел находится в диапазоне 1x10-2--6/град), т.е. изменение температуры на 10°С скажется лишь на уровне в 1x10"L -5 от измеряемой величины (высота и скорость подъема жидкости по капилляру). В то же время известно, что сила адгезии между жидкостью и стенками капилляра от температуры может существенно поменяться, поскольку от температуры зависят как вязкость жидкости и величина поверхностного натяжения жидкости, так и лиофильность (лиофобность) материала капилляра, определяющие краевой угол смачивания.

Сложность учета в формуле Жюрена температурных зависимостей величины поверхностного натяжения жидкости, изменения краевого угла смачивания, плотности жидкости практически исключают аналитическое вычисление динамики капиллярного заполнения пористых сред при изменении температуры. Именно поэтому, в силу компликативности факторов, определяющих температурную зависимость высоты и скорость подъема жидкости по капилляру, все теоретические изыскания ограничиваются изучением геометрии капилляра. Изучено влияние формы капилляра (цилиндрические и щелевые), влияние отклонения радиуса мениска от формы идеального круга [3], но значительно менее подробно теоретически изучено влияние реологии жидкости и поверхностно -активного взаимодействия системы «жидкость — твердое тело» на высоту и скорость подъема жидкости по капилляру. Этому вопросу в основном посвящены не теоретические, а экспериментальные исследования.

Экспериментально изучать капиллярное заполнение пористых материалов можно различными способами. В настоящей работе впервые был использован метод акустической эмиссии. Основанием использования именно этого метода для диагностики скорости капиллярного заполнения послужил известный эффект «прыжков Хейнса» [4, 5]. При объемном капиллярном течении в гофрированном 195

капилляре мениск вынужден периодически растягиваться и сжиматься соответственно в расширениях и сужениях капилляра. При этом мениск принимает форму, далекую от равновесной. Такие места мениск проходит очень быстро. Это явление получило название «прыжки Хейнса». Они обусловлены флуктуацией давления в жидкости при пропитке и дренаже и сопровождаются соответствующей диссипацией энергии. Если существование эффекта «прыжков Хейнса» было замечено достаточно давно, то характеристики спектра шума в жидкой среде были получены сравнительно недавно [6, 7].

Физическая картина явления такова: внедрение в пористый объект жидкости порождает растущий перколяционный кластер, расширение которого происходит нерегулярными скачками, связанными с заполнением карманов пор с большим радиусом (по сравнению с радиусом узкого горлышка, соединяющего карман с кластером). Это порождает регистрируемый в ультразвуковом диапазоне «шум», который является одним из проявлений метода акустической эмиссии.

Ввиду того, что сигналы АЭ отражают динамику продвижения жидкости по капилляру, априорно можно высказать предположение, что высота капиллярного подъема жидкости коррелирует с количеством индуцированных при этом сигналов АЭ.

Установлено, что при прочих равных условиях с увеличением радиуса капилляра несколько увеличивается скорость поднятия жидкости на начальном этапе, но значительно уменьшается максимальная высота (табл. 1).

Таблица 1

Экспериментальные данные по измерению скорости капиллярного поднятия 95% спирта по стеклянным капиллярам различного диаметра

Диаметр капилляра, мм	Время, с	Высота поднятия, м	Скорость поднятия, мм/с
0,31	0,92	0,031
	2,23	0,041	7,633
	4,21	0,051	5,051
	7,47	0,061	3,067
	13,07	0,071	1,785
	23,23	0,081	0,984
	49,4	0,088	0,382
0,34	1,07	0,03
	2,13	0,04	9,433
	3,99	0,05	5,376
	7,72	0,06	2,681
	11,41	0,065	2,710
	27,72	0,0711	0,62

Для наглядности эти экспериментальные данные представлены на рис. 2. Как видно из приведенного графика, полученные экспериментальные данные качественно воспроизводят картину динамики капиллярного подъема жидкости: на начальной стадии процесса скорость подъема жидкости в капилляре с большим радиусом более высокая (9,433 мм/с против 7,633 мм/с), однако, итоговая высота подъема меньше (0,0711 м и 0,088 м соответственно).

Методика эксперимента. Керамический образец (в нашем случае алюмооксидный носитель а- А 2 С 3) подвешивался в жидкость таким образом, чтобы кромка образца соприкасались с уровнем жидкости, обеспечивая капиллярную пропитку.

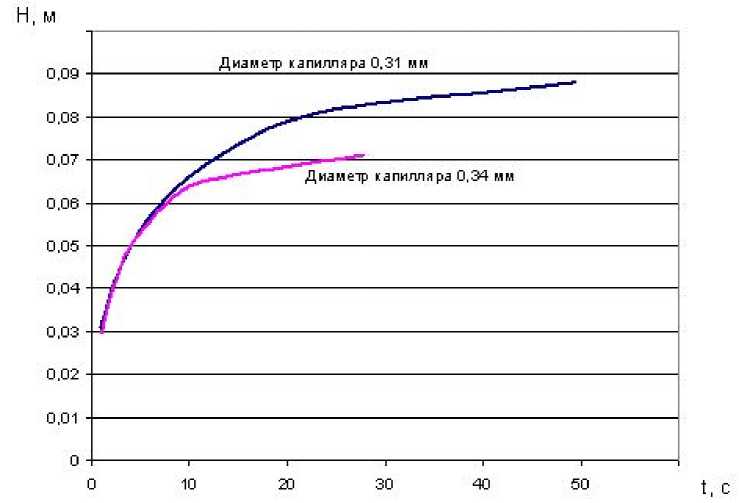
Рис. 2. Экспериментальные данные по измерению скорости капиллярного поднятия 95% спирта по стеклянным капиллярам различного диаметра

В процессе пропитки индуцируемые волны АЭ достигали стенок ёмкости и воспринимались чувствительным пьезодатчиком. Форма ёмкости выбиралась таким образом, чтобы обеспечить усиление регистрируемого сигнала. Материалы ёмкости представлял собой кварц, который характеризуется ). -- эмиссионных событий и позволяет проводить параллельно до 8 экспериментов.

Частотный диапазон используемых пьезодатчиков составлял 100-500 кГц. Выбор именно такого - чен для регистрации сигналов акустической эмиссии (АЭ), вызванной гидродинамическими и (или) аэродинамическими явлениями при протекании жидкости или газа через сквозную несплошность объекта. Методика регистрации сигналов АЭ в жидких средах подробно рассмотрены в целом ряде работ [8

метры АЭ, как суммарный счет сигналов АЭ и активность АЭ.

Что касается погрешности измерения параметров АЭ, то выбор измеряемого параметра АЭ

- контроля определяется целью контроля. При этом необходимо выбирать измеряемую величину, дающую максимум информации, удобную для выделения и обработки, устойчивую по отношению к возмущающим факторам. Наиболее применимыми параметрами можно считать статистические закономерности распределения параметров АЭ во временной области. При этом ранее проведенными работами установлено, что кривая изменения суммарного счета импульсов АЭ при измерении процессов

импрегнирования может быть описана уравнением общего вида N = K (1- e ). Величина относительной случайной погрешности составляет менее 0,1 %, погрешность измерения максимальной амплитуды АЭ сигнала — ± 0,5 дБ [8]. Следует указать, что в данной работе учитывалась динамика изменения абсолютной и относительной случайной погрешности при измерении активности АЭ и сум- 197

маркого счета АЭ, а также воспроизводимость метода (суммарное количество импульсов АЭ отличается на значение, составляющее до 10% измеряемой величины).

Центральная информационно -вычислительная станция

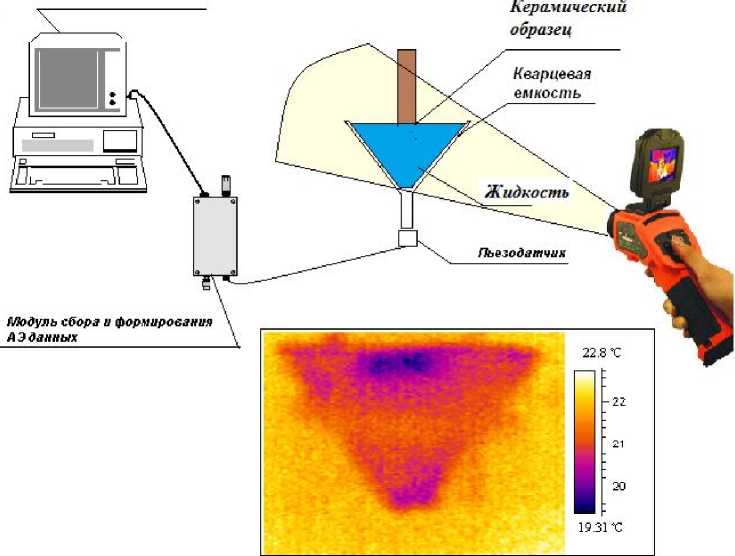
Рис. 3. Схема эксперимента по изучению температурной зависимости капиллярного движения жидкости в пористых средах с использованием методов АЭ и тепловизионного контроля

Образцы перед началом и после окончания пропитки взвешивались, с точностью до 1x10-3 г. Температура жидкости и пропитываемого керамического образца измерялась дистанционно с помощью тепловизора SATHOTFIND (рис. 3) абсолютная погрешность измерения температуры которым составляет ± 0,1°С.

Обсуждение экспериментальных данных. Проведенные эксперименты показали, что наиболее информативными параметрами АЭ, отражающими динамику капиллярного поднятия, являются сумма сигналов АЭ (ЛО и сумма осцилляций (выбросов) АЭ (М7 Форма кривой изменения суммы сигналов АЭ и суммы выбросов АЭ совпадает с формой кривой динамики изменения высоты подъема жидкости по капиллярам керамического образца, построенной по экспериментальным данным (табл. 1). Однако даже незначительное изменение температуры достаточно существенно меняет численные параметры кривой, что, впрочем, не сказывается на характере функции — она все равно остается экспоненциальной. Таким образом, можно констатировать, что параметры АЭ объективно отражают процесс капиллярной пропитки и по мере увеличения высоты капиллярного поднятия жидкости интенсивность процесса снижается.

В то же время скорость снижения интенсивности капиллярного поднятия оказалась высокочувствительной по отношению к температуре процесса. Рост температуры воды с 43 до 62°С привёл к снижению суммарной величины /Vпрактически в два раза (с 1800 импульсов до 960 импульсов). Причиной этого может являться увеличение диссипации механической энергии акустических колебаний в окружающую среду и, как следствие, — снижение энергии, амплитуды и длительности полезного сигнала, воспринимаемого пьезодатчиком.

Наиболее существенно это сказалось на параметре «выбросы N» (количество осцилляций, превышающих установленной уровень дискриминации в период нахождения огибающей электрического импульса АЭ над порогом ограничения). Если длительность сигналов в среднем снизилась также примерно в два раза (рис. 4), среднее значение амплитуды — на 10%, то количество осцилляций — в шесть раз (с 20x10³ до 120x10³).

Представленные данные отчетливо показывают разницу в характере протекающих процессов капиллярного поднятия жидкости при разных температурах, рис. 4.

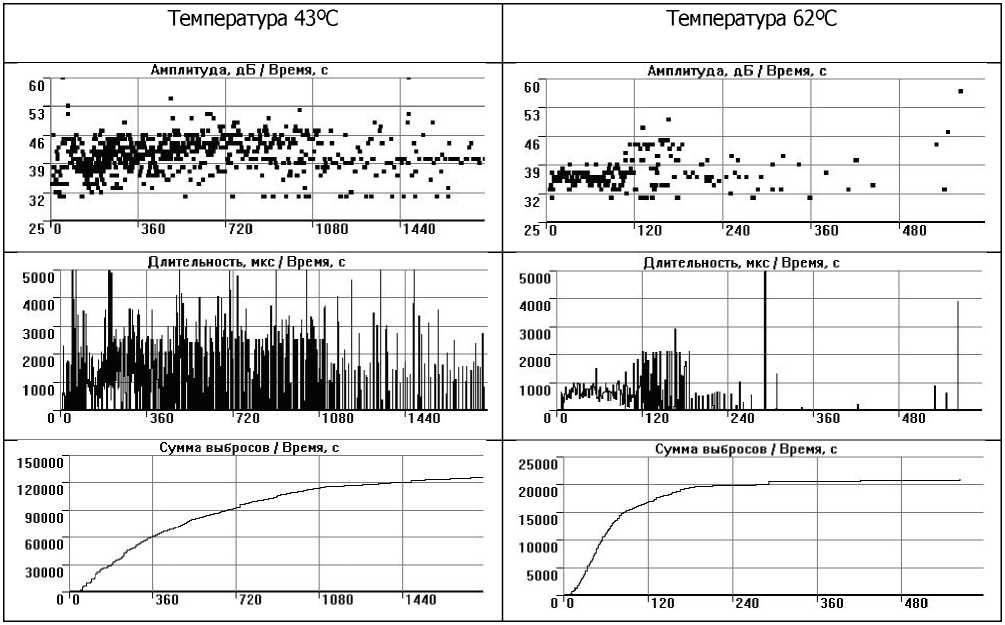
Рис. 4. Изменение ряда параметров АЭ при повышении температуры пропитки керамического образца

В начале капиллярного поднятия активность АЭ (количество сигналов АЭ в единицу времени) повышается при повышении температуры. Следовательно, наклон кривой суммарного количества импульсов АЭ по отношению к оси абсцисс значительно больше. Причина этого в физике процесса — при более высокой температуре смачиваемость жидкостью поверхности выше, следовательно, и адгезия лучше. Процесс капиллярного движения также отражает разницу в величине поверхностного взаимодействия жидкости и твердого тела и сил поверхностного натяжения жидкости. Чем выше эта разница, тем меньше радиус мениска и тем быстрее подъем жидкости по капилляру. И, наоборот, в случае превышения значения силы поверхностного натяжения жидкости над величиной поверхностного взаимодействия жидкости и твердого тела мы наблюдаем отрицательный мениск и снижение уровня жидкости в капилляре (случай не смачиваемого твердого тела). Таким образом, кривая суммарного счета импульсов АЭ показывает, насколько лучше смачивается тело при повышении температуры и насколько быстрее идет процесс капиллярного поднятия. Тот факт, что с ростом температур и затухание сигналов АЭ выше также свидетельствует о многофакторности процесса: увеличение диаметра 199

капилляра, увеличение диссипации энергии акустических сигналов в окружающую среду — все это приводит к более быстрому насыщению кривой N=f(r).

Заключение. Снижение суммарного числа сигналов АЭ при увеличении температуры пропитки полностью вписывается в описание кинетики капиллярного поднятия. Для случая химически инертного материала по отношению к импрегнату (в нашем случае — дистиллированная вода) изменение высо-

-

Пуазёйля и формулой Жюрена. Поскольку капиллярное заполнение пор с переменным сечением неизбежно вызывает акустическую эмиссию (эффект Хейнса), следовательно, параметры АЭ отражают

- свою очередь, открывает новые возможности применения метода АЭ, например, изучение объемного температурного коэффициента расширения пористых тел.