Экспериментальное определение характеристик сопротивления усталости изделий авиационной техники

Усталостное разрушение металлов наиболее опасно, поскольку в условиях отсутствия пластической деформации, «сигнализирующей» о приближающейся опасности, разрушение происходит внезапно и может привести к катастрофе. Все это приводит к необходимости расширения круга вопросов, подлежащих исследованию.

Как правило, характеристики сопротивления усталости материалов определяют путем испытания при различных уровнях напряжений серии одинаковых лабораторных образцов или деталей из одного материала [1, 2].

В зависимости от требований к точности и полноте получаемых характеристик либо применяют обычную методику построения кривой усталости по результатам небольшого числа образцов (до 10), либо испытывают большее количество образцов (50-100), и по результатам испытаний строят полные вероятностные диаграммы усталости.

В данной работе приведен расчет характеристик сопротивления усталости как по обычной методике построения кривой усталости (рассмотрены результаты испытаний 8 образцов среднего участка лопасти вертолета), так и по методике проведения испытаний большего числа образцов (84) с последующей вероятностной трактовкой результатов испытаний. В первом случае кривые усталости построены в полулогарифмических координатах. Кривые усталости аппроксимируют двумя прямыми линиями наклонной в диапазоне N = 8,8 • 106(lg(N) = 6,5) до N = 50 • 106(lg(N) = 7,69) и при N > 50 • 106 циклов. Во втором случае диаграммы усталости представляют собой семейство кривых распределения усталостной долговечности в координатах: вероятность P(%) - число циклов до разрушения lg(N) с параметром oa ; напряжения oa -стью P(%); разрушающие напряжения у б разрушения N.

число циклов до разрушения lg (N ) с вероятно - вероятность P(%) при различных циклах до

Наблюдения за амплитудой колебаний образцов производились по мерному клину, который устанавливался, по возможности, в месте наибольших амплитуд колебаний образцов. Растягивающая статическая подгрузка на образцах задавалась таким образом, чтобы в них возникали напряжения, предусмотренные программой испытаний. После задания растягивающей статической подгрузки, образцы нагружались знакопеременными изгибающими моментами, с уменьшением их ступенями через каждые 2 мм амплитуды по мерному клину. Начальная амплитуда напряжений, при которой возникают переменные напряжения и переменные изгибающие моменты в контрольных сечениях образцов, задана программой испытаний для соответствующего режима испытаний. Число ступеней равно 3. Запись напряжений на каждой ступени производилась по 3 раза. По среднеарифметическим значениям замеренных напряжений строились графики зависимости переменных напряжений в контрольных точках образцов от амплитуды колебании, которая записывалась в течение всего периода испытаний. В напряженных сечениях образца возникают напряжения, изменяющиеся по симметричному циклу. Для обеспечения точности поддержания режима испытаний в пределах требований программы испытаний через каждые 15 мин производился контроль амплитуды по мерному клину с занесением результатов в журнал испытаний. Контроль статической подгрузки производился через каждые 10 млн. циклов. При измерениях переменных напряжений использовался комплекс тензометрической аппаратуры. Пределы выносливости были определены на базе 20 • 10⁷ циклов по формулам

X у 6 N

У» = 6--- i—^L или M = 6

ww

\ 20 • 106                \ где уi - напряжения на i -ном режиме испытаний; Mi

X M i ⁶ N i 20 • 10⁶

,

- изгибающие моменты на i -ном ре-

жиме испытаний; N - наработка циклов на i -ном режиме испытаний. Приведенная наработка циклов для образцов среднего участка

N пр = X N pi

г \⁶

V у Й 7

,

где N_pi - наработка циклов в разрушившемся сечении на i -ном режиме испытаний; у _Pi - напряжения в разрушившемся сечении на i -ном режиме испытаний; у й - заданное программой переменное напряжение в контрольном сечении.

Заданное программой напряжение равно уд = 5,5 • б, у 5 я + у 5 + у 6 я + у 6

где коэффициент б = —---5---1---6 . Модуль упругости для образцов среднего участка у 3 a + у 3 + у 4 a + у 4

алюминиевого сплава равен 0 , 72 • 10⁵ МПа.

Для построения кривой усталости по обычной методике проводили испытания 8 образцов. На рисунке 1 представлены результаты образцов среднего участка лопасти при растяжении-сжатии (симметричный цикл с коэффициентом R = -1) по оси абсцисс отложено число циклов lg (N), которые выдержали образцы до разрушения, по оси ординат - амплитуда пе- ременных напряжений уб(ММП. Образец №1, испытанный при амплитуде у а = 104,9 МПа, проработал до разрушения 3,3 -106 (lg(N) = 6,5) циклов (что соответствует ординате и абсциссе точки 1). Образец №2, испытанный при амплитуде уа = 100,6МПа, разрушился при числе циклов N = 4,2 -106 (lg(N)=7,68). Постепенное снижение амплитуды напряжений приводит к повышению долговечности образца, под которой понимается число циклов до разрушения образца (или до появления трещины заданных размеров). Так, образец №6 при амплитуде уа = 75,5МПа проработал до разрушения N = 48 -106 (lg(N)=7,68) циклов (точка 6). Образец №8 при амплитуде аа = 56МПа проработал без разрушения 51 -106циклов (lg(N)=7,7). В процессе более длительных испытаний было установлено, что в условиях нормальных температур и отсутствии коррозии (при обычных атмосферных условиях) образцы, не разрушившиеся при N = 51 -106 циклов, не разрушаются и далее.

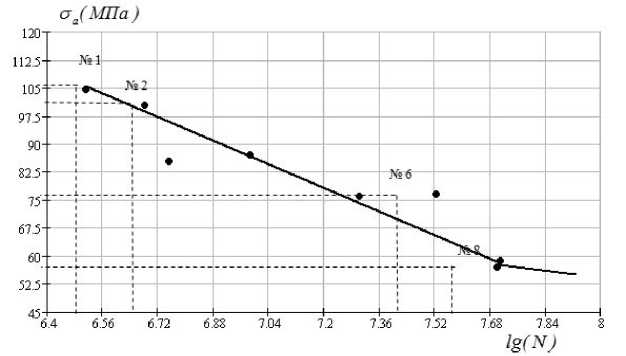
Рис. 1. Кривая усталости образцов среднего участка лопасти

Предварительно задаваемое число циклов напряжений, до которого образцы испытывают на усталость, называют базой испытания и обозначают N₆ . В данном случае это число равно N₆ = 51 - 10⁶ циклов. Амплитуда а а = 56 МПа , соответствующая середине интервала, обладает тем свойством, что при у а <  56 МПа образцы не разрушаются до базы испытания, а при а а >  56 МПа - разрушаются. Такое значение амплитуды напряжений при симметричном цикле называют пределом выносливости при симметричном цикле и обозначают а - 1 (индекс «-1» указывает на значение коэффициента асимметрии цикла). Таким образом, по результатам описанных испытаний найдено, что предел выносливости при симметричном цикле для образца составляет а - 1 = 56 МПа .

При испытании ограниченного числа образцов предел выносливости определяется как наибольшее значение максимальных (по величине) напряжений цикла, при действии которого еще не происходит образование усталостных трещин заданной протяженности или полного усталостного разрушения образцов до заданного числа циклов. Через экспериментальные точки (рис. 1) проведены наклонные линии, которые в совокупности образуют кривую усталости, или кривую Веллера.

Уравнение левого наклонного участка кривой усталости, изображаемой в полулогарифмических координатах прямой линией, имеет вид аа + K lg N = а-1 + K lg N0, (1)

где т - 1 - предел выносливости; N 0 - число циклов, соответствующее точке перелома кривой усталости, а N 0 =5Ь10⁶ (lg(N)=7,7) циклов, т _{- 1}=56МПа; К - коэффициент, характеризующий наклон левого участка кривой усталости.

Для определения коэффициента К необходимо, кроме т - 1 и N 0 , знать координаты одной точки наклонной линии. Например, на рисунке 1 в качестве таких координат могут быть взяты т _а =100,6МПа, N =4,3^10⁶ (точка 2). Тогда из уравнения (1)

K = у а -у -1 = 100,6 - 56 = 42,47_ lg N0 - lg N 7,7 - 6,65

Кривая усталости не имеет явно выраженного горизонтального участка и постепенно непрерывно снижается. При этом сопротивление усталости характеризуют пределом ограниченной выносливости т _{- 1 N} , под которым понимают максимальное напряжение цикла, соответствующее по кривой усталости числу циклов N . В этом случае кривую усталости аппроксимируют тогда двумя прямыми линиями в двойных логарифмических координатах, описываемыми уравнениями

Tm N = т mN0 N0 при та > т-1 n0 mm       , та 2 N = т-1N0 N0   пРи та < т-1N0

где т - 1 _Nq - предел ограниченной выносливости, соответствующий числу циклов N 0 , причем lg т - 1 _Nq и lg N 0 являются координатами точки пересечения указанных прямых; m 1 , m 2 - соответственно показатели углов наклона верхней и нижней частей кривых усталости.

Для описания указанных кривых усталости используют также уравнения Вейбулла: (Та - Т-1 „ )(N = N1)в = B , где N1, в, B - параметры уравнения; т , V - предел выносливости, соответствующий неограниченной базе (N= V.).

Для этой же цели предложено уравнение обобщенной кривой усталости, которая является общей для деформируемых алюминиевых сплавов при изгибе с вращением:

т = т - 1 + A [lg( N + N ^Г,

__ т _ т-1да         , где та = -a-; т-1 =----; N1, A, a - параметры уравнения; т'_1 - предел выносливости, т-1            т '-1

соответствующий базе N₆ = 5Ы0⁶ циклов.

Характеристики сопротивления усталости, такие как число циклов до разрушения N и предел выносливости при симметричном цикле, являются случайными величинами при ресурсных испытаниях среднего участка лопасти. Для изучения закономерностей рассеяния характеристик выносливости проводились испытания среднего участка лопасти по четырем режимам нагружения. Общее количество испытанных образцов n =84. По результатам усталостных испытаний большого числа идентичных образцов при одном уровне амплитуды напряжений получается большой разброс на долговечность. Такие характеристики сопротивления усталости, как число циклов разрушения N и предел выносливости т - 1 являются случайными величинами, поэтому можно говорить о статистической природе процесса усталостного разрушения.

Случайная величина Х характеризуется функцией распределения F(x) , определяющей вероятность того, что Х будет меньше, чем заданная величина х

F(x) = P(X < x), где Р(Х<х) - вероятность.

Вероятность событий Р - постоянное число, которое определяется отношением числа благоприятствующих данному событию исходов испытаний n ко всему числу возможных исходов испытания n _£ при n _£ ^ да

P = lim

Г n )

.

ⁿ £>' k ⁿ £ J

Функция F(x) возрастающая и стремится к единице с увеличением х до бесконечности. Если F ( x - ) = P ( X <  x ₁) и F ( x ₂) = P ( X <  x ₂), то вероятность попадания случайной величины Х в интервал x ₂ - x ₁ будет равна P ( x ₁ <  X <  x ₂) = F ( x ₂) - F ( x ₁). Так как первая производная от „ ,         „                        . dF ( x )

F(x) по х является дифференциальной функцией распределения f (x) =-----, то можем за- dx писать следующее выражение:

^x 2

^x 2

x ₂

P ( x 1 <  X <  x 2) = J f ( x ) dx - J f ( x ) dx = J f ( x ) dx.

-да

-да

^x i

Согласно вероятности Р число попаданий случайной величины в заданном интервале будет x 2

n ( x₁< X < x ₂ ) = n _£ P ( x₁< X < x ₂ ) = n _£ J f ( x ) dx =n _£ [ F ( x ₂ ) - F ( x ₁ )]. ^x i

Построим эмпирическую функцию распределения случайной величины Х=lg(N) и определим параметры этой функции методами математической статистики. Логарифмы полученных чисел циклов до разрушения располагают в возрастающем порядке, образуя, таким образом, вариационный ряд, служащий исходной информацией для статистической обработки и графического изображения функции распределения случайной величины. Для получения параметров функций распределения долговечности проводим статистическую обработку исходной информации по методам В.П. Когаева [3]. Введем функции распределения случайной величины X = lg( N ) и расположим в возрастающем порядке, а именно в виде X 1 <  X ₂ < • • • <  Xn . На рисунке 2 представлена функция распределения долговечности среднего участка лопасти. По оси абсцисс откладываются значения X_t = lg( N i ) в равномерном масштабе, по оси ординат - оценки вероятности разрушения, вычисленные по формуле „ i — 0,5                                                                                             „

P =----- 100%, где n число образцов, испытанных при данном уровне нагружения. Такой

n график называется полной вероятностной диаграммой усталости.

При I режиме испытаний опытные данные аппроксимирует функция регрессии с использованием полинома второго порядка, которая в системе Mathcad реализует комбинацию встроенных функций регрессии (regress) и интерполяции (interp). При II режиме испытаний экспериментальные данные интерполирует сплайн-функция второго порядка (pspline). При III и IV режимах испытаний экспериментальные данные интерполирует линейная сплайн-функция (lspline). Общее количество испытаний равно n=28 . Величины i являются порядковыми номерами соответствующих значений lg(N). Среднее значение lg( N ) и среднеквадратичное отклонение S _lg ( _N ) случайной величины являются параметрами распределения.

Статистические оценки этих величин имеют значения n lg( N) = - Z lg( Ni) = 7,701;

ⁿ i . 1

^S lg( N ) =

n

— 2(lg( N i ) - lg( N )² = 0,0032. n - 1 7=1

Коэффициент вариации u _lg ( _N ) случайной величины lg( N ) равен u _lg ( _N ) = 0.00042.

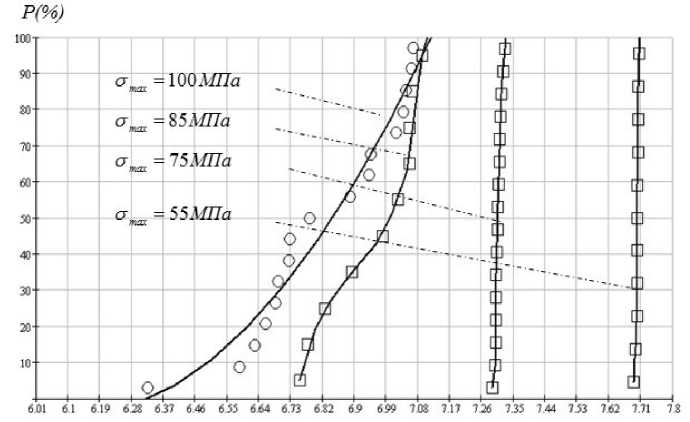
lg(N)

Рис. 2. Функции распределения долговечности образцов среднего участка лопасти из алюминиевого сплава при симметричном цикле

Полная вероятностная диаграмма усталости может быть представлена в виде семейства кривых усталости в координатах lg a max - lg N для различных вероятностей разрушения P (%) . Графики строятся следующим образом: проводя горизонталь на рисунке 2, соответствующую P (%) , получаем следующие значения a _max и lg( N ) для точек пересечения с линиями распределения. По полученным данным получаем кривые усталости образцов средней части лопасти из алюминиевого сплава, соответствующие различным вероятностям разрушения (рис. 2). Полная вероятностная диаграмма усталости может быть также представлена в виде функции распределения пределов выносливости в координатах P - a max по параметру числа циклов (рис. 3). Графики строятся следующим образом: проводя вертикаль на рисунке 2, соответствующую N , получаем следующие значения a _max и P(%) для точек пересечения с линиями распределения.

На рисунке 3 представлены зависимости параметров функций распределения пределов выносливости при различных числах циклов по нормальному закону распределения, а на рисунке 4 представлены параметры этих функций распределения пределов выносливости при различных циклах. Так, например, при N=5,2 10⁶ среднее значение выносливости а - 1 =85МПА получается по линии при u p = 0 (Р=50%). Квантили u p = 1 (Р=84%) соответствует значение ( a .1 ) _{u = 1} = 109 МПа . Отсюда следует среднеквадратичное отклонение S _a 1 = 24МПа. Предельное напряжение a _lim = 93,6 МПа - среднеквадратичное отклонение a               S                S„

S = 18,4 МПа.   При значениях n = ^^=1,1; v,. = -^ im =0,196;    v_n = ^ ;

lim ,                                                                                a lim                                a a                  a lim                  a u =__n -1 =0,29 получаем вероятность разрушения Р=61% [4].

p           ..2 ..2 ..2

\ v a lim n + v a

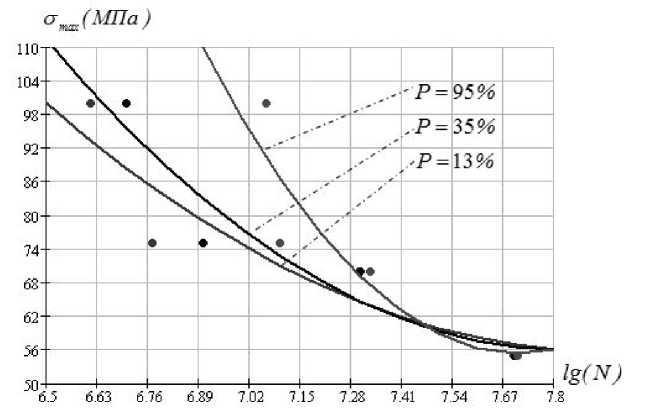
Рис. 3. Кривые усталости образцов среднего участка лопасти из алюминиевого сплава, соответствующие различным вероятностям разрушения

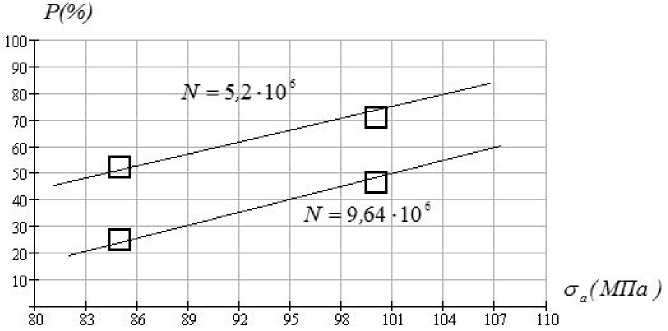
Рис. 4. Функции распределения пределов выносливости образцов среднего участка лопасти из алюминиевого сплава, соответствующие различным числам циклов

В данной работе определены характеристики сопротивления усталости конструкции лопасти несущего винта вертолета и приведены результаты контрольных испытаний образцов среднего участка лопасти несущего винта.