Экспериментальное определение параметров магнитного сердечника и катушки индуктивности на его основе

Довольно часто при проектировании силовых преобразователей электрической энергии стоит задача определения конструктивных параметров катушки индуктивности с сердечником на заданные параметры. Для этого необходимо иметь при расчетах его данные. Если они известны, то имеется возможность воспользоваться различными более или менее точными методиками в зависимости от их сложности [1–3]. Причем при использовании упрощенных методик повышается погрешность расчета, а при более точных моделях, основанных на расчете полевых задач, затрачивается дополнительное время и требуется дорогостоящее программное обеспечение [4, 5]. Если необходимые параметры сердечника неизвестны, возможность расчета проектируемого на нем дросселя вообще отсутствует. В этом случае остается применение экспериментального метода определения параметров. Он снимает описанные ограничения и дает возможность дальнейшего использования экспериментальных данных при расчетах.

Материалы и методы

Объектом исследования настоящей статьи является магнитная система на броневом сердечнике ГМ24ДС ШЛ 40 x 80 (100 x 40) ТУ 1261-03212287107-2010 фирмы «Гаммамет» [6, 7], на основе которой можно выполнить катушку индуктивности.

Применение конструкции данной катушки предполагается в схеме выпрямителя в составе LC -фильтра [8, с. 198] или в других цепях силовых схем технологического оборудования [10–12].

При постановке задачи для расчета катушки индуктивности в LC -фильтре обычно указывается максимальное и действующее значения тока I m , I d , а также необходимая индуктивность L .

Задача экспериментального исследования параметров заключается в измерении семейства кри- вых намагничивания Φ(F) – зависимости магнитного потока от магнитодвижущей силы (МДС) при различных зазорах δ между половинками магнитопровода [9]. Эти зависимости нужны для того, чтобы определить конструктивные параметры катушки: число витков w и зазор δ, необходимые для достижения требуемой индуктивности L при изменении тока вплоть до тока насыщения Im.

Для измерения зависимости магнитного потока Φ от МДС обмотки F необходимо сформировать в обмотке импульс тока, достаточный для насыщения магнитопровода [13]. Для данной цели была произведена намотка обмотки в центральной части магнитопровода проводом ПУВГ 1 x 4 мм 2 . Количество витков выбрано произвольно, поскольку для задания МДС важно лишь произведение тока и числа витков. Однако надо учитывать, что число витков влияет на коммутируемый ток, и небольшое значение числа витков может привести к перегрузке коммутирующего ключа. Первоначально число витков выбрано w = 11.

Для построения кривой намагничивания Φ( F ) в процессе формирования тока на каналы осциллографа в режиме XY должны быть поданы сигналы, пропорциональные Φ и F соответственно. При этом на экране осциллографа высветится искомая зависимость. Построение этой зависимости можно также производить постобработкой измеренных зависимостей Φ( t ) и F( t ) на ЭВМ [14, с. 389]. При этом измерение величин Φ и F производится косвенным методом.

Учитывая связь МДС F ( t ) и тока i ( t ) в обмотке [15, с. 350]:

F ( t ) = i ( t ) ■ w , (1)

измерение МДС можно провести по измерению тока. В свою очередь, ток можно определить по напряжению U Sh ( t ), измеренному с помощью токоизмерительного шунта с сопротивлением R Sh :

i ⁽ t ) =

U Sh ( t ) ,

R Sh  ,

и тогда (1) с учетом (2):

F ( t ) =

U Sh ( t ) --w .

R Sh

Измерение же магнитного потока Φ можно проводить двумя методами.

Метод 1. С помощью потокоизмерительной обмотки.

На центральный полюс магнитопровода устанавливается потокоизмерительная обмотка. Количество витков w 1 этой обмотки влияет на коэффициент связи между потоком Φ и напряжением U ₁ на ней [16].

Выходное напряжение U1 на измерительной обмотке связано с измеряемым потоком, пронизы- вающим контур витков:

U 1

d Ф

= w ---.

1 dt

Тогда для определения временной зависимости потока Φ(t) напряжение U1(t) необходимо про- интегрировать:

Ф ( t ) = C U ^-) dt .

w ₁

Это преобразование можно провести постобработкой напряжения U 1 ( t ) на ЭВМ и затем построить зависимость Φ( F ). В случае если нет возможности провести обработку результатов, можно на выход потокоизмерительной обмотки установить RC -интегрирующую цепочку [17, с. 34; 18, с. 17], напряжение U ₂( t ) на выходе которой:

и 2 ( t ) =      J u 1 ( t ) dt .                          (6)

RC

При этом постоянная времени τ = RC для получения более точного интегрирования должна быть намного больше, хотя бы на порядок, чем время импульса напряжения U 1 ( t ).

Таким образом, выражая Φ( t ) через U 2 ( t ):

RC

Ф ( t ) =---- U 2 ( t ).

w ₁

Как видно из (3) и (7), напряжения пропорциональны измеряемым величинам F(t) и Φ(t), что позволяет получить на экране кривую намагничивания.

Метод 2. С использованием эквивалентной схемы замещения катушки индуктивности.

Из схемы замещения напряжение U LR на выводах катушки можно записать [19]:

t/ф

U lr ( t ) = R L i ( t ) + -- = R L i ( t ) + w-- ,      (8)

dt               dt где RL – активное сопротивление обмотки катушки, i(t) – ток в катушке, Ψ – потокосцепление обмотки, Φ – поток в среднем полюсе, w – число витков обмотки.

Сопротивление R_L достаточно точно может быть измерено омметром, и тогда для определения зависимости Φ( t ) из (8):

Ф ( t ) = J U LR ⁽ t ) - R L i ⁽ t ) dt. w

Эту операцию можно провести постобработкой данных по измеренной зависимости i ( t ).

В экспериментальном исследовании за основу выбран второй метод, поскольку он не требует сборки дополнительных цепей и производится по непосредственному измерению тока на шунте и напряжения на обмотке.

Важным вопросом экспериментального исследования является формирование тока i ( t ). При уровне токов в сотни–тысячи ампер это представляется весьма проблематичным при использовании в качестве источника стандартной электрической сети. Предлагается для формирования мощных импульсов тока использовать тиристорноконденсаторную схему, которая представлена на рис. 1 [20, 21]. Она позволяет получить двуполярный одиночный импульс тока, амплитудное значе-

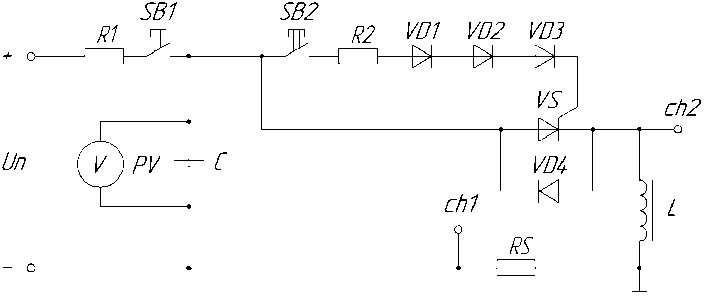
Рис. 1. Тиристорно-конденсаторная схема для определения параметров дросселя

Таблица 1

Перечень используемых электронных компонентов

Обозначение на схеме Описание R1 KNP-200 2 Вт, 100 Ом, 5 % R2 MO-200 2 Вт, 82 Ом, 5 % RS Ekits ШУНТ-10 А 75 mV C К75-100 2400 мкФ ± 10 % 1600 В 1302 ОТК SB1 Кнопка IEK APBB-22N Ue 230 В ~ SB2 Кнопка XB7-NA-1… VD1–VD3 IN4007 BL VD4 Быстровосстанавливающийся диод FR607 VS Estel сделано в СССР ТБ143-400-11-Н23 11-86 L Сердечник ГМ24ДС ШЛ 40x80 (100x40) ТУ 1261-032-12287107-2010. Провод ПУВГ 1x4 мм2. Количество витков w = 11 PV Мультиметр TEK DT9208A ние которого ограничивается типами тиристора и диода.

Работа схемы проходит в два этапа: заряда конденсатора и его разряда на обмотку.

На этапе заряда при разомкнутой кнопке SB 2 замыкается SB 1 и через ограничительный резистор R 1 конденсатор C заряжается до напряжения U_C = U _п, которое контролируется вольтметром PV . Затем, после полного заряда конденсатора, кнопка SB 1 размыкается. Схема готова к этапу разряда.

На этапе разряда при разомкнутой кнопке SB 1 замыкается SB 2, которая осуществляет подачу управляющего импульса на силовой тиристор VS через ограничительный резистор R 2 и диоды VD 1– VD 3, которые, в свою очередь, защищают управляющий переход тиристор от обратного напряжения. В результате подачи управляющего импульса тиристор открывается и разряжает через себя конденсатор C на нагрузку в виде исследуемой катушки индуктивности L . Обратный диод VD 4 используется для обеспечения пути перезаряда конденсатора. Каналами ch 1 и ch 2 осциллографа относительно общей точки схемы фиксируются ток дросселя (обратной полярности) с шунта RS и падение напряжения на дросселе U_L соответственно.

Экспериментальная установка собрана из элементов, указанных в табл. 1.

Выбор напряжения заряда должен осуществляться последовательным его увеличением до уровня, при котором по диаграммам тока наблюдается процесс насыщения магнитопровода. Этот процесс определяется по характерному изменению скорости нарастания тока на осциллограмме I ( t ). Однако для предотвращения выхода из строя тиристора и диода превышать допустимые токи не следует. Если насыщение в этом случае не произошло, то надо либо взять тиристор и диод с большим значением допустимого тока, либо увеличить обмотку еще на несколько витков, что при том же токе позволит получить большие значения МДС F .

В процессе экспериментальных исследований проводилась серия опытов с последовательным изменением зазора. При этом первый опыт был поставлен без немагнитных прокладок при сочленении магнитопроводов, а затем в каждом опыте зазор последовательно дискретно увеличивался немагнитными прокладками, изготовленными из стеклотекстолита толщиной 0,57 мм.

На рис. 2 для примера приведены зависимости тока I ( t ) и напряжения U ( t ) на катушке с двумя прокладками в немагнитном зазоре.

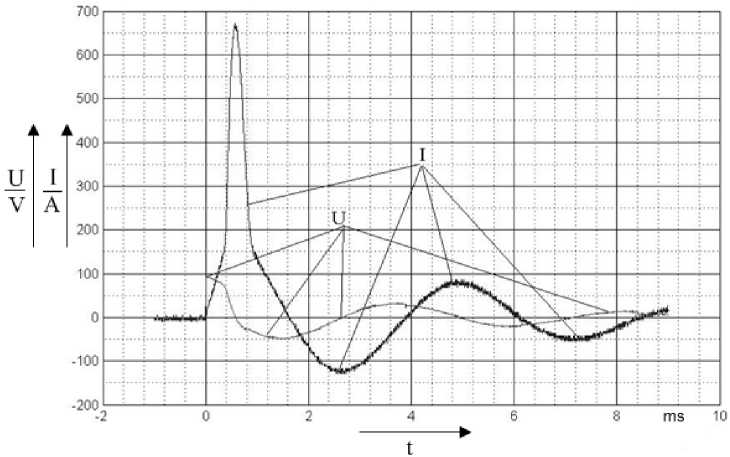
Рис. 2. Осциллограмма тока I ( t ) и напряжения U ( t ) на катушке с двумя прокладками в немагнитном зазоре

Сбор данных осуществлялся с помощью осциллографа Tektronix TDS 2024 C , соединенного с компьютером USB -кабелем. Передача данных для дальнейшей обработки в среде MATLAB осуществлялась через интерфейс GPIB , согласно инструкции [22]. Полученные в результате передачи данных файлы с расширением .mat обрабатывались программой в соответствии со следующим программным кодом:

clear all % Очистка всех предыдущих переменных close all % Закрывание всех открытых дополнительных окон

% Загрузка данных, записанных осциллографом

% Создание пустых переменных ch1, ch2, leg, dt ch1 = [];

ch2 = [];

dt = [];

leg = {};

for i=0:7

dt = [dt d.t(2)-d.t(1)];

end

% Задание значений и констант

N = 11; % Количество витков rL = 0.0174; % Активное сопротивление катушки

I = -ch1 / 0.0075; % Расчет значения тока, через шунт uL = ch2 - I*rL; % Расчет падения напряжения на индуктивности, представляя реальную катушку как последовательно соединенное активное сопротивление rL и индуктивность L.

% Выделение данных для отображения значений только в первом квадранте координатной плоскости, без повторения процессов при перезаряде for i=1:size(ch1,2)

[~,ind] = max(I(:,i));

ind = ind-1 + find(I(ind:end,i)<0, 1, 'first');

if ~isempty(ind)

I(ind:end,i) = NaN;

uL(ind:end,i) = NaN;

end end

% Интегрирование

Phi = cumsum(uL .* (ones(size(uL,1),1)*dt)); % расчет потокосцепления rr = 1:size(I,2); % Выбор номера загруженных файлов для построения графиков

% Построение графика figure plot(I(:,rr)*N, Phi(:,rr)/N) % Вывод значений МДС и магнитного потока xlabel('F [A]') % задание подписи оси x ylabel('\Phi [Вб]') % задание подписи оси y legend(leg{rr},'Location','SouthEast')

grid on grid minor

% Задание границ графика xlim([0 10000])

ylim([0 0.004])

б)

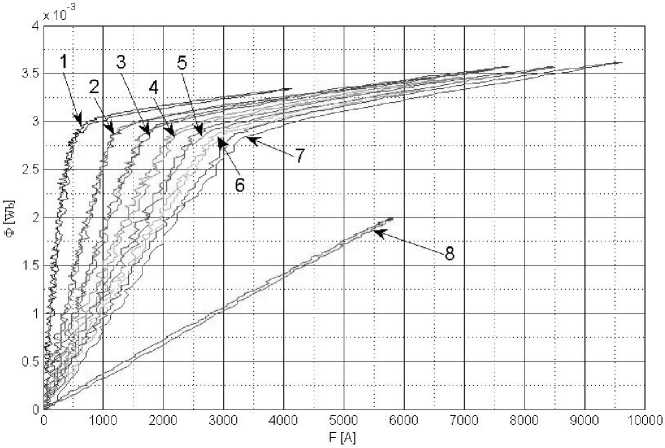
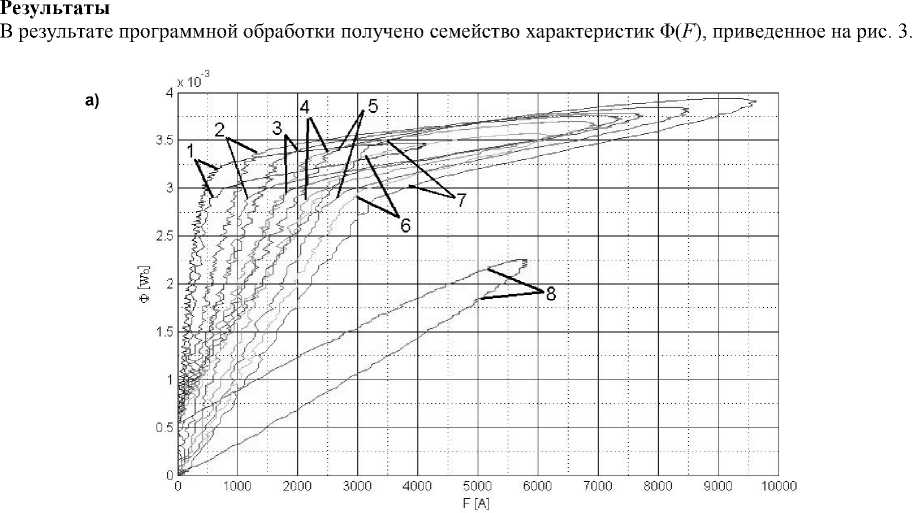
Рис. 3. Семейство кривых намагничивания Φ( F ) при различных зазорах δ между половинками магнитопровода: a – без учета R_L ; б – с учетом R_L . № 1 – δ = 0 мм; № 2 – δ = 0,57 мм; № 3 – δ = 1,14 мм; № 4 – δ = 1,71 мм; № 5 – δ = 2,28 мм; № 6 – δ = 2,85 мм; № 7 – δ = 3,42 мм; № 8 – без половины магнитопровода

Особенностями характеристик рис. 3 является наличие колебаний на их ветвях. Это связано с наличием электромагнитных помех при измерени-ии напряжения с токового шунта (рис. 2) (пропорционального МДС F ), так как он не подвергался по методике эксперимента фильтрации, как например, сигнал напряжения (пропорциональный магнитному потоку Ф). Однако в силу периодичности помехи и ее нулевого среднего значения построенные характеристики отображают общий вид реальных кривых намагничивания. Для более точного их отображения для сигнала с шунта можно применить высокочастотную фильтрацию или сгладить его математическими методами.

По рис. 3а и 3б наблюдаются существенные различия в площади, заключаемой кривыми, и форме зависимостей Φ( F ), если в расчетах учитывать или не учитывать измеренное активное сопротивление обмотки R_L = 0,0174 Ом. Характеристики намагничивания по рис. 3б визуально заключают в себе весьма малые площади. Это свидетельствует о малых энергиях потерь по сравнению с энергией, запасаемой в магнитном поле (площадь между осью Φ и соответствующей кривой намагничивания) на каждом такте перемагничивания. Площадь заключенная каждой кривой пропорциональна энергии потерь за время импульса перемагничивания (вихревых и перемагничивания). Неточность введения R_L при расчетах приведет к заметным ошибкам в оценке потерь в магнитопроводе.

Из анализа характеристик рис. 3 можно установить, что их излом (начало насыщения) происходит примерно при одном значении потока Φ m = 2,8 мВб. По экспериментальным данным заполнена табл. 2, в которой рассчитаны: МДС, при которой начинается насыщение F m , магнитная проводимость G , а также индуктивность катушки L . В случае кривой 8 измерение проводилось по линейному участку и в формулах вместо потока Φ _m и

МДС F m использовались значения координаты крайней точки на кривой.

Практический интерес представляет сравнение полученных индуктивностей с измерениями RLC -метром E 7-22 с абсолютной погрешностью не хуже 2 % [23]. Корректность этих измерений следует из того, что измерения прибором проводятся при небольших токах, далеких от насыщения. При таких токах характеристики катушки определяются в основном зазором и потому линейны. Результаты измерений приведены в табл. 2.

Из анализа погрешностей измерений следует, что в области меньших зазоров погрешность выше, чем в области больших. Поскольку чувствительность индуктивности к зазору при меньших зазорах выше, а измерения при снятии кривых и измерения RLC -метром производились в разных сериях опытов, то одинаковую точность выставления зазора обеспечить было невозможно. Поэтому измерения описанным методом подтверждены с погрешностью не более 8 %.

Указанные в табл. 2 данные можно использовать при проектировании катушки индуктивности с требуемыми индуктивностью L и током I m . В таком случае необходимо определить количество витков w и зазор δ, необходимые для достижения этих параметров.

Как было определено по характеристикам, переход к режиму насыщения независимо от δ ограничен определенным значением Φ _m . Тогда, используя связь Φ m и потокосцепления Ψ m через число витков w [24, с. 185, 189]:

^ m = L ■ I m = W ■Ф m , (10)

можно получить:

LI

W = ——

Ф

m

.

Максимальную МДС можно определить по формуле [15, с. 350]:

Таблица 2

Данные результатов опытов при различных зазорах исследуемого дросселя

Номер кривой Φ( F )	1	2	3	4	5	6	7	8
Количество немагнитных прокладок, шт.	0	1	2	3	4	5	6	Без половинки магнитопровода
Зазор δ, мм	0	0,57	1,14	1,71	2,28	2,85	3,42	–
Ток насыщения Im , А	50	105	151	191	227	260	282	–
МДС насыщения Fm , А	550	1150	1660	2100	2500	2850	3100	–
Магнитная проводимость G = Φ m / Fm , мкГн	5,09	2,42	1,68	1,33	1,12	0,98	0,9	0,35
Индуктивность L = w 2·Φ m / Fm , мкГн	616	293,33	203,97	161,26	135,68	118,46	109,22	42,35
Индуктивность, измеренная RLC -метром L RLC , мкГн	670	315,2	214	167,6	139,8	121	111,3	45,5
Относительное отклонение результатов X =( L RLC – L )·100/ L RLC , %	8,06	6,94	4,69	3,78	2,95	2,1	1,87	6,9

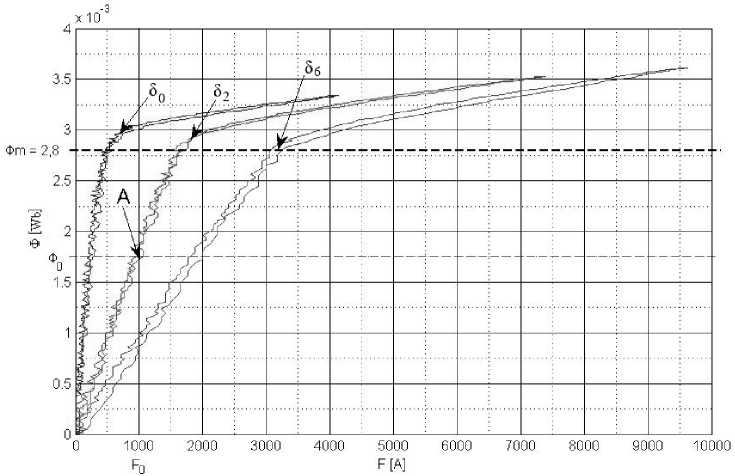
Рис. 4. Пример расчета параметров катушки индуктивности

F = I w m   m w ,

затем по характеристикам рис. 2, необходимо определить кривую, которой принадлежит точка ( F_m , Φ _m ), и ей соответствующий зазор δ. Далее необходимо проверить, может ли в окно сердечника быть установлена рассчитанная обмотка? Для этого необходимо определить площадь требуемого сечения S_p обмотки:

Sp = Idr, (13) j ■ k где k – коэффициент заполнения паза проводниками, j – плотность тока в обмотке, Id – действующее значение тока.

Если площадь Sp больше площади паза магнитопровода, то обмотку нельзя установить в магнитопровод. Это означает, что на данном магнито- проводе невозможно построить катушку с параметрами L и Id и следует выбрать магнитопровод с большим произведением сечения паза на сечение центрального полюса магнитопровода [25].

Данный расчет проведен исходя из условия намагничивания магнитопровода до насыщения. Если же расчет проводить с выбором w и δ таким образом, чтобы магнитопровод не входил в насы- щение, тогда при определенном количестве витков w по (11) необходимо в знаменатель подставить Φ0 несколько меньше, чем Φm, и определить ей соответствующий зазор δx.

Рассмотрим пример расчета при Φ _m = 2,8 мВб, Φ₀ = 1,75 мВб, L = 45 мкГн, I ₀ = 200 А.

Число витков по формуле (11):

w =

LI m

^ф о

45 Л0 ^{- 6} ■ 200

1,75 Л0-3

МДС при максимальном токе I 0 :

F₀ = 1 0 w = 200 ■ 5 = 1000 A.

На рис. 4 приведен пример нахождения требуемого зазора по характеристикам рис. 2.

Точка А с током I 0 , изображенная на характеристиках, соответствует 2-м прокладкам (δ х = 1,14 мм) в зазоре магнитопровода.

В общем случае при расчете точка может попасть между измеренными кривыми, тогда определение зазора необходимо проводить методами интерполяции [26].

Обсуждение

Указанная методика может быть применена для определения параметров разных типов магнитных сердечников, а приведенный расчет – для уточнения конструктивных параметров катушек индуктивностей на этих сердечниках.

Заключение

В результате описанного экспериментального исследования получено семейство характеристик Φ( F ) – магнитного потока от МДС, при различных зазорах δ между половинками магнитопровода ГМ24ДС ШЛ 40 x 80 (100 x 40) ТУ 1261-03212287107-2010 фирмы «Гаммамет» и определен его магнитный поток насыщения Φ m = 2,8 мВб.

Данные, полученные при исследовании, можно использовать для расчета катушки индуктивности на базе указанного магнитопровода. Методика и оборудование, представленные в статье, универсальны и могут применяться для других типов сердечников.

Приведенный оценочный расчет позволяет оценить параметры катушки индуктивности: определить зазор δ и число витков w дросселя для достижения заданной индуктивности L при известном токе дросселя I .