Экспериментальное определение режима течения при радиальном движении жидкости

Радиальное движение жидкостей реализуется в большинстве типов насосов, аппаратах химических и пищевых отраслей, водном транспорте, металлургии, теплоэнергетике, нефтегазовой отрасли. Характеристики движения жидкостей лежат в основе практической реа- лизации процессов в таких аппаратах, причем режим течения при определенных условиях может быть не только ламинарным или турбулентным, но и с разрывом сплошности потока, кавитационным. Актуальность определения режима течения связана с его влиянием на гидравлические, энергетические и эксплуатационные характеристики различных устройств и систем.

Для характеристики кавитационных режимов течения обычно пользуются различными безразмерными параметрами, наиболее важным из которых является число кавитации, выра- жающее отношение сил давления к силам инерции:

^{2 (} p - p „ ) ^х       р V ^{2     ,}

где p – давление набегающего потока, Па; p н – давление насыщенных паров жидкости при температуре потока, Па; ρ – плотность среды, кг/м³; V – скорость потока на входе в систему, м/с.

Применение расчетных критериев в процессах с радиальным движением жидкости с учетом кавитации вызывает ряд трудностей, связанных, в частности, с определением полей скоростей, давлений и локальных плотностей жидкости.

При экспериментальном изучении возникновения и развития кавитации используют следующие методы [1]:

• а)    визуальные и слуховые методы наблюдения;

• б)    фотографирование и высокоскоростная съемка;

• в)    гидравлические методы, основанные на изменении параметров потока (расхода, скорости, перепада давлений и т.п.);

• г)    акустические методы;

• д)    электрические (омические, электроемкостные);

• е)    радиоактивные.

Тем не менее существует ряд ситуаций, когда ни один из имеющихся методов не может быть применен по тем или иным причинам.

Экспериментальные результаты

В данной работе для определения кавитационного режима предлагается использовать анализ зависимостей, аналогичных кривым текучести в координатах скорость – напряжение сдвига в реологии. Определение таких реологических характеристик проводят для веществ различного рода с применением ротационных вискозиметров [2]. По сути, такой прибор является гидродинамическим аппаратом с радиальным движением жидкости. Используя известные формулы [3] определения сдвигающего напряжения т, Па, и скорости сдвига D r , с^-1, для такого аппарата можно записать

= zM

^Т 2п IR

„ _ 2^ю R²

r = R2 — rX ’ где z – численная постоянная используемого экспериментального устройства; М – момент на валу привода аппарата, Нм l - ширина основания вращающейся мешалки, м; R - радиус мешалки, м; Гх - текущий радиус мешалки, м; и - угловая скорость, с-1.

При работе в режимах, не сопровождающихся нарушением сплошности потока, отношение сдвигающего напряжения к скорости сдвига должно быть равно известному для исследуемой

τ жидкости значению динамической вязкости η= , Па∙с. В кавитационном режиме течения

r из-за нарушения сплошности потока произойдет снижение плотности и, как следствие, уменьшение момента на валу привода аппарата, что будет соответствовать снижению величины η и изменению профиля кривой текучести.

Для исследования реологических характеристик сплошного и кавитационного потока была разработана экспериментальная установка. Установка собрана на базе лабораторного блендера с двигателем постоянного тока и регулятором частоты вращения, герметичной камеры и вакуумного насоса (рис. 1).

В вертикальной цилиндрической емкости установлена мешалка, представляющая собой двухлопастную клиновидную крыльчатку. Для предотвращения образования воронки в

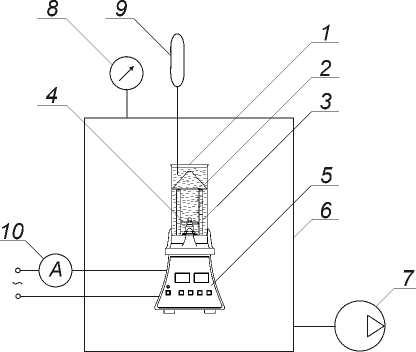
Рис. 1. Схема экспериментальной установки: 1 – рабочая емкость; 2 – конусная вставка; 3 – отражательные перегородки; 4 – двухлопастная клиновидная крыльчатка; 5 – привод лабораторного блендера; 6 – герметичная камера; 7 – вакуумный насос; 8 – вакуумметр; 9 – термометр; 10 – амперметр

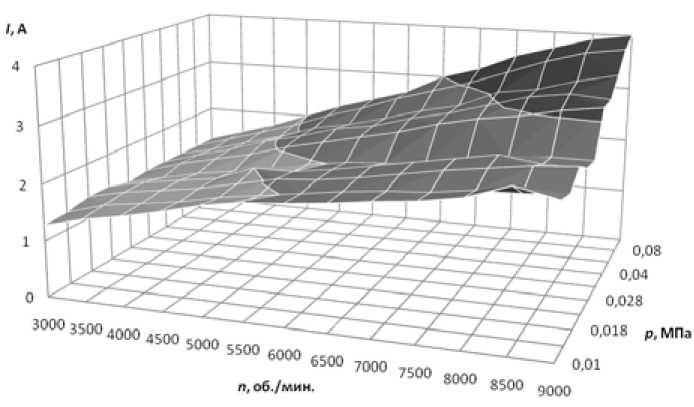
Рис. 2. Зависимости затрачиваемой мощности от числа оборотов и давления в установке емкость была помещена конусная вставка и три вертикальные отражательные перегородки, установленные перпендикулярно движению потока. В качестве рабочей жидкости взята отстоянная водопроводная вода, которую заливали в емкость перемешивающего аппарата. По ходу эксперимента в установке создавалось необходимое разряжение, затем происходил плавный набор скорости вращения до заданного числа оборотов. Опыты производили в диапазоне изменения абсолютного давления от 0,1 до 0,01 МПа при частоте вращения от 3000 до 9000 об/мин. В качестве выходного параметра снимали значение силы тока на приводе установки. Каждая экспериментальная точка снималась несколько раз на свежей порции воды. Результаты эксперимента представлены графически на рис. 2.

Анализ полученных данных

Физические условия, созданные в экспериментальной установке, гарантировали наличие режимов течения, характеризующихся нарушением сплошности потока. Это проявляется наиболее наглядно для случая, когда давление в вакуумной камере существенно отличается от атмосферного. Для дальнейшего анализа из массива полученных данных были выбраны значения, соответствующие атмосферному давлению (рис. 3, верхняя кривая) и максимальному разряжению p = 0,01 МПа (рис. 3, нижняя кривая).

Преобразуя известные формулы расчета механических характеристик двигателя постоянного тока согласно (2) – (3), можно связать величину потребляемой электрической мощности с реологическими характеристиками. Момент на валу электродвигателя пропорционален потребляемому току, следовательно, можно записать:

τ

~

, 2 • I k п 1R2

где I – потребляемый ток; А, k – коэффициент преобразования, зависящий от характеристик электродвигателя установки, электронного регулятора частоты вращения и геометрии гидродинамической части установки. В качестве характерного радиуса для подстановки в (3) была выбрана середина вращающейся лопасти (rx = 2 R), так как именно там происходит зарождение кавитационных полостей, что подтверждается результатами экспериментов. Место локализа- ции начальной стадия кавитации на движущейся лопасти представлено на рис. 4.

Обрабатывая экспериментальные зависимости с учетом сказанного, получаем кривые текучести (рис. 5).

Полученные зависимости показывают, что при течении в области сплошного потока скорость сдвига близка к линейному закону, это соответствует реологическим параметрам тече-

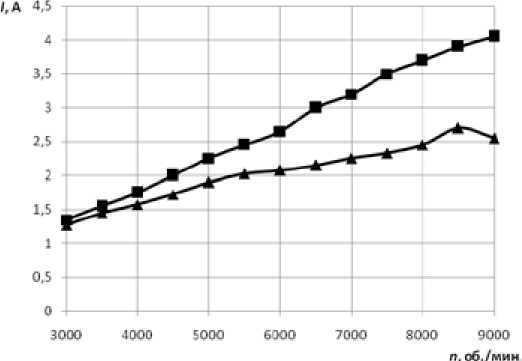
Рис. 3. Зависимость величины тока от числа оборотов: ■ – p = 0,1 МПа; ▲ – p = 0,01 МПа

Рис. 4. Место локализации начальной стадия кавитации на движущейся лопасти

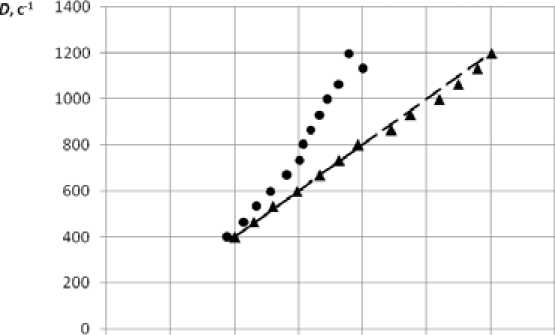
О 200    400    600    800   1000   1200   1400 т.Па

Рис. 5. Зависимость скорости сдвига от сдвигающего напряжения: • - p = 0,01 МПа; ▲ - p = 0,1 МПа; ----кривая текучести ньютоновской жидкости ния ньютоновской жидкости (рис. 5, нижняя кривая). Кривая, лежащая выше, описывает неньютоновский характер течения, что свидетельствует об изменении свойств потока.

Таким образом, изменение режима течения может быть зарегистрировано по изменению реологических параметров, а именно переходу от линейной зависимости скорости сдвига от сдвигающих напряжений D = f (т) к нелинейной форме.

Для определения параметров, при которых случается такой переход, были определены величины тангенса угла наклонов прямых, проходящих через начало координат D - т и каждую точку, полученную по результатам обработки экспериментальных данных. Из полученного массива выбраны точки, вблизи которых идет отклонение от известного значения вязкости для ньтоновской жидкости (рис. 6).

На рис. 6 нанесены кривые, соответствующие посчитанным по (1) числам кавитации. Область перехода режима течения от сплошного к кавитационному находится в диапазоне 0,8 <  х< 1,6 . Несовпадение формы аппроксимирующей экспериментальные точки кривой с кри- – 52 –

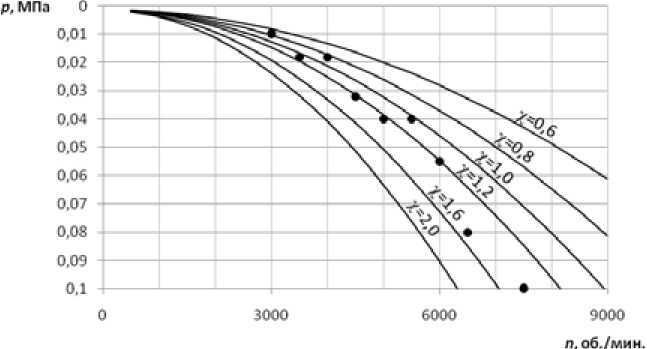
Рис. 6. Зависимость режима течения от числа оборотов и давления в установке выми постоянных чисел кавитации можно объяснить сложностью применения формулы (1) для радиального движения жидкости и погрешностью эксперимента.

Полученная номограмма позволяет определить режим течения в гидродинамическом аппарате в широком диапазоне изменения давлений и скоростей с достаточной для технологического использования точностью. Зависимости, подобные приведенным на (рис. 6), могут быть получены без явного использования реологических характеристик, а только по изменению тангенса угла наклона в координатах I-n (рис. 2).

Выводы

Предложена конструкция экспериментальной установки, позволяющей проводить исследования радиального движения жидкостей в кавитационном и докавитационном режимах в широком диапазоне скоростей и давлений окружающей среды. Разработан и апробирован метод, позволяющий по изменению сдвигающего напряжения и скорости сдвига определить режим течения при радиальном движении жидкости.