Экспериментальное определение сопротивления излучения конденсаторной антенны

Как известно [1-2; 6 и др.], сопротивление излучения RΣ антенны является производной величиной (коэффициентом пропорциональности) от мощности излучения PΣ и тока IA в точках питания. Рассмотрение сопротивления излучения бывает удобно использовать для комплексной характеристики излучающих (приемных) 2PV свойств антенны: Ry=^. В большинстве случаев величина RΣ определяется расчётным путём, что удобно для простейших линейных антенн, для которых выведены теоретические выражения.

Так, для короткого (l < 0,1λ) тонкого линей- ного вибратора-диполя в вакууме [1-2]

f iv

где l – длина половины проводника симметричного вибратора; λ – длина волны излучения; k = 2 π / λ – волновое число.

У реальных симметричных диполей сопротивление излучения в точках пучности тока носит колебательный характер в зависимости от отношения к длине волны и в частном случае при l/λ = 0,25 (полуволновой тонкий вибратор) имеет значение R_Σ ≈ 73,1 Ом.

Рассмотренные в [3-5] конденсаторные С-антенны имеют геометрические размеры, соответствующие условию применения выражений (1), и с точки зрения короткого симметричного вибратора-диполя имеют сопротивление излучения незначительной величины, не более нескольких Ом, что обусловливает их низкую эффективность к излучению (приему) ЭМВ при стандартном питании.

В то же время при использовании схемы и конструкции С-антенны, описанной в [3-4], утверждается, что при соблюдении определенных принципов и соответствующей настройке возможно получение при габаритных размерах антенны ( l < 0,1 λ ) сопротивления излучения значительной величины (десятки, сотни Ом). Целью данной статьи является экспериментальное измерение сопротивления излучения С-антенны посредством эквивалента антенны для подтверждения или опровержения теоретических и практических выводов, сделанных в [3-5].

Методы измерения сопротивления излучения антенны

Прямое экспериментальное измерение сопротивления излучения антенн связано с необходимостью измерения тока питания антенны I_A и мощности излучения P_Σ . Если при измерении I_A не возникает затруднений, то с непосредственным замером P_Σ , чаще всего возникают значительные трудности, особенно на невысоких частотах. Поэтому чаще всего P_Σ измеряют косвенно по известной характеристике направленности антенны и величине напряженности поля в волновой зоне, см. например [6].

Существует другой косвенный метод измерения R_Σ , когда антенну заменяют ее эквивалентом. Тогда при равенстве тока I_A в антенне и в ее эквиваленте, достигаемом изменением параметров эквивалентной схемы, принимают активное сопротивление эквивалента равным сопротивлению излучения, см. рис. 1. Ток в антенне удобнее измерять не непосредственно, а через входное сопротивление антенны на рабочей частоте (в диапазоне частот). Наиболее подходят для таких измерений антенные анализаторы или панорамные измерители коэффициента стоячей волны ( КСВ ). Тогда схему измерений можно изобразить как на рис. 2.

Порядок измерения R_Σ по схеме рис. 2 состоит в следующем:

• -    при установлении переключателей на входные зажимы антенны снимают зависимость КСВ либо X_A и R_A от частоты вблизи рабочей частоты антенны;

• -    устанавливают переключатели на вход эквивалента антенны и подбором величин параметров L, C, R добиваются максимального совпадения вида графика зависимости КСВ ( X_A ; R_A ) от частоты для исследуемой антенны и эквивалента антенны;

• -    отключают эквивалент антенны от схемы и измеряют омметром сопротивление переменного резистора, которое и принимается равным сопротивлению излучения исследуемой антенны.

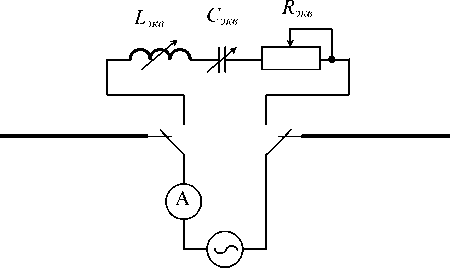
Рис. 1. Схема измерения сопротивления излучения с помощью эквивалента антенны

SWR

Рис. 2. Схема измерения сопротивления излучения с помощью эквивалента С-антенны и антенного анализатора

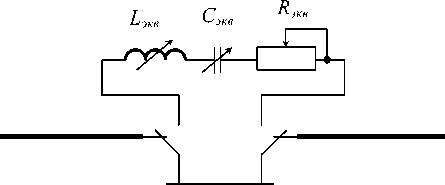
Для измерения данным методом R_Σ конденсаторной С-антенны, представляющей собой «раскрытый» контур с сосредоточенными параметрами, см. рис. 3, схема измерений упрощается.

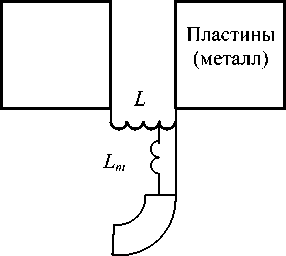
Рис. 3. Схема конденсаторной С-антенны

Пластины «раскрытого» контура представляют собой в эквивалентной схеме конденсатор, а катушка индуктивности остается общей для С-антенны и эквивалента, см. рис. 4.

(2 , Кэкв

ГП

L

Рис. 4. Схема подключения эквивалента конденсаторной С-антенны при измерении сопротивления излучения

Порядок измерений R_Σ конденсаторной С-ан-тенны остается таким же, как и в схеме по рис. 2. Обозначенная на рис. 3-4 катушка индуктивности

L_m применяется в С-антенне для улучшения согласования входа антенны и фидера (генератора) и позволяет более точно компенсировать реактивность во входном сопротивлении и в общем случае может отсутствовать.

Результаты эксперимента

Для экспериментального исследования R_Σ конденсаторной С-антенны была изготовлена антенна со следующими параметрами: центральная рабочая (резонансная) частота 30,3 МГц; размеры пластин раскрытого конденсатора 90×94 мм² при расстоянии между пластинами 30 мм; расчетная емкость между пластинами С = 1,77 пФ, полученная по формуле [7]:

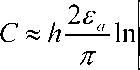
4(1+2^) d

где ε_а – диэлектрическая проницаемость среды, Ф/м; l и h – длина и высота пластин, м; d – расстояние между пластинами, м.

Общая, с учетом паразитных составляющих, «контурная» емкость С-антенны

с0 — С+СL.

Собственная емкость катушки C_L рассчитывалась согласно [8]:

1 =-------Т^’     (4)

где D – диаметр катушки в см; а = т!d^; do и т – диаметр и шаг обмотки. При D = 3,2 см; d ₀ = 1,5 мм; τ = 1,9 мм получим C_L = 3,9 пФ.

Тогда согласно (3) получим контурную емкость С₀ = 1,77 + 3,90 = 5,67 пФ. Поскольку расчетная резонансная индуктивность контурной антенной катушки

для С₀ = 5,67 пФ получаем L = 4,87 мкГн.

Рассчитанные согласно [8] конструкционные параметры контурной катушки L таковы: провод диаметром d =1,5 мм, N = 13 витков; D = 32 мм, отвод от 1,5 витка.

Согласующая катушка L_m имела следующие конструкционные параметры: провод d_m = 0,7 мм; N = 3 витка; D_m = 9 мм, что соответствует согласно [8] значению L_m ≈ 0,1 мкГн (как вариант может отсутствовать).

Таблица 1. Полоса частот 1KF при различных КСВ для С-антенны и эквивалента

КСВ		1,3	1,5	2,0	2,3
INF, МГц	С -антенна	0,48	0,92	1,44	1,8
	Эквивалент С -антенны	0,56	1,16	1,48	1,8

Таблица 2. Зависимость минимального КСВ эквивалента С-антенны от В_ЭК6 на частоте Fo

Вэкв, Ом	0	20	40	70	122	183	248	376
KCBmi„	2,1	1,76	1,5	1,3	1,12	1,3	1,5	2,0

а)

б)

Рис. 5. Зависимость КСВ от частоты а) для С-антенны; б) для ее эквивалента

В качестве анализатора SWR в схеме измерений по рис. 2 использовался панорамный измеритель КСВ типа РК2-47. Полученные наиболее близкие характеристики зависимостей КСВ от частоты для С-антенны и ее эквивалента приведены на рис. 5, где вторая снизу линия соответствует уровню КСВ = 1,3. При различных уровнях КСВ сравнительные полосы частот для С-антенны и эквивалента приведены в таблице 1

Изображенная на рис. 5б зависимость получена при величине эквивалентного сопротивлении излучения R_Σ = R_экв = 122 Ом. Была измерена зависимость минимального значения КСВ от величины эквивалентного сопротивления антенны, R _экв в диапазоне от 0 до 376 Ом при поддержании резонансной частоты F₀ . Полученные результаты представлены в таблице 2. Из таблицы 2 видно, что при КСВ < 1,3 значение R_экв = 70 … 183 Ом.

Сравнение сопротивлении излучения, полученного методом эквивалента и рассчитанного по измерению полосы частот излучения С-антенны

Посмотрим, как согласуется найденное экспериментально значение R_Σ = R_экв с помощью эквивалента С-антенны с предложенным в [9] расчетным значением, определяемым по радиотехническим формулам как эквивалентное активное сопротивление контура на резонансной частоте. Добротность контура на резонансной частоте можно выразить как [10]

w

R.4

где WA – волновое сопротивление С-ан-тенны; на частоте резонанса имеет место rz™ 1

i 77" —   77 — Xc ’ RA – активное сопро- тивление контура при резонансе; L1 – индуктив- ность последовательной ветви катушки антенного контура в эквивалентной схеме С-антенны (см. рис. 5 в [3]); co0 = 2ttF0 – круговая резонансная частота контура; XC – реактивное сопротивление конденсатора контура.

С учетом принятого условия, что RA = RΣ – то есть сопротивление излучения численно равно актив- ному сопротивлению эквивалентного контура при резонансе, а также с учетом того, что добротность контура С-антенны зависит от полосы частот эквивалентного контура [10] , имеем из (6) следующее выражение для RΣ :

Xr 2XF 2XF

Fo 2л Co Fo где 2ΔF – полоса частот пропускания (излучения) антенного контура по уровню –3 дБ.

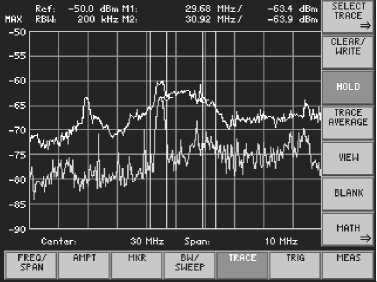
Рис. 6. Поле ЭМИ конденсаторной С-антенны

Заметим, что полоса пропускания 2Δ F контура С-антенны определяется по уровню поля электромагнитного излучения (ЭМИ) –3 дБ от максимума. Для ее определения была измерена напряженность Е -составляющей поля С-антенны с помощью измерительной установки, аналогичной приведенной на рис. 6 из [3]. На рис. 6 представлен снимок экрана анализатора спектра R&S FS300, где верхний график – ЭМИ С-антенны совместно с фоновым ЭМИ в лаборатории, нижний график – отдельно фоновое ЭМИ в лаборатории.

Из рис. 6 определяем полосу частот по уровню –3 дБ от максимального значения поля ЭМИ, 2Δ F ≈ 2,3 МГц (две крайние вертикальные линии), на том же рисунке для справки показана полоса излучения С-антенны при значении КСВ = 2,0 (две средние вертикальные линии).

При подстановке в (7) экспериментальных данных из рис. 6 и параметров антенны (3) получим R_Σ = 70,3 Ом. Из (7) также видно, что R_Σ сильно зависит от общей контурной емкости С-антенны, причем паразитная емкость (в основном межвитковая емкость контурной катушки) может быть больше дифференциальной емкости пластин. Влияние соотношения этих емкостей на параметры С-антенны представляется предметом дальнейших исследований. Также можно сделать вывод, что с увеличением контурной емкости снижается добротность С-антенны и увеличивается ее рабочая полоса по ЭМИ и КСВ .

Выводы

Для исследуемой конструкции С-антенны наилучшее согласование на частоте F ₀ на эквиваленте антенны имеет место при R_экв = 122 Ом (при КСВ_min = 1,12). Допустимое согласование при сохранении полосы пропускания около 2Δ F = 1,4 МГц по уровню КСВ = 2 обеспечивается при R_экв = 70 … 183 Ом. Можно предположить, что диапазон эквивалентного сопротивления излучения R_Σ составляет 70-183

Ом – при этом сохраняются приемлемые параметры С-антенны по излучению. Расхождение экспериментальных измерений R_Σ с помощью эквивалента С-антенны и расчетно-экспериментальных по полю ЭМИ можно объяснить неучтенной погрешностью макета и измерений и влиянием неидеальных условий в лаборатории по фоновому ЭМИ. Получено на порядок большее значение сопротивления излучения, чем это прогнозируется для аналогичных (малых по отношению к длине волны) симметричных дипольных антенн согласно (1), что подтверждает как практические, так и теоретические результаты и выводы [3-5] о высокой эффективности конденсаторных С-антенн.