Экспериментальное определение укрупненных первичных параметров линии электропередачи трехпроводного исполнения

Передача электрической энергии от места ее генерации к месту ее потребления выполняется при посредстве линий электропередачи (ЛЭП) различных исполнений. К отдаленным от места генерации электрической энергии потребителям энергия передается обычно по ЛЭП высокого и сверхвысокого напряжения чаще всего трехпроводного исполнения. Для прогнозирования и оценивания результатов передачи электрической энергии по ЛЭП от источника к потребителю необходимо иметь точные сведения о параметрах этих линий.

Параметры ЛЭП делятся на первичные и вторичные.

Первичные параметры – это параметры электрической схемы замещения ЛЭП: сопротивления, проводимости, электрической емкости, индуктивности.

Вторичные параметры – это постоянные распространения волн электромагнитного поля, волновые сопротивления, постоянные интегрирования, фазовые скорости и т. п. Для их определения необходимы сведения о первичных параметрах ЛЭП.

Методика исследования

Традиционно численные значения первичных параметров ЛЭП подбираются из соответствующей справочной литературы [1, 2]. Достоверность полученных таким образом сведений о первичных параметрах ЛЭП невелика. Но их обычно оказывается достаточно для ориентировочного представления о результатах передачи электрической энергии, соответствующей требованиям ГОСТ 32144–2013 [3].

Считается, что более достоверные сведения о первичных параметрах ЛЭП можно получить из аналитических выражений, которые приведены в специальной литературе [4–13]. И это действительно так, если пользователь сумеет правильно учесть все факторы, влияющие на передачу электрической энергии. А их множество, и их учет представляет собой трудоемкую задачу, не всегда обеспечивающую оперативность получения достоверных результатов.

В таком случае экспериментальное определение первичных параметров ЛЭП с привлечением элементов теории многополюсников оказывается достаточно перспективным. Применение элементов теории многополюсников уже неоднократно предлагалось использовать и используется для определения режимных параметров электроэнергетических объектов [14–16].

Трехпроводные ЛЭП целесообразно представлять именно восьмиполюсниками. Тогда применяемую здесь теорию многополюсников можно конкретизировать и назвать теорией восьмиполюсников.

Речь идет об определении первичных параметров однородного участка ЛЭП, в котором продольные и поперечные параметры по всей его протяженности неизменны. Но вся линия электропередачи в принципе не может быть однородна. Она может быть представлена в виде совокупности множества однородных участков. А каждый из этих участков может быть представлен в виде восьмиполюсника. Таким образом, получается цепная схема.

Для прогнозирования результатов передачи электрической энергии по такой ЛЭП следует оценить работу каждого однородного участка согласно теории восьмиполюсников, предварительно экспериментально определив численные значения коэффициентов каждого из них, а полученные таким образом данные обобщить на всю линию электропередачи [17–19]. Это громоздкая, трудоемкая процедура, которая связана с серьезными организационными и техническими сложностями.

Предлагается всю ЛЭП вместе с сопутствующей линейной арматурой объединить в единый восьмиполюсник. В таком случае для анализа его функционирования, а значит, анализа передачи электрической энергии по всей ЛЭП будут применимы все известные методики с той лишь разницей, что здесь должны использоваться укрупненные первичные и вторичные параметры.

Укрупненные вторичные параметры рассчитываются по известным методикам [18–23], в которых должны участвовать укрупненные первичные параметры. Укрупненные первичные параметры по своей сути являются параметрами восьмиполюсника, объединяющего все однородные участки анализируемой ЛЭП совместно с сопутствующей линейной арматурой.

Укрупненные первичные параметры следует определять экспериментально [18, 21, 24].

Для определения этих параметров для анализируемой ЛЭП следует выполнить опыты короткого замыкания и холостого хода. Но прежде эту ЛЭП следует представить укрупненной Г-образ-ной схемой замещения, как показано на рисунке. На этом рисунке представлена схема для выполнения серии экспериментов, необходимых для определения первичных параметров ЛЭП, состоящей из нескольких однородных участков.

В качестве источника электрической энергии для выполнения указанной серии экспериментов следует использовать источник трехфазной ЭДС пониженного напряжения. Кроме того, в экспериментах должны участвовать коммутационные аппараты S1–S9, установленные так, как показано на рисунке. К входным и выходным клеммам анализируемой ЛЭП должны быть подключены электроизмерительные приборы (вольтметры, амперметры, фазометры), обеспечивающие косвенное измерение комплексных значений входных и выходных напряжений и токов.

Опыт короткого замыкания позволяет определить укрупненные продольные параметры исследуемой ЛЭП. Для этого замыкаются ключи S 1– S 3 и S 7– S 9. При этом во избежание аварийной ситуации напряжение источника электрической энергии должно быть понижено.

При выполнении этого опыта напряжение на выходе анализируемой ЛЭП будет отсутствовать:

т'т - т'т — ТТ - п

U 2 Аk = U 2 Bk = U 2 Ck = 0 .

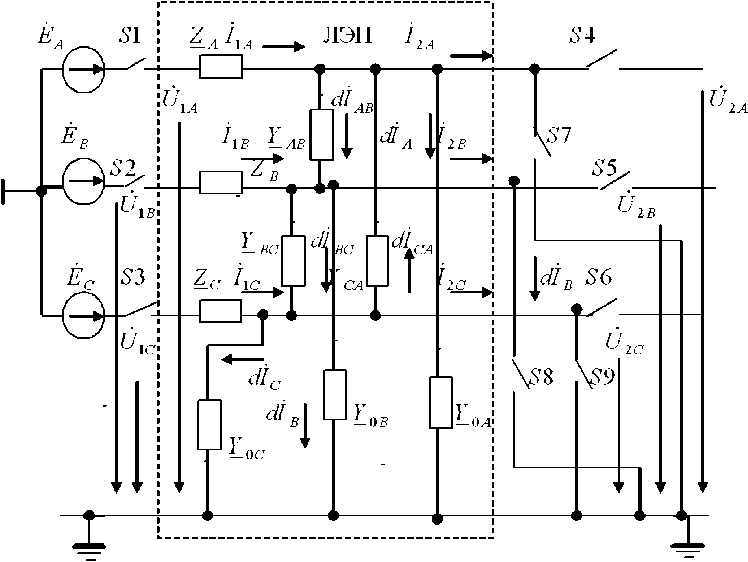
Схема серии экспериментов для определения укрупненных первичных параметров трехпроводной ЛЭП

В таком случае будут справедливы равенства: т'т

Za = _T ;                                   (1)

I 1 Ak

t't

U 1 Bk

Z B = T ;

I 1 Bk

ZC =

•

U 1 Ck

T .

I 1 Ck

Для выполнения опыта холостого хода необходимо разомкнуть ключи S 4– S 9, а ключи S 1– S 3 оставить в замкнутом состоянии (см. рисунок). В результате таких мероприятий будут справедливы уравнения:

T                    _i_TT

^U 1 Ax + 1 1 Ax Z A + ^U 2 Ax = 0;

- U 1 Bx + 1 1 BxZb + U 2 Bx = 0; *

U K - ⁺ I 1Cx^ZA ^{+ U} 2 Cx = 0.

Равенства (1)–(3) позволяют определить фактические укрупненные продольные параметры ЛЭП.

Укрупненные активные сопротивления линейных проводов определяют вещественные части их укрупненных полных сопротивлений:

R a = Re ( Z a ) ; (4)

Из этих уравнений получаются равенства, по-

зволяющие определить укрупненные продольные

Rb = Re ( Zb );

Rc = Re (Zc ).

Укрупненная индуктивность каждого линейного провода анализируемой ЛЭП определяется так:

параметры линии:

TT

ZA = U1 Ax ' U2 Ax ;(

I 1 Ax

TT

7  _ U1 Bx U2 Bx ,

ZB =     •       ;

I1Bx t’t t’t

ZC = UiCx • U2Cx .(12)

I 1 Cx

Затем из равенств (4)–(9) определяются ук-

LA

LB

LC

Im ( ZA ) .

2 n f ’ Im ( Z B ) .

2 n f ’

Im ( Z c )

2 n f ’

рупненные активные сопротивления и укрупненные индуктивности каждого линейного провода.

Равенства (10)–(12) можно получить и при подключении с помощью ключей S 4– S 6 электрической нагрузки.

Для определения укрупненных поперечных параметров ЛЭП, в состав которой входят не-

сколько однородных участков, следует выполнить

где f –

частота изменения напряжения и тока во времени.

В укрупненных индуктивностях, найденных при выполнении опыта короткого замыкания, учтены явления самоиндукции и взаимоиндукции, то есть учтены собственные и взаимные индуктивности. Так, в величине LA учтены собственная индуктивность линейного провода А и электромагнитное влияние индуктивностей соседних проводов В и С; в величине LB учтены собственная индуктивность линейного провода В и электромагнитное влияние индуктивностей соседних проводов А и С; в величине LC учтены собственная индуктивность линейного провода С и электромагнитное влияние индуктивностей соседних проводов А и В. Иначе говоря, в каждой укрупненной индуктивности из последних трех равенств учтены собственные индуктивности каждого линейного провода и взаимные индуктивности между соответствующими проводами.

Трехфазное короткое замыкание – достаточно тяжелый режим работы ЛЭП. Его выполнение может быть связано с техническими сложностями, связанными с техникой безопасности или другими техническими ограничениями. В таком случае этот режим (опыт) можно избежать, а продольные параметры ЛЭП можно определить и из опыта холостого хода.

серию экспериментов из трех опытов.

Первый опыт выполняется при замкнутых ключах S1–S3 и разомкнутых ключах S 4– S 6. Кроме того, должен быть разомкнут ключ S 7 и должны быть замкнуты ключи S 8 и S 9. В таком случае будут отсутствовать напряжения U _{2 B 1} и U _{2 C 1} , а также токи I _{2 A 1} , dI _{B 1} , dI _{C 1} и dI _{BC 1} :

^U 2 B 1 = ^U 2 C 1 = ⁰ ;

T — AT — AT —AT - П I 2 A 1 = ^dIB1 = ^dIC 1 = ^dIBC 1 = ⁰ .

При таких условиях справедливы уравнения:

t 1 t            it           1 t r\

1 1 A 1 ^{- dI}AB 1 ^{+ dI}CA1 ^{- dI}A1 = ⁰ ;

T । A T T — л -

1 1 B 1 ^{+ dI}AB1 I 2 B 1 = ⁰ ;

T AT T —

1 1 C 1 ^dICA1 I 2 C 1 = 0.

Из второго уравнения системы уравнений (13) определяется ток dI _{AB 1} :

A T - T _ T dIAB 1 = I2 B1 I1B1 .

А из третьего уравнения этой же системы уравнений определится ток dI _{CA 1} :

a T — T T dICA1 = I1C1 I2 C1 .

При известных токах dI _{AB 1} и dI _{CA 1} из первого уравнения системы уравнений (13) определится ток dI _{A 1} :

TT T T dIA1 = I1A1 dIAB 1 + dICA1 .

Теперь появилась возможность определить ряд укрупненных поперечных параметров:

д Т dI AB1 тт

U 2 A1 U 2 B1

т dICA1

Т _тт ;

U 2 C 1 U 2 A 1

Y a =

т dIA1

•                   .

U 2 A 1

Условия выполнения второго опыта от первого отличаются тем, что ключ S8 разомкнут, а ключ S7 замкнут. Вследствие этих переключений линейные провода А и С в конце анализируемой ЛЭП оказываются замкнутыми на «землю». В этом случае будут отсутствовать напряжения U2A2 и U2C2 , а также токи I2B2 , dIA2 , т           1т dIC2 и dICA2 :

U 2 A 2 = U 2 C 2 = 0 ;

т — ДТ — ДТ — ДТ - л

I 2 B 2 = dI A 2 = dI C 2 = dI CA 2 = 0 •

При таких условиях справедливы уравнения:

1 1 A 2 — dl AB 2 — 1 2 A 2 = 0;

1 1 b 2 — dl BC 2 + dl AB 2 — dl B 2 = 0.

Т          тг         Т

I 1 C 2 + ^dIBC 2 ^- I 2 C 2 = 0.

Из первого и третьего уравнений этой системы определятся токи dI _{AB 2} и dI _{BC 2} :

Т    —г т dIAB 2 = I1A 2 I2 A 2 ;

Т     — т dIBC 2 = I2 C 2  11C2 •

Из второго уравнения этой же системы уравнений определится ток dI _{B 2} :

тт т т dIB 2 = 11B 2 dIBC 2 + dIAB 2 •

Рассчитанные таким образом токи дают возможность определения еще двух укрупненных поперечных параметров:

т dIBC2

—^BC й _й ^;

^U 2 B 2 ^U 2 C 2

Y b =

т dIB2

т . U 2 B 2

Цель третьего опыта заключается в определении укрупненной полной проводимости Y _C . Для этого необходимо разомкнуть ключ S 9 и замкнуть ключ S 8. Состояние прочей коммутационной аппаратуры следует оставить без изменения. В результате этих действий линейные провода А и B окажутся замкнутыми на «землю»; напряжения U _{2 A 3} и U _{2 B 3} , а также токи I _{2 C 3} , dI _{A 3} , dI _{B 3} и dI _{AB 3} будут отсутствовать:

U 2 A 3 = U 2 B 3 = ⁰ ;

Т — ДТ — ДТ — ДТ — л

I 2 C 3 = ^dIA 3 = ^dIB 3 = ^dI AB 3 = ⁰ .

В таком случае будут справедливы уравнения:

T    i ДТ T — Л ■

1 1 A 3 ^{+ dI}CA 3 I 2 A 3 = ⁰ ;

Т                    Т

1 1 B 3 ^dIBC 3 I 2 B 3 = ⁰ ;

Т      дТ । дт       дТ — л

1 1 C 3 ^dICA 3 ^{+ dI}BC 3   ^dI 2 C 3 = 0.

Из первого и второго уравнения системы уравнений (14) определятся токи dI _{CA 3} и dI _{BC 3} :

Т — dICA 3 = I2 A 3 I1A 3 ;

Т — dIBC3 = 11B 3 I2 B 3 •

А из третьего уравнения этой же системы уравнений определится ток dI _{2 C 3} :

^dI 2 C 3 = I 1C 3 ^dICA 3 ^{+ dI}BC 3 •

Искомая укрупненная полная проводимость определится так:

Y C =

_т dI _{C 3} т ^. U 2 C 3

Таким образом, определены все указанные на схеме замещения анализируемой ЛЭП, изображенной на рисунке, укрупненные полные проводимости, иллюстрирующие укрупненные поперечные параметры исследуемой трехпроводной линии электропередачи.

Вещественные части укрупненных полных проводимостей определят укрупненные активные проводимости между линейными проводами, а также между проводами и «землей»:

G ab = Re ( Y ab ) ;

G BC = ^Re ( Y BC ) ^;

G ca = Re ( Y ca ) ;

Ga = Re ( Ya );

Gb = Re ( Yb );

Gc = Re ( Yc ) •

Мнимые части укрупненных полных проводимостей определят укрупненные емкостные проводимости между линейными проводами, а также между проводами и «землей». Поэтому величины соответствующих емкостей определятся следующим образом:

C = Im ( Y AB ) .

^AB     2 n f   ’

_ Im ( Y BC ).

C ^BC = 2 « f '

= Im ( Y CA )

‘     2n f

= Im ( Y A ) .

2 n f ’

= Im ( YA ) 2nf r _ Im(YC)

^CC =   2 « f

.

Так определяются численные значения укрупненных первичных параметров трехпроводной ЛЭП, содержащей в своем составе несколько однородных участков.

Результаты

Известны и широко применяются в инженерной практике множество методов определения режимных параметров ЛЭП. Но практически все они полагают, что анализируемый участок ЛЭП или вся линия электропередачи однородна либо представляет собой совокупность однородных участков. Естественно, это вносит существенную погрешность, поскольку любая реальная ЛЭП обладает неоднородностью в той или иной степени. Кроме того, в практических расчетах часто игнорируется неизбежное присутствие в ЛЭП линейной арматуры, что увеличивает погрешность вычислений. Избежать данной погрешности позволяет введение понятия «укрупненные параметры ЛЭП», которые определяются экспериментально по предложенной методике.

Правомочность и достоверность этого способа обеспечивается соответствующим техническим обеспечением. Это в первую очередь парк электроизмерительных приборов с соответствующими пределами и классами измерения. Поскольку расчетная часть предлагаемого метода не громоздка и не может являться причиной ощутимой погрешности, то получается, что погрешность этого способа определяется лишь классом точности используемых здесь электроизмерительных приборов и качеством используемых линий связи.

Заключение

Конкретизированные таким образом укрупненные параметры реальных ЛЭП создают возможность прогнозирования в первом приближении результатов передачи электрической энергии на частоте каждой гармонической составляющей. Такой прогноз может оказаться достаточным для оценки эффективности той или иной передачи электрической энергии.