Экспериментальное сравнение алгоритмов классификации символов в стенографических документах

Одним из этапов при распознавании рукописного текста является сегментация (выделение) строк. Для решения данной задачи предлагаются различные методы. При распознавании печатных текстов самым популярным является метод, связанный с построением проекции точек символов на ось, перпендикулярную строкам текста. Однако в случае рукописных документов при использовании данного метода возникают сложности, связанные с тем, что строки могут располагаться под некоторым углом, интервал между соседними строками может варьироваться и т. д. Поэтому при сегментации строк в рукописных документах используются либо его модификация, либо иные методы.

В работе [7] предлагается алгоритм, который динамически строит разделяющую линию между соседними строками. Для нахождения координат этой линии используется трехэтапный алгоритм. Первый этап алгоритма заключается в рекурсивном построении разделяющей линии между двумя строками с достаточно большим интервалом между ними. В качестве начальных точек разделяющих линий берутся локальные минимумы проекции точек символов на границу

изображения. Второй и третий этапы алгоритма заключаются в реализации обхода встречающихся на пути разделяющей линии символов. На втором этапе для этой цели используется огибание части встретившегося символа по контуру в случае, если огибаемая часть достаточно мала, если же этого сделать нельзя, тогда на третьем этапе алгоритма для нахождения точек разделяющей линии используется метод, суть которого заключается в следующем. Изображение с текстом делится на некоторое количество вертикальных прямоугольных секций. Внутри каждой секции строится проекция точек символов на границу этой секции, и локальные минимумы проекции являются точками, лежащими на разделяющей линии между двумя соседними строками.

Метод сегментации строк с разделением распознаваемого изображения на секции представлен в [5]. В данной работе дана модификация этого метода для того случая, если строки расположены под некоторым углом (необязательно одинаковым). Кроме того, при использовании рассматриваемого метода может возникнуть проблема, связанная с недостаточным количеством точек символов для какой-либо строки в секции, например, это может произойти, если секция попадает на разрыв между двумя соседними символами строки. Тогда проекция для данной секции не отобразит наличие существующей строки. Для решения этой проблемы в работе [10] предлагается для каждой секции использовать сглаживающую проекцию, которая зависит от количества точек символов в соседних секциях.

При использовании методов, связанных с построением проекций, предполагается, что между строками есть четко выраженные интервалы и количество пересечений строк достаточно мало. Однако в стенограммах, ввиду того что размеры символов сильно варьируются, есть надстрочные и подстрочные символы, каждая отдельная строка может иметь произвольную форму, четко выделить интервал между двумя соседними строками не всегда возможно, поэтому в случае стенографических документов использовать рассмотренные выше методы нецелесообразно.

В работах [8], [9] рассматриваются метод выделения строк с помощью группировки компонентов изображения, а также метод выделения строк с помощью размытия исходного изображения документа. Метод группировки заключается в том, что отдельные компоненты (наборы связанных пикселей) на изображении соединяются согласно их геометрическим и топологическим характеристикам. Общая стратегия метода состоит в сопоставлении каждой компоненте соответствующей точки в некотором пространстве характеристик (например, центр тяжести) и в расчете расстояний между точкой, соответствующей данной компоненте, и точками, соответствующими соседним компонентам. Две компоненты объединяются, если расстояние между соответствующими им точками не превышает заданного вручную либо, например, полученного путем обучения на заранее подготовленной коллекции документов [11]. Метод размытия заключается в том, что вначале к исходному изображению применяется эффект размытия (например, по Гауссу [6]), таким образом каждая строка преобразуется в сплошную закрашенную область, после чего для выделения отдельных строк применяются хорошо известные методы сегментации изображений.

Методы, связанные с размытием исходного изображения документа, также сильно зависят от интервалов между строками, так как если будет большое количество пересечений строк, то на размытом изображении будет весьма трудно выделить отдельные строки.

Среди публикаций на русском языке, описывающих проблемы сегментации строк, можно выделить монографию Л. А. Местецкого, в которой предложен метод распрямления строк на основе гранично-скелетного представления бинарного изображения сканированного документа [3]. Суть данного метода заключается в использовании гранично-скелетного представления бинарного изображения сканированного документа. Для распрямления используется внешний скелет изображения, под которым понимается скелет области, внешней границей которой является граница документа, а внутренними отверстиями - контуры изображенных в документе букв. По сути дела, речь идет о негативном изображении документа - белые буквы на черном фоне. Основная идея предлагаемого подхода заключается в том, что во внешнем скелете документа можно легко выделить ветви, лежащие между соседними текстовыми строками. Эти ветви можно использовать, чтобы аппроксимировать деформацию межстрочных пробелов на изображении. Затем по аппроксимации отдельных межстрочных пробелов можно построить аппроксимацию искажения всего документа. Данный метод может быть использован в том случае, если оригинальный текст содержал строго горизонтально ориентированные строки, то есть этот метод является некоторой корректировкой отсканированного документа, вследствие чего он также не может быть использован для выделения строк в рукописных документах, а тем более в стенограммах.

Наиболее применимыми методами для сегментации строк в стенографических документах являются методы группировки компонент, к которым относится предложенный нами алгоритм [1] распознавания строк методом построения графа связей. Его идея заключается в формировании списка связей, где для каждой связи заданы первая компонента, вторая компонента и расстояние между компонентами. Каждая компонента помещается в отдельную строку, и для каждой связи из списка выполняются следующие действия: 1) если компоненты, входящие в текущую связь, можно соединить, то есть для первой компоненты не задана следующая за ней компонента, а для второй компоненты не задана предшествующая, то объединяются строки, содержащие эти компоненты; 2) иначе, если компоненты соединить нельзя, то находятся вертикальные интервалы между компонентами строк, содержащими компоненты, входящие в связь, и если все интервалы не превышают заданный максимальный интервал, тогда объединяются строки; 3) выполняется переход к следующей связи. В отличие от других методов, на вход которых подается исходное изображение документа, для алгоритма распознавания строк методом построения графа связей входными данными является информация о месторасположении каждой отдельной компоненты, что облегчает задачу. Под компонентой в данном случае будет пониматься отдельный символ стенографического документа.

Кроме того, при распознавании стенографических документов возникает задача определения типа (основной, надстрочный и подстрочный) каждого символа в строке.

В работе [2] описаны предложенные нами алгоритмы классификации символов методами одинарной и двойной аппроксимации. Основная идея алгоритмов состоит в том, что строки в стенографических документах имеют форму, которую можно аппроксимировать полиномом некоторой степени. В данной статье рассматривается модификация этих алгоритмов, которая заключается в последовательном уменьшении ошибки аппроксимации за счет исключения части аппроксимируемых точек.

Кроме того, в статье приводятся результаты сравнения алгоритмов классификации без модификации и модифицированных алгоритмов классификации символов на основе заранее построенной контрольной выборки. При сравнении алгоритмов использовались такие оценки, как корректность (отношение числа правильно классифицированных символов к общему числу символов), точность, полнота, F-мера для каждого типа символов и обобщенная F-мера, которая представляет собой среднее значение оценок F-меры для каждого типа символов.

Сравнение алгоритмов проводилось в три этапа. Первый этап заключается в нахождении для каждого алгоритма оптимальных входных параметров (параметров, при которых достигается максимальное значение обобщенной F-меры) на каждом стенографическом документе из контрольной выборки и последующем сравнении оценок работы алгоритмов при найденных параметрах. Второй этап заключается в нахождении для каждого алгоритма входных параметров, при которых среднее значение оценок обобщенной F-меры на всех стенографических документах из контрольной выборки будет максимальным, и последующем сравнении средних значений обобщенной F-меры при найденных параметрах для каждого алгоритма. Третий этап заключается в определении скорости обучения каждого алгоритма на каждом стенографическом документе из контрольной выборки. Основными показателями скорости обучения алгоритмов классификации символов являются количество строк, на которых проведено обучения, контрольного стенографического документа и значение обобщенной F-меры, которое показал обученный алгоритм на данном документе.

Так как алгоритмы классификации символов определяют оценку вероятности, с которой каждый символ относится к тому или иному типу, было принято считать, что символ является основным, надстрочным или подстрочным, если вероятность данного события превышает 0,5. Кроме того, разбиение символов на строки выполнялось с помощью описанного выше алгоритма распознавания строк методом построения графа связей.

АЛГОРИТМЫ КЛАССИФИКАЦИИ СИМВОЛОВ МЕТОДАМИ ОДИНАРНОЙ И ДВОЙНОЙ АППРОКСИМАЦИИ

Алгоритмы детально рассмотрены в работе [2], поэтому приведем лишь краткое описание принципа их работы. После распознавания строки строится одна линия аппроксимации по центрам прямоугольников, описывающих символы строки, в случае алгоритма классификации символов методом одинарной аппроксимации, и две линии аппроксимации по центрам верхних и нижних сторон прямоугольников, в которые вписаны символы строки, в случае алгоритма классификации символов методом двойной аппроксимации. После чего в зависимости от расположения символов строки относительно построенной(ых) линии(ий) аппроксимации рассчитывается оценка вероятности принадлежности символа к тому или иному типу.

АЛГОРИТМЫ КЛАССИФИКАЦИИ СИМВОЛОВ МЕТОДАМИ ОДИНАРНОЙ И ДВОЙНОЙ

АППРОКСИМАЦИИ С УМЕНЬШЕНИЕМ ОШИБКИ

Модифицированные алгоритмы классификации символов отличаются от немодифицирован-ных только на этапе построения линии аппроксимации. Рассмотрим данный этап.

Вводятся два входных параметра алгоритма: error – максимальный процент, на который может уменьшиться ошибка аппроксимации, и exclusion – максимальный процент исключенных точек от общего числа аппроксимируемых точек.

Пусть P – множество аппроксимируемых точек.

^Р = { ( x i , У 1 ) , ( x 2 , У 2 ) ,-, ( x p , У р ) } .        ⁽¹⁾

Выполняются следующие действия:

• 1.    Строится полиномиальная аппроксимирующая функция ф _Р ( x ) по точкам из множества P ;

• 2.    Находится точка ( x j , y j ) , где

• 3.    Определяется множество Р' , которое получается из множества P исключением из него точки ( X j , У) ) ;

• 4.    Строится полиномиальная аппроксимирующая функция ф_Р■ ( x ) по точкам из множества Р' ;

• 5.    Определяется ошибка

j = arg max { y _t ^- ф р ( x ) } ;          (2)

i e 1...| P|

E i = X к -- ^- Ф р ( х )| ;            ⁽³⁾

• i e1...| Р |, i *. j

• 6.    Определяется ошибка

• 7.    Если выполняется неравенство ( E 1 - E ₂ ) / E 1 < <  error /100 и процент исключенных точек не превышает exclus on , тогда переходим на

E 2 = X l y ^- ф р ' ( x )l ;            ⁽⁴⁾

i e 1...| Р '|

второй шаг, при этом в качестве множества P будет выступать множество Р', а в качестве аппроксимирующей функции ф _Р ( x ) - функция фр ■ ( x ) .

Полученная в ходе выполнения вышеприведенных действий функция ф _Р ( x ) будет определять линию аппроксимации.

СРАВНЕНИЕ ЛУЧШИХ РЕЗУЛЬТАТОВ РАБОТЫ

АЛГОРИТМОВ КЛАССИФИКАЦИИ СИМВОЛОВ

Эксперимент проводился на четырех исторических стенографических документах, написанных А. Сниткиной под диктовку Ф. М. Достоевского. Эти документы были размечены вручную. Для каждого документа были найдены лучшие результаты работы каждого из четырех алгоритмов классификации символов, включающих алгоритм классификации символов методом одинарной аппроксимации, алгоритм классификации символов методом двойной аппроксимации, алгоритм классификации символов методом одинарной аппроксимации с уменьшением ошибки и алгоритм классификации символов методом двойной аппроксимации с уменьшением ошибки. Критерием, по которому выбирается лучший результат, является обобщенная F-мера.

В табл. 1 представлены оценки лучших результатов работы алгоритмов классификации символов для первой стенограммы, а также входные параметры, при которых достигаются эти результаты. К входным параметрам алгоритмов классификации символов относятся:

• •    m – степень аппроксимирующего полинома (используется в каждом алгоритме);

• •    λ – параметр, используемый при определении вероятности того, что символ является ос-

• новным либо неосновным (надстрочным или подстрочным), в алгоритме классификации символов методом одинарной аппроксимации и алгоритме классификации символов методом одинарной аппроксимации с уменьшением ошибки,

а также рассмотренные выше параметры ( error , exclusion ).

Как видно из представленных в табл. 1 оценок, лучший результат показал алгоритм классификации символов методом двойной аппроксимации с уменьшением ошибки.

СРАВНЕНИЕ МАКСИМАЛЬНЫХ СРЕДНИХ ЗНАЧЕНИЙ ОБОБЩЕННОЙ F-МЕРЫ ДЛЯ ВСЕХ ДОКУМЕНТОВ

Для каждого алгоритма классификации символов были найдены максимальные средние значения обобщенной F-меры на всех стенографических документах из контрольной выборки, а также входные параметры, при которых достигаются эти значения (табл. 2).

Алгоритм классификации символов методом двойной аппроксимации с уменьшением ошибки показал самые высокие средние значения обобщенной F-меры.

СРАВНЕНИЕ ОБЪЕМА ОБУЧАЮЩЕЙ ВЫБОРКИ ДЛЯ ОЦЕНКИ ТОЧНОСТИ АЛГОРИТМОВ КЛАССИФИКАЦИИ СИМВОЛОВ

Был проведен эксперимент по определению объема обучающей выборки (скорости обучения) алгоритмов классификации символов на каждом стенографическом документе. Оценка скорости обучения алгоритма заключалась

Таблица 1

Оценки лучших результатов работы алгоритмов классификации символов для первой стенограммы

Алгоритм	Методом одинарной аппроксимации			Методом двойной аппроксимации
Параметры	m = 4, λ = 0,0682			m = 3
Обобщенная F-мера	0,5087			0,5607
Корректность	0,724			0,8368
Тип символов	Осн.	Надстр.	Подстр.	Осн.	Надстр.	Подстр.
Полнота	0,7838	0,5333	0,4854	0,952	0,2667	0,4078
Точность	0,8651	0,1143	0,5495	0,8617	0,2	0,84
F-мера	0,8225	0,1882	0,5155	0,9046	0,2286	0,549
Алгоритм	Методом одинарной аппроксимации с уменьшением ошибки			Методом двойной аппроксимации с уменьшением ошибки
Параметры	m = 4, λ = 0,0386, exclusion = 50, error = 80			m = 1, exclusion = 30, error = 10
Обобщенная F-мера	0,5381			0,6244
Корректность	0,8056			0,8559
Тип символов	Осн.	Надстр.	Подстр.	Осн.	Надстр.	Подстр.
Полнота	0,9279	0,3333	0,3301	0,9432	0,3333	0,5437
Точность	0,8483	0,2778	0,5965	0,8871	0,3125	0,7671
F-мера	0,8863	0,303	0,425	0,9143	0,3226	0,6364

Таблица 2

Параметры				Обобщенная F-мера
m	λ	error	exclusion	Стенограмма	Среднее значение
				№ 1        № 2       № 3   1   № 4

Алгоритм классификации символов методом одинарной аппроксимации

				Максимальные значения F-меры
				0,5087	0,6744	0,5854	0,6945
4	0,0473			0,4696	0,5831	0,5661	0,6728	0,5729
4	0,0474			0,4696	0,5831	0,5661	0,6728	0,5729
4	0,047			0,4686	0,5831	0,5661	0,6728	0,57265
4	0,0471			0,4655	0,5831	0,5661	0,6728	0,571875
4	0,0472			0,4655	0,5831	0,5661	0,6728	0,571875

Алгоритм классификации символов методом двойной аппроксимации

				Максимальные значения F-меры
				0,5607	0,7172	0,6506	0,6756
2				0,5591	0,6886	0,5462	0,6756	0,617375
4				0,5524	0,6246	0,6287	0,6405	0,61155
1				0,5572	0,7172	0,4914	0,675	0,6102
5				0,5572	0,6	0,6506	0,6104	0,60455
3				0,5607	0,6558	0,5618	0,6344	0,603175

Лучшие средние значения обобщенной F-меры алгоритмов классификации символов

Алгоритм классификации символов методом одинарной аппроксимации с уменьшением ошибки

				Максимальные значения F-меры
				0,5381	0,6768	0,6254	0,6945
4	0,0481	15	15	0,5238	0,5921	0,5878	0,6561	0,58995
4	0,0479	15	15	0,5201	0,5921	0,5878	0,6561	0,589025
4	0,048	15	15	0,5201	0,5921	0,5878	0,6561	0,589025
4	0,0481	15	10	0,5237	0,5921	0,5887	0,6508	0,588825
4	0,0479	15	10	0,5199	0,5921	0,5887	0,6508	0,587875

Алгоритм классификации символов методом двойной аппроксимации с уменьшением ошибки

Максимальные значения F-меры 0,6244 0,7557 0,6612 0,7679 1 20 60 0,5855 0,7318 0,5274 0,7679 0,65315 1 20 65 0,5855 0,7318 0,5274 0,7679 0,65315 1 20 70 0,5855 0,7318 0,5274 0,7679 0,65315 1 20 75 0,5855 0,7318 0,5274 0,7679 0,65315 1 20 80 0,5855 0,7318 0,5274 0,7679 0,65315 в том, что на некотором количестве строк контрольного стенографического документа выполнялся поиск лучшего результата работы алгоритма, то есть результата, при котором достигается максимальное значение обобщенной F-меры. После чего при тех же входных параметрах, при которых был достигнут лучший результат на части строк, выполнялся запуск алгоритма на всем контрольном документе, при этом фиксировалось значение обобщенной F-меры. Таким образом, скорость обучения определяется количеством строк, используемых при обучении, и конечным значением обобщенной F-меры на всем стенографическом документе. На рисунке представлены графики зависимости значения обобщенной F-меры от количества обучающих строк для первой стенограммы.

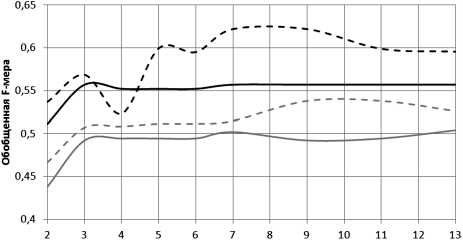
Количество обучающих строк

Алгоритм классификации символов:

---методом одинарной аппроксимации

---методом двойной аппроксимации

--методом одинарной аппроксимации с уменьшением ошибки

--методом двойной аппроксимации с уменьшением ошибки

Графики зависимости значения обобщенной F-меры от количества обучающих строк для первой стенограммы

Как видно из представленных графиков, лучший результат, начиная с пятой строки, показал алгоритм классификации символов методом двойной аппроксимации с уменьшением ошибки.

ЗАКЛЮЧЕНИЕ

Рассмотренные в статье алгоритмы будут реализованы в создаваемой компьютерной программе для распознавания исторических стенограмм [4].

* Работа выполнена при поддержке Программы стратегического развития ПетрГУ в рамках реализации комплекса мероприятий по развитию научно-исследовательской деятельности на 2012–2016 гг.

EXPERIMENTAL COMPARISON OF ALGORITHMS FOR SYMBOLS’ CLASSIFICATION IN SHORTHAND DOCUMENTS