Экспериментальные исследования аэродинамических характеристик модели корпуса несущей формы

Расширяющийся круг задач и требований, предъявляемых к летательным аппаратам (ЛА) в процессе развития авиации, определяет все многообразие видов ЛА, разнообразие их аэродинамических схем, компоновок, а также конфигураций, форм и взаимного положения основных агрегатов летательного аппарата, определяющих его внешний аэродинамический облик. Среди множества аэродинамических компоновок можно выделить класс самолётов, к основной несущей системе которых относится не только крыло, но и корпус самого летательного аппарата, обладающий определёнными несущими свойствами. Как правило, в таких случаях речь идёт об интегральных компоновках сверхзвуковых и гиперзвуковых самолётов, а также боевых самолётов истребительной или дальней стратегической авиации. В то же время придание несущей аэродинамической формы корпусу транспортного или пассажирского самолёта также имеет смысл, что позволит получить ряд преимуществ сравнительно с классическими компоновками транспортных самолётов. На малых и больших дозвуковых скоростях полёта несущей аэродинамической формой может вступать корпус самолёта со «сплюснутой» эллиптической формой в поперечном сечении. Подобное решение позволяет существенно повысить несущие свойства фюзеляжа и разгрузить крыло самолёта, что, в свою очередь, предоставляет возможность уменьшить площадь крыла и, как следствие, об-

легчает его конструкцию [1]. В этом случае можно получить более компактный самолёт с меньшими габаритами. Особый характер распределения воздушной нагрузки по размаху крыла при применении фюзеляжа подобной формы снижает величину изгибающего момента, действующего в силовых элементах конструкции крыла, что позволяет дополнительно уменьшить его массу [1]. В то же время, благодаря разгрузке крыла и особому характеру циркуляции по его размаху, становится возможным увеличение удлинения крыла с целью снижения индуктивного сопротивления самолёта.

Существует большое количество формул инженерной методики расчёта аэродинамических характеристик (АХ) круглых фюзеляжей [2] [3] [4], однако, аэродинамика некруглых корпусов большого удлинения остаётся недостаточно изученной. Хорошо развитые и часто применяемые в последнее время методы вычислительной аэродинамики [5] [6] [7] позволяют рассчитывать АХ ЛА самых любых форм, но, как и все математические модели, требуют их верификации и настройки на основе данных экспериментальных исследований.

Цель работы: определение основных интегральных аэродинамических характеристик модели фюзеляжа некруглой формы экспериментальным методом – путём продувки модели в аэродинамической трубе.

МЕТОДИКА ИССЛЕДОВАНИЯ. ЭКСПЕРИМЕНТАЛЬНАЯ УСТАНОВКА.

МОДЕЛЬ

Экспериментальные исследования основных интегральных АХ модели фюзеляжа некруглой формы проведено путём продувки модели в аэродинамической трубе весовым методом.

Экспериментальная установка представляет собой испытательный комплекс, состоящий из аэродинамической трубы АДТ Т – 3 СГАУ (рис. 1) и информационно – измерительной системы (ИИС), представляющей собой многоканальную измерительную структуру, основа которой является плата сбора информации L-1250.

Аэродинамическая труба Т – 3 СГАУ [8] замкнутого типа, оснащена открытой рабочей частью (длина L = 1000 мм) с прямоугольным соплом размерами B = 600 мм (ширина), Н = 400 мм (высота). Труба Т – 3 постоянного действия, предназначена для проведения эксперимента на малых дозвуковых скоростях (до V = 60 м/с). Степень поджатия потока в трубе составляет 6.

Поток в рабочей части трубы создаётся центробежным вентилятором, ротор которого представляет собой крыльчатку. Вентилятор приводится в движение электродвигателем постоянного тока. Мощность двигателя 45 кВт. Скорость потока может изменяться за счет изменения числа оборотов электродвигателя установки. Максимальное достижимое число Рейнольдса, рассчитанное по максимальной скорости потока и эквивалентному диаметру выходного сечения сопла (0,553 м) достигает Re = 182000,5.

Рабочая часть трубы оборудована механизмом « α-β » перемещения модели и координатным стендом «X, Y, Z» для перемещения насадка. Положение модели в рабочей части определяется в земной системе координат OXYZ. Ось OX направлена по потоку, OY- вверх, ось OZ- в горизонтальной плоскости, образуя левую систему координат. Модель устанавливается на аэродинамических тензовесах. Диапазон перемещения модели по углу атаки -10⁰ ≤ α ≤ +20⁰, по углу скольжения -20⁰ ≤ β ≤ +20⁰. Тензовесы представляют собой устройство, содержащее тензорезисторные преобразователи неэлектрических величин (упругие деформации) в электрический сигнал. Выходные напряжения подаются на усилители тензовесов с коэффициентом усиления. Далее усиленный сигнал поступает на плату сбора информации. Весы позволяют измерять нагрузки по шести компонентам X, Y, Z, M_x, M_y, M_z в системе координат, связанной с моделью [8].

Объектом исследования является модель несущего фюзеляжа, основные геометрические характеристик приведены в таблице 1, а на рисунках 4 (а, б), 5 (а, б) представлены основные проекции общего вида модели фюзеляжа, а также конструкция модели (рис. 3).

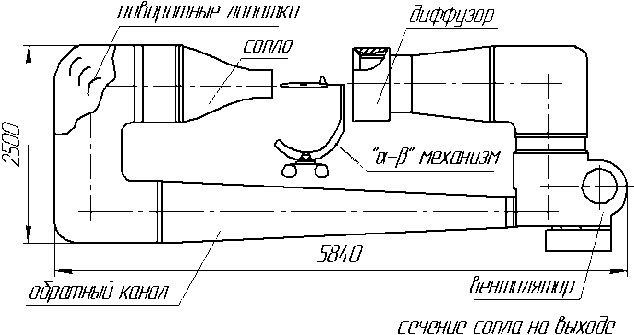
Рис. 1. Схема аэродинамической трубы Т-3 СГАУ (размеры в мм)

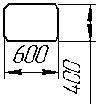
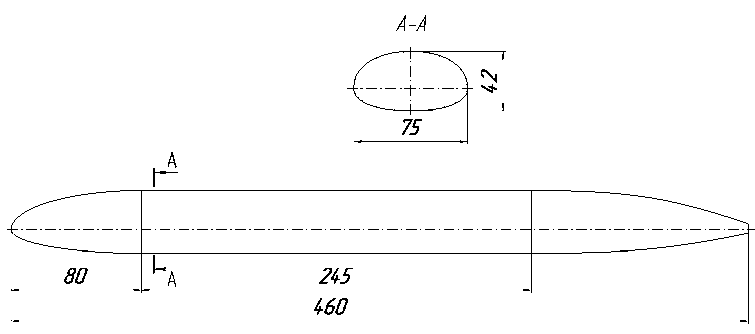
Рис. 2. Геометрические характеристики исследуемой модели, мм

Таблица 1. Основные геометрические характеристик аэродинамической продувочной модели

l, м	^ м , мм2	F , м2	\	\ . ч	\ . .	a	h	f
0,46	2604	0,0778	8	2,4	1,4	0,6	0,56	2 - 1

Державка весов

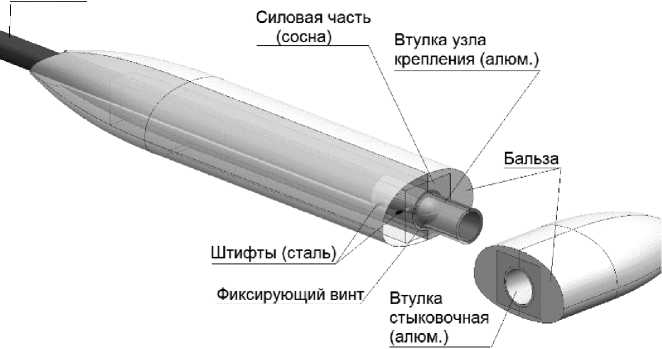
Рис. 4 а, б. Общий вид продувочной модели

Рис. 3. Конструкция аэродинамической продувочной модели

Рассматриваемая модель корпуса условно разделена на три части: носовую, цилиндрическую и кормовую. Эквивалентный диаметр миделя корпуса d м э = 57,6 мм. Площадь миделя корпуса S_M = 2604 мм². Удлинение корпуса Л к = 8 , длина l = 0,46 м. Удлинения носовой и кормовой частей фюзеляжа Л н ч = 1,4 и Л к ч = 2,4 . Площадь омываемой поверхности F = 0,0778 м².Попереч-ное сечение корпуса некруглой формы, состоит из 4 дуг эллипса с разным соотношением полуосей. Отношение малых полуосей нижнего и верхнего эллипсов равно а = 0,6 , а отношение высоты к ширине поперечного сечения (отношение суммы малых полуосей к большой оси) равно h = 0,56 . Теоретические обводы модели образованы поверхностями второго порядка конического сечения, натянутой по направлению строительной горизонтали фюзеляжа с постоянным по длине значением дискриминанта f = V2 - 1 .

Модель изготовлена автором работы из дерева: внутренняя силовая часть модели выполнена из сосны, формообразующая часть – из бальзы.

Внутри модели установлен узел крепления в виде втулки, предназначенной для установки модели на державку тензовесов в АДТ. Кроме этого, предусмотрено продольное отверстие внутри модели диаметром 23 мм для установки её на державку тензовесов. Втулка изготовлена из алюминиевого сплава с помощью токарной обработки. Модель конструктивно выполнена разборной для удобства установки её на державку весов; состоит из двух частей: основной и носовой, которые стыкуются между собой с помощью втулки, используемой для крепления модели на весах. Силовая часть фюзеляжа склеена из двух половинок по плоскости симметрии. На силовую часть наклеен бальзовый шпон с припуском, который после лезвийной, затем абразивной обработки образовывает теоретические обводы модели. Осуществлён контроль аэродинамической поверхности с помощью контрольных шаблонов. На поверхность затем нанесён грунт и краска. Втулка крепёжного узла вклеена и про-штифтована четырьмя штифтами из стали. После предварительных продувок было принято реше-

Рис. 5. Общий вид модели а) с расстыкованной носовой частью; б) снятый обтекатель с отверстия в хвостовой части модели, предназначенного для установки модели на державку тензовесов

ние оснастить модель вертикальным оперением (киль площадью S = 3250 мм2, стреловидностью по передней кромке χ = 420, удлинением λ = 1,6) с целью предотвращения колебаний в путевом канале. Положение центра тяжести модели фюзеляжа относительно его носка х = 0 194 м или ц.т      , хц т = 0,42 в долях длины модели.

Исследования АХ рассматриваемой модели проводятся при скорости потока 30 м/с в широком диапазоне углов атаки -5 o <  a <  +12^o, соответствующем диапазону полётных и взлётно-посадочных углов атаки, и в диапазоне углов скольжения -12^o <  a <  +12^o. Информационноизмерительная система экспериментальной установки выдает в процессе эксперимента значения интегральных характеристик, а именно: продольной, нормальной и боковой силы, а также значение продольного момента и момента рыскания при различных углах атаки.

Во всем диапазоне углов атаки измерялся скоростной напор в воздушном канале. Температура окружающей среды во время проведения эксперимента составляла t = 23^o C, атмосферное давление Р = 745 мм. рт. ст. Число Рейнольдса, рассчитанное по длине корпуса, при этом составило Re = 9 ^. 10⁵.

РЕЗУЛЬТАТЫ ИССЛЕДОВАНИЙ

Результаты экспериментальных исследований представляются в виде зависимостей коэффициентов подъёмной силы от угла атаки cya (a) (рис. 6 а), коэффициента сопротивления от угла атаки cха (а) (рис. 6 б), коэффициента продольного момента от угла атаки и коэффициента подъёмной силы mz(α) , mz(суа) (рис. 7 б, 8 а), коэффициента боковой силы от угла скольжения cza (в) (рис. 9 б), полярой первого рода суа (сха ) (рис. 7 а). Моментные характеристики модели представлены относительно центра тяжести модели. Ниже представленные аэродинамические зависимости являются математическими ожи- даниями аэродинамических коэффициентов при различных углах атаки, полученные в результате статической обработки экспериментальных данных. Среднеквадратичное отклонение по коэффициенту подъёмной силы в среднем составило ст = 0,0109, коэффициент вариации в среднем V = 3,14 %; по коэффициенту сопротивления ст = 0,0118, V = 5,4 %; по коэффициенту продольного момента ст = 0,0032, V = 2 %.

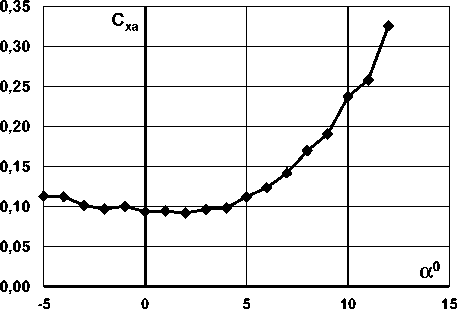
Анализ этих зависимостей позволяет утверждать, что зависимость подъёмной силы от угла атаки имеет нелинейных характер, что также характерно и для круглых изолированных фюзеляжей. В диапазоне полётных углов атаки 0 0 <  a <  4^o зависимость c ya ( а ) близка к линейной. На угле атаки а = 0 коэффициент подъёмной силы равен с_ya = 0,042 , что объясняется несимметричной формой поперечного сечения фюзе л яжа относительно горизонтальной плоскости ( а Ф 1). В связи с этим угол атаки нулевой подъёмной силы равен а ₀ «- 1,2 0 (рис. 6 а). Зависимость коэффициента сопротивления от угла атаки позволяет утверждать, что минимальный коэффициент сопротивления равен c_хa mi n = 0,091 и достигается на угле атаки а « 1 0 ..2⁰ при c ya = 0,07...0,1 , что также очевидно на поляре первого рода (рис. 6 б, 7 а). Производная коэффициента подъёмной силы по углу атаки (при c ya ^ 0 ) c ^ , = 0,035 1/градус, что является хорошим показателем: подобные значения несущих свойств круглых корпусов ( c ^ a ) достигается только у изолированных носовых частей круглых корпусов [3] [2]. Критического угла атаки и резкого падения подъёмной силы по его достижению в рассмотренном диапазоне углов атаки не наблюдается (рис. 6 a, 7 а): с увеличением угла атаки производная коэффициента подъёмной силы по углу атаки только возрастает c ^ a Т . Такой характер протекания зависимостей c ya ( а ) и c_ya ( c_ха ) характерен для бескрылых летательных аппаратов и крыльев малого удлинения [3] [4]. Зависимость коэффи-

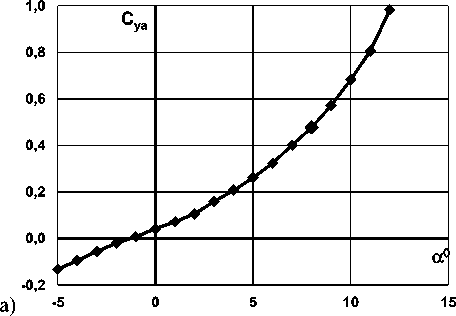
Рис. 6. Зависимости коэффициентов а) подъёмной силы; б) силы сопротивления от угла атаки

циента продольного момента от коэффициента подъёмной силы mzcуа позволяет сделать вывод о статической неустойчивости рассматриваемой д mz модели, поскольку производная    z положи-

0С уа тельна почти во всем диапазоне исследованных д mz углов атаки. Значение производной    z опре- дс уа деляет положение фокуса по углу атаки относительно моментной точки (в данном случае центр . - а    д m тяжести) х, =--= — 0,925 , что находится f     дсуа на 0,425 м впереди центра тяжести или 0,3 м впереди носка модели корпуса. Статическая неустойчивость объясняется наличием сужающейся комовой части на модели, что обуславливает положение фокуса по углу атаки впереди носка корпуса [2]. Степень статической неустойчивости х -xaf = 0 + 0,925 = 0,925 или 92,5 %.

ц . т      f

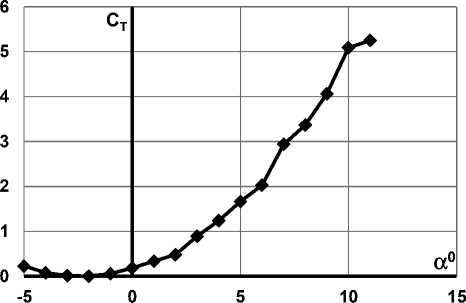
Нелинейный характер зависимости mzcya (рис. 7 б) (как и cya(α) объясняется схождением вихрей с боковых кромок корпуса даже на небольших углах атаки (а> 4o..5o) и возможными срывами на кормовой части, которые меняют знак произво-c дной mzy после а > 9..100. Причем, чем больше удлинение корпуса, тем большую нелинейность получают зависимости mzc a и c a(α) [3]. Несмот-yy     c ря на изменение значения производной mzya после а > 9..100, зависимость производная сО продолжает расти (рис. 8 a), что вероятнее всего происходит из-за роста разряжения над носовой частью и увеличением коэффициента подсасывающей силы cT с увеличением угла атаки (рис. 8 б). Коэффициент подсасывающей силы вычислен из выражения коэффициента отвала поляры 1c

A = —---2-, который был найден из формулы cya cya сха = сх0 + АСУа [4]. сх0, а также сха и суа для каждого угла атаки известны из эксперимента.

Значение производной коэффициента продольного момента по углу атаки в линейном диапазоне углов атаки т ^ = 0,0275 1/градус. Коэффициент продольного момента при нулевой подъёмной силе m z ₀ = — 0,0265 , поскольку а

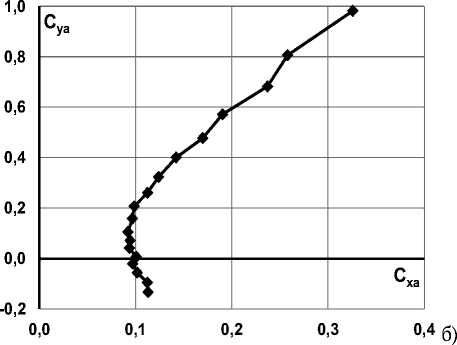
Рис. 7. Зависимости а) поляра первого рода;

б) коэффициента продольного момента от коэффициента подъёмной силы

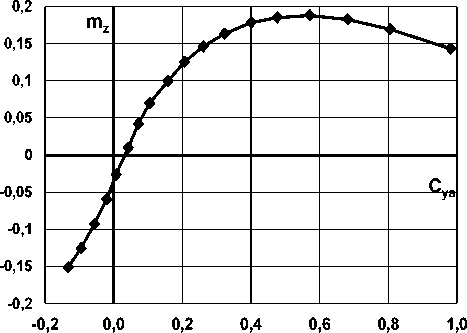
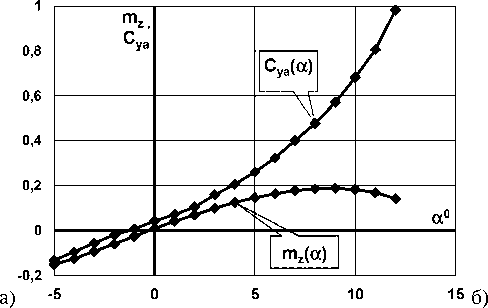
Рис. 8. Зависимости коэффициентов а) подъёмной силы и продольного момента; б) подсасывающей силы от угла атаки

• < 1. Максимальное аэродинамическое качество модели корпуса К_max = 3,12 достигается на углах атаки а = 9^о..11^о(рис. 9 a).

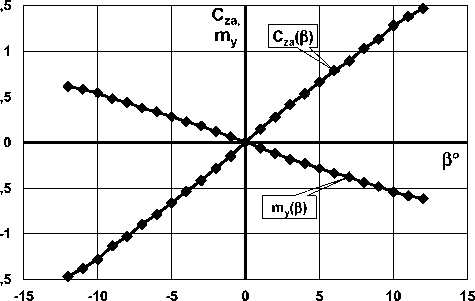
Зависимость коэффициентов боковой силы и момента рыскания от угла скольжения c za ( в ) и m y ( в ) имеют линейный характер практически во всем диапазоне рассмотренных углов сколь-жения-12 o <  в <  12 o (рис. 9 б), что объясняется наличием вертикального оперения, а в ₀ = 0 и m y 0 = 0 , т.к. модель симметрична. Очевидно, что модель устойчива в канале рыскания, т.к. т_у ^в < 0. Фокус по углу скольжения модели рас-

• -в   5 m

положен на расстоянии х в =--- = 0,396 или

• ¹      5 C za

х ^ = 0,182 м позади центра тяжести. Таким образом, запас статической устойчивости в канале рыскания 39,6 %. Несмотря на то, что сужающаяся кормовая часть корпуса обуславливает положение фокуса впереди его носка, введённое вертикальное оперение обеспечивает большой запас статической устойчивости в канале рыскания, переместив фокус по углу скольжения далеко за центр тяжести.

ВЫВОДЫ

Анализ полученных результатом позволяет сделать следующие выводы:

• –    рассматриваемая модель несущего корпуса обладает хорошими несущими свойствами с ^ = 0,035 1/градус (при с ya ^ 0 );

• –    модель обладает высоким аэродинамическим качеством К_max = 3,12, которое достигается на углах атаки а = 9^o..11 o ;

• – зависимость коэффициента подъёмной силы от угла атаки является нелинейной;

  – в исследованном диапазоне углов атаки -5^o <  а <  +12⁰ не наблюдается падения подъёмной силы, связанным с достижением критического угла атаки, наоборот, производная коэффициента подъёмной силы по углу атаки С “ _а возрастает с увеличением угла атаки (при а <  +12⁰);

  – несимметричная форма поперечного сечения корпуса обуславливает значение угла атаки нулевой подъёмной силы, отличное от ноля О ,«- 1,2 0 ;

  – модель статически неустойчива в продольном канале х ц т - х “ = 92,5% , и имеет большой

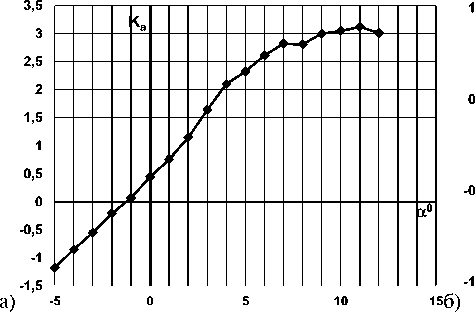
Рис. 9. Зависимости а) аэродинамического качества от угла атаки; б) коэффициента боковой силы и момента рыскания от угла скольжения

запас статической устойчивости в канале рыскания х т - х ^в = - 39,6% ;

– зависимости коэффициентов боковой силы от угла скольжения c za ( в ) и момента рыскания от угла скольжения m y ( в ) линейные в рассмотренном диапазоне-12^о <  в <  +12^о;

– производная коэффициента продольного момента по углу атаки m “ = +0,0275 в линейном диапазоне m z ( а ) и производная коэффициента момента рыскания по углу скольжения т ^ = -0,048;

– на носовой части модели реализуется подсасывающая сила, которая растёт с увеличением угла атаки.

Таким образом, можно утверждать, что придание корпусу некруглой в поперечном сечении формы позволяет получить высокие несущие свойства с ^а _а = 0,035 1/градус, хорошее аэродинамическое качество К_max = 3,12 и снизить степень статической неустойчивости (сравнительно с корпусами круглого сечения). Однако такие характеристики присущи изолированным несущим корпусам, поэтому исследования АХ таких корпусов следует проводить в компоновке с крылом с целью определения их взаимного их влияния на АХ летательного аппарата.