Экспериментальные исследования деформаций бетона при разгрузке на нисходящем участке и повторном нагружении

Представленные в статье результаты являются продолжением исследований, опубликованных ранее [1]. В указанной статье исследовались закономерности формирования диаграмм «напряжение – деформация» бетона под влиянием переменных режимов нагружения и деформирования. Эти режимы возникают при сопротивлении бетона в статически неопределимых системах под действием режима внешнего нагружения. На диаграммах появляются два характерных участка: первый, восходящий, характеризуемый ростом напряжения и деформации; второй, нисходящий, характеризуемый увеличением деформации и уменьшением напряжения. Характерными точками на диаграмме являются максимальное напряжение – соответствующая деформация и минимальное напряжение – соответствующая деформация. Изучены особенности образования и накопления повреждений (микротрещин) внутри бетона, на основе которых предложен критерий разрушения структуры бетона и определения величины предельной деформации.

Введена характеристика статически неопределимой системы в «точке», в которой анализируется сопротивление бетона и формирование диаграммы «напряжение – деформация».

Эта характеристика названа «жесткостью» системы в точке по определенному направлению. Установлено, что в зависимости от величины «жесткости» системы изменяется величина предель- ной деформации, определяющей момент прекращения бетоном сопротивляться нагружению (разрушение). Выяснилось, что этот момент может находиться на нисходящем участке и смещаться в зависимости от «жесткости» системы в точке.

Появление нисходящего участка на диаграммах «напряжение – деформация» исследователи наблюдали давно [2–5]. Внимание обращалось на факт появления нисходящего участка и определения его параметров. Результаты исследований использовались в расчетах [6]. Исследования разгрузки с нисходящего участка диаграммы и повторного нагружения в научной литературе авторами не обнаружено. Исследователи много занимались разгрузкой и повторными нагружениями бетона на восходящем участке диаграммы в связи с решением задач динамического сопротивления [7–10] и выносливости [11, 12]. Необходимость изучения сопротивления бетона при разгрузке с нисходящего участка и повторного нагружения обусловлена тем, что конструкции в процессе эксплуатации могут подвергаться воздействию опасных природных явлений и техногенных воздействий. Это может быть размыв грунтового основания в результате аварий на водоводах, подтопление территорий природными водами; разрушение части элементов конструкций зданий и сооружений от воздействия взрывов, ударов, а также местной (локальной) нагрузки вследствие нарушения правил эксплуатации, дефектов материалов и от- дельных конструкций. В связи с этим возникла необходимость в изучении повреждений [13–16], принятии мер безопасности и расчетного обоснования [17–25]. Имеются работы, в которых обосновывается возможность допускать развитие остаточных деформаций локальных разрушений (повреждений) при расчетах конструкций на воздействия аварийного типа [26]. Следует выяснить эти особенности.

При локальных повреждениях строительных конструктивных систем, когда зона повреждений не превышает критический размер [19], система в целом способна сопротивляться внешним воздействиям. В этих случаях в системе возникает «зона разгрузки». Особенность этой зоны состоит в том, что бетон может находиться в состоянии деформирования на нисходящем участке диаграммы и разгружаться после разрушения рядом расположенной зоны локального повреждения. Поскольку система в целом сохраняет способность сопротивляться внешним воздействиям, то экономически целесообразно восстановление поврежденных элементов и продолжение эксплуатации. Это вызывает повторное нагружение элементов в «зоне разгрузки». В связи с этим возникает задача расчета этой зоны и его экспериментального обоснования.

Учитывая вышеизложенное, можно считать, что знания о разгрузке и повторном нагружении бетона в «зонах разгрузки» будут необходимы для оценки состояния этих зон и возможности их последующего повторного нагружения. Это определяет актуальность исследований, приведенных ниже, и получения ответов на следующие вопросы:

• 1)    может ли бетон сопротивляться после разгрузки с нисходящего участка и повторного нагружения;

• 2)    как формируются диаграммы разгрузки и повторного нагружения.

Логично предположить следующее: если бетон разгрузить до появления предельной деформации на нисходящем участке, то он будет обладать некоторым сопротивлением, а для выполнения расчетов в этом случае необходима информация о форме диаграмм разгрузки и повторного нагружения.

Методика исследований

Подробно методика исследований для получения диаграмм с нисходящим участком приведена в статье [1]. Ее особенность состоит в том, что нагружение бетона производилось в специальном устройстве (кондуктор) [27], которое является один раз статически неопределимой системой с возможностью регулирования ее «жесткости» Вк. Введена характеристика лт = Вк/В0 (коэффициент стеснения), где В0 - жесткость бетонного образца. В зависимости от значений Вк и пг появлялся нисходящий участок зависимости «напряжение – деформация» бетона и менялись его параметры. Характерными точками диаграммы приняты: omax (максимальное напряжение), соответствующая деформация - eR и omin (минимальное напряжение на конце нисходящего участка), соответствующая деформация - Eb,max• На нисходящем участке установлена точка, соответствующая предельной деформации бетона - sbult по характеру изменения внутренних структурных повреждений.

В приведенных исследованиях реализованы следующие программы испытаний образцов бетона 100 х 100 х 400 мм:

• А)    при коэффициенте п_г = 0,408 производилась разгрузка с нисходящего участка и их последующее нагружение без кондуктора (п_г = 0) до разрушения;

Б) нагружение в кондукторе, разгрузка с нисходящего участка и повторное однократное нагружение в кондукторе до разрушения;

• В)    нагружение в кондукторе, разгрузка с нисходящего участка и последующее не многократное нагружение в кондукторе до разрушения.

Результаты испытаний

Программа «А». Образцы в виде бетонных призм - 100 х 100 х 400 мм, изготовленных из состава соответственно (Ц:П:Щ:В/Ц) – 1:2,1:5,2:0,52. Нагружение без кондуктора (п_г = 0) показало: прочность 16,6 МПа, модуль упругости – 2,5 МПа, длительность ступени нагружения – 10 мин, максимальная деформация - 225 - 10^-5. Нагружение в кондукторе (п_г = 0,408) и последующая разгрузка после достижения деформации (225, 265, 298, 320, 337, 350, 412, 475 и 592 - 10^-5) показало следующее. Максимальное напряжение при п_г = 0,408 увеличилось в 1,15 раза по сравнению с п_г = 0. Повторное нагружение показало уменьшение прочности бетона пропорционально уменьшению напряжений на нисходящем участке (табл. 1). Коэффициент пропорциональности изменялся в пределах – 0,8 (при максимальном напряже-

Таблица 1

Сопоставление прочности при повторном нагружении с напряжениями на нисходящем участке

^b Деформация бетона на нисходящем участке диаграммы sb, 10 5 225 265 298 320 337 350 412 475 592 Величина напряжения, МПа 18,8 18,0 17,6 17,2 16,6 16,5 14,0 11,2 8,6 Прочность при повторном нагружении, МПа 15,0 14,1 11,2 10,1 10,3 9,6 9,38 6,4 5,2 нии), 0,6 (при минимальном напряжении в конце нисходящего участка).

В сравнении с прочностью бетона при п_г = 0 (нисходящий участок отсутствует) снижение прочности пропорционально коэффициенту в пределах 0,92-0,69.

Программа «Б». Нагружение в кондукторе при п_г = 0,33 и п_г = 0,93 - 0,96 образцов состава -1:2,1:5,2:0,53 (прочность - 16,5 МПа, модуль упругости - 2,4 МПа), разгрузка с нисходящего участка и повторное нагружение в кондукторе до разрушения. Результаты показаны на рис. 1. Следует отметить следующее. Повторное нагружение в кондукторе приводит к появлению «повторного (нового)» нисходящего участка, параметры которого зависели от величины п_г в большей мере, чем при однократном «первичном» нагружении: при п_г = 0,33 повторный нисходящий участок располагался ниже первичного (рис. 1б), а при п_г = 0,93-0,96 -ниже первичного. На рис. 1в показано сопоставление диаграмм I*, II* - соответственно при однократном нагружении при п_г = 0,93 и 0,33, а I, II -повторное однократное нагружение соответственно при п_г = 0,93 и 0,33; III - повторное нагружение без кондуктора (п_г = 0).

Программа «В». Состав бетона предыдущий, а нагружение в кондукторе при п_г = 0,93-0,96.

Затем разгрузка и немногократное повторное нагружение (рис. 2). Видно, что диаграмма повторного нагружения в кондукторе зависит от номера цикла (рис. 2б). Следует отметить понижение максимального напряжения с увеличением номера цикла и формы диаграммы.

Особенности формирования диаграмм разгрузки с нисходящего участка и повторного нагружения установлены путем применения двух факторов. Первый - нагружение, осуществлялось ступенями с выдержками во времени. Ступени нагружения создавались быстро (около - 10 с), чтобы считать их условно-мгновенными, а соответствующие деформации - упругими. Фиксировались продольные и поперечные деформации, что давало возможность вычислять изменение коэффициента поперечной деформации. Второй - фиксировалось время прохождения ультразвука, что позволяло судить об изменениях в структуре бетона.

Установлены следующие особенности формирования диаграмм разгрузки бетона в кондукторе. При условно -мгновенном уменьшении ступени нагрузки уменьшается напряжение и продольная деформация. За время выдержки напряжение увеличивается, а продольная деформация продолжает уменьшаться. Эти явления позволяют предположить, что диаграмма формируется за

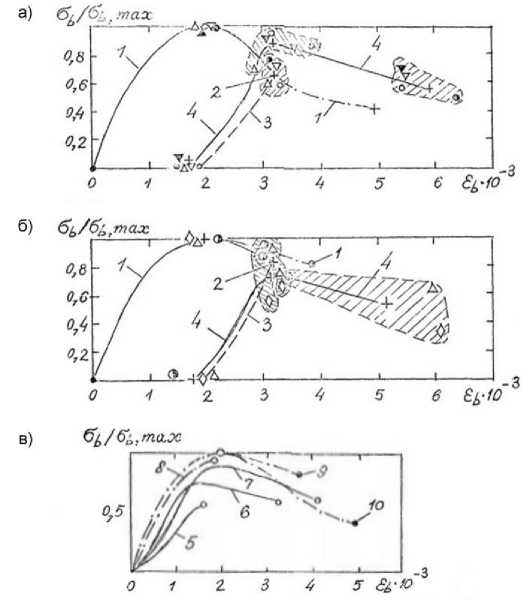
Рис. 1. Диаграммы одноосносжатого бетона при однократном и повторном нагружениях; а) при пг = 0,96; б) пг = 0,33; в) сопоставление диаграмм: 1 – однократное нагружение до разрушения; 2 – точка начала разгрузки; 3 – диаграмма при разгрузке; 4 – диаграмма при повторном однократном нагружении; 5, 6 и 7 – повторное нагружение до разрушения соответственно при пг = 0; 0,33 и 0,96; 8, 9, 10 - первичное нагружение до разрушения при пг = 0; 0,33 и 0,96 соответственно

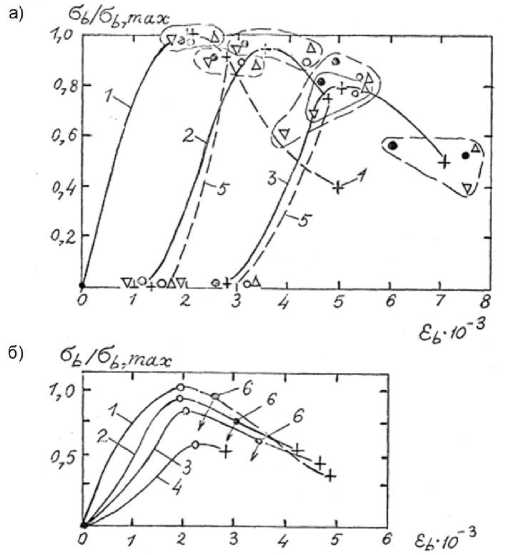
Рис. 2. Малоцикловое нагружение одноосносжатого бетона ( п _г = 0;93-0,96): а) диаграммы при нагружении и разгрузке; б) сопоставление диаграмм при нагружении 1, 2, 3, 4 – соответственно первое, второе, третье и четвертое нагружения; 5 - диаграммы разгрузки; 6 - точки начала разгрузки

счет двух процессов: процесса релаксации и восстановления напряжений, обусловленных проявлением «прямой и обратной» быстро натекающей ползучести [28]. Под действием этих процессов диаграмма искривляется в сторону оси деформаций как при разгрузке, так и при повторных нагружениях.

При разгрузке с различных точек нисходящего участка в бетоне наблюдается увеличение коэффициента поперечной деформации и одновременное увеличение времени прохождения ультразвука. Это свидетельствует об увеличении накопления внутренних повреждений в его структуре.

При повторных нагружениях бетона в кондукторе после разгрузки с нисходящего участка отмечались изменения формы диаграмм, аналогичные тем, которые обычно наблюдаются при испытании бетона на многократное повторное нагружение.

Если разгрузка осуществлялась с начала нисходящего участка (около максимального напряжения), то диаграмма повторного нагружения имела выпуклость в сторону оси напряжений. По мере отдаления точки разгрузки к концу нисходящего участка на диаграмме повторного нагружения появлялась кривизна двух противоположных знаков и точка перегиба. Начальный модуль деформации при повторном нагружении существенно снижался по мере отдаления от максимального напряжения (к концу нисходящего участка). А также наблюдалось снижение коэффициента поперечной деформации и увеличение времени прохождения ультразвука.

Параметры диаграмм разгрузки и повторного нагружения

Использовались результаты экспериментальных исследований Ю.А. Ивашенко, А.Д. Лобанова (81 образец) однократного и повторного нагружения, а также результаты экспериментальных исследований [29-32].

При определении параметров введены следующие обозначения:

• 1)    ^ тах и о ^ах — максимальное напряжение соответственно при первом и повторном нагружениях (соответствующие деформации - e_R и г / );

• 2)    а_и и a U - минимальное напряжение, соответствующее величине предельной деформации - ^ги ^{и г}и ,

• 3)    ^£ьаск - деформация, определяющая точку на нисходящем участке, с которой начинается разгрузка;

• 4)    г₀ - остаточная деформация после разгрузки ( а = 0) при первом нагружении;

• 5)    e _r - остаточная деформация в момент начала повторного нагружения (изменение г₀ -e_R = Е_ер ).

Ниже приведены эмпирические формулы для вычисления параметров:

• а) упругое последействие

• ^гер   ^р ( ^гR    O" max /^ b X                        ⁽¹⁾

где Е_ь - начальный модуль упругости бетона при первичном нагружении; Р – коэффициент, учитывающий долю восстанавливающейся деформации:

Р = 0,05 + 0,1 (£ „ - е_Ьаск )/(£_м - £ r ) ;     (2)

• б)    остаточная деформация

£ r = (0,94 СОьаск - 0,27)£_м , ^где ^ Ьаск    ^£Ьаск ^{/ £}и ;

• в)    деформация начального уплотнения при повторном нагружении (величина от начала повторного нагружения до точки изменения кривизны диаграммы):

£ 10 = £ / = (6,67^ ьаск - 2,17)£_е р ;          (3)

• г)    максимальное напряжение при повторном нагружении

а /   - К/   ■ о/ umax   ±vmax  5max ,

где K m _ax - коэффициент по табл. 2; ^ max — максимальное напряжение при повторных нагружениях по ГОСТ 24452-80 длительностью TR (указания в п. 3.9);

• д)    деформация, соответствующая напряжению 5 max

£ R = ^£ r ,                                       (5)

где £/ - деформация, соответствующая 5max по методике ГОСТ 24452-80 п. 3.9;

• е)    предельная деформация при повторном нагружении

£U = zU • eR, где zU — коэффициент по табл. 2;

• ж)    напряжение, соответствующее предельной деформации при повторном нагружении

5u = Ли 5max , где ^U — коэффициент по табл. 2.

• з)    при выполнении условия

• eR — еЬаск < eu.

Значения 5/_аск и £ / вычисляются по формулам

5max =(1,30 - 0,98 Шьаск )5max ,(9)

eR = (0,60/^ьаск - 0,05)8r.(10)

Ниже приведена табл. 2, в которой значения коэффициентов из опытов определяются в зависимости от изменения скоростей деформирования бетона (режим деформирования). При ступенчатом нагружении скорость деформирования зависит от времени действия ступени нагрузки:

• U_£ = Ae/At или более точно

U e =lim At_0 ^E(ti+At)"^E(ti)  ,                   (11)

Таблица 2

Значения коэффициентов к '„_ах , ^ U , z U

Изменение скорости деформирования при различном режиме нагружения		Опытные значения коэффициентов при различных величинах шЬаск
U (t R ) U (t 0 )	U T (tn) U (t 0 )	0,4	0,5	0,6	0,7	0,8	0,9	1
≥ 4,30	∞
3,05	5,25	1,05
		0,74/2,22
2,52	4,08	1,07	1,09
		0,63/2,31	0,79/2,17
1,88	2,70	1,08	1,12	1,16
			0,67/2,30	0,80/2,15
1,52	2,00		1,16	1,24	1,27
				0,69/2,27	0,81/2,13
1,33	1,68			1,28	1,40	1,42
					0,71/2,26	0,83/2,10
1,27	1,60	0,50/2,40			1,44	1,64	1,65
						0,78/2,18	0,84/2,08
1,22	1,53		0,57/2,35	0,63/2,31		1,67	1,97	1,99
					0,68/2,28		0,81/2,13	0,86/2,05
≤ 1,20	≤ 1,50					0,73/2,25	2,00	2,56
							0,77/2,20	0,83/2,10