Экспериментальные исследования на физической модели МГД-насоса жидкого металла

Благодарность. Исследование осуществлено при поддержке КГАУ «Красноярский краевой фонд поддержки научной и научно-технической деятельности» в рамках проекта «Разработка концепции научнотехнологического развития Красноярского края» № 2022112709166.

Цитирование: Кижаев И. В. Экспериментальные исследования на физической модели МГД-насоса жидкого металла / И. В. Кижаев, В. Н. Тимофеев, М. Ю. Хацаюк // Журн. Сиб. федер. ун-та. Техника и технологии, 2023, 16(7). С. 843–856. EDN: SNJMVH материалами, близкими по свойствам к оригинальным, в определенном масштабе к натуральному прототипу. Данный метод более экономичен и менее трудоемок.

Физическая модель МГД‑насоса

В качестве моделирующего металла использован эвтектический сплав на основе Галлия Ga62 In25 Sn13 (галлий 62 %, индий 25 %, олово 13 %, температура плавления T пл = 5 ^oC), основные параметры которого представлены в табл. 1. Данный сплав имеет близкие к жидкому алюминию динамическую вязкость η Ал = 0,001 кг/(м · с), η Эв = 0,0014 кг/(м · с) и удельное электрическое сопротивление γ_Ал = 2,4 · 10^–7 Ом · м , γ_Эв = 2,72 · 10^–7 Ом · м . Что позволяет сделать вывод о подобии электромагнитных и гидродинамических процессов, протекающих в оригинале и в физической модели МГД-насоса.

Масштаб можно определить из условия соблюдения подобия оригинала и модели [15].

^oa)Yo ' ^o ^mV Ут ' ^m ' (1)

где l_o , l_m – характерные размеры оригинала и модели соответственно, м ; γ_o , γ_m – удельные электрические сопротивления расплава в оригинале и расплава в модели, Ом · м ; ω o , ω m – циклические частоты электромагнитных полей в оригинале и в модели, Гц .

Согласно условию (1), при значениях для оригинала l o = 1 м ; γ o = 2,4 · 10^–7 Ом · м ; ω o = 2 π f = 2 · 3,14 · 2 = 12,56 Гц , безразмерный коэффициент добротности для оригинала будет равен ko = lо ^Yo " ^o = 0,0018. Для выполнения данного условия необходимо подобрать частоту и радиус модели при заданном γ_m = 2,72 · 10^–7 Ом · м .

Частота питающего напряжения для модели принята 50 Гц , что позволяет снизить затраты на ее изготовление и последующее исследование. Соответственно, для использования данной конструкции насоса при промышленной частоте придется сохранить относительно большие габариты. При l_m = 0,3 м коэффициент добротности модели будет равен k_м = l_m ■^Ym " ^m = 0,0019. Исходя из этого линейный масштаб модели к оригиналу выбран 1:3.

Так как плоские линейные индукционные насосы представляют собой индукторы с разомкнутым магнитопроводом, помимо бегущего магнитного поля они создают в активной зоне пульсирующие магнитные поля. Эти пульсирующие поля индуктируют в жидком металле токи, приводящие к дополнительным потерям мощности, а также увеличивающие несимме-

Таблица 1. Свойства моделирующего эвтектического сплава

Table 1. Properties of the modeling eutectic alloy

Эвтектический сплав на основе Галлия (GaInSt) Удельное электрическое сопротивление 2,72 · 10–7 Ом · м Относительная магнитная проницаемость 1 Плотность 6200 кг/м3 Теплопроводность 25,3 Вт/(м · К) Теплоемкость 364 Дж/(кг · С) Динамическая вязкость 0,0014 кг/(м · с) тричную нагрузку фаз. Для компенсации данных эффектов был предложен индуктор линейной индукционной машины [15]. С учетом выбранного масштаба индуктора МГД-насоса, состоящего из магнитопровода и катушечных секций, его основные геометрические размеры представлены на рис. 1, а также в табл. 2.

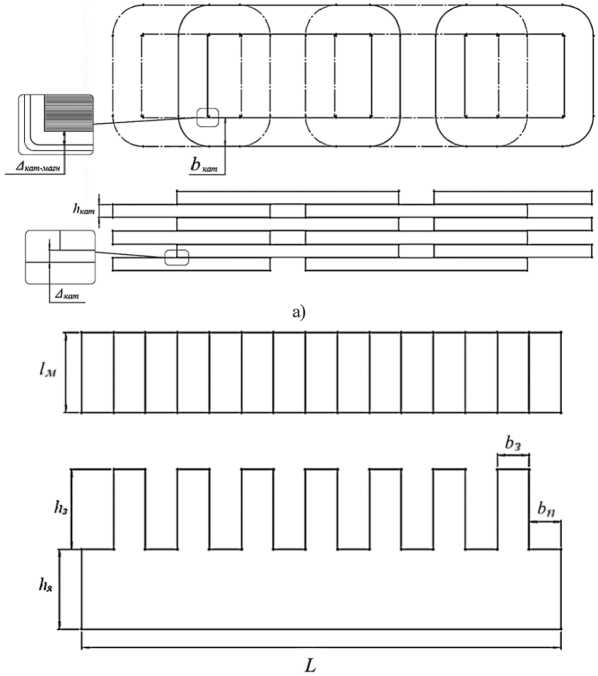
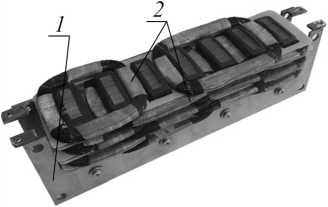
Модель индуктора плоского линейного индукционного насоса с перекрещивающимися обмотками представлена на рис. 2. Состоит данное устройство из магнитопровода 1 и обмоточных секций 2. Магнитопровод модели представляет собoй пакет, набранный из 140 пластин листовой электротехнической стали толщиной 0,35 мм .

Обмотка индуктора состоит из катушек, где в качестве обмоточного провода использовался эмалированный теплостойкий высокопрочный провод ПЭТВ-2 диаметром 1 мм . Температурный индекс провода – ТИ-130. Может эксплуатироваться при температуре окружающей среды от –60 ^оС до +200 ^оС . Намотка осуществлялась механически с помощью намоточного станка на специально-изготовленные формы. Далее полученные обмотки пропитывались лаком с последующим запеканием в печи при температуре +160 ^оС для удержания формы.

б)

Рис. 1. Геометрия и основные размеры индукторов МГД-насоса

Fig. 1. Geometry and main dimensions of the inductors of the MHD pump

Таблица 2. Геометрические размеры индуктора МГД-насоса

Table 2. Geometric dimensions of the MHD pump inductor

Описание	Обозначение	Значение
Высота зубца	h з	50 мм
Высота ярма	h я	50 мм
Длина зубца	b з	20 мм
Длина паза	b п	20 мм
Ширина магнитопровода	lм	50 мм
Длина магнитопровода	L	300 мм
Высота катушки	кат	8 мм
Длина катушки	b кат	18 мм
Зазор между катушками	Δ кат	1 мм
Зазор между катушкой и магнитопроводом	Δ кат-магн	1 мм

Рис. 2. Индуктор двустороннего МГД-насоса в сборе (а), магнитопровод (б), катушки МГД-насоса (в)

Fig. 2. Inductor of the double-sided MHD pump assembly (a), magnetic circuit (б), coils of the MHD pump (в)

Полученные катушки укладываются секциями, в каждой из которых два слоя катушек. Каждая секция обмотки состоит из двух катушек, охватывающих по три зубца магнитопровода и размещенных в шести пазах активной зоны индуктора, и двух крайних катушек, охватывающих по два зубца магнитопровода. При этом если в одном слое секции часть крайней катушки расположена в пазу вне активной зоны индуктора, то во втором слое секции часть крайней катушки располагается в противоположном пазу вне активной зоны.

Данный конструкционный тип укладки обмоток с воздушными каналами и чередованием слоев по высоте паза позволяет охлаждать ее и выравнивать индуктивное сопротивление фаз. Что сказывается на возможности использовать в кратковременном режиме плотности тока вплоть до 10 А/мм² .

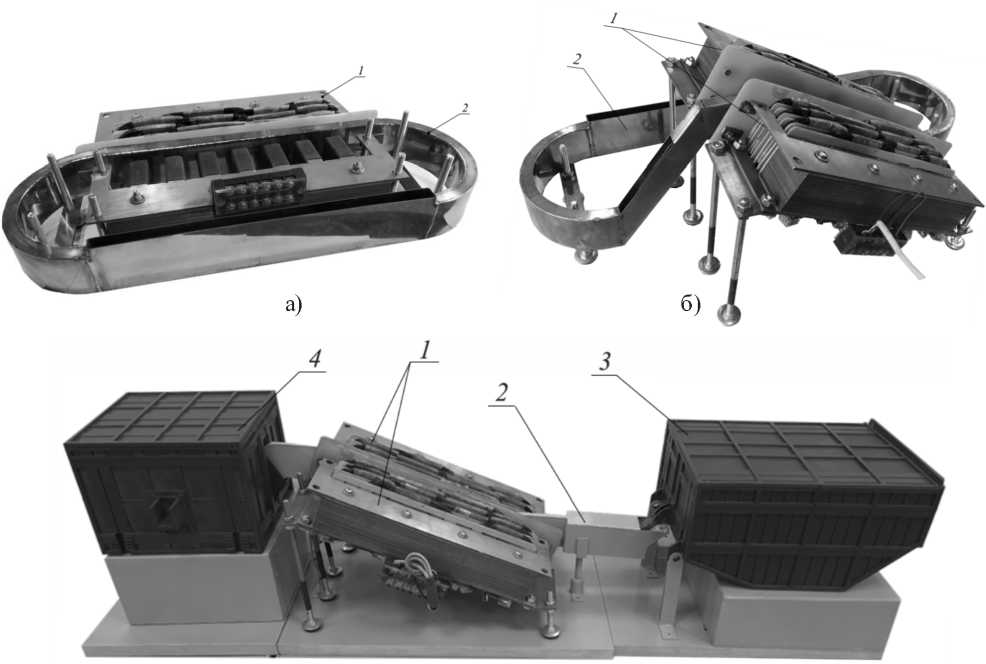
Для более подробной оценки работоспособности МГД-насоса в условиях, приближенных к реальным, изготовлены 3 вида канальной части. Различные конструктивные исполнения (рис. 3) использованы для измерения скоростей жидкого эвтектического сплава (рис. 3а), для построения напорно-расходной характеристики (рис. 3б), для моделирования рабочего процесса транспортировки в лабораторной установке системы «миксер – печь» (рис. 3в).

В качестве источника питания индукторов МГД-насоса использовался трехфазный лабораторный автотрансформатор (ЛАТР) номинальной мощностью 15 КВА . На вход ЛАТРа подается синусоидальное трехфазное напряжение 380 В .

На выходе для измерения энергетических характеристик устанавливается измерительный комплект К505, который позволяет измерять токи, напряжения и мощности на каждую фазу. Верификация математической модели проводилась с помощью сравнения интегральных характеристик экспериментальной и математическими моделями. Обмотки каждого индуктора соединены в звезду, а обмотки индукторов соединены параллельно. Схема включения обмоток к источнику питания будет иметь вид, представленный на рис. 4.

Полученные в ходе эксперимента и расчетные интегральные параметры МГД-насоса представлены в табл. 3. Измерения проводились по фазным токам с шагом в 5 А . Расчетные данные были получены при помощи разработанной компьютерной модели, описанной в предыдущих главах данной работы. Эксперимент № 4 с током в катушках 20 А был выполнен, однако К505

в)

Рис. 3. Физические модели с различными исполнениями канальной части, где: 1 – индукторы МГД-насоса;

2 – канальная часть; 3 – модель печи переплава; 4 – модель миксера

Fig. 3. Physical models with different versions of the channel part, where: 1 – MHD pump inductor; 2 – channel part; 3 – remelting furnace model; 4 – mixer model

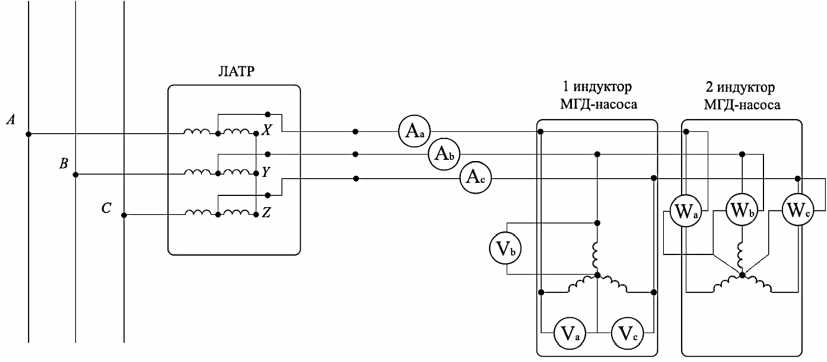
Рис. 4. Схема подключения обмоток МГД-насоса к источнику питания

Fig. 4. Scheme of connecting the windings of the MHD pump to the power source

Таблица 3. Экспериментальные и расчетные интегральные параметры

Table 3. Experimental and calculated integral parameters

Экспериментальные данные Расчетные данные Фаза Uф, В Iф, А P„„ Rt инд, т cosφ Uф, В Iф, А Р,,,,„ Rt инд,  т cosφ 1 эксперимент А 35 5 46 0,26 34,7 5 44,9 0,259 В 39 5 48 0,24 39,2 5 47,4 0,242 С 83 6 97 0,2 69,5 5 67,7 0,195 2 эксперимент А 69 10 183 0,26 69,4 10 179,7 0,259 В 78 10 190 0,24 78,4 10 189,7 0,242 С 139 11 300 0,2 139 10 271 0,195 3 эксперимент А 104 15 405 0,26 104,1 15 404,4 0,259 В 120 15 432 0,24 117,6 15 424,8 0,242 С 215 15 645 0,2 208,5 15 609,8 0,195 4 эксперимент А - - - 0,26 138,8 20 718,9 0,259 В - - - 0,24 156,8 20 758,9 0,242 С - - - 0,2 278 20 1084,2 0,195 не позволяет измерять токи свыше 15 А без использования трансформатора тока. Соответственно, экспериментальные данные для измерений в табл. 3 отсутствуют.

Средние расхождения между экспериментальными и расчетными данными в пределах 5 %, что позволяет сделать вывод об адекватности математических моделей [16] и использовать их для дальнейшего проектирования установок с аналогичным конструктивным исполнением.

а)

б)

в)

Journal of Siberian Federal University. Engineering & Technologies 2023 16(7): 843–856 Исследование гидродинамических и тепловых процессов в экспериментальной установке и их сравнение с результатами математического моделирования

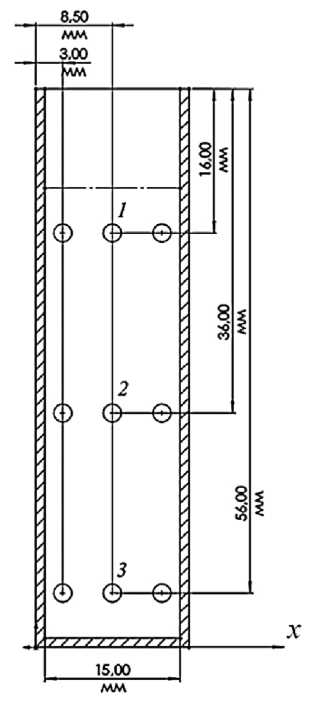
Рис. 5. Основные размеры и положение контрольных точек для измерения

Fig. 5. Main dimensions and position of control points for measurement

Верификация математической модели проводилась путем сравнения результатов математического моделирования гидродинамических и тепловых процессов с экспериментальными данными, полученными в результате измерений. Сравнение в гидродинамической части будет осуществляться измерением скоростей жидкого металла, а тепловую задачу будем сравнивать по нагреву металла и обмоточных секций. Измерения скоростей жидкого металла проводились с помощью ультразвуковых датчиков скорости.

Основные размеры и геометрия исследуемой области канальной части представлены на рис. 5. Ток в индукторах МГД-насоса 15 А , с частотой 50 Гц . Измерения скоростей проводились в девяти основных точках, расположенных на поверхности расплава 1 в центре 2 и в нижней части канала 3.

На созданной математической модели, аналогичной по геометрическим и энергетическим параметрам экспериментальной, решена электромагнитная, гидродинамическая и тепловая задачи. Результаты математического моделирования были сравнены с результатами, полученными в ходе эксперимента.

При подключении обмоток МГД-насоса к сети напряжения в обзорном окне (рис. 6) видно, как эвтектический сплав резко «вытягивается» из одной части канала в другую. Течение при этом имеет несущественные завихрения, а в установившемся режиме принимает ламинарный вид.

Рис. 6. Процесс «вытягивания» расплава при включении индукторов МГД-насоса

Fig. 6. The process of “pulling” the melt when the inductors of the MHD pump are turned on

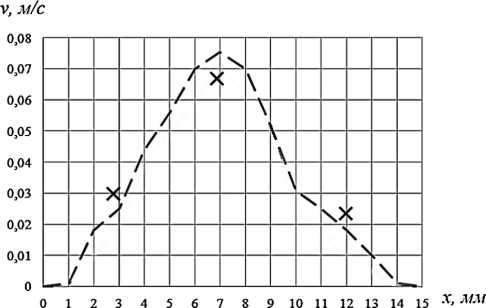
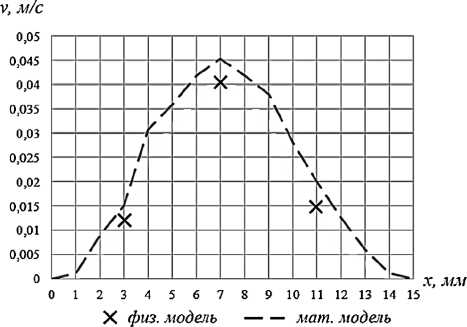
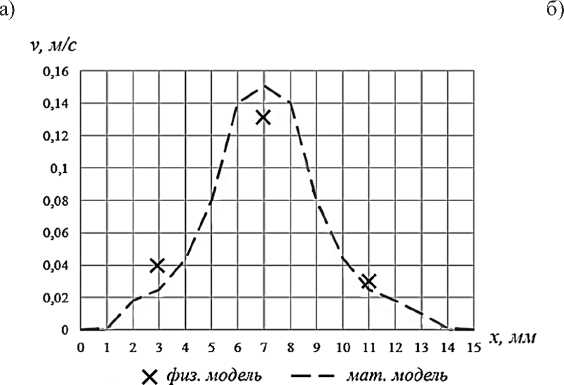
На рис. 7 представлены графики распределения осредненной скорости на контрольных точках, где точки обозначают результаты измерений, а прерывистая линия – результаты математического моделирования

В результате измерений сравнение результатов показало, что отклонение составляет не более 10 %. Однако это не говорит о достоверности полученных результатов предложенной математической модели, так как измерение скорости ультразвуковым датчиком в локальных участках с завихрениями на физической модели достаточно проблематично ввиду сложного характера течения.

Для проверки адекватности результатов решения тепловой задачи в экспериментальной модели была выполнена процедура измерения температур металла в канале и катушечных секциях. Для измерения использовался цифровой термометр с выносным датчиком температуры, максимально допустимая температура которого 230 ^о С . Полученные показания температур приведены на рис. 8, 9.

в)

Рис. 7. Осредненные во времени значения скорости в контрольных точках: а – в верхней части канала; б – в нижней части канала; в – в центральной части канала

• Fig. 7.    Time-averaged velocity values at control points: a – in the upper part of the channel; б – in the lower part of the channel; в – in the central part of the channel

а)                                                                   б)

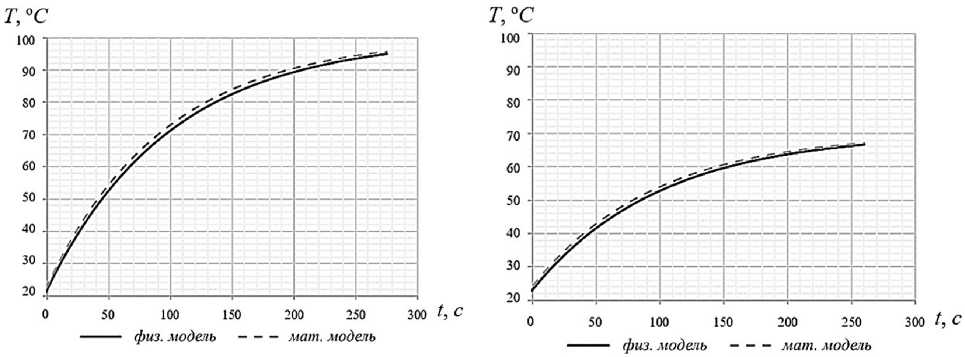
Рис. 8. Кривая нагрева обмоток МГД-насоса при токе в обмотке 15 А: а – без применения активного охлаждения; б – с применением активного воздушного охлаждения

• Fig. 8.    Heating curve of the windings of the MHD pump at a current in the winding of 15 A: a – without the use of active cooling; б – with the use of active air cooling

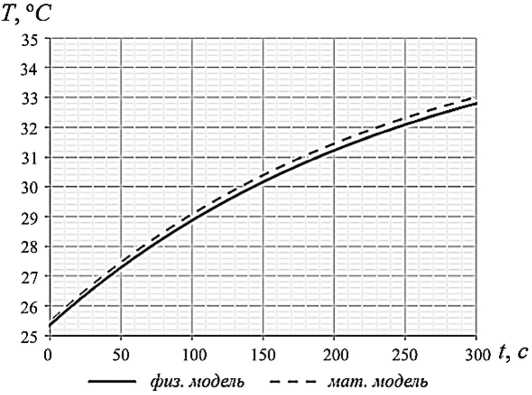
Рис. 9. Кривая нагрева эвтектического низкотемпературного сплава

Fig. 9. Heating curve of eutectic low temperature alloy

Из построенных кривых можно сделать вывод о том, что результаты математического моделирования аналогичны измеренным данным на физической модели. Это, в свою очередь, доказывает достоверность и адекватность тепловой математической модели МГД-насоса.

Приняв геометрические размеры математической модели постоянными, было произведено моделирование при различных углах наклона канальной части, что позволило определить максимальную высоту подъема жидкого металла. При этом с преодолением гидростатического давления жидкого металла максимально возможный подъем составляет 600 мм .

Расположение контрольных точек для измерения скоростей ультразвуковым датчиком сохранилось, согласно рис. 5. Однако на данной модели измерения скорости в канальной части проводились не в непосредственной близости к индукторам МГД-насоса, а в противополож-– 852 – ной части, где течение принимает более ламинарный вид. Так как в участке рядом с индукторами образуется свободная поверхность жидкого металла, в которой измерение скорости затруднительно. Полученные результаты (рис. 11, 12) также имеют схожий вид и характер, как и в случае плоского замкнутого канала.

Точками обозначены распределения скорости расплава в канале физической модели, прерывистой линией – распределение скорости в математической модели. Максимум скорости

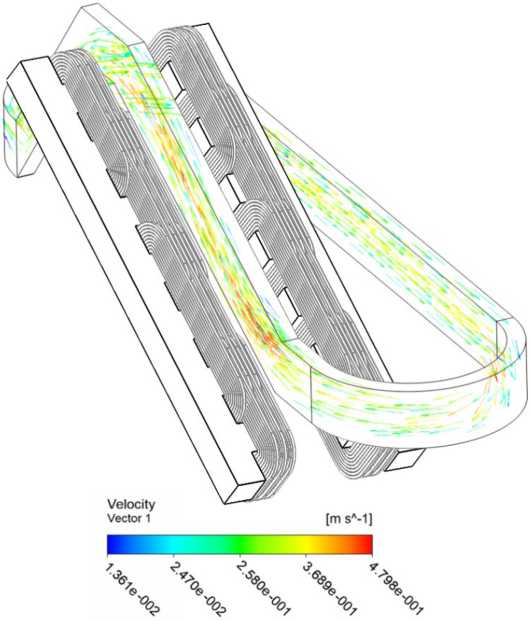
Рис. 10. Векторное поле скоростей жидкого металла в канальной части

Fig. 10. Vector field of liquid metal velocities in the channel part и, м/с

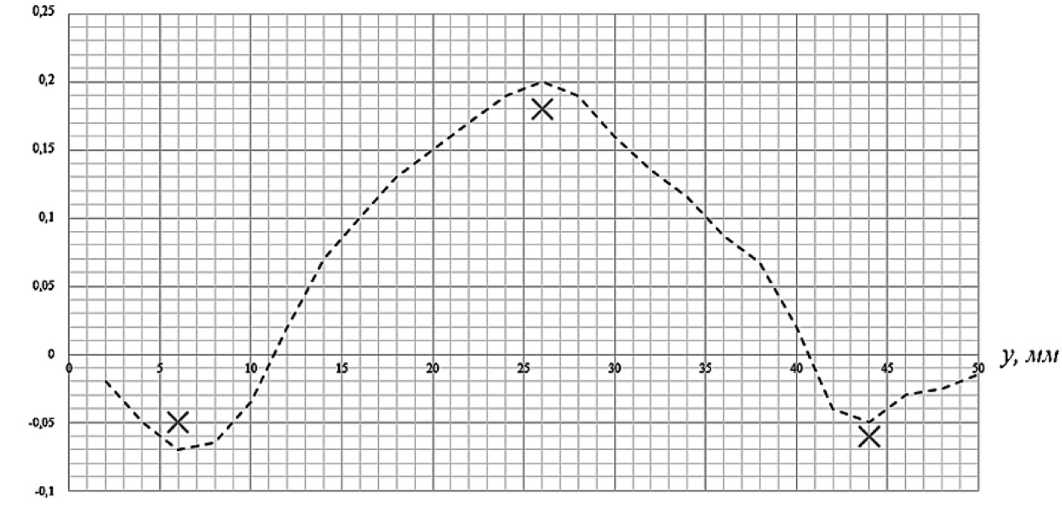
Рис. 11. График осредненной скорости в центральной части канала по высоте y

Fig. 11. Graph of the average velocity in the central part of the channel along the height y

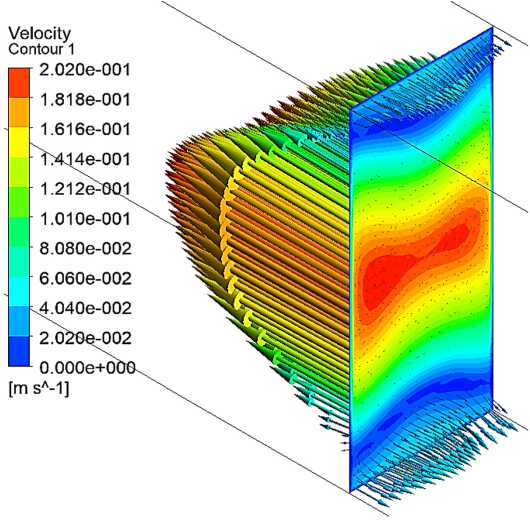
Рис. 12. Профиль скорости в поперечном сечении канальной части

Fig. 12. Velocity profile in the cross section of the channel part также располагается в центральной части канала, что соответствует данным, полученным в предыдущем эксперименте.

Сравнение результатов показало, что отклонение величин, полученных в ходе математического моделирования, от экспериментальных данных также не превышает 10 %, что говорит о достаточной достоверности получаемых гидродинамических потоков с использованием предложенной математической модели.

Выводы

Распределения скоростей жидкого металла в каналах математической и физической моделей схожи по характеру и средним величинам. Средняя разность результатов между моделями равна 10 %. Это обусловлено пренебрежением в математической модели конструктивными элементами, такими как щеки для стягивания и шпильки. Также немаловажную роль в разности результатов сыграл коэффициент заполнения пазов. В математической модели данный коэффициент равен 50 %, когда в физической модели коэффициент заполнения равен 40 %, соответственно, линейная токовая нагрузка в физической модели несколько ниже, чем в математической.

Результаты же теплового эксперимента получились идентичными в физической и математической моделях. Разность результатов менее 5 %, что свидетельствует адекватности построенной тепловой модели. Применение активного воздушного охлаждения позволило повысить величину линейной токовой нагрузки и развиваемое усилие, соответственно, однако применение в таком энергетическом режиме крайне ограничено по времени.

Физическая модель позволила верифицировать результаты математического моделирования, что позволяет использовать ее для будущего проектирования опытно-промышленных образцов МГД-насосов.