Экспоненциальные оценки сумм многомерных случайных величин

Работа с суммой многомерных случайных величин является одной из сложных задач статистического анализа и теории вероятностей. Оценка и анализ поведения многомерных случайных величин необходимы в различных областях, включая телекоммуникации, финансы, биологию и экономику. Экспоненциальные оценки многомерных сумм обеспечивают высокоточные вычисления, которые полезны для оценки вероятностей экстремальных значений случайных сумм.

Экспоненциальные оценки являются удобным методом оценки случайных сумм с высокой точностью, и на основании их вида делаются статистические и вероятностные выводы. В этой статье рассматриваются классические оценки, такие как оценки Чернова и Хёфдинга, расхождение Кульбака-Лейблера и их приложения.

Многомерные случайные переменные

Сумма многомерных случайных величин играет важную роль в математическом моделировании. Допустим, у нас есть X=(^Л,..д,) является векторной случайной величиной, причем каждая случайная величина независима и имеет одинаковое распределение. Такое суммирование удобно при рассмотрении общего поведения нескольких переменных.

Если каждый среднее значение (ожидание) случайной величины E[X_t] = P если есть, то его собирают ^Sn -^ +^2⁺- + ^иесли есть, то его собирают

Elsn] = "-Vбудет равен. И дисперсия суммы Var^S^ = n • Var(X:) определяется. Но оценка вероятности отклонения суммы от своего распределения с помощью экспоненциальных оценок позволяет нам контролировать степень неопределенности.

Концепция экспоненциального ценообразования

Экспоненциальные оценки широко используются в теории вероятностей и позволяют оценить вероятность того, что случайные величины примут выбросные значения, с помощью экспоненциальных функций. Этот метод полезен для быстрого расчета вероятности большого количества случайных сумм. Одним из наиболее распространенных методов является оценка Чернова и ее адаптация для многомерных сумм.

Оценка Чернова. Оценка Чернова широко используется для экспоненциальной оценки высоких вероятностей. Чтобы проиллюстрировать это, давайте рассмотрим следующую ситуацию: предположим, x^x^x,, являются независимыми случайными величинами, каждая £M=/> имеет ожидание. Вот и все s„XX верхний предел для

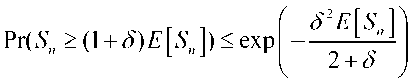
здесь, ^ > о . Эта оценка экспоненциально снижает вероятность того, что случайная сумма даст значения, превышающие ожидаемые. Оценка Чернова — удобный метод оценки высоких вероятностей больших случайных сумм. Оценка Хеффдинга. Оценка Хеффдинга также является разновидностью экспоненциальной оценки и используется для оценки вероятности того, что случайная сумма значительно отклоняется от ожидаемого значения. Давайте, предположим x^x^x,,являются независимыми случайными величинами, и каждая определенный[ai’bi] быть ограничено. Общий S.^X!следующая оценка подходит для:

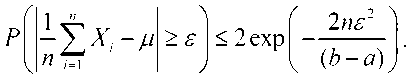
Эта оценка сильно ограничивает вероятность значительного отклонения случайной суммы от ее ожидаемого значения и позволяет получать точные результаты. Оценщик Хеффдинга обеспечивает удобную и точную оценку при работе со случайными суммами большой выборки.

Расхождение Кульбака-Лейблера

Дивергенция Кульбака-Лейблера используется для получения более точного значения экспоненциальных оценок. Это расхождение измеряет расстояние между двумя распределениями и используется для оценки случайных сумм. Если P и Q являются распределениями вероятностей, их расхождение Кульбака-Лейблера выражается следующим образом:

°«(/’l|y) = ZP('-)iog^ .

леА

Дивергенцию Кульбака-Лейблера можно использовать для более точного различения многомерных сумм, что позволяет проводить более точные статистические оценки. На практике экспоненциальная оценка многомерных сумм с использованием этого расхождения дает более точные результаты.

Практическое применение

Многомерные случайные суммы и экспоненциальные оценки широко используются в таких областях, как телекоммуникации, финансы и инженерия. Например, в телекоммуникационной системе уровень шума в процессе передачи сигнала проявляется в виде случайных сумм. Экспоненциальные оценки можно использовать для оценки вероятности того, что сигнал будет передан с более низким или более высоким качеством, чем ожидалось. Кроме того, при оценке финансовых рисков экспоненциальные оценки используются для расчета вероятности значительного уменьшения или увеличения доходности акций или стоимости активов.

Заключение

Сумма многомерных случайных величин может быть оценена с высокой точностью с помощью экспоненциальных оценок. Такие методы, как оценки Чернова и Хеффдинга, полезны для точной оценки высоких вероятностей. Использование дивергенции Кульбака-Лейблера позволяет получить более точное значение экспоненциальных оценок. Эти методы используются при решении задач, связанных с многомерными случайными суммами, и в статистическом анализе с высокой неопределенностью.