Экспресс-метод вибродиагностики силы сухого трения при вынужденных колебаниях динамических систем

В технике существует целый класс механических систем с контактирующими и трущимися элементами, в которых действующие силы сухого трения существенно влияют на динамические процессы и обладают полезной и объективной информативностью их технического состояния. Поэтому действующие силы сухого трения могут быть использованы в качестве диагностических признаков для оценки технического состояния такого класса объектов, в том числе на дихотомическом уровне («годен» - «негоден»). Перспективность такого подхода обусловлена непосредственной однозначной связью между нарушениями функционирования объекта и величиной диссипативных потерь в его колебательной системе, а также оперативностью диагностирования. Количественная идентификация диссипативных параметров колебательных систем необходима и при построении их математических моделей. Для упругих систем, которые при эксплуатации функционируют в околорезонансных режимах или непосредственно подвергаются резонансным колебаниям, изучение их демпфирующих свойств приобретает исключительно важное значение. Таким образом, разработка обоснованных методов определения диссипативных характеристик реальных упругих механических систем является актуальной задачей.

Большинство известных методов идентификации диссипативных параметров сухого трения имеют трудоёмкие алгоритмы диагностических процедур или сложную и дорогостоящую

аппаратурную реализацию [1-6]. Для построения процедуры идентификации сил сухого трения рассмотрим особенности динамического поведения данного вида систем при вынужденных колебаниях под действием гармонической силы (рис. 1).

Рис. 1. Расчетная динамическая схема системы с сухим трением

Для исследования рассматриваемой системы будем использовать среду визуального математического моделирования динамических систем Simulink/MATLAB. Блок-схема Simulink-модели представлена на рис. 2. Более подробное описание модели и её тестирование дано в [7].

Как следует из анализа временных законов изменения ускорения (см. рис. 3 и рис .4) при любых режимах движения в системе с сухим трением наблюдаются скачки ускорения, возникающие вдали от положения равновесия.

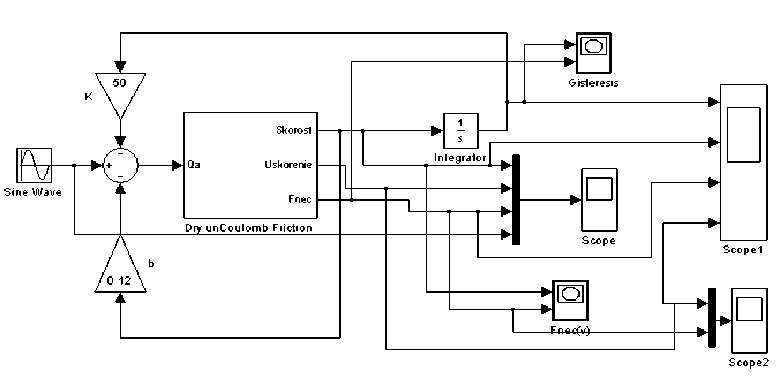
Рис. 2. Блок-схема Simulink-модели динамической системы с сухим трением

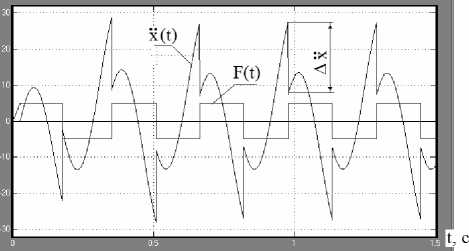
Рис. 3. Виброграмма ускорения и график изменения силы сухого трения во времени системы с сухим трением при безостановочном режиме движения (ω=20 с^{^1}, F=5Н, P=10 Н, b=0,12 Нc/м, k=50 Н/м, m=0,5 кг)

В режимах движения с продолжительными остановками закон изменения силы сухого трения усложняется – в момент остановок уравнение силового равновесия принимает вид:

k • A - F* = P0 • cos(m • t + ф)

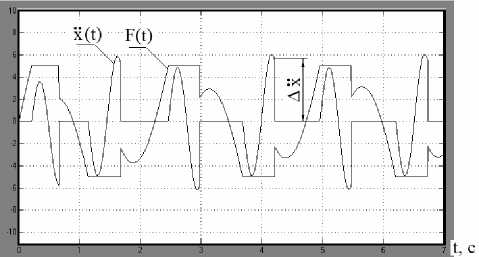
Рис. 4. Виброграмма ускорения и график изменения силы сухого трения во времени системы с сухим трением при остановочном режиме движения (ω=2,5 с^{^1}, F=5Н, P=10 Н, b=0,12 Нc/м, k=50 Н/м, m=0,5 кг)

и сила сухого трения F* «копирует» вынуждающую силу P cos (ωt + φ). При этом величина скачков ускорения уже меньше 2 F / m (рис. 4).

Используя количественную обусловленность величины скачка ускорения силой сухого трения при безостановочных режимах движения в соответствии с выражением (1), представляется возможным определить силу сухого трения, действующую в колебательной системе [8]:

Дх • m F =

Функция чувствительности решающего алгоритма:

K = 9Дх = 2 = dF ~ m

При безостановочных режимах движения, когда сила сухого трения представляет собой «прямоугольный синус» с амплитудой «F», величина скачка ускорения равна (рис. 3):

дх =

2 • F

m

является гиперболической функцией массы колебательной системы. Следовательно, метод идентификации силы сухого трения будет тем чувствительней, чем меньше масса идентифицируемого объекта. Примерный алгоритм экспресс-метода определения силы сухого трения при вынужденных колебаниях динамической системы представлен в таблице 1.

В качестве апробации рассмотренного экспресс-метода диагностирования сухого трения при вынужденных колебаниях динамической системы на рис. 5 показана экспериментальная

осциллограмма виброускорений упруго установленного подвижного элемента диагностического прибора – индентора, в направляющих которого действовали силы сухого трения и силы вязкого сопротивления.

Таблица 1. Алгоритм экспресс-метода количественного определения силы сухого трения

Шаг 1.	Возбудить вынужденные колебания идентифицируемой системы с безостановочным режимом движения и определить частоту резонанса ω / p ≈1, где p – собственная частота.
Шаг 2.	Установить частоту вибровозбуждения в интервале ω / p =1,1-2,0
Шаг 3.	По временному закону изменения виброускорения определить величину скачка Δ & x & .
Шаг 4.	Определить массу колебательной системы m
Шаг 5.	Рассчитать величину силы сухого кулонова трения по формуле (3).
Шаг 6.	Повторить процедуру идентификации, начиная с шага 2, для получения статистической информации и оценки погрешности.

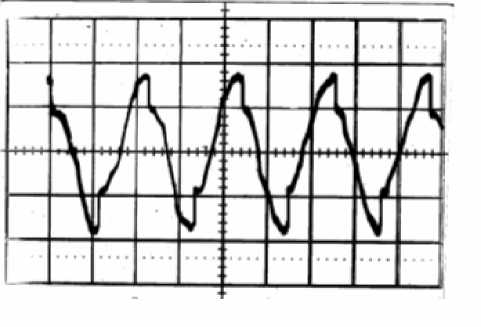
Рис. 5. Экспериментальная осциллограмма виброускорений динамической системы с сухим трением

Измеренные величины скачков ускорения Δ & x & и определенная из независимого эксперимента масса m колебательной системы позволили определить величину действующей силы сухого трения с относительной погрешностью, не превышающей 8%, при высокой оперативности и простоте аппаратурной реализации. Это позволяет рассматривать данный способ как эффективный экспресс-метод оперативного диагностирования величины сухого трения в колебательных системах при их вынужденных колебаниях.

Выводы: достоинствами рассмотренного метода идентификации силы сухого трения являются: 100% точность решающего алгоритма; инвариантность к действующим силам вязкого сопротивления; возможность идентификации при неполноте информации о виде вибровозбуждения; нетребовательность к источнику возбуждения колебаний; простота аппаратурной реализации; высокая оперативность и производительность идентификации вплоть до возможности организации процедуры в реальном масштабе времени. К недостаткам метода можно отнести некоторую помехо-восприимчивость, обусловленную влиянием шумов на измерение скачка ускорения по виброграмме.

Работа выполнена в рамках реализации Федеральной целевой программы «Научные и научнопедагогические кадры инновационной России» на 2009-2013 годы по проблеме «Исследование закономерностей движения и идентификация динамических параметров механических систем с сухим некулоно-вым трением» (гос. контракт № П2243, шифр НК 422П).