Экспресс-оценка усталостной прочности композитных фланцев методом инфракрасной термографии

ВЕСТНИК ПНИПУ. МЕХАНИКА № 4, 2024PNRPU MECHANICS BULLETIN

В последние годы все больше внимания уделяется изучению сопротивления усталостному разрушению полимерных композиционных материалов (ПКМ). Это обусловлено современной тенденцией применения этих материалов для изготовления высоконагруженных, подверженных вибрациям элементах конструкций, таких как детали и узлы ветрогенераторов, автомобилей и судов (см., например [1]). В наибольшей степени проблема усталостной прочности ПКМ актуальна для обеспечения надежности и безопасности в авиастроении, где постоянно увеличивается доля элементов из слоистых угле- и стеклопластиков [2–7].

Несмотря на то, что усталость композитов изучается во всем мире десятки лет, при проектировании ответственных изделий обычно приходится проводить специальные исследования и испытания, чтобы получить недостающие характеристики сопротивления усталостному разрушению. Причина в многообразии материалов наполнителя и матрицы, схем армирования, влиянии технологических и эксплуатационных факторов и, как следствие, многообразии механизмов разрушения [8–12]. У наиболее распространенных слоистых стекло- и углепластиков (GFRP и CFRP) выделяют несколько стадий усталостного разрушения: появление микротрещин в матрице, расслоения на границах матрицы и волокна, расслоения ламината, разрыв армирующих волокон [13].

Для определения характеристик сопротивления усталости композиционных материалов обычно проводят испытания образцов при циклическом нагружении с по- строением кривой усталости и определением ограниченного предела выносливости в соответствии со стандартами [14; 15]. Такой подход требует проведения длительных дорогостоящих испытаний большого количества образцов при различных уровнях нагрузки. Это ограничивает возможности оптимизации схем армирования, проверки конструктивных и технологических решений при проектировании изделий, затягивает сроки и стоимость разработки. Для приближенной экспресс-оценки предела выносливости металлов применяют ускоренные методы Про, Эномото, Локатти и др. [16– 19]. Применительно к металлам был разработан подход к оценке характеристик сопротивления многоцикловой усталости без усталостных испытаний с использованием характеристик рассеяния энергии при циклических деформациях (см., например, [19; 20]).

Для ускоренного определения предела выносливости металлов в работах A.Risitano [21] и M.Luong [22] был предложен термографический метод (IRT-метод, Infra-Red Thermography), основанный на интенсификации саморазогрева образца в процессе нагружения при нагрузках выше предела выносливости вследствие появления и развития усталостных повреждений. Достоверность результатов авторы [21; 22] подтверждают сравнением с пределами выносливости, полученными путем стандартных усталостных испытаний. В качестве главного преимущества метода IRT перед стандартными усталостными испытаниями отмечается, что он позволяет получить предел выносливости за короткое время на небольшом количестве образцов.

Метод IRT с некоторыми вариациями успешно применялся не только к металлам [23–26], но и к различным полимерным композиционным материалам: слоистым термореактивным углепластикам [27], 3D-ар-мированным углепластикам [28], стеклопластикам [29], термопластам [30; 31], гибридным композитам [32]. В работе [28] перечислены основные механизмы накопления усталостных повреждений, вызывающие рассеивание энергии и саморазогрев армированных композитов при циклическом нагружении: вязкоупругое деформирование материала матрицы, растрескивание матрицы, трение на поверхности раздела волокон и матрицы, переориентация волокон, разрушение волокон.

Особую роль в усталостной прочности слоистых угле- и стеклопластиков играют конструктивные и технологические факторы. Даже если доступны полученные из испытаний образцов характеристики усталостной прочности материала, их использование при проектировании конструкций из этого материала ограничено и часто требует дополнительных исследований [13; 18; 38]. Причина в том, что условия нагружения волокон и матрицы в образцах и конструктивных элементах могут существенно различаться, особенно в локальных зонах изгиба слоев ламината, утолщений, отверстий, соединений. Такие локальные зоны имеются, например, у подкрепляющих элементов оболочек, фланцев и т.д. Другая причина в том, что даже одинаковые технологии изготовления образцов и конструктивных элементов не гарантируют совпадение их механических характеристик. Поэтому в ответственных случаях для определения характеристик сопротивления усталостному разрушению приходится проводить испытания натурных деталей или типовых конструктивных элементов (см., например, [39–43]).

В настоящей работе рассматривается усталостная прочность элементов фланцевых соединений, которые широко применяются и часто являются наиболее нагруженными в конструкциях из ПКМ [44–46]. В работах [45; 46] исследовано напряженно-деформированное состояние фланцев композитных оболочек при статическом нагружении. В работе [47] исследованы закономерности разрушения и теплового состояния фланцев углепластиковых оболочек в условиях усталостных испытаний.

Цель настоящего исследования – разработка методики экспресс-оценки предела выносливости фланцев из слоистого композита с использованием метода IRT.

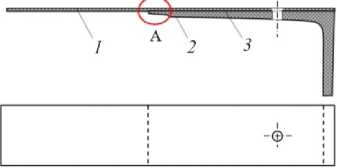
Рис. 1. Образец: 1 – оболочка; 2 – фланец; 3 – клеевой слой

Fig. 1. The sample: 1 – shell; 2 – flange; 3 – adhesive layer

Методика исследования

Объектом исследования в настоящей работе является типичная оболочка с Г-образным фланцем, который служит для ее соединения с соседними деталями [44]. Образец для исследований представляет собой вырезанный из натурной конструкции прямоугольный в плане фрагмент оболочки с фланцем (рис. 1). Оболочка изготовлена из слоистого углепластика на основе однонаправленной углеродной ткани и эпоксидного связующего, а фланец – на основе равнопрочной ткани; они склеены между собой. Размеры образца 150×40 мм, толщина оболочки около 2 мм.

В процессе эксплуатации конструкция подвергается воздействию вибрации, которая вызывает циклический изгиб фланца 2 (см. рис. 1). Проведенное в работе [47] исследование показало, что разрушение начинается с появления расслоения в зоне А между оболочкой 1 и фланцем 2 (рис. 1) и постепенно распространяется до угла фланца.

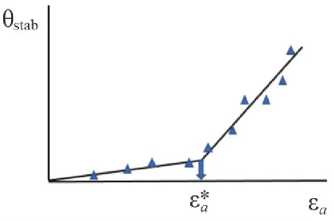
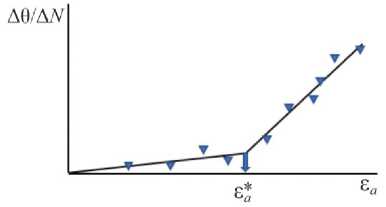
Методика экспресс-оценки предела выносливости фланцев опирается на использование IRT-метода. Этот метод в соответствии с описанием авторов [21; 22] предполагает блочное циклическое нагружение исследуемого образца с регистрацией температуры T на его поверхности. В каждом блоке температура образца вследствие саморазогрева увеличивается, достигая некоторого стабильного для данной нагрузки значения T stab . В блоках с амплитудой нагрузки, превышающей предел выносливости, стабилизационное значение температуры и скорость возрастания температуры в начале блока резко увеличиваются. Этот эффект связан с активизацией тепловыделения при появлении усталостных повреждений. На рис. 2 проиллюстрирована эта процедура: нагрузка в каждом блоке характеризуется амплитудой деформации ε a , нагрев образца – повышением температуры θ = T – T 0 ( T 0 – температура в начале блока), стабилизационным значением θ stab = T stab – T 0 скоростью возрастания температуры в начале блока Δθ/Δ N . Эмпирическая зависимость θ stab от амплитуды деформации в блоке ε a аппроксимируется двумя прямыми, абсцисса точки пересечения которых ε a^* , в соответствии с идей метода, принимается за деформацию, соответствующую пределу выносливости (рис. 3, а ). Аналогичная зависимость для параметра Δθ/Δ N также позволяет определить предел выносливости. В работах авторов метода [21; 22] и работах других авторов (см., например, [27]) для некоторых материалов показано, что полученные обоими способами значения согласуются между собой и с пределом выносливости, полученным в результате стандартных испытаний образцов с построением кривой усталости.

Применение метода инфракрасной термографии для оценки предела выносливости элементов конструкций, в частности исследуемого композитного фланца, требует разработки и верификации конкретной методики. В настоящей работе было необходимо разработать спо- соб нагружения, обосновать выбор количества и параметров блоков нагружения (амплитуда, количество циклов), метода и зоны регистрации температуры поверхности, сравнить эффективность выбора параметров нагрева (θstab или Δθ/ΔN), верифицировать методику по результатам стандартных усталостных испытаний. Перед испытаниями образцов с целью исключения исходных дефектов был проведен неразрушающий контроль ультразвуковым методом на фазированных решетках.

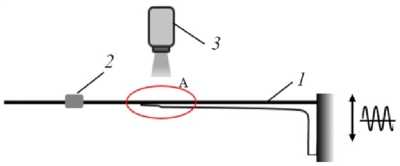
Рис. 4. Схема нагружения образца: 1 – образец;

2 – груз; 3 – инфракрасная камера

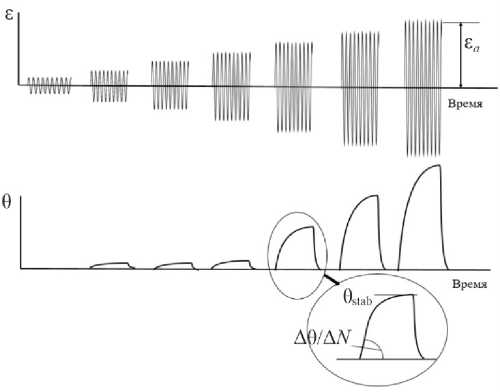
Рис. 2. Блочное нагружение образца в соответствии с методом инфракрасной термографии [21; 22]

Fig. 2. Block loading of the sample in accordance with the IR-thermography method [21; 22]

b

Рис. 3. Определение предела выносливости в соответствии с методом IRT [21; 22] по θ stab ( а ) и Δθ/Δ N ( b ) с ростом нагрузки в блоке

Fig. 3. Determination of the fatigue limit in accordance with the IRT method [21; 22] using θ stab ( a ) and Δθ/Δ N ( b ) with increasing load in the block

Fig. 4. Sample loading scheme: 1 – sample;

2 – cargo; 3 – infrared camera

Блочное циклическое нагружение образца проводили на электродинамическом вибростенде. Образец нагружается силой инерции закрепленного на нем груза при резонансных гармонических колебаниях по изгиб-ной форме (рис. 4). Экспериментальная установка подробно описана в работе [47]. Деформация измеряется тензодатчиком, расположенным на наружной поверхности в зоне А, где начинается усталостное разрушение (см. рис. 4). Она изменяется во времени по гармоническому закону с амплитудой ε a и резонансной частотой f . При такой схеме испытаний обеспечивается симметричный цикл нагружения образца (коэффициент асимметрии цикла R = –1).

Масса груза подбиралась таким образом, чтобы частота колебаний образца в резонансном режиме составляла около 80 Гц. Как показали предварительные эксперименты, при такой частоте колебаний температура саморазогрева образца лежит в пределах 10°. Такая температура не вызывает существенного изменения механических свойств углепластика, при этом она достаточна для инфракрасной термографии.

Регистрацию поля температур на поверхности образца в процессе испытаний проводили с помощью прецизионной инфракрасной камеры NEC TH 9100 WR ProNew с погрешностью ±2 % от показания (см. рис. 4). Для повышения точности измерения температуры перед началом экспериментов поверхность образца покрывали черной матовой краской.

В каждом блоке нагружения задавали и поддерживали постоянной амплитуду деформаций ε a . Количество циклов в блоке на каждом уровне нагрузки устанавливалось индивидуально по достижению стабильной температуры на поверхности образца. При частоте колебаний 80 Гц продолжительность блоков составила 30–50 тысяч циклов. Поле температур на поверхности образца регистрировали в процессе нагружения через каждые 5 тысяч циклов. Каждый новый блок нагружения начинался только после полного остывания образца, перерыв после каждого блока нагружения составлял 30–40 мин.

Для определения предела выносливости были использованы два параметра нагрева образца в каждом цикле нагружения Δθ/Δ N и θ stab . Их определяли по термограммам и осредняли по прямоугольной области размером 40×40 мм на поверхности образца в наиболее

нагруженной зоне А. Далее получали зависимости Δθ/Δ N и θ stab от амплитуды деформации в блоке.

Для определения предела выносливости по зависимости θ stab (ε a ) ее аппроксимировали двумя прямыми, коэффициенты линейной аппроксимации каждой из них определяли методом наименьших квадратов, качество аппроксимации оценивали по коэффициенту детерминации R ² [48]. Значение ε a * , соответствующее пределу выносливости, определяли как абсциссу точки пересечения правой и левой прямых – ветвей аппроксимации.

В зоне пересечения ветвей аппроксимации возникает неопределенность отнесения экспериментальных точек к правой или левой ветвям. Эту неопределенность разрешали подбором по максимальному значению суммарного для обеих ветвей коэффициента детерминации R ² Σ .

Аналогичным образом ε a * определяли по эмпирической зависимости Δθ/Δ N (ε a ) .

Результаты и их обсуждение

В соответствии с описанной выше методикой были исследованы два образца (см. рис. 1). Блочное нагружение образца включало в себя 16 блоков, их параметры приведены в табл. 1. На рис. 5 показаны в качестве примера термограммы образца №1, зарегистрированные в конце блоков нагружения № 3, 8, 15. Пунктиром выделена область А, по которой осредняли Δθ/Δ N и θ stab . На термограммах видно возрастание и локализацию нагрева в области А с увеличением нагрузки в блоке. Повышение температуры поверхности образца в угловой зоне фланца связано, возможно, с менее интенсивным, чем в области А, теплоотводом при колебаниях образца.

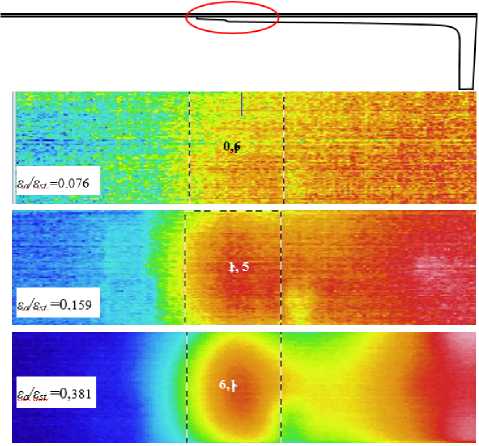
Рис. 5. Термограммы поверхности образца №1, зарегистрированные в конце блоков № 3, 8, 15

Fig. 5. Thermograms of Sample 1 surface registered at the end of blocks No. 3, 8, 15

На рис. 6 показаны зависимости среднего по области А повышения температуры θ образца № 1 с увеличением числа циклов усталостной наработки для различных уровней амплитуды деформации ε a в блоке. Значение ε a отнесено к значению деформации при статическом разрушении материала ε st . На рис. 6 также показан доверительный интервал для измеренной температуры. Температура θ в каждом блоке стабилизируется за 30–50 тысяч циклов. С возрастанием нагрузки в блоке значение θ stab увеличивается. Значение Δθ/Δ N в начале блока, которое вычисляется для всех блоков по первым Δ N= 5000 циклов, также увеличивается с возрастанием нагрузки в блоке. Определенные по термограммам значения θ stab и Δθ/Δ N для всех реализованных блоков нагружения приведены в табл. 1.

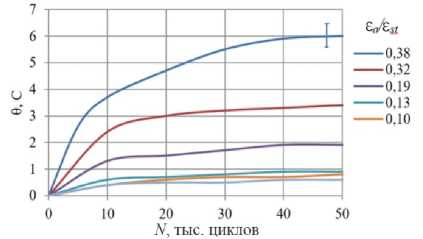
Рис. 6. Повышение средней по области А температуры θ образца №1при различных значениях амплитуды деформации в блоке ε a /ε st

• Fig. 6.    An increase of the average temperature θ of Sample 1 in the A region at different values of the deformation amplitude in the block ε a /ε st

Таблица 1

Характеристики нагрева поверхности образца №1 в реализованных блоках нагружения

Table 1

Characteristics of Sample 1 surface heating in realized loading blocks

№ блока	ε a /ε st	N , циклов	θ stab , град	Δθ/Δ N * 10–3, град/цикл
1	0,0509	100 000	0,6	0,02
2	0,0636	70 000	0,4	0,02
3	0,0763	60 000	0,6	0,04
4	0,0890	60 000	0,8	0,03
5	0,1017	80 000	0,9	0,04
6	0,1271	50 000	0,9	0,06
7	0,1398	40 000	0,9	0,06
8	0,1589	60 000	1,5	0,07
9	0,1907	60 000	1,9	0,13
10	0,2225	60 000	2,1	0,15
11	0,2543	70 000	3,2	0,21
12	0,2860	60 000	3,1	0,21
13	0,3178	60 000	3,4	0,24
14	0,3496	100 000	5,6	0,31
15	0,3814	70 000	6,1	0,37
16	0,4132	30 000	6,4	0,5

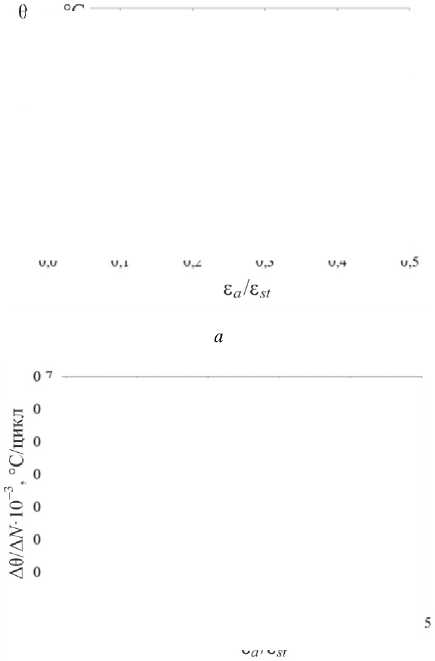
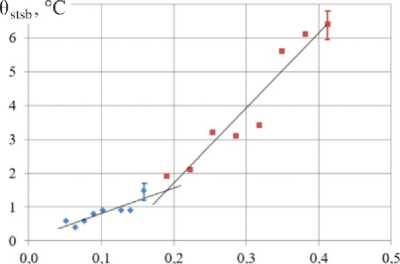
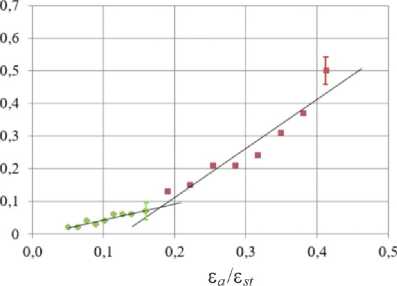
Рис. 7. Изменение осредненной по зоне А стабилизационной температуры θ stab ( а ) и Δθ/Δ N ( b ) для образца №1с ростом нагрузки в блоке

b

• Fig. 7.    Change in the stabilization temperature averaged over zone A θ stab ( a ) and Δθ/Δ N ( b ) for Sample 1with increasing load in the block

На рис. 7, а , приведена зависимость стабилизационной температуры, осредненной по зоне А, от амплитуды деформации ε a в блоке нагружения; показаны также доверительные интервалы для измеренных температур. Эта зависимость аппроксимируется двумя прямыми. Как описано выше, точка их пересечения соответствует пределу выносливости. В таблице для образца №1 приведены значения коэффициентов линейной аппроксимации для левой и правой ветвей аппроксимации

0 sab = ^k 1 ^S a / 6 st + ^Ь 1 и 0 sab = k 2 6 a / ⁶ st + ^b 2 , (1)

а также суммарное значение R ² Σ для обеих ветвей.

Соответствующие значения амплитуды деформации ε a * приведены в табл. 3. Аналогичные данные для скорости нарастания температуры в блоке нагружения Δθ/Δ N приведены на рис. 7, b , и табл. 2 и 3.

В табл. 3 приведены средние по двум испытанным образцам значения предела выносливости ε a *. Расхождение между исследованными образцами по коэффициенту вариации лежит в пределах 6 %. Расхождение между значениями ε a * , полученными по θ stab и по Δθ/Δ N , составило 6 %.

Для верификации полученных результатов были проведены стандартные усталостные испытания 18 образцов из той же партии (см. рис. 1) на той же экспериментальной установке с той же схемой нагружения на базе 10⁷ циклов. Построена кривая усталости и определен предел выносливости. Полученные по разработанной ускоренной методике значения ε a * согласуются с результатами стандартных усталостных испытаний. Предел выносливости ε a * , определенный по Δθ/Δ N , выше полученного из стандартных испытаний на 8,1 %, а определенный по θ stab – на 14,9 %. Такое расхождение сопоставимо с погрешностью определения предела выносливости, полученным стандартным методом.

В случае использования в качестве параметра нагрева величины Δθ/Δ N рассеяние экспериментальных значений вокруг аппроксимации по суммарному коэффициенту детерминации R ² Σ несколько меньше, чем в случае использования стабилизационной температуры θ stab , что свидетельствует о более высокой точности аппроксимации и определения предела выносливости.

Таблица 2

Коэффициенты аппроксимации зависимостей θ stab (ε a ) и Δθ/Δ N (ε a ) для образца №1

Table 2

Approximation Coefficients of dependencies θ stab (ε a ) and Δθ/Δ N (ε a ) for Sample 1

θ stab (ε a )					Δθ/Δ N (ε a )
k 1	b 1	k 2	b 2	R 2Σ	k 1	b 1	k 2	b 2	R 2Σ
7,5432	0,0638	22,1	-2,6976	1,689	0,4933	-0,0061	1,5058	-0,1896	1,799

Таблица 3

Полученные значения предела выносливости

Table 3

The obtained values of the fatigue limit

Параметр	ε a * /ε st среднее значение	Коэффициент вариации, %	Расхождение со стандартными усталостными испытаниями
θ stab	0,174	5,7	8,1
Δθ/Δ N	0,185	3,8	14,9
Стандартные усталостные испытания	0,161	–	–

Алгоритм определения предела выносливости элементов конструкции из ПКМ по разработанной методике можно описать следующим образом. На первом этапе проводятся предварительные испытания с целью анализа теплового состояния исследуемого образца на разных этапах усталостного разрушения, выявляются характерные зоны саморазогрева. Следующий этап исследования представляет собой непосредственно испытания с блочным циклическим нагружением. Для каждого уровня нагрузки определяются стабилизационная температура и скорость роста температуры в начале блока нагружения. На заключительном этапе проводит- ся обработка полученных результатов и определяется предел выносливости.

Разработанная методика может быть рекомендована для экспериментальной экспресс-оценки усталостной прочности элементов композитных конструкций на этапе прочностной доводки при выборе вариантов конструктивных и технологических решений.

Заключение

В рамках метода инфракрасной термографии разработана методика экспресс-оценки предела выносливости типовых элементов композитных конструкций на примере фланцев из слоистого углепластика. Методика предполагает блочное циклическое нагружение образца, вырезанного из натурной детали, с регистрацией температуры в выделенной зоне на его поверхности.

Сравнивались два варианта методики: с использованием стабилизационного значения повышения температуры в конце блока нагружения θ stab и с использованием скорости повышения температуры в начале блока