Эквивалентная схемная и математическая модели учёта геометрической неоднородности поверхности СВЧ многослойных интегральных схем на основе технологии низкотемпературной совместно-обжигаемой керамики

Z

rough

= 7

smooth

P rought

P smooth

= 7. , - К smooth ,

где K – поправочный коэффициент учёта геометрической неоднородности поверхности.

Проведённые авторами экспериментальные исследования неоднородности поверхности отечественных образцов сверхвысокочастотных (СВЧ) многослойных интегральных схем (МИС) на основе низкотемпературной совместно-обжигаемой керамики (НТК) методом сканирующей электронной микроскопии показали наличие неоднородности, отличной от не-

а                                   б

Рис. 1. Микрофотографии поверхности керамики DuPont Green Tape 951 (увеличение в 2700 раз) ( а ) и поверхности проводника из серебряной пасты 6148 Ag (увеличение в 2300 раз) ( б )

однородности поверхности печатных плат, рассмотренных ранее (рис. 1) [3, 4]. Полученные результаты дают возможность утверждать, что имеющиеся математические модели не позволяют описать неоднородность поверхности СВЧ МИС НТК и требуется разработка адекватной математической модели и численного метода.

Эквивалентная схемная модель

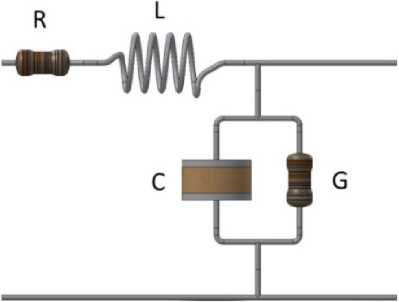
Самым распространенным элементом СВЧ МИС является микрополосковая линия передачи. Для эквивалентного представления такой линии передачи используют её схемную RLCG -модель (рис. 2) [5].

Однако в таком виде модель линии отражает только характеристики электрически коротких линий передачи, поскольку в ней невозможны процессы отражения и протекания электрического сигнала. Также в данной модели не учитывается сопротивление и индуктивность опорной линии, которые тоже влияют на характеристики линии передачи.

Данная модель работоспособна, если линия передачи по отношению к длине волны сигнала электрически короткая. Электрически короткими линиями в случае передачи синусоидального сигнала считаются линии, если её физическая длина l много меньше четверти минимальной длины электромагнитной волны A min разрабатываемого устройства. A min для линии передачи можно рассчитать следующим образом:

^•min = ^/ f max , (2)

где v – скорость распространения электромагнитной волны в линии передачи, м/с; f max – максимальная частота разрабатываемого устройства, Гц.

Электрически короткими линиями для цифровых схем, в которых передача сигнала выполняется прямоугольными импульсами, считается линия передачи, физическая длина которой много меньше длины переднего фронта сигнала.

Для учёта электрически длинных линий передачи используется метод деления длинной линии передачи на более короткие звенья (рис. 3).

GND

Рис. 2. RLCG -модель электрически короткой линии передачи

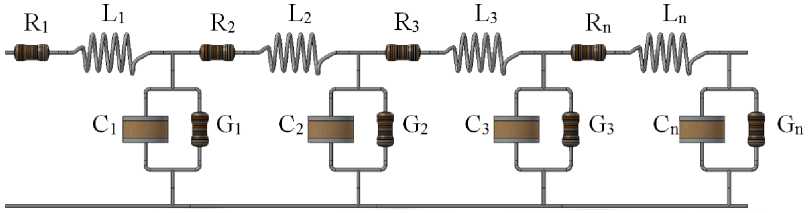
Рис. 3. Типовая схемная RLCG -модель электрически длинной линии передачи

И теперь, если учесть недостаток обычной RLC G-модели и подставить в неё индуктивность и сопротивление опорной цепи, получим эквивалентную модель электрически длинной линии передачи (рис. 4).

Построим эквивалентную схемную модель одного звена RLCG -модели линии передачи, позволяющей соединять RLCG -цепочки между собой, а также учитывающую RL -характеристики опорного слоя ( REF ). Для дальнейшего различия обычной и модифицированной эквивалентной схемной модели линии передачи введено обозначение четырёхсторонней RLCG -модели (рис. 5).

Полученная эквивалентная схемная RLCG -модель микрополосковой линии передачи (рис. 5) позволяет моделировать неоднородность поверхности любой формы, поскольку появляется возможность имитировать линию передачи любым количеством цепей и звеньев. В местах, где на пути цепочки встречается паз размером меньше, чем звено цепи, вместо разрыва в цепочки будем рассчитывать RLCG -характеристики звена с использованием коэффициентов коррекции согласно разработанной математической модели (21) – (24).

Согласно предлагаемому методу линия передачи имитируется последовательностью схемных RLCG- компонентов со связями между линиями в виде RL -последовательности. Линия обладает индуктивностью ( L ) , активным сопротивлением ( R ) , межпроводной ёмкостью ( C ) и проводимостью утечки через изоляцию ( G ).

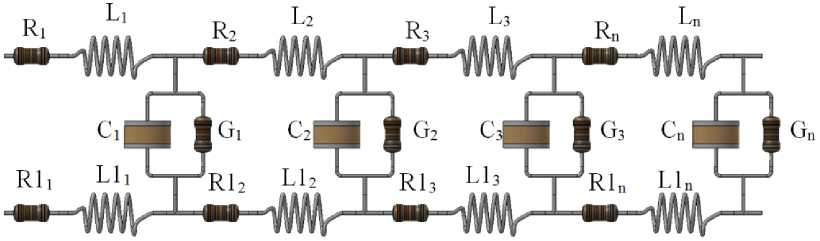
Рис. 4. Улучшенная схемная RLCG -модель электрически длинной линии передачи

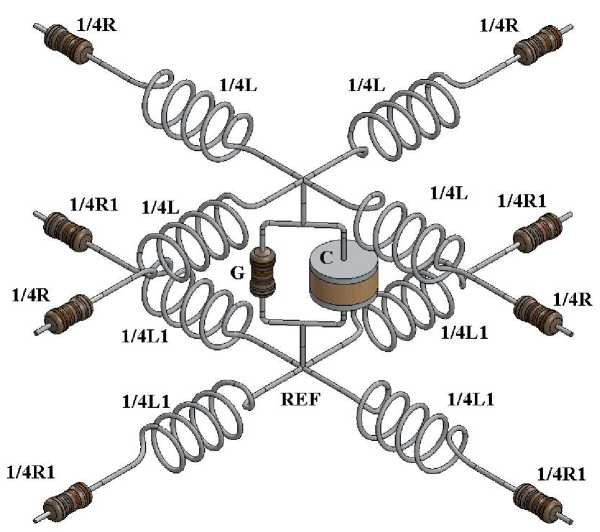
Рис. 5. Четырёхсторонняя схемная RLCG -модель микрополосковой линии передачи

Данный метод имитации линии передачи является универсальным и легко интегрируется в различные расчётные системы схемотехнического моделирования [6, 7]. Так же будет действовать правило: чем больше цепей и звеньев, тем точнее имитация неоднородности поверхности.

В качестве примера на рис. 6 представлена схемная модель микрополосковой линии передачи, в центре поверхности которой находится паз.

Математическая модель

При разработке математической модели линии передачи СВЧ МИС НТК необходимо учитывать, что в связи с поверхностным эффектом ток будет огибать поры не вертикально, как в модели Хэммерстада, а горизонтально по поверхности проводника.

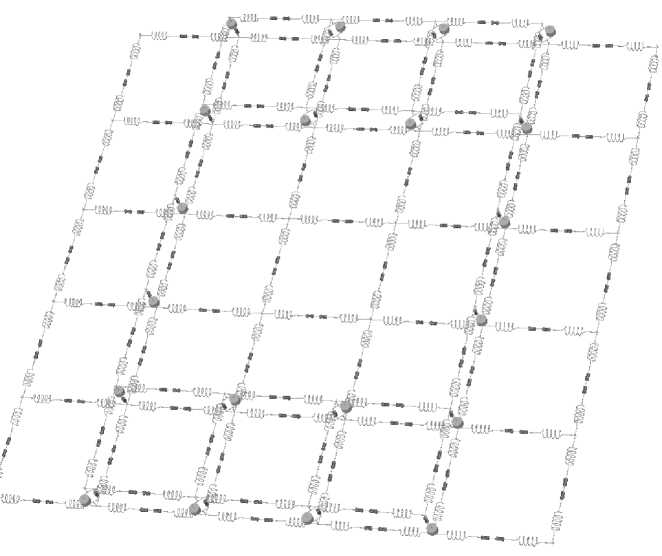
Рис. 6. Пример эквивалентной схемной RLCG -модели микрополосковой линии передачи СВЧ МИС НТК с учётом геометрической неоднородности её поверхности

Полученные ранее результаты позволяют сделать вывод о том, что для имитации неоднородности поверхности СВЧ МИС НТК необходимо построить модель, учитывающую форму контуров впадин, которая может представлять собой коэффициенты корректировки длины и ширины линии передачи при вычислении значений её RLCG -параметров.

Поскольку впадины снижают площадь распространения сигнала, значит, реальная ширина линии передачи должна снизиться. Вычислим коэффициент коррекции ширины:

K

w

= 1 -

P rought

w ■ d

Так как на пути распространения тока возникают впадины, то ток будет огибать их и реальная длина распространения тока увеличится, коэффициент корректировки длины линии передачи будет вычисляться следующим образом:

P

K = i + -oughN ^d w • d

.

Вычислим значения RLCG -параметров.

Постоянные распространения и волновое сопротивление для линии передачи можно найти по выражениям:

у(П = «(П+.М(П,

где

7 = Lc

--—--ln

^•^eff

I

^•a(w/h) w

+ J1+4^J

[ /30 666^\ 0,75281

I w J J *                             ⁽⁷⁾

η 0 – импеданс воздуха; ε eff – эффективная диэлектрическая проницаемость.

Подставив в выражения (6) и (7) значение w , умноженное на соответствующий ей коэффициент коррекции, получим выражение для расчёта волнового сопротивления с учётом геометрической неоднородности поверхности:

где

_{Z c} =

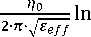
г

h*a( w /h) p^T

4-(h) ²

-■ ■■   -■ 2- 6 ■-■■    ./

Согласно [8] обозначив скорость света c, найдем постоянную распространения с учётом потерь для конкретной частоты в соответствии со следующим выражением:

y⁽D = а_с(Л + а_а(Л ■j^T^rCD.

c

где

Потери в металлическом проводнике и диэлектрические определяются так:

а^-гзЦг+^+^^У^ ^Weff     Л t Ыс(П

a_c(f) = 27,3 -^--

E _T - 1

^E eff ¹

^^E e f f

tan(5)

2Л/ , C

R s (T) = ^^ • ^ ^ • P ^ ^f,

l

₃₂₊(^^) ² ’

1,25      , /2h\l         w - K_w    1

W^ w       п^],если — —,

1,25           4nw - K _w           w - K _w    1

^W" ^w n             t ’ ли h - ²n '

Зная уравнения Z c и y ( f ), можно получить значения элементов, зависящих от длины для эквивалентной RLCG -схемы линии передачи. Для этого будем использовать уравнения, связывающие Z c и y с RLCG -пар аметрами [9].

У = ^⁽R yjtoLXG +jtoC), (15)

^Zc j G+V^C •                                                          ⁽¹⁶⁾

Далее, решая выражения (15) и (16), выведем уравнения для определения значений элементов RLCG -схемы:

R = Re{yZ_c},

_T _ Im{yZj ь —------ ,

to

C — Im f—] to, zc

G = Re K],

Zc где Re[z] и Im[z] – реальная и мнимая части комплексного числа z и ω = 2πf – угловая частота. После чего, обозначив ρ как проводимость материала, установив значение длины линии передачи d с учётом коэффициента коррекции (3) и используя выражения (8), (10), (17) – (20), можно получить выражения для расчёта значений RLCG-линии передачи:

R =

d - KdV^wf w ^ K_w

, _ a ^ ^K _d ^ Z c

^L = -- c--

„ _ d - K dV f ^TJ c ^ Z_c ^,

G= d-Кд- tan(5) • to • C, где d – длина линии передачи; μ 0 – магнитная проницаемость вакуума; tan(δ) – тангенс угла диэлектрических потерь.

Заключение

Таким образом, в ходе исследования разработана:

– эквивалентная схемная RLCG -модель микрополосковой линии передачи СВЧ МИС НТК, позволяющая осуществлять дискретизацию её поверхности с анизотропной проводимостью и повысить скорость расчёта параметров полезного сигнала при сохранении требуемой точности, предъявляемой к схемотехническому и топологическому проектированию;

– математическая модель микрополосковой линии передачи СВЧ МИС НТК, отличающаяся от существующих тем, что посредством коэффициентов коррекции длины и ширины имеет возможность учитывать геометрическую неоднородность её поверхности и позволяет повысить точность расчёта параметров полезного сигнала.