Электрический ветер в системе электродов игла-решетка

Явление электрического ветра, возникающее в коронном разряде, используется в ряде технологических устройств сельскохозяйственного производства [1–3]. На изучение электрического ветра были направлены усилия многих ученых, но, несмотря на это, литературные данные по этой проблеме весьма ограничены и не всегда надежны. Электрический ветер изучался в основном в разрядном промежутке электрофильтров с целью выяснения его влияния на перемещения частиц пыли. При этом в принимаемых допущениях были существенные разногласия. Так, в работе [1] напряженность электрического поля на коронирующем электроде принимается равной нулю [Ео (х « 0) = 0], а в работе [2] напряженность на коронирующем электро- де принимается равной напряженности зажигания короны, т.е. Ео = Е

В первом случае было получено выражение для определения напряженности на приемном электроде:

E l = [ ( Э / и ) ² + ( 2 j / 8 -и ) • L ] 12 - ( Э / и ) , (1) где Е L – напряженность на приемном электроде – сетке, кВ;

Э - скорость электрического ветра за приемным электродом, м/с;

и - подвижность ионов, м²/св;

j – плотность тока, А/м²;

8  - диэлектрическая проницаемость воздуха, А·с/в·м;

L – межэлектродное расстояние, м.

А также выражение для определения скорости электрического ветра:

Э =

где р - плотность воздуха, кг/м³.

j • L

] и ■ р • (1 + (28 / р U22 )У2

j - L

Р •и(1 + V)

Расхождение теоретических значений скорости с экспериментальными значениями не превышает 4%.

Во втором случае было получено вы-

E L

. и+

j • ^x 1

8 U J

Э 2и

При этом выражение для определения

скорости электрического ветра имеет вид:

ражение для определения напряженности

на приемном электроде:

Э =

3 • J • f ( x )

\ п ■ р ■ и • x

где J – ток разряда, μА;

f (x ) = (a ■ xj- [(1 + u- x )-(1 + c ■ x )2 J, a = 3,64·104·L, см; υ =1,4·102·L, см; c =70^L2, см2; x{ = x/L ; x - расстояние от кончика иглы, см.

Экспериментальная проверка, проведенная авторами, показала, что расчетные значения скорости ветра на 15–20% меньше экспериментальных.

В работе [3] также получено уравнение для определения скорости электрического ветра на основе перепада давлений во внешней области разряда:

2 j ■ L

\ p ■ ^{u -(} 1 + £ ) ,

где £ - коэффициент потерь.

При коэффициенте потерь, равном единице ( ^ = 1 ) , уравнение (5) принимает

Экспериментальная проверка уравнения (6) показала, что расчетные значения больше экспериментальных на 3–6%, что приемлемо для инженерных расчетов. Однако в этом уравнении нет обоснования равенства коэффициента потерь единице, т.е. £ = 1.

В связи с этим нами была предпринята попытка получить выражение для определения скорости электрического ветра за пределами разрядного промежутка. Предположим, что давление, создаваемое потоком электрического ветра в плоскости приемного электрода – сетки, равно:

p - 9 ² = S o • s • E L , (7) где s =8,85^10^-12 А^с/в-м - диэлектрическая проницаемость среды.

Вместо ЕL подставим уравнение (3) и вид:

⁹ = 7( ^{j - L} W "^u ) •

решим его относительно скорости:

9 =

j • L

j • L

где у = ^{[ s} o ^{/ (} p • ^{u )J 12} •

Коэффициент ψ в уравнении (8) при p =1,29 кг/м3 и u =2,16-10—4 м2/(с^в) равен: ψ=1,78·10-4, т.е. им можно пренебречь. То- гда уравнение (8) примет вид:

9 =

При j =0,016

j • L

4 P"u н/м2, L=63·10-3

м ско-

рость ветра по (8) равна 9 =1,91 м/с, а по (9) 9 =1,913 м/с. Разница составляет 0,15%.

Иногда в практике исследуют графи- ческие зависимости скорости электрического ветра за пределами разрядного промежутка от напряжения на электродах разрядного промежутка.

К настоящему времени отсутствуют приемлемые выражения для определения скорости ветра от приложенного напряжения.

Рассмотрим этот вопрос при следующих допущениях:

• 1.    Электрическое поле Е, плотность тока j и скорость воздуха в области дей-

• ствия поля имеют только осевые составля-
• ющие.

• 2.    В межэлектродной области плотность тока и осевая составляющая скорости постоянны и одинаковы по поперечному сечению потока площади S .

• 3.    Объемная сила является результатом действия электрического поля на униполярные ионы, обладающие постоянной подвижностью υ .

Исходя из этих допущений, а также пренебрегая вязкостным членом для выделенного объема и одномерной системы, уравнение Навье-Стокса можно представить в следующем виде:

P-92 • S =JLk-Ps • ESdx.(10)

Уравнение Пуассона вдоль оси х имеет вид:

dEL _ Ps dx S    dEL 'S = ps ' dx(11)

Интегрируя (11), получаем

EL = (Ps - x)/S •

Подставляя (12) в (10) и интегрируя, получаем при x_K = 0:

p • 92 = P^ • L2.(13)

s

Из (12) при x = L получаем 9 = ( E_l ■ £ ) / L .

9 = P_e ■ L •

1     U	1
\/ P ■ £    L £	P ■ £

U £

LilP ’ откуда

где U – напряжение на электродах разрядного промежутка.

Из уравнений (15) и (9) можно найти зависимость напряжения на электродах от длины разрядного промежутка L и плотности тока j . При равенстве левых частей

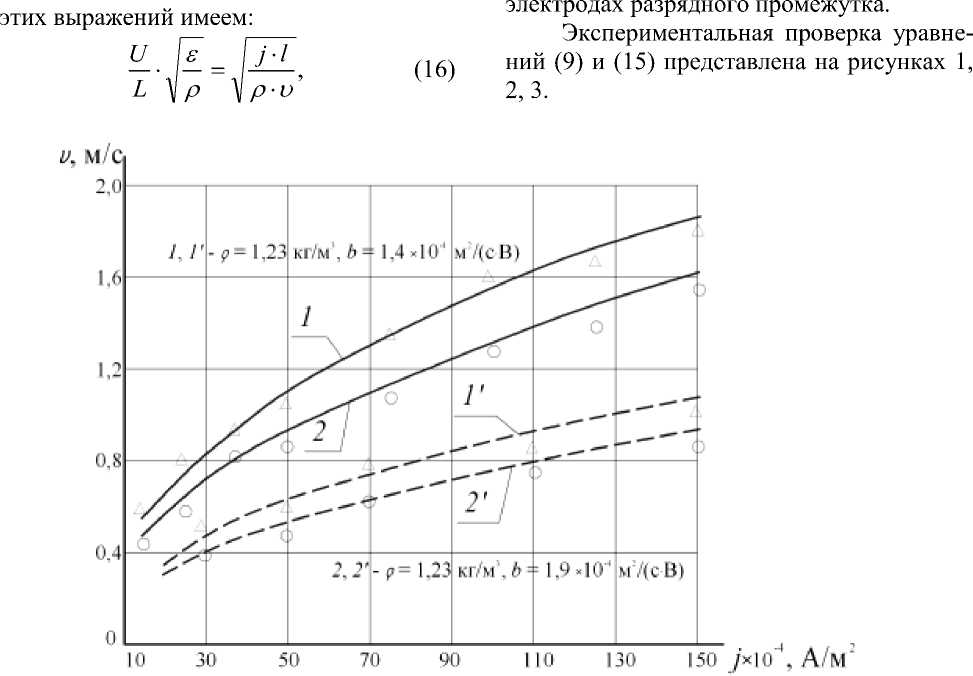
Рис. 1. Графические зависимости скорости электрического ветра от плотности тока для отрицательной и положительной короны:

1, 1′, – теоретические зависимости для положительной короны;

2, 2′ – теоретические зависимости для отрицательной короны;

1′, 2′ – для межэлектродного расстояния L=16·10-3 м;

1, 2 – для межэлектродного расстояния L = 5·10-2 м;

∆ – эксперимент для положительной короны;

◦ – эксперимент для отрицательной короны

Теоретические зависимости построены по аналитическому уравнению (9) Погрешность с экспериментом не превышает 4–6%.

На рисунке 2 представлены графические зависимости скорости электрического

Из (13) с учетом (14) получаем уравнение для скорости

U = L •   j^l-

•

£ • U

Задаваясь длиной разрядного промежутка L и плотностью тока j , по выражению (17) определяем напряжение U на ветра от напряжения на электродах разрядного промежутка. Теоретические графические зависимости построены по выражению (15) для L=6·10-2 м и L=3·10-2 м для отрицательной короны.

U,кВ

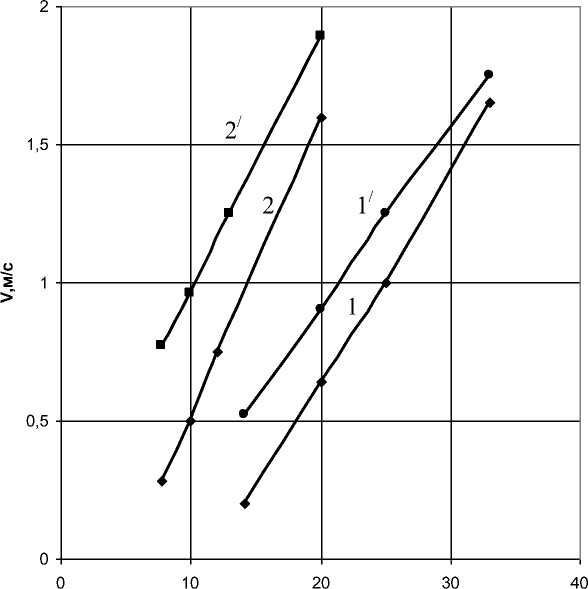
Рис. 2. Графические зависимости скорости электрического ветра от напряжения на электродах разрядного промежутка для отрицательных корон:

1, 2 – экспериментальные зависимости (L = 6,0 см и L = 3,0 см соответственно); 1′, 2′, – теоретические зависимости

На рисунке 3 представлена графическая зависимость скорости электрического ветра от напряжения на электродах раз- рядного промежутка для положительной короны (L=2,0 см).

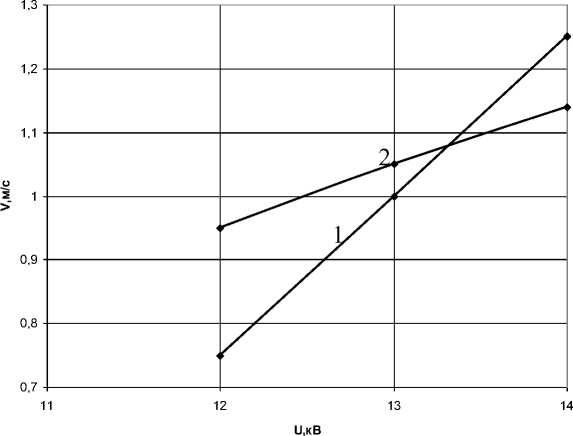
Рис. 3. Графическая зависимость скорости электрического ветра от напряжения на электродах разрядного промежутка:

1 – экспериментальная зависимость; 2 – теоретическая зависимость

Анализ этих зависимостей показывает, что погрешность аппроксимации для отрицательной короны колеблется от 50% в начале разряда (U=8 – 12 кВ для L=3,0 см и U= 15 – 20 кВ для L=6,0 см) до 6–11% при дальнейшем повышении напряжения.

Для положительной короны погрешность колеблется от 26% в начале разряда (12–12,5 кВ) до 4–11% при дальнейшем повышении напряжения.

Таким образом, полученное уравнение (15) не совсем адекватно описывает зависимость электрического ветра от напряжения на электродах разрядного промежутка.

В связи с этим нами была предпринята попытка получить эмпирические зависи- мости по экспериментальным данным как для отрицательной, так и для положительной короны.

Эти зависимости были определены для наиболее распространённых длин разрядного промежутка L=20, 30, 60 мм (рис. 4, 5).

Для отрицательной короны L=30,0 мм (рис. 4).

ϑ=0,2109·U-0,6016,   R2=0,998.(18)

Для отрицательной короны L=60,0 мм (рис. 4).

ϑ=0,0615·U-0,5674, R2=0,996.(19)

Для положительной короны L=20,0 мм (рис. 5).

ϑ=0,2543·U-2,3, R2=0, 997.(20)

Радиус закругления острия r = 0,05 мм.

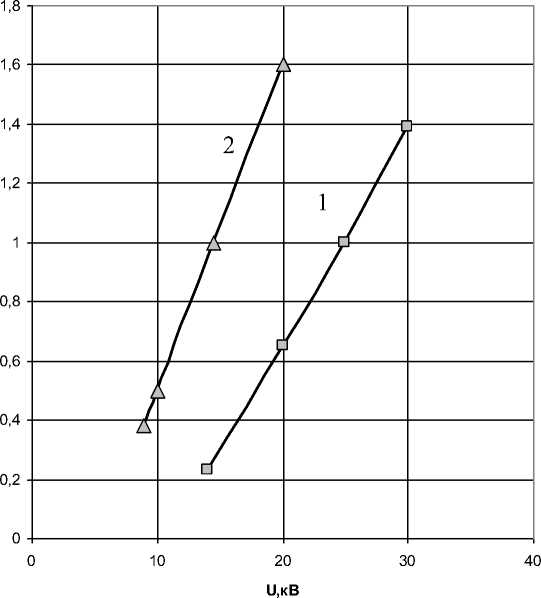
Рис. 4. Графические зависимости скорости электрического ветра от напряжения на электродах для отрицательной короны:

1, 2 –эмпирические зависимости (L = 6,0 см и L = 3,0 см соответственно);

Δ, □, – экспериментальные значения

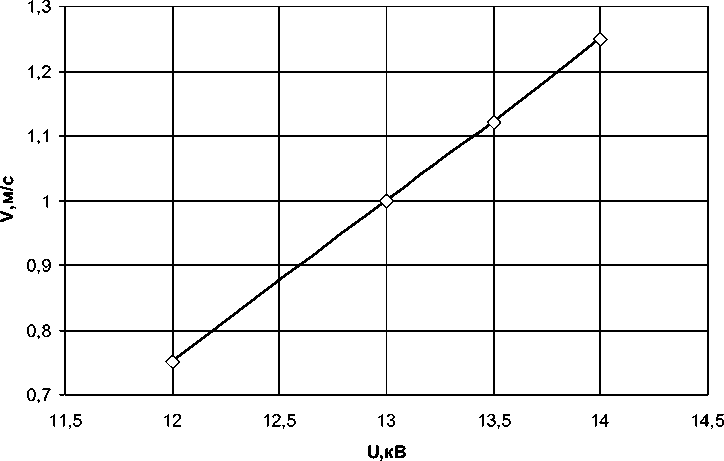
Рис. 5. Графические зависимости скорости электрического ветра от напряжения на электродах для положительной короны L = 2,0 см - – эмпирическая зависимость; о – экспериментальные значения

Таким образом, получены аналитические и эмпирические зависимости, позволяющие определять скорость электрического ветра от плотности тока и напряже- ния на электродах разрядного промежутка игла – сетка с приемлемой для практики погрешностью, не превышающей 6%, что приемлемо для практических расчетов.