Электродинамическая модель оценки электромагнитной безопасности поля излучения конического рупора

Основой решения задач электромагнитной (ЭМ) экологии является разработка универсальных подходов к расчету полей в зонах, прилегающих к излучающему объекту. В числе первых значимых работ этого направления следует назвать [1-3]. Проблемы ЭМ-экологии в систематическом виде впервые были сформулированы в [4-5].

Излучение ЭМ-полей коническими рупорами рассматривались многими авторами, например [6-10]. Анализ результатов этих работ показал, что для их применения в моделях прогнозирования ЭМ-обстановки необходимы дополнительные исследования по расчету коэффициента направленного действия (КНД) в зоне Френеля с учетом расфазировки апертуры рупора.

Методика расчета

Ключевым моментом при решении задач оценки ЭМ-безопасности является расчет плотности потока энергии (ППЭ) ЭМ-излучения. В свою очередь, расчет ППЭ требует предварительных вычислений двух параметров излучателя – нормированной характеристики направленности и КНД. Ниже приводится подробное изложение методики расчета этих параметров и ППЭ кони- ческого рупора с прямолинейной образующей, показанного на рис. 1.

Геометрию рупора зададим параметрами: a – радиус апертуры (раскрыва); l – длина рупора. В большинстве случаев конический рупор возбуждается круглым волноводом с волной типа H ₁₁. Примем, что плоскости H соответствует угол φ = 0, а плоскости E – угол φ = π⁄2.

Для зоны Френеля, представляющей особый интерес при оценке электромагнитной безопасности конического рупора, поле в точке наблюдения может быть представлено в виде [11-12]:

где т) = 2л 1

О О

Функция, аппроксимирующая распределение амплитуд в плоскости раскрыва рупора при его возбуждении волной H ₁₁:

()

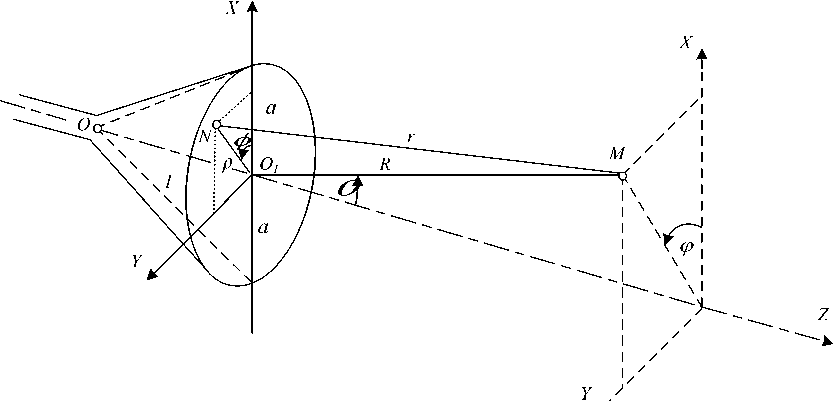
Рис. 1. К расчету плотности потока энергии поля, излучаемого коническим рупором

Обобщенный параметр

8 = ка sin 9 = ^ a sin 9.         (4)

Параметр, учитывающий результирующую расфазировку, у = ко?/21 + ka2/2R.         (5)

В (5) первое слагаемое (ко²/21) учитывает квадратичную расфазировку, возникающую из-за разности длин путей от точки O до текущей точки N(p, ф) в апертуре. Второе слагаемое ка²/2R учитывает квадратичную расфазировку, связанную с разностью хода от центра апертуры O ₁ и точки в апертуре N(p, Ф) до точки наблюдения M(R,ey

Современные ЭВМ позволяют выполнить интегрирование согласно (2), не прибегая к результатам предварительного аналитического сведения интеграла к рядам функций Ломмеля 1-го и 2-го порядка [9-11].

Результаты расчетов

На рис. 2 приведены нормированные диаграммы направленности (ДН) рупора для плоскости YOZ ( E -плоскость, φ = π ⁄2 ). Расчет выполнен по формулам (2)-(5), аргументом является обобщенная координата 8 = ка sin 9 при фиксированных значениях квадратичной расфазировки γ в интервале от π до 6 π .

Аналогичные ДН получены и для плоскости XOZ (H-плоскость, φ=0). Эти ДН в статье не приведены – это объясняется тем, что значение ширины ДН по уровню половинной мощности в Е-плоскости у конического рупора больше, чем в H-плоскости. Поэтому для оценки ЭМ-безопас- ности излучения конического рупора достаточно использовать ДН, соответствующие плоскости φ = π⁄2. Эти ДН можно принять в качестве гарантированных огибающих для ДН в любой другой плоскости, когда φ ≠ π⁄2.

Учитывая, что ДН построены в зависимости от обобщенной координаты δ и большого диапазона значений расфазировки (от γ = π до γ = 6 π ), можно говорить об их универсальности для реальных типоразмеров конического рупора.

Формула для расчета ППЭ конического рупора имеет вид [2]:

П_кр = (Р/4л19²Жг)Р²(8,у),Вт/м\ (6)

где P – мощность, излучаемая антенной, Вт; R – расстояние от центра апертуры рупора до точки наблюдения M ( R ,θ), м; D ( γ ) – КНД расфазирован-ного рупора в направлении θ , заданном обобщенным параметром δ = ка sin 9; F²(8,y) – нормированная характеристика направленности рупора по мощности.

Если в (6) перейти от размерности Вт/м2 к мкВт/см2, то выражение для Πкр приводится к виду

П_кр = 100(P/4nR²)D(y)F²(8,y), мкВт/см². (7)

Для получения расчетного выражения D ( γ ) воспользуемся имеющимся в [11] графиком изменения КНД расфазированного конического рупора (для главного направления излучения θ = 0), возбужденного волной H ₁₁, по отношению к КНД синфазно возбужденной апертуры. График представлен в виде функции суммарной расфазировки на краю апертуры, то есть

Х(у) = D(y)- 0(0), дБ. (8)

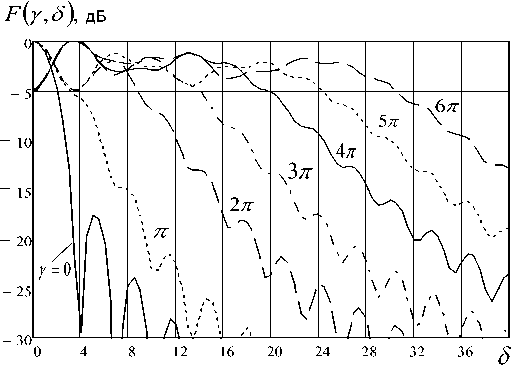
Рис. 2. Влияние расфазировки на ДН конического рупора в Е-плоскости (<р = тг/2)

Для синфазно возбужденной волной H ₁₁ апертуры конического рупора значение КНД определяется как

5(0) = 0,84(4тг2а2/22).          (9)

При переходе к децибелам имеем

5(0) = - 0,757 + 201og (2яа/Л), дБ. (10)

Для рупоров, имеющих значения суммарной расфазировки γ , равные 2 n π, n = 1; 2; 3… , функция (8) имеет частные минимумы, а при γ = (2 n +1) π – максимумы. Для оценки ЭМ-безопасности целесообразно воспользоваться значениями χ ( γ ), соответствующими огибающей максимумов (см. рис. 3) этой функции, которая аппроксимируется полиномом третьей степени [10]:

Х(у) — 1,34 10 3у3 — -4,34 10“3у2 - 1,46у, дБ.

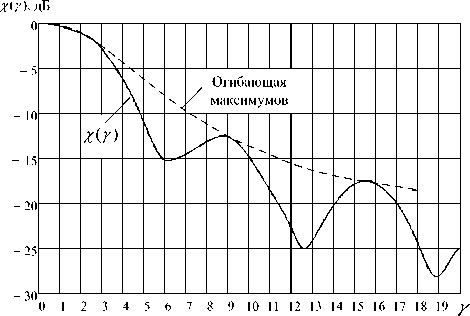
Рис. 3. Изменение КНД расфазированного рупора

С учетом изложенного, выражение для огибающей КНД в функции суммарной расфазировки принимает вид:

5(у) = 20 log(2mi//l) — 0,757 + /(у), дБ. (12)

Для удобства практических расчетов можно от абсолютных значений величины ППЭ перейти к относительным: децибелам относительно 1 мкВт/см2. Тогда выражение (7) с учетом (10) и (12) можно представить как

Пкр = 20 + 10 log(P/4^E2) дБ + 5(0)дБ +

+z(y) дБ + 5(5, у), дБ.                (13)

Значения огибающих КНД для расфазиро-ванного рупора рассчитаны по формуле (12). На рис. 4 приведены графики D ( γ ) конического рупора для различных значений радиуса его апертуры как функции расфазировки.

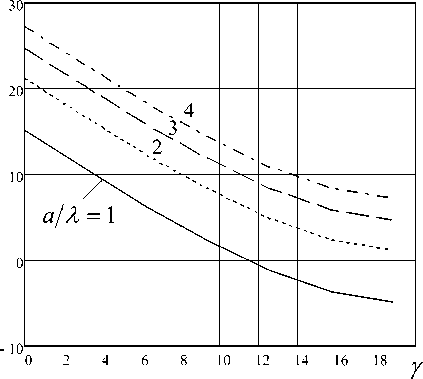
Рис. 4. КНД расфазированного конического рупора (гарантированные значения)

Расчет КНД конического рупора по методике, предложенной в [9], не учитывает фактор расфазировки апертуры, что приводит к существенному завышению расчетных значений КНД.

Пример расчета

Конический рупор, имеющий геометрические размеры (см. рис. 1) a = 15 см, L = 45 см возбуждается волной типа H ₁₁ на длине волны λ = 3 см. Подводимая мощность P = 100 Вт. Необходимо рассчитать ППЭ в точке M с координатами R = 1,5 м, в = 20°.

Результаты расчета: γ = 6,807 согласно (5); δ = 10,745 согласно (4); D ( γ )=19,469, дБ согласно (12). Значение нормированной характеристики направленности

F(5 = 0,745, у = 6,807)=-5,422 дБ.

Нормированная ДН, рассчитанная с применением численного интегрирования по формулам (2-5), приведена на рис. 5. Значение ППЭ, дБ/мкВт = 39,5 согласно (13), что соответствует ППЭ = 8,982-Ю3 мкВт/см2.

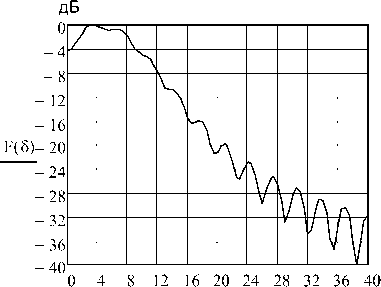
Рис. 5. Нормированная ДН конического рупора

Заключение

Поставленная задача уточнения математической модели для расчета значений ППЭ вблизи апертуры конического рупора решена. Предложенную методику расчета можно рекомендовать для включения в новую редакцию нормативных документов по определению ППЭ ЭМ-излучения в местах размещения радиосредств соответствующего диапазона.