Электродинамические параметры коаксиального кабеля при распространении биполярных импульсов

Передача биполярных импульсных сигналов по коаксиальному кабелю является одной из характерных особенностей технологии 10Мбит Ethernet и ее модификаций, таких как 10BASE5 и 10BASE2 [1, 2], достаточно еще распространенных в телекоммуникационных локальных вычислительных сетях (ЛВС) стандарта IEEE 802.3. В этих технологиях передача импульсных сигналов по коаксиальному моноканалу многопользовательского сетевого взаимодействия осуществляется манчестерским кодом при номинальной длительности tp тактового интервала, равного 0,1 мкс, а многостанционность доступа к среде пакетной передачи – протоколом CSMA/CD1. В качестве моноканала для модификации 10BASE5 используют так называемый толстый кабель типа RG-8/U, 0,375 дюймовый (9,5 мм) с пористым наполнителем и малыми диэлектрическими потерями либо кабель RG11, в котором потери электромагнитной мощности сигналов также могут быть отнесены только к электрическим потерям на проводящих поверхностях сегмента кабеля при его длине, не превышающей 500 м. При той же технологии пакетной передачи альтернативным моноканалом является «тонкий» коаксиальный кабель RG58 либо даже кабель РК-50, но при этом максимально допустимая длина сегмента оказывается ограниченной значениями 185-200 м из-за повышенного затухания и вносимых сегментом искажений в передаваемых импульсных сигналах.

Конструктивное исполнение толстого коаксиального кабеля относят к категории жесткого моноканала с ограничениями на его изгиб при монтаже в помещениях. Выполнение тех же работ с тонким коаксиальным кабелем значительно проще, что является преимуществом 10BASE2 по сравнению с иными моноканалами ЛВС [3, 4]. При других исполнениях кабельной среды ограничения по длине сегментов также зависят от геометрии их поперечного сечения, электрофизических свойств диэлектрика и глубины проникновения электромагнитного поля в приповерхностные слои направляющих проводящих поверхностей моноканала, что выражается зависимостями коэффициентов пространственного α c и временного затухания β c импульсных сигналов от их длительностей. Установление таких зависимостей во временной области их определения можно отнести к категории сложной [5], но разрешимой на современном уровне развития математического обеспечения и вычислительного моделирования задачи электродинамики, которая может допускать и ее нестрогое решение при вспомогательных допущениях, представленных в настоящей статье.

Характерные особенности процесса распространения импульсных сигналов по коаксиальному кабелю

В формате классической модели этого процесса пространственно-временные распределения E ( z , t )-, H ( z , t )-составляющих напряженностей электромагнитного поля и плотностей поверхностных токов δ _s ( z , t ) на направляющих проводящих поверхностях определены их структурой, схематически представленной для фиксированного момента времени t 1 на рис. 1.

Согласно модели этого процесса внутренний проводник радиусом r 1 характеризуется его знакопеременными потенциалами относительно нулевого потенциала внешнего проводника радиусом r ₂, обусловленными прохождением импульсного сигнала, которым создается пространственно-временное распределение плотности электрического заряда (на рис. 1 не показано) и распределение плотности δ ⁽ _s ¹⁾ поверхностного тока. При достаточно быстром изменении электрического поля в диэлектрике кабеля токами утечек можно пренебречь по сравнению с плотностью тока смещения, что позволяет использовать уравнение непрерывности в определении значений δ s ( z , t ) как продолжений векторного поля плотности тока смещения на границе раздела сред. В отличие от процесса распространения одиночных импульсов или сигналов, передаваемых посредством несущего гармонического электромагнитного колебания, при передаче биполярных импульсов плотности δ s ( z , t ) поверхностных токов проводимости почти следуют переходным состояниям плотности тока смещения, а для приповерхностных слоев проводящей среды характерна гораздо бóльшая инерционность, обусловленная процессом проникновения электромагнитного поля в эти слои. Другими словами, начальные и граничные условия при каждом реверсе электромагнитного поля должны выполняться здесь для двух процессов, первый из которых характеризуется распространением – 27 –

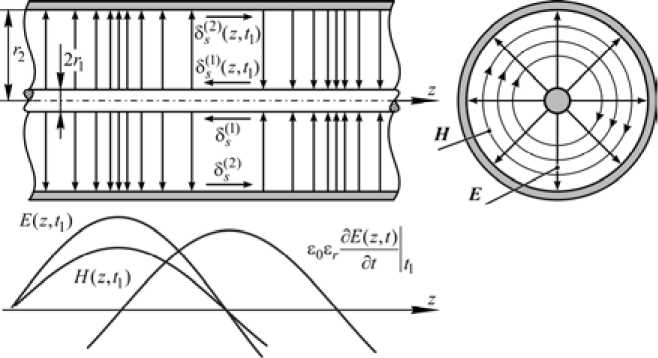
Рис. 1. Пространственно-временные распределения составляющих напряженностей электромагнитного поля и поверхностных плотностей токов на проводящих направляющих поверхностях коаксиального кабеля

Fig. 1. Spatial-time distributions of electromagnetic field components and surface current densities on the conductive guide surfaces of the coaxial cable

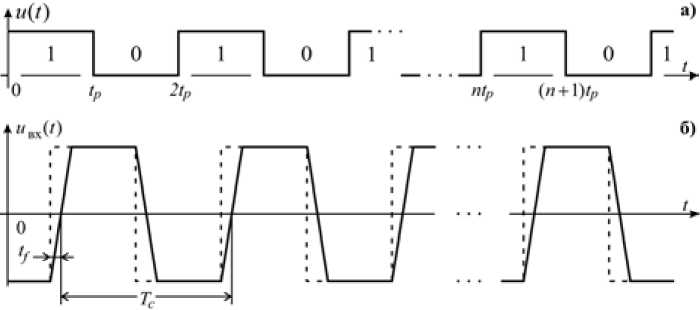
Рис. 2. Временные диаграммы импульсных сигналов: а – для фрагмента исходной двоичной б

– для соответствующих биполярных импульсов на входе коаксиального кабеля

Fig. 2. Waveform diagrams of pulse signals: a – for the reference binary sequence fragment; б – for the corresponding bipolar pulses at the coaxial cable input биполярных импульсов по диэлектрику кабеля, а второй – проникновением электромагнитного поля в его проводящие поверхности. При этом начало каждого передаваемого пакета содержит 64-битное поле, инициируемое исходной двоичной последовательностью, фрагмент которой представлен на временной диаграмме (рис. 2а) идеализированными прямоугольными импульсами u(t), а соответствующие этому фрагменту биполярные импульсные сигналы uвх(t) на входе коаксиального кабеля – двумя временными диаграммами (рис. 2б), первая из которых выделена пунктирными линиями, в идеализации сигналов манчестерского кода, а вторая – сплошными линиями, с учетом ненулевых длительностей tf фронтов этих биполярных сигналов.

Принимая во внимание периодичность u _вх( t ) в пределах пакетного поля синхронизации, представим эту зависимость ее разложением в ряд Фурье

и вх( t ) =

4 U

( , V        sn (3 “0 tf) ■ , sin(©otf )sinmot +-----sin3mot +

sin ( 5 to o t f ) ,

⁺     25    sin⁵ m o t + к +

sin ( k to o t f ) k ²

sin k to 0 t + K ,

где » о ^ t p , 0 < . <  2 . , = T c .

Выбор пакетного поля синхронизации для оценок допустимых значений электродинамических параметров обусловлен тем, что наибольшая ширина спектра, минимально необходимая для передачи цифровых данных по коаксиальному кабелю, относится именно к этому режиму при прочих равных условиях. В периодической последовательности биполярных импульсов длительности их фронтов могут относиться к интервалу 0 <  t f <  t p / 2, и если эти длительности задать целыми долями периода T_c = 2 t_p , то структура ряда (1) останется регулярной. Это условие не является принципиальным, но позволяет упростить необходимые в последующем анализе расчеты. В частности, при t f = t p / 2 ряд (1) записывается в виде

16 U u вх ( t ) =

sinro01 + -sin3ro01 —— sin5ro01 —— sin7ro01 +, 9          25          49            _ для которого характерно попарное чередование знаков гармонических составляющих в их блоках по четыре слагаемых (для 1-го блока здесь положительны 1-я и 3-я гармоники, а для 2-го блока 9-я и 11-я гармоники, причем 5, 7, 13 и 15-я гармоники ряда отрицательны).

Поверхностные плотности токов проводимости здесь тоже периодичны и формально определены скоростью изменения нормальной составляющей плотности Dn(z, t) = £о£rEn(z, t) потока электрического поля на проводящих поверхностях коаксиального кабеля в виде dVr,                z^z 8                 ,

₅ , ^{( z,t} V-- [ ^f . ( t -- M D n ( ^{z , t} ) ]=-u D n ^{( z}, t )» f - ( ^{1 - z} “ ) + f ■ * t- zf ")!, D n ^{( z,t} ) *    (3)

" f'l2)( '-->)f2 (1), где f1(1,2) – дважды дифференцируемые неявные функции профилей δS(1,2), удовлетворяющих граничным условиям для последовательных фиксированных моментов времени; f2(t) – функция мгновенных значений δS(1,2), определенная нормированием ряда (2) к уровню биполярного импульса для фиксированных значений z, f2 (t ) = 162^0

cos to g t + ^cos3 ® о t - ~cos5 ® о t — ~cos7 ® о t +

При допущении (3) относительно структуры пространственно-временного распределения значений 5$^1,2^(z, t) далее для упрощения записи в качестве независимой переменной функций f1(1,2) будет указываться только (z/υ) – аргумент: на поверхности внутреннего проводника как функция профиля f1(1)(z/υ), а на поверхности внешнего проводника – f1(2)(z/υ), которые отличаются по уровню их интенсивности при единой f2(t). В этой модели описания особен-– 29 – ностей процесса распространения импульсных сигналов значениями 5$1,2)(z, t) представлены их пространственно-временные характеристики, которые определены только на взаимосвязанных последовательностях (t, z/υ) – аргументов произведением функций (3), применительно к граничным условиям электродинамических состояний внутреннего и внешнего проводников коаксиального кабеля.

Анализ электродинамического состояния внутреннего проводника коаксиального кабеля

Математической моделью процесса проникновения электромагнитного поля биполярных импульсов в приповерхностные слои этого проводника являются уравнения Максвелла rot H =^c 1E ;

⁶ H rot E =- ^0 — , 6 1

которые можно переписать относительно плотности 8 = e z 8 _z ( r , t ) = e z о ci E z ( r , t ) тока проводимости в виде

rot H =8 ;    rot 8=-c с 1 ц 0     .

5 t

Применяя к системе уравнений (5) стандартное преобразование, получаем приведенное уравнение электромагнитного состояния проводящей среды внутреннего проводника во временной области в виде

525   1 d5d5

, ++“ - = ° ci^o d r2 r о r

решение которого может быть получено методом разделения переменных, то есть путем представления искомого решения произведением двух функций К ( r ) • з ( t ) = 5 z ( r , t ).

Таким, что его подстановка в уравнение ⁽⁶⁾ и последующее деление на Ж г ) -3 ( t ) * ⁰ приводит к дифференциальному соотношению

1 d ² К 1 d К 1 d 3

+= ^Т^ ci Ц ₀,

К 2у^г   r К dr   3( t)     ^и дt

r

для которого равенство левой и правой частей может выполняться только тогда, когда эти части представляют собой некоторую постоянную разделения (- m 2 ), следовательно, это соотношение становится эквивалентным двум дифференциальным уравнениям вида

1 d 2 №    1 d R_ 1 d 3

+=       ^ri Цо      ,

R dr ²    r R dr   3 ( t ) c ¹^⁰ d t

d ³( t )^ 2^ A ⁽⁷ c 1^o—” + m ^ = 0.

5 t

Делением слагаемых уравнения (8) на постоянную m ² получаем вещественное уравнение Бесселя, в котором введена безразмерная переменная mr , а его частное решение определено двумя функциями Бесселя нулевого порядка (n = 0)

^{R (} r ) = AJ о ⁽ mr ) + BN о ⁽ mr ) ,

где A , B – постоянные интегрирования, но так как при r → 0 N ₀ → –∞, то постоянная B может приниматься нулевой.

Частным решением уравнения (9) является зависимость вида

3( t ) = C ■ exp

к ^c _c 1 ^ 0

t

Итак, для внутреннего проводника коаксиального кабеля в качестве частного решения уравнения (6) может приниматься произведение функций (10) и (11), которое должно удовлетворять начальным и граничным условиям с учетом особенностей процесса проникновения электромагнитного поля в этот проводник, изложенных в предыдущем разделе статьи, а именно тогда, когда процесс проникновения поля будет представлен в форме бесконечной суммы частных решений вида R ( r ) • 3 ( t ), дополняющей зависимость о $ ( z, t ) при соответствующих значениях ( nt_p + t ). Кроме этого, принимая во внимание условие нечетности мгновенных значений плотностей тока проводимости, устанавливаем, что здесь при малых t f ( t f → 0) должно выполняться равенство

^- Е AJ о ⁽ m i r ) exp —— ⁽р l = 1                    I ^ c 1 ^ 0

=⁵ 5 ( М+ Е A i J о ( m i r ) ^,

)                 i = 1

где A_l – коэффициенты разложения δ _z ( r , t ) в ряде Фурье-Бесселя, соответствующие последовательности постоянных разделения m l .

Постоянные m_l находят из условия обращения слагаемых ряда Фурье-Бесселя к их нулевым значениям при r = r 1 каждый раз, когда аргумент функции J 0 ( m l r ) становится равным ее корню к 0l с номером l , что позволяет записать (12) в виде

- i aj °

I = 1

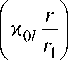
exp

( Л

-f М (°+) + iAJо

I T t )                i = 1

f A

r I K01 - I,

где T i - постоянная времени затухания l -слагаемого ряда ( 7 / = г о ci Ц о / К о i ).

Для нахождения коэффициентов A l в равенстве (13) используем свойство ортогональности бесселевых функций, по которому для функций J ₀ ( κ _{0 k} rr ₁) и J ₀ ( κ _{0 l} rr ₁) оно выражается в

том, что при любых положительных целых l ≠ k

r 1     (      r) f     r ^

I ^rJ o l ^K 0 k - I J o l ^K 0 1 - \^dr = ⁰, 0      I      r i J I      r i J

но при l = k

r 1                              2

f T 2 1       Г L _ Г 1 r2/ A

I ^rJ 0 I ^K 0 1^— I ^dr =     J 1 ( ^K 0 1 ) ,

0 v     r i V       ²

где J ₁ ( κ _{0 l} ) – функция Бесселя первого рода первого порядка от аргумента κ _{0 l} .

Умножением левой и правой частей равенства (13) на функцию rJ ₀ ( κ _{0 k} r r ₁) с последующим интегрированием от 0 до r 1 при l = k получаем соотношение

r ²

- Al '\ J 12 ( ^к 0 1 ) exP

(    ^            .2

-f | = 5<1)(0+)-LJi(коi) + Ai-L Ji(Koi),

V   T¹ )             ^K 0 ^{1                2}

из которого следует, что

^ l

■' 0+)

^к о IJ 1 ( ^к о I ) [ ! ⁺ exp ( - tpTi^" \

Таким образом, распределение плотности тока проводимости в сечении внутреннего проводника коаксиального кабеля определено зависимостью

2n     r i

i (t )=J d eJsW( r, t) rdr = 2n r б^ t)-4n^\ °+)x 00        2

“       exp ( - t^        7 ( r _

x^                         /tAI'J J° I K° l I rdr i=1 k°lJi(k°l>L1+exp(-tp/Tjj ° i    r1 J

exp (^- t^T

TO

= n r? ₅S\ t )-<)(. V-_TT-----—— , _                    l ^{= 1 K} ° l L ^{1 +} exp ⁽ tp/T JJ.

где5?.(t) = ^W2(t); 4»(0+) = ^Л7»)• n V2

Значение о ) ) (0 + ) определено здесь тем, что при t = 0 + сумма только двух первых блоков слагаемых усеченного ряда f 2 ( t ) равняется 0,9836, но добавление еще одного блока слагаемых увеличивает это значение до 0,9997.

Переходная проводимость g⁽¹⁾( t ) внутреннего проводника кабеля, как коэффициент пропорциональности между током i ( t ) и переходным напряжением u_S ( t ) на участке длиной Δ z , выражается формулой

(1)( t) = i (t) =      i (t)      = " ci (t) =

, ⁽⁾ _z ( i , )    А z 5 , ⁽ t )

n r^ ci _{1 4}3 < ¹⁾( 0 ₊ )f      exp ( - t/T i )

"^^ [ 1 - ⁴ S K 0 1 [ 1 + exp ( - t p/ T i ) ]

в которой множителем n r i а _c i /А z представлено значение конечной проводимости цилиндри-

- 1

<Х t ) = g ⁽¹⁾ ( 0 + )

R 1 ⁽¹⁾ ( 0 + )      g ⁽¹⁾ ( t )

• ¹    - 4 У ^ko i [ 1 + exp ( - tp!Ti ) \ _______^l =¹___________________________________

  
  

X                             _— 1

• ¹ - ⁴ У ^к"ш ^{[ 1 +} exp ( - ^tp /T l ) \ " - exp ( - tT ) = 1

0.2 0,4 0.6 0.8 1.0 1.2 1.4 1.6 1,8 2,0

Применительно к формуле (20) значения первых десяти корней κ _{0 l} функции J 0 ( x ) и соответствующих постоянных времени Tl , ограниченных двумя цифрами после запятой, представлены в табл. 1 для медного проводника при r 1 = 0,6 мм.

Относительные изменения переходного сопротивления внутреннего проводника ( r ₁ = 0,6 мм) коаксиального кабеля, подсчитанные по зависимости (20) при t_p = 0,1 мкс, показаны на рис. 3.

Особенности результатов численного анализа зависимости (20), изображенные на рис. 3, в том, что изменения переходного сопротивления заключены в диапазоне 10 % от начального его значения. Вместе с тем расчет по формуле (20) показывает, что переходная проводимость этого же участка проводника при t = 0 + равна только половине ее конечного значения ( Я ⁽¹ ) (0 ₊ ) ~ 0,489 п Гу С c ) при равномерном распределении плотности тока. Усредненное значение переходной проводимости g ₁ ⁽¹⁾ ( t ) ( t_p ) внутреннего проводника кабеля, определенное на интервале 0 <  t ≤ t p , при ограничении суммы бесконечного числа слагаемых в формуле (19) суммой их конечного числа N 1 , определено функционалом

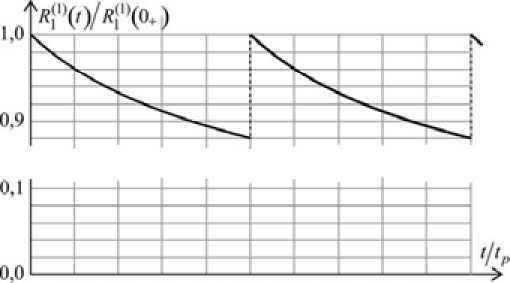
Рис. 3. Относительные изменения переходного сопротивления внутреннего проводника коаксиального

Таблица 1

Table 1

l 1 2 3 4 5 6 7 8 9 10 κ0l 2,41 5,52 8,65 11,79 14,93 18,07 21,21 24,35 27,49 30,63 Tl, мкс l 4,37 0,83 0,34 0,18 0,11 0,07 0,05 0,04 0,03 0,02 кабеля. Пояснения в тексте

Fig. 3. Relative change in transient resistance of the coaxial cable internal conductor. Explanation in the text

1 ^tp

{^ 1 ( t )) ( t p ) = — J £ 1 ( t ) dt = ⁿ r? ° c l t_{p 0}

4 M ^ f¹ - exp ( - t p/ Г , ) ]

1--/ ------;=---------------------------=r tp I=1 K01 [' + exp (-tp /T)]

который позволяет вычислить изменения усредненных значений сопротивления R(1(1)(t)} (tD) 1p внутреннего проводника кабеля при возможных переходах к более коротким длительностям биполярных импульсов. В частности, с уменьшением длительности импульсов вдвое отношение (^ t))(tp)/<^4 t»(tp! 2), вычисленное по формуле (21), показывает, что увеличение среднего значения ^(1)(t)^(tp/2) относительно прежнего составляет только 2,6 %. Это вполне согласуется с результатами вычислительного моделирования относительных изменений переходного сопротивления этого же проводника, представленными на рис. 3, а также с тем, что при исходном значении tp, равном 0,1 мкс, эти значения уже и так близки к их максимуму вследствие ограничения глубины проникновения электромагнитного поля ее пределом.

Получение этих численных результатов выполнялось с использованием данных табл. 1 так, что здесь была установлена приемлемость значения N ₁, ограниченного только первыми восемью слагаемыми, при котором различие составляло менее 0,5 % по сравнению с теми же расчетами при десяти слагаемых в формулах (20) и (21).

Анализ электродинамического состояния внешнего проводника коаксиального кабеля

Для внешнего проводника коаксиального кабеля затухание ( E_z , H _θ) – составляющих электромагнитного поля тоже характеризуется их уменьшением от максимальных значений на внутренней поверхности этого проводника, но математическая модель здесь уже не может приниматься аналогичной модели электродинамических состояний внутреннего проводника. Это обусловлено тем, что постоянные интегрирования B при функции N ₀( mr ) не могут приниматься нулевыми в частных решениях вида (10), в форме некоторой их суммы, удовлетворяющей начальным и граничным условиям. Внутренняя проводящая поверхность внешнего проводника здесь экранирует при нулевом ее потенциале, а источником первичного электромагнитного поля является внутренний проводник кабеля, что влечет необходимость учета коэффициента η отражения этого поля в процессе распространения этих импульсов по коаксиальному кабелю. На рис. 4 схематически показаны ( E_z , H _θ) – составляющие электромагнитного поля совместно с радиальной П r – составляющей плотности потока этого поля в произвольной точке M внутренней поверхности внешнего проводника кабеля.

Функция f 1 ⁽²⁾( z /υ) мгновенного профиля пространственного распределения поверхностной плотности тока проводимости отличается от функции f ₁⁽¹⁾( z /υ) только уменьшением ее уровня интенсивности в (1–η) r 1 / r 2 раз при том же пространственном полупериоде z n – z m = ( L 1 C 1 )^–1/2∙ t p . Граничные значения E_z ( r ₂, t ) при достаточно высоких частотах спектра и режиме согласования волнового сопротивления с нагрузочным почти обусловлены векторным полем плотности токов смещения так, что пространственно-временное распределение E_z ( r ₂, t ) можно определить суперпозицией гармоник поля. Комплексная амплитуда тока i k к -гармоники может приниматься зависящей от постоянной ( j ω _k μ₀σ _{c 2})^1/2 распространения электромагнитного поля в проводящей среде внешнего проводника кабеля и выражаться интегральным слагаемым вида

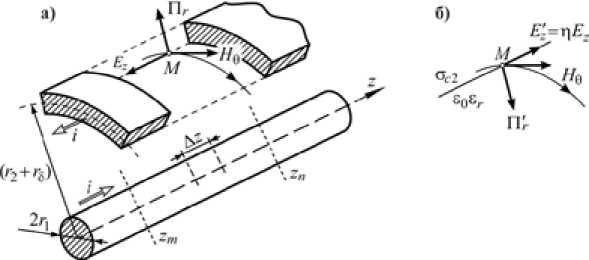
Рис. 4. Составляющие электромагнитного поля на внутренней поверхности внешнего проводника коаксиального кабеля схематически: a – в падающей волне на проводящую поверхность; б – в отраженной от проводящей поверхности. Пояснения в тексте

Fig. 4. The electromagnetic field components on the inner surface of the outer conductor of a coaxial cable are schematically: a – in an incident wave on a conducting surface; б – in a reflected from a conducting surface. Explanations in the text

2n A r

I k = J d ^e J a c 2 E z ( k )| r . exp [- ( a k + j P k ) , j ] ( , 2 + r _s) dr ,                (22)

00      ²

где Δ r – толщина внешнего проводника кабеля; α k , β k – коэффициент затухания и фазовая постоянная к -гармоники поля в проводящей среде ^{( a} k = ^ to к Ц о G 2 • cos л/ 4, p k = J to k Ц о O 2 • sin ^п/ 4).

При условии электромагнитной непрозрачности внешнего проводника кабеля, когда его толщина превышает глубину проникновения поля на основной гармонике, она может считаться бесконечно большой (Δ r → ∞) и вычислением по формуле (22) находим

2 -S , ( ^k )l r ₂

I k =

a k + jp k

-I TO

<

- r₂exp ( -a _kr _s- j p _kr ₈)

J 0

^^^^^^e

(         1

r8+---T^T I a k+j pk

-I TO

exp (-a krs-jp krs)

- 0

2nr2 5-(k) a k V2

n5 (k)|     v 2nr2 5Z(k)|

+ - rL e"j/2 « a k             a k 41

.

Форма результата (23) допускает и другую его запись в виде где   dk

I k = 2 K ^r 2 d k 5 _z ⁽ k ) eff ■ e

П/ , j /4

глубина проникновения поля k -гармоники  в проводящую

среду

( 1/2

d k = 1/a k = ( 2/( ro k Ц о ^ _c 2 ) ) ) ; 8 _z ( k ) ey - действующее (эффективное) значение плотности тока

= S z (. k )| r₂p- ) .

k -гармоники ( б z ⁽ k ) eff =5 z ⁽ k ) r2[41 ) .

Физическая интерпретация результата (24) в том, что значение тока İk здесь рассматри- вается как следствие равномерно распределенной плотности тока δz(k)eff по сечению цилиндрического слоя толщиной dk на поверхности радиуса r2 внешнего проводника кабеля малой длины. Итак, мгновенное значение тока во внешнем проводнике кабеля определено суммой k-гармоник:

N 2

i ( к ) = £ i_k ( t ) ;       к = 2 n - 1; n = 1,2,3, K ,

k где ik (t) = f2(t).

^{2 n r} 2 ⁵ _z ^{( k} )| a _k V 2

cos ( to k t -тс/ 4 ) , знаки которых определены знаками слагаемых функции

Переходную проводимость участка Δz внешнего проводника кабеля теперь находим аналогично формуле (19) в виде зависимости

N ₂ N ₂

g ^{(2) (} t ’ = т& = ^к 2 ^ i k ⁽ t ) ^^k , t ) u s ⁽ t )                   k Ik

по которой при N2 = 12 и единичной длине (Az = 1) кабеля определяются значения g[ \0+) и {g(2)(t»(tp) на интервале — tpl2 < t< tp/2 формулами дП 0+И ^ c 2

d 1

d- - di - d 7 _{+ +} d 23

3   5   7 ^K 23

(g (²⁾ ( t »( t p ) =

1 ^tP / \( t ) dt/^{< P} / ² U s ( t ) dt .^{t p -} t p /2        / - t p /2

= V2n r₂ a_cl ^c

d 1

d ₃

d 5 d 7 d 9

5 ²   7 ² 9 ²

—

₊ d 23 -1 145» + 23 2 j 1,145

” 1,62 "nr2Cc2

d 1

d ₃

^d 5   ^d 7   ^d 9        ^d 23

--—I— ------- —I— ------ --- —I— ---------

5 ²   7 ²   9 ²       23 ²

.

При получении этих формул на основе зависимости (26) входящие в ее числитель и знаменатель множитель 16 ©о/(n2 V2) и функцияf1(2)(z/и) опущены. Суммирование величин, обратных к усредненным значениям переходных проводимостей внутреннего и внешнего проводников кабеля, определенных приближенными аналитическими формулами (21) и (28), позволяет определить не только усредненное значение R1(t) (tp) сопротивления коаксиального кабеля на единицу его длины, но и коэффициенты пространственного затухания ac = 0,5 Ri 1(t )^(tp),JcjLi

и временного затухания вc = (R 1(t))(tp)/(2L1), в которых значения L1 и C1 полагаются не зависящими от параметров импульсных сигналов, а поперечная проводимость G1 кабеля на единицу его длины достаточно малой.

Если результирующее экспоненциальное затухание, вносимое поверхностями внутреннего и внешнего проводников коаксиального кабеля, принимается здесь пропорциональным его длине, то коэффициент временного затухания может рассматриваться только как показатель , степени вносимых средой передачи искажений формы принимаемых сигналов в сравнении с известными их значениями для другой коаксиальной среды передачи той же длины.

Заключение

На основе анализа модели распространения импульсных сигналов по коаксиальному моноканалу ЛВС получены приближенные аналитические зависимости переходных проводимостей и их усредненных значений для проводящих поверхностей внутреннего и внешнего проводников кабеля. Исследуемая модель содержит учет ненулевых длительностей фронтов передаваемых импульсных сигналов на входе коаксиального кабеля, которые в целях конкретизации результатов анализа определены четвертью длительности тактовых интервалов, а также две раздельные математические модели процесса проникновения электромагнитного поля импульсов в проводящие поверхности кабеля, разделенные средой с малыми диэлектрическими потерями. Результаты анализа представлены разложениями по гармоникам поля передаваемых импульсных сигналов манчестерского кодирования при использовании коаксиальных кабелей различного типа.