Электродинамический анализ собственных волн многопроводной полосковой линии передачи

Краевые задачи для ряда направляющих структур СВЧ и КВЧ диапазонов могут быть сформулированы в виде векторных интегральных уравнений первого рода. Элементы ядер таких уравнений представляют собой бесконечные ряды и содержат в неявном виде логарифмические особенности и сингулярности Коши. Применение к такому уравнению проекционной схемы требует усечения рядов в ядре. Последнее означает замену сингулярного ядра ограниченной функцией. Но, как известно, решение интегрального уравнения первого рода с ограниченным ядром представляет собой некорректно поставленную задачу [1]. В результате, приближённое решение приобретает неустойчивость и проявляет относительную сходимость [2].

Эффективный путь преодоления указанных трудностей заключается в переходе к уравнению второго рода на основе процедуры частичного обращения исходного интегрального оператора. С помощью данной методики было решено большое количество краевых задач прикладной электродинамики, допускающих формулировку в виде интегральных уравнений, определённых на единичных интервалах [3]. В [4] метод частичного обращения оператора был обобщён на случай направляющей структуры с несколькими щелями.

Настоящая работа посвящена исследованию экранированной многопроводной полосковой линии передачи (ЭМПЛ), поперечное сечение которой изображено на рис.1. На границу диэлектрических слоёв 1 и 2 нанесено произвольное количество бесконечно тонких идеально проводящих полосок. Направляющая структура помещена в прямоугольный экран. Потери в экране и средах заполнения считаются пренебрежимо малыми.

Интегральное уравнение первого рода

Задача о собственных волнах ЭМПЛ может быть сформулирована в виде векторного интегрального уравнения первого рода [3]

J Kt ( x , x J ( x ' ) dx ' = 0, ( x e X )     (1)

X

Здесь X - совокупность интервалов оси x , соответствующих металлизированным участкам границы областей 1 и 2 (рис.1)

L

X = U X j , X j = ⁽ x j 1 , x j 2 )

j = 1

r

Вектор j содержит искомые компоненты плотности поверхностного тока на полос- ках j , j zx

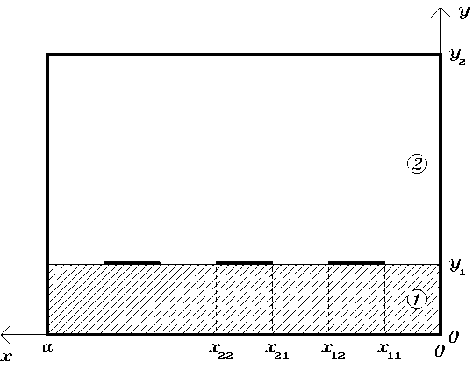
Рис.1. Поперечное сечение ЭМПЛ

J = ( Jz (X ),-a J X (x ) l П

K 2 j

~

r 2 j a

Ю

^ COS P mx Sin P mx'

m = 1

Штрих при J x означает производную по аргументу. Элементы ядра представляют собой тригонометрические ряды:

2 “

K11 =-У Zm11sinPmxsinpmx', a m=1

^

K12 =- y — Zm12Sin Pmx sin Pmx, am m=1

^

K21 =- XZm21COSPmxSinPmx’ a m =1

K 22 = Z 022 ^ 1 ^{— +}

a

2 “ 1

+ -У —Zm22 COSPmxsinPmx', am m=1

1           Sin P, x '

r2 j                        ,

a J cos P1 x - cos P1 x'(j = 1,2)

Очевидно, что на множестве

L

X ² \ U X 2 элементы ядра ограничены. По- j = 1

этому сингулярные части функций K ij можно представить в виде:

K 1 Si = I ( x , x ')— r j ln

1 j             _a

^K 2 ^S ) = I ⁽ x , x ') ¹ Г 2 j j_a

sin ( P 1 ( x ' + x ) l 2 )

sin ( P ₁ ( x '- x ) /2 ) ’ sin P1 x'          (3)

COS P 1 x - COS P 1 x ’’

где P _m = n m I a , Z mij - элементы тензора импедансов, выражаемые через частоту колебаний, а также поперечные размеры и проницаемости диэлектрических слоёв 1,2 (рис.1).

Последовательности Z_mi j удовлетворяют следующим предельным соотношениям:

^{lim ( mZ}m11 ) = r _n, ^lim Z m 12 = ^r 12 , m ^^            m ^^

^lim Z m 21 = ^r 21 ’ ^lim ( m ^-1 Z m 22 ) = ^r 22 - m ^^           m ^^

где I ( x , x ' ) - индикатор множества

1,

0,

L

U Xj j=1

(.       L.

^{( x} , ^{x )} E [^ X j

A

/

L

A

( .x , x ') _E X ² \ U X j ²

I                ^j = 1      J

Введём функции:

Явный вид величин Z mij , r ij приведён в [3]. Подставляя в (2) вместо импедансов их асимптотики, приходим к выводу, что функ

K 1 ⁽ S ) =- 1 ( x , x ') — r 1 j ln|2 ( cos P 1 x '- cos P 1 x ) ,

T~ 2 Sj ) = I ( x , x ') 1 Г 2 j

sin P 1 x

cos P1 x - cos P1 x ’’

ции Kij имеют особенности при x = x'. А именно

На основании соотношений:

K 1 j

~ r j a

“ 1

7 — Sin Bm x Sin Bm x' = mm

m m =1

K S - K j = I ( x , x ')- r 1 j ln2sin P 1

x ' + x

1    . Sin (B₁( x ' + x ) I2 )

- r i ln .    1, a J   sin(P1 (x'-x)I 2)

к ^{( S} )

K 2 j

^{- K} 2 S ) = I ^{( x} ’ ^x ') ^{1 r} 2 j ^C tg ^P 1 ^x4^x ’ ^j a           2

можно сделать вывод, что элементы тензоров Kt ⁽ S ) и K ( S ) имеют идентичные особенности.

Запишем интегральное уравнение (1) в виде

„ , ( . 0(v')+0(v)1"

+ 2 r , ln I sin——--— +

¹ j l 2 I

^

^{+ ( 1 -} T ^{( v} , ^v l^A m 1 j u m - 1 m = 1

1 ^{( v} ) u m - 1 ^{( v} ' ) .

7

J [ ( k ( x , x ' ) - K ⁽ S ) ( x , x ' ) ) +

X

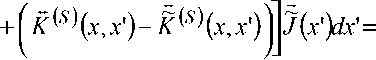
= - j K ⁽ S ) ( x , x' ) J ( x' ) dx ',      ( x e X )

X

'

P 2, R )=-- Z 02₂ e ( v^ п

2 j + ~ ⁽ v , v ') X

V

^X 2 ^ m A m 2 j t m ^{( v} ) u m - 1 ^{( v} ' ^{) +}

Выполняя замену переменных v = cos P1 x, v' = cos P1 x', имеем j P(R)(v, v ')r (v ')dv' = -j P(S )(v, v ')rj (v ')dv', VV

( v e V )                                (4)

Областью определения последнего уравнения служит совокупность интервалов

L

V = U V j , V j = ^{( v}j 1 , ^vj 2 )

j = 1

v j i = cos P i x L + 1 — j ,2 , v j 2 = ^cos P i x L + 1 — j ,1 .

Искомый вектор j имеет вид

_ m = 1

+        ctg ^(v^^+^fv^

. -T72       2

^

+ (1 -1 (v, v'))2^^ mA m=1

f

+

1

m 2 j t m ^{( v} ) u m - 1 ^{( v} )

7

где 3 ₂ j - символ Кронекера,

T ( v , v ' ) =^

1,

0,

r (v )=-4

т f a        11

^J z I -arccos ^v

l П              J

-

V

a _, f a

—J _x I — arccos v

П l П

7

Сингулярная p ^{( S} ) и регулярная P t ⁽ R ) ча

сти ядра задаются соотношениями:

~/W х 1       / ln| v '- v|

P ^{( S} ) ( v , v ') = -1 ( v , v 1 ^{1     1}

п I 0

0 1

( v ' - v ) ^-1/

P       п f 7(v • v' r,j

V L

ln2 +

^

+ 2 ^^^m1 jum-1 (v)um-1 (v ) + m=1

f, . , ^L, , ⁽ v , ^{v )e} U V j

V          j = 1

1

7

L

1

V

( v , v ' ) e V ² \ U V,² j = 1     7

- индикатор множества

L

U Vt j=1

t

~ A _m

1^f mZ m ^{11    Z}m 1 ²

m V Z m 21   m - Z m 22 J

t     ^r11

r =

V ^r21

r ¹² , r ₂₂ 7

t

A _m = A _m - m ^-1 t , 0 ( v ) = arccos v ,

функции t_m , u_m выражаются через много

члены Чебышёва первого T_m и второго U_m рода:

t m ^{( v} ) = г^—T ^T m ^{( v}) u m ^{( v} ) = V 1 - v 2 U m ^{( v} ).

V1 - v ²

Обращение интегралов

Рассмотрим интеграл

¹ J7( v , v ')^ dv' = f ( v ), ( v e V ),    (5)

n ^J         v ' - v

V ядро которого содержит сингулярность Коши (v'_v)-1. Будем предполагать, что функция ф(v) удовлетворяет условию Гёльдера [5] внутри интервалов Vj и допускает интегрируемую бесконечность на их концах. Введём системы функций тu^F- 'a + biv) (ve VA , n () [0,             (v e V \ Vj )

U ( j )_WJ U « ⁽ a j ⁺ b j v 1, ^{( v e} V j 1, .

n ⁽⁾ [ 0,               ( v e V \ V j )

определяемые через многочлены Чебышёва. Здесь величины a j и bj подобраны так, чтобы линейное преобразование uj = aj + bjv переводило Vj в интервал (-1 < Uj < 1):

vj 2 ⁺ vj 1     к ^

a j =--, bj =-----------, vj 2 - vj 1          vj 2 - vj 1

G' = VL)

Очевидно, что системы T n^j ) ( v ) и U n^j ) ( v ) ортогональны на множестве V с весовыми функциями Q ^-1 ( _v ) и Q ( v ), соответственно, где

Q ^{( v} ) = 1 ¹ - a + j ) 2 , ^{( v} e V j ) ( j' = 1, L Ji Ядро интеграла (5) допускает следующее представление

L ^

U , v ' )     = 2У b jY v М ) ( _У ) t ( j ) (V) (6)

v'-v j=1    n=1

Умножая обе части (5) на U n- 1 ( v ) Q ( v ), ( j' = 1, L ; n = 1,2, K ) и интегрируя по V , находим

T n ) = J f ^{( v} Un- 1 ^{( v} ) Q ⁽ v ) d ^v ,   (7)

2b jV где

^ nj ) = a j 1 1*^{ф( v ) t (} j ^{) ( v} ) d ^{v n ( 1 + §} 0 j )l

V

- коэффициент Фурье в разложении

L “

9 ( v ) = Q -' ( v ^I jUv >    (8)

j = 1 n = 0

Подставляя (7) в (8) и вновь учитывая соотношение (6), получаем следующую формулу обращения для интеграла f ( v )

L

T ^{( v} )=т;п£ф 0 j ^{) t} 0 ⁽ j ^{) ( v )-}

^{Q ( v} ) j = 1                               (9)

—Т1П J~ ⁽ v , v ') Qv ) f ⁽ v')dv ', ⁽ v ^{e V} )

ⁿ Q ⁽ v ) V        v' - v

Рассмотрим интеграл с логарифмической особенностью

• ¹    f/ ( v , v *) ln| v '- v |ф ( v')dv' = g ( v ), ( v e V ) (10) П

V

Продифференцировав (10), получаем сингулярный интеграл вида

• ¹    J~ ( v , v ’^v ) dv' = - g' ( v ).

n ^J         v' - v

V

На основании формулы обращения (9), имеем

^(v )=Q(v) ]E ^-j )T0° )(v)+ v j=1        '                (11)

⁺         f~⁽ v , v ') Q ⁽ v j g ' ⁽ v ^{,) d} v '.

n Q ( v ) J        v ' - v

Определим коэффициенты ф0j)• Умно- жим (10) на Tjj)(v Q 1 (v), (j' = 1, L) и проинтегрируем. С учётом соотношения

1 ~                     dv      ln(2bj)

I ⁽ v , v > v '- VT _D ⁽ j ⁾⁽ v )     =--'

n                      Q (v)      bj находим

-^^ ’* J g ( v T j ) v ) Ш • (12)

Подставляя (12) в (11), получаем формулу обращения для интеграла g ( v )

ры выбирались следующим образом: у/а = 0,1; у 2 /а = 0,5; x 11 /a = 0,35; x 12 /a = 0,45; x 21 /a = 0,5; x₂₂/a = 0,65; проницаемости диэлектрических слоёв: £ ⁽¹⁾ = 10, £ ⁽²⁾ = ц ⁽¹⁾ = ц ⁽²⁾= 1.

На рис.2 представлены зависимости фазовых (кривые Р1, Р2) и групповых (кривые G1, G2) скоростей основной и первой высшей волн ЭДПЛ от волнового числа свободного пространства k = ш c. Как следует из графиков, с увеличением частоты колебаний нормированные фазовые и групповые скорости обеих волн асимптотически приближаются к предельному значению

T ⁽ v ) =

п Q(v )

J ~( v , V) ^

v ' - v

V

g ' ( v >'

-

v =    1

С" l / ¹^^^

= 0,3162

-Ji j j № (V) ^

V j = 1 ^j

, (13)

(v e V )

В результате применения формул обра-

( 5 ) щения (9),(13) к интегралам с ядрами Pj , равенство (4) преобразуется в интегральное уравнение второго рода. Для решения последнего может быть использован проекционный метод. При этом элементы вектора Г разлагаются в ряд по системе функций T ! ^j ’ ( v Q - ( v ) :

соответствующему скорости распространения идеальной поперечной волны в среде с про-ницаемостями £ ⁽¹⁾, ц ⁽¹⁾. Таким образом, предельные переходы у _ф ^ V , У Г_Р ^ v можно рассматривать как следствие увеличение увеличения относительной части энергии волны ЭДПЛ, сконцентрированной в области 1, имеющий более высокую оптическую плотность.

Следует отметить, что на некоторой частоте групповые скорости волн равны между собой. Предположим, в двухпроводной полосковой линии передачи возбуждается амплитудно-модулированный сигнал. При этом высокочастотное заполнение распрос-

L ^

j.(v ) = Q - ( v ) ££ &T k^k ) ( v ) ( i = 1,2 ) (14) k = 1 n = i - 1

Равенство нулю коэффициентов j 2 k ) ( k = 1, L ) является следствием поведения поперечной составляющей плотности тока на рёбрах проводящих полосок

^J x ^{( X} k1 ) = ^J x ^{( X} k2 ) = ⁰ , ^{( k} = 1» L ) ■

Результаты расчётов

В дальнейшем положим L = 2 рассматривая экранированную двухпроводную полосковую линию передачи (ЭДПЛ). Числовые значения параметров направляющей структу-

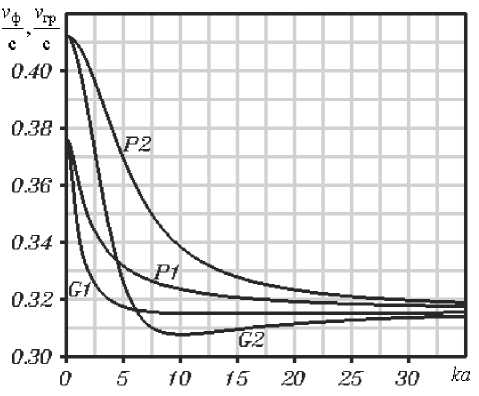
Рис.2. Зависимости фазовых и групповых скоростей волн ЭДПЛ от волнового числа (P1 - v ф,1 ; P2 - v ф,2 ; G1 - v гр,1 ; G2 - v гр,2 )

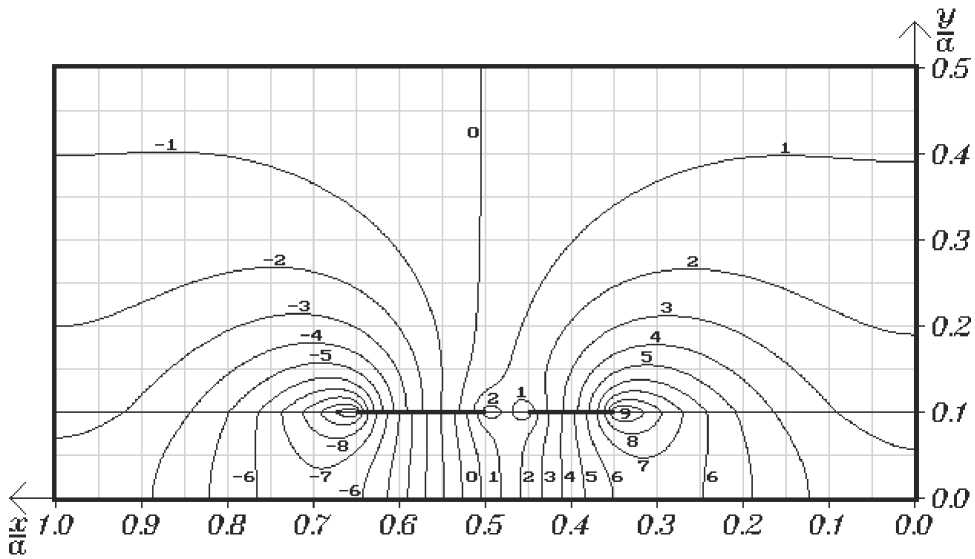
Рис.3. Распределение функции H z ( x , y ) / у ^ для основной волны ЭДПЛ

траняется с фазовой скоростью рабочей волны. Если сигнал узкополосный, то можно приближённо считать, что огибающая переносится с групповой скоростью волны [6]. На любой частоте волны 1 и 2 будут одновременно возбуждаться в ЭДПЛ. Вследствие различия их групповых скоростей, на выходе линии передачи огибающие сигналов, переносимых обеими волнами, окажутся сдвинутыми по фазе. Обусловленное этим искажение модулирующего сигнала можно исключить, выбрав частоту несущего заполнения вблизи абсциссы точки пересечения кривых G1 и G2.

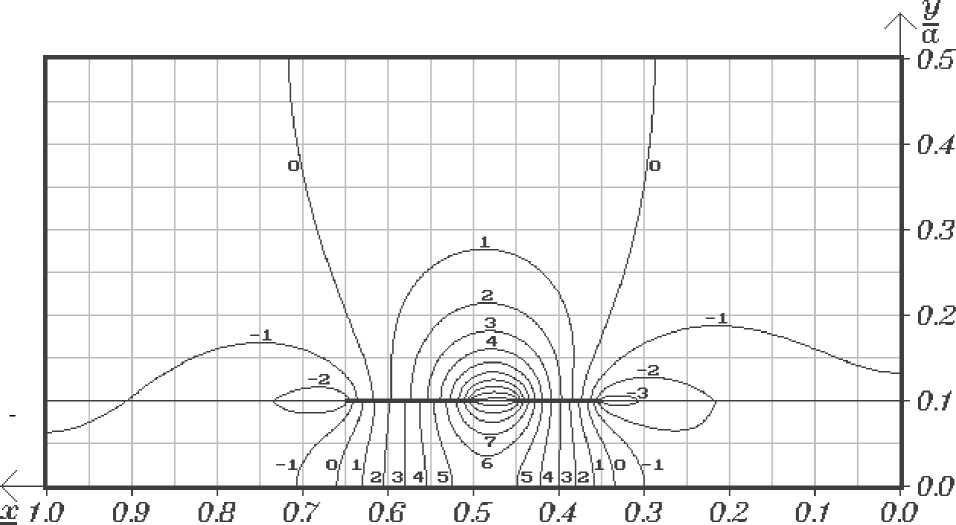
Рис.4. Распределение функции H z ( x , y ) / у Ю для первой высшей волны ЭДПЛ

а

При построении графиков производилось усечение рядов (14) на слагаемых с индексами n = N, где N = 2. В каждом из элементов ядра интегрального уравнения второго рода учтено по M = 28 слагаемых. При этом абсолютные погрешности определения нормированных фазовых и групповых скоростей волн не превышали значения A v / c = 0,0004.

На рис.3 и рис.4 представлены распределения комплексных амплитуд продольных составляющих напряжённости магнитного поля волн 1 и 2 в поперечном сечении ЭДПЛ. В качестве нормировочного множителя использован один из коэффициентов Фурье в разложениях (14). Предельные индексы суммирования выбирались равными N = 2, M = 500. Как видно, линии уровня, соответствующие максимальным значениям H_z , локализованы вблизи границы областей 1 и 2 (рис.1).

Заключение

Модификация метода частичного обращения оператора, предложенная в настоящей работе, может быть использована при решении задач дифракции волн на металлических решётках в однородно заполненном прямоугольном волноводе, а также при анализе па- дения плоской электромагнитной волны на частично металлизированный диэлектрический стержень.

Работа выполнена при поддержке гранта ТОО ‒ 2.4 ‒ 2171 Министерства образования Российской Федерации.