ЭЛЕКТРОФОРЕЗ НА СУММАРНОМ ПОСТОЯННОМ И ПЕРЕМЕННОМ ЭЛЕКТРИЧЕСКИХ ПОЛЯХ. I. ПЕРЕМЕННОЕ ЭЛЕКТРИЧЕСКОЕ ПОЛЕ, КРИТИЧЕСКИЙ ОБЗОР СОСТОЯНИЯ ВОПРОСА

Изучению возможности увеличения подвижности ионов и дисперсных частиц при капиллярном электрофорезе в настоящее время уделяется повышенное внимание. Этому способствуют выявленные в последнее время эффекты, связанные с нелинейной зависимостью между подвижностью ионов (дисперсных частиц) и приложенным электрическим полем (см., например, обзоры [1–3], а также [4, гл. 10]). Причем в разных случаях возникает различная прямая степеннáя зависимость между скоростью частицы и напряженностью приложенного электрического поля. Обычно эти зависимости рассматриваются для случая постоянного электрического поля.

Кроме прямого влияния на подвижность частиц вследствие нелинейной зависимости между скоростью частиц и напряженностью приложенного постоянного электрического поля, следует отметить также сравнительно недавно открытый и исследованный эффект возникновения в окрестностях частиц при приложении переменного электрического поля целого спектра разнообразных течений различной интенсивности [5, 6] (см. также библиографию в них). Все эти течения имеют общую особенность: их скорость квадратично зависит от напряженности приложенного электрического поля [5, 6]. В работе [6] рассматриваются нелинейные течения, вызванные поляризацией двойного электрического слоя (ДЭС), в то время как в работе [5], кроме этого, рассмотрено еще два механизма, обуславливающих возникновение стационарных нелинейных течений: инерционного и элек-трокапиллярного.

В работе [5, с. 65] приведены данные о том, что скорости электрофореза в открытом объеме при постоянном электрическом поле более чем в 25 раз превосходят скорости стационарных течений при приложении переменного электрического поля при одинаковых величинах амплитуд напряженностей электрического поля. Однако в условиях капиллярного электрофореза заряженных частиц вполне может оказаться целесообразным совместное использование и постоянного, и переменного электрических полей. Для этого необходимо критически рассмотреть выбор математического формализма и физических моделей рассматриваемой проблемы.

ПОСТАНОВКА ПРОБЛЕМЫ

Настоящая работа посвящена случаю, когда электрофорез осуществляется на переменном электрическом поле. Целью настоящей работы является критический обзор известных в настоящее время посвященных этому вопросу работ, оценка выбора физических и математических моделей, посвященных электрофорезу на перемен- ном электрическом поле. Существует несколько механизмов образования стационарных течений жидкости в окрестностях частиц. Здесь будет рассмотрено два из них: инерционный и поляризационный механизмы образования стационарных течений в условиях приложения переменного поля. Рассмотрение сопровождается массированными ссылками на работы [5, 6], в которых приведена обширная библиография по анализируемому вопросу.

ИНЕРЦИОННЫЙ МЕХАНИЗМ ОБРАЗОВАНИЯ СТАЦИОНАРНЫХ ТЕЧЕНИЙ

ПРИ ВОЗДЕЙСТВИИ ПЕРЕМЕННОГО ЭЛЕКТРИЧЕСКОГО ПОЛЯ

Воздействие на дисперсные частицы переменного электрического поля вызывает их колебательные движения. В этом случае причиной возникновения стационарных течений в окрестности частиц служат инерционные эффекты. Для этих течений, как упоминалось выше, характерна квадратичная зависимость скорости от амплитуды напряженности электрического поля. Данный эффект проявляется как для твердых частиц, так и для капель, совершающих колебательное движение относительно их сферической формы [5, с. 112].

В работе [5, гл. 4] для исследования заявленной тематики за основу берется неусеченная система гидродинамических уравнений Навье—Стокса для несжимаемой вязкой жидкости (см., напримр, [7, § 16]; [8, с. 39, 44]):

f дv        ,_,),_,р\ — + v - Vv I = -Vp + nAv,

V - v = 0 . (2)

Здесь v — вектор скорости течения жидкости; ρ и p — соответственно ее плотность и давление в ней; η — динамическая вязкость жидкости.

Отметим, что при рассмотрении этого механизма не принимается допущение о малости числа Рейнольдса , равного отношению инерционного члена v - V v к вязкому члену n A v , и тем самым не отбрасывается нелинейный инерционный член в уравнении (1), что привело бы к линеаризации уравнения движения (1) и соответственно к невозможности моделирования нелинейного течения, которое не может возникнуть в задаче, описываемой линейной моделью. Задача решается в терминах безразмерной функции тока для осесимметричных течений в свободном пространстве. Рассматривается сферическая частица. Тогда (размерные) компоненты вектора скорости v ( V R , V ₀ , t )

можно представить через безразмерную функцию тока для сферических координат [5, с. 113] (см. также Приложение 1)

= - U о дФ V = U о дФ r ² sin О дО ’    ⁰ r sin О дr "

Здесь r = R / a — безразмерное расстояние от центра частицы, где a — радиус сферической частицы; U0 — амплитуда скорости колебательного процесса; Ф — безразмерная функция тока, ψ равная Ф =     , где у — размерная функция

U ₀ a ²

тока, описанная в Приложении 1; ( R , 0 , ф ) — исходные сферические координаты, отсчитываемые из центра частицы.

После применения к (1) оператора ротор V х получается следующее общее выражение для вычисления функции тока Ф в сферических координатах [5, с. 113]:

E 4Ф- Re - sin О

дФ д дФ д — дО дr дr дО

- 2 ^f a ) — E ²Ф = 0.

I 5 ) д т

E 2Ф r2 sin2θ

aU

Здесь Re = —- — число Рейнольдса процесса;

v = n / Р — кинематическая вязкость; 5 =

1/2

I 2v I              к

= I — I — глубина проникновения вязкой вол- k ^ю )

ны; E ² — оператор Стокса, равный в сферических

_            д2  sin0 дГ 1 д| координатах [8, с. 125] E2 =—-+-------,

дR2   R2 дО ksin0 дО)

а применительно к (4)

,2 д2    sin 0 д Г 1 д '

2 = —г + —г"—I       I

дr2    r2 дО k sin 0 дО )

[5, с. 113];

т = to t — безразмерное время; ю — угловая частота переменного электрического поля.

Нелинейное по Ф уравнение (4) решается итерациями с помощью разложения

Ф = Ф ₀ + Re Ф 1 + ( Re ) 2 Ф ₂ + ... .     (5)

Вначале получено из (4) решение Ф ₀ ( r,0,t ) = F₀ ( r , 0 ) e ^{- 1 to t} при Re = 0. Решения Ф _n , n = 2, 3, 4,... могут быть получены итеративно после подстановки разложения (5) в (4) и последовательного нахождения решений Ф ₁, Ф ₂,^ .

Следующее решение ищется в виде Ф 1 ( r,6,t ) = Ф a ( r , 6 ) + Ф _t ( r , 6,t ) , а стационарное течение подчиняется уравнению

E4ф a = sin 6 x x /Г d Re (Фо) £ d Re (Фо) d \|_   d6    dr      dr    S6

^E ’^R e ( ^ф 0 ) \

^, (6) r ² sin² θ

где        означает усреднение по времени, a Re (Ф0) — действительная часть Фо.

В [5, § 4.2] найдено решение (6) для стационарных течений в окрестности осциллирующих жидких капель, в [5, § 4.3] такое решение найдено для осциллирующих жестких сферических частиц.

В заключение данного пункта отметим, что при нахождении стационарных решений, вызванных инерционными свойствами как жидкости, так и включений, нелинейность учитывалась только в уравнении движения Навье—Стокса (1). Краевые условия, принимавшиеся в задаче, оставались линейными.

ПОЛЯРИЗАЦИОННЫЙ МЕХАНИЗМ

ОБРАЗОВАНИЯ СТАЦИОНАРНЫХ ТЕЧЕНИЙ ПРИ ВОЗДЕЙСТВИИ ПЕРЕМЕННОГО ЭЛЕКТРИЧЕСКОГО ПОЛЯ

План изложения

Поляризационный механизм достаточно хорошо изучен (см., например, [4, гл. 6–8]; [5, 6]; [9, гл. 9]; [10, гл. 3, 4, 11]; [12]).

Далее рассмотрим последовательно поляризацию незаряженных или слабо заряженных частиц, когда отсутствует необходимость учета механизмов концентрационной поляризации и поверхностной проводимости частиц [5, 6]. После чего коснемся более сложного механизма поляризации частиц, когда этими механизмами пренебречь нельзя [11, 12]. Остановимся и на случае сильно заряженных частиц, когда проявляется качественно новый эффект, связанный с наличием у них объемного заряда, квадратичного по напряженности электрического поля [13].

Поляризация слабо заряженных частиц

Общая постановка задачи [5, гл. 5]; [6]

Система уравнений, описывающая рассматриваемый процесс, состоит из гидродинамического блока, включающего модернизированное для малых чисел Рейнольдса уравнение движения (1) (называемое в этом случае уравнением Стокса) и уравнения непрерывности для жидкости (2) (будем далее рассматривать случай совместного дей- ствия постоянного E0 и гармонического E1 векторов электрической напряженности), а также уравнения непрерывности потока катионов и анионов (см. Приложение 2) и уравнения Пуассона для потенциала электростатического поля (см. [10, §§ 3.1 и 3.2], а также [5, с. 157]; [6])

d V

P — = -Vp + n^V + PeE0 + PeE1, )

d t

V-v = 0,(8)

V-j +-c7 = 0,(9)

at

Аф = -4^Pel-     (в СГСЭ).(10)

ε

Здесь рассматривается случай симметричного электролита с модулем зарядного числа ионов Z и концентрацией зарядов положительного c ⁺ и отрицательного c ^- ; р _e — плотность электрического заряда; ε , ε ' — соответственно диэлектрическая проницаемость жидкости и частицы. В качестве вектора j ± рассматривается плотность потока этих ионов (см. Приложение 2, (П6))

±     ±          ГЛ±Х"7 ±     ± j = С Vmigr - D V- C + C V =

= ± c ± p ± E - D ± V - c ± + c ± v ,          (11)

где µ — подвижность ионов; D — коэффициент диффузии; E — вектор напряженности приложенного электрического поля.

Далее будем рассматривать стационарную и нестационарную задачи отдельно.

Нестационарная задача . Диэлектрическая частица в проводящей жидкости [5, § 5.1.1]; [6]

Принимается, что в декартовых координатах поле E j ориентировано вдоль оси Oz : E 1 ( 0,0, E 1 ) , где E 1 = E j e~^{1 m t} . Электрическое поле E , изменяет концентрации положительных c ⁺ e~'^mt и отрицательных c ^- e~'^at ионов. Результирующая плотность заряда ρ _el в (10) определяется из выражения

P ei ( R ,6, t ) = Ze ( c ⁺ ( R ,6 ) - c ^- ( R ,6 ) ) e - ^{m t} =

= Ze5c ( R ,6 ) e ”'^mt .                  (11)

¹⁾ Отметим, что в оригинальных работах [5, 6] автор рассматривает однородное уравнение движения (7). В качестве источника фигурирует только переменное поле E ₁ . Действие этого источника проявляется в [5, 6] в краевом условии и в распределении поля в отсутствие поляризации.

Здесь e — заряд протона; 3c = c ⁺ - c — разностная концентрация ионов.

Пусть 3c ± ( R , 9 ) e ^{- i} “ t = c ± ( R ,9 ) e - i “ t - c 0 — невязки концентраций катионов и анионов относительно их равновесной концентрации c ₀ .

Допущение 1

Принимается допущение о малости числа Пекле Pe = Va / D ^ 1, где V — характерная величина амплитуды скорости; a — радиус частицы; D — коэффициент диффузии ионов (принимается одинаковым D = D ⁺ = D - ). Как показано в [10], это условие справедливо даже для заряженных частиц в случае слабой поляризации, т.е. при условии

3c ± ( R , 9 ) <  c о .               (12)

При Pe ^ 1 в (11) можно пренебречь конвективным членом c ± v . После этого система (7)-(10) распадается на две независимые подсистемы: гидродинамическую (7), (8) и электрическую (9), (10). Задача поляризации таким образом решается с помощью только электрической системы (9), (10).

Для упрощения выкладок принимается также допущение о равенстве коэффициентов диффузии D = D ⁺ = D - и подвижности ц = ц ⁺ = ц - ионов. Тогда (9) сводится к одному выражению

- i ®3 c = D A 3 c + 2 c ₀ ц А ф .        (13)

Окончательно из (10) и (13) получено

A 3 c = y 2 3 c ,                (14)

где у 2 = к ² - i ® / D ; к = Л "¹; Л — длина Дебая. Подставка решения (14) в выражение для p el = Ze 3 c ( R , 9 ) , а затем в уравнение Пуассона (10) и учет граничных условий на границах дает окончательно для диэлектрических частиц

ф ( R , 9 , t ) =

= фо (R,9,t) + фd (R,9,t) + фр (R,9,t),(15)

3c(R,9,t) =       фр (R,9,t),(16)

4πZe где

Ф0 (R ,9, t ) = - E1R cos 9e "“,(17)

Ф d ( ^{R ,9,}t ) = a³E , cos ^{9 x}

R

. 2 ^{1 +} I v 1^{(1 - Y}a ^{) 2 +} 1 ]^{-( Y}a ^{) 2}

3K ^ ок у¹-

2 ^Y ^ 1 + ^ 7 ^[ ( 1 + Ya ) 2 +1^|- ( ка ) 2

ф р ( ^{R, 9 ,}t ) =

3 aE 1 e"^{Y (} R ^- a ) γ R

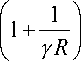
( к a ) 2

1 + ^{2 7} )[ ( 1 + Y a ) 2 + 1 J- ( к а ) 2

Здесь ϕ ₀ — потенциал, вызванный исходным полем E ₁ , определяемый из условия, что напряженность, соответствующая потенциалу, равна

E ( R, 9 ,t ) = E ( R , 9 ) e - i ^{m t} ,

E ( R , 9 ) e - “ t l    = E ,

R ^m где E1 определен выше:    E1 (x, y, z, t ) =

= ( 0,0, E 1 ) e”^imt , E = const.

Составляющая ϕ _d (19) суммарного потенциала, вызванная поляризацией частицы, представляет собой осциллирующий дипольный момент. Наконец еще одно следствие поляризации, вызванной внешним электрическим полем, — появление скачка потенциала ϕ _p .

Как видно из (15)–(19), пока все решения исходной системы (9), (10) линейны, являются гармоническими функциями частоты ω исходного электрического поля (отсутствуют постоянная составляющая и кратные гармоники).

Допущение 2. Тонкий двойной слой

Выполняются условия тонкого двойного слоя к a ^ 1, частота поля много меньше частоты максвелл-вагнеровской поляризации го «^ Dк ². В этом случае выражения (16), (18) и (19) упрощаются [5, 6]:

(п п Л a ^{E 1 cos 9}

Ф d ^{( R ,9,}t ) =----- 7^ ^{e   ,                 (20)}

2R фр (R, 9, t) = 3aEE--------e-к(R-a) cos 9e-i“t, (21) 2 1 + — кa

ε '

3 c ( R , 9 , t ) = - c о ^f—J ф р ( R , 9 , t ) .

Допущение 3 . Малость числа Духина ^e exp ^d

I 2 kT J

Du ®-------- - ^ 1. Здесь Т d — штерновский

κa потенциал. Приведенные выше выкладки справедливы при отсутствии у частицы поверхностного заряда, наличие которого, согласно [10], вызывает необходимость учета эффектов, связанных с поверхностной проводимостью и концентрационной поляризацией. Для частиц с тонким двойным слоем относительный вклад этих эффектов характеризуется величиной числа Du. Отсюда следует, что при условии тонкого двойного слоя поляриза-e Т, цию слабо заряженных частиц, т.е. когда d^^ < 1, можно не только качественно, но и количественно описывать как поляризацию незаряженных частиц [10]. В связи с этим предложенная в [5, 6] теория в случае частиц с тонким двойным слоем пригодна для описания не только незаряженных, но и также слабо заряженных частиц, отвечающих условию Du < 1.

При этом найденное распределение ф _р ( R, 6 ,t ) и разностной концентрации ионов 5 c ( R,6,t ) в пределах двойного слоя необходимо изменить на величину сферически симметричных добавок Т ( R ) и 5c 0 ( R ) , характеризующих распределение соответственно потенциала и концентрации объемного заряда в равновесном двойном слое [5, с. 166]; [6].

Кроме поляризации диэлектрических частиц, в [5, § 5.1.2] рассмотрен также случай поляризации идеально поляризуемой частицы. Техника решения этой задачи идентична технике, приведенной выше. Отличия состоят лишь в граничных условиях.

Отметим в заключение этого раздела, что до сих пор рассматривались только линейные модели, при которых не должно создаваться эффекта возникновения стационарных течений.

Стационарные поляризационные течения, вызванные переменным электрическим полем.

Диэлектрическая частица в проводящей жидкости [5, § 5.2]; [6]

Электроосмотическое скольжение жидкости по поверхности частицы вызвано действием тангенциальной составляющей электрического поля на распределенные в подвижной части двойного слоя электрические заряды. При тонком двойном слое к а ^ 1 полагается, что скорость жидкости на поверхности частицы совпадает со скоростью электроосмотического обтекания этой частицы.

Допущение 4 [5, с. 170]; [6]

Изменение скорости электроосмоса по поверхности частицы за счет выделения в диффузном слое двойного слоя при к а ^ 1 поляризационных зарядов формально можно учесть с помощью добавки в формуле Смолуховского к равновесному Z -потенциалу величины ф Р = ф _р ( а, 6 ,t ) , действительной составляющей выражения (21) для скачка потенциала (21) в точке R = а : ф _р ( R, 6 ,t )| , вызванного поляризацией двойного слоя

3 aE 1     1

ф„ =--cos 6 cos to t .

p 2       ε

1 +— к а ε '

Кроме того, меняется и значение электрического поля, вызывающего движение: кроме тангенциальной составляющей поля E ₁ , добавляется тангенциальная составляющая электрического поля, вызванного скачком потенциала поля ϕ _d . В результате тангенциальная составляющая скорости жидкости при R = а равна [5, с. 171]; [6]

^V.\R = а

В (, + ф0 )д(Фо + Фd )

4пп      Р    ад6

R = а

Здесь ϕ ⁰ _p определяется из (23):

Ф 0 ( R = а , 6 , t ) = - аЕ 1 cos 6 cos to t .       (25)

Фл определяется в (20) при R = а и с заменой экспоненты ее действительной частью a3 E1 cosθ

Фа (а,6,t) =--2--о2-costot = aE1

--cos 6 cos to t .

Радиальная компонента скорости на поверхности частицы равна нулю

^V4 = а = ^0.

На бесконечности для радиальной скорости ставится краевое условие

V I = U = ^sZ Ee-^ltot R I R ^»      ⁰ 4 nn ¹ "

Для описания осесимметричных в данном случае течений в окрестности частицы решается система уравнений (7), (8), (24), (27), (28). Для этого в [5, 6] используется функция тока Ф (3). Согласно [5, 6], решение (как отмечает автор, линейной задачи) ищется в виде

Ф ( r, 9 ,t ) = Ф о ( r, 9 ,t ) + Ф p ( r, 9 ,t ) ,     (29)

где Ф 0 ( r,9,t ) соответствует решению задачи об электрофорезе в переменном электрическом поле без учета поляризации двойного слоя и соответствует члену Ф ₀ в разложении (5), который раскрыт в [5, с. 119] и представляет собой периодическую функцию времени с частотой to ; Ф _p ( r, 9 ,t ) — искомая добавка к решению, обусловленная только поляризацией частицы. Функция Ф _p ( r, 9 ,t ) ищется в [5, 6] в виде

Фp (r,9,t) = Фa (r,9) + Фt (r,9,t), (30)

где Ф a ( r, 9 ) = (ф _p ( r, 9 ,t )^| , где ( )[ означает осреднение по времени.

В [5, с. 172, 173]; [6] приведены окончательные уравнения и граничные условия для определения функции тока Ф _а , а также связанной с ней скорости течения:

E 4 Ф а = 0 ,                          (31)

Ф I a lr =1

Ф a

= 0,

5Ф a д r

- а sin² 9 cos 9 .

Решение системы (31)–(33) имеет вид [5, с. 173]; [6]:

а Г 1 i

Ф„ ( r, 9 ) =-- 1 — у sin ² 9 cos 9 ,

aV ’      2 V r2 J и соответственно для компонент скорости:

V ( r, 9 ) = -

^—— ( 1 --y)(3sin² 9 - 1) , 2 V r ²J^{V            1}

Аналогичные результаты получены в [5, 6] и для идеально поляризуемых сферических частиц. В [5, 6] приведены различия в решениях для этих двух случаев, на которых здесь не останавливаемся.

Замечания по поводу приведенных в [5, 6] результатов, полученных для нелинейных поляризационных течений

Остановимся на некоторых замечаниях к изложенным выше результатам, касающимся поляризационных течений.

Во-первых, изначально автором рассматривается линейная (как он сам утверждает в [6, с. 363]) задача (7), (8), (24), (27) и (28) (нумерация соответствует настоящей работе). После чего делается вывод о наличии возможности искать ее решение в виде суммы периодической функции времени с частотой ω , совпадающей с частотой внешнего электрического поля, и не зависящей от времени функции (см. выражения (29), (30)). Однако известно, что в линейной задаче при наличии периодического по времени источника невозможно получение апериодического решения.

Во-вторых, автор рассматривает линейную однородную систему уравнений движения Навье— Стокса (7), (8). Однако краевое условие (24) по умолчанию предполагает нелинейность задачи в силу того, что, несмотря на наличие исходного поля частотой ω , явочным порядком появляются постоянная составляющая to = 0 и кратная частота 2 ω . Поэтому для справедливости утверждения о линейности рассматриваемой задачи необходимо сторонний источник характеризовать краевыми условиями (24)–(28).

В-третьих, если рассмотреть краевое условие (24), то выясняется неотмеченное автором [5, 6] еще одно качество получаемого решения. А именно: разложим краевое условие (24) на слагаемые

V . L = а

ε

-----X

4 πη a

X Z

V

( ^д ^ 0 ₊ ^dV d )

V д 9   д 9 J

⁺ Ф ⁰

Г дФ0 + дФd ))V д9   д9 JJ

Учитывая выражения для ϕ ⁰ _p (23), ϕ ₀ (25) и ϕ _d (26), а также что Z = const, делаем вывод о том,