Электрохимическая обработка металлов неподвижным катодом-инструментом

Электрохимическая обработка металлов является эффективным и перспективным методом изготовления деталей различных устройств. Электрохимическое формообразование основано на явлении анодного растворения металла [1].

В работе рассматривается двумерная задача расчета формы обрабатываемой поверхности (анода), получающейся при электрохимической обработке неподвижным катодом-инструментом заданной формы. В процессе обработки анодная плотность тока j _a на обрабатываемой поверхности достигает предельного значения j _np , при котором происходит прекращение обработки, и конфигурация межэлектродной области не меняется с течением времени [1; 2].

Описание электродных процессов при электрохимической обработке представлено в монографии [1]. Установлено, что в процессе обработки неподвижным катодом-инструментом обрабатываемая поверхность покрывается слоем продуктов электрохимических реакций, происходящих в межэлектродном промежутке. Увеличение анодного потенциала не приводит (или почти не приводит) к увеличению j_a ; оно компенсируется утолщением слоя продуктов реакций, осаждающихся на поверхности анода.

Миназетдинов Наиль Миргазиянович кандидат физико-математических наук, доцент, доцент кафедры информационных технологий и естественно-научных дисциплин, Российский новый университет, Москва. Сфера научных интересов: приложения методов теории струйных течений идеальной жидкости в задачах теории электрохимической обработки металлов. Автор 40 опубликованных научных работ. SPIN-код: 7544-6638, AuthorID: 198232.

Величина j _np зависит от свойств электролита, обрабатываемого материала, ряда других параметров и устанавливается экспериментально [1].

Кроме обрабатываемых участков на поверхности заготовки могут существовать необрабатываемые участки, на которых происходит снижение анодного тока до значений, недостаточных для осуществления анодного растворения металла, например, участки анода, удаленные от рабочей части катода [1; 2].

Постановка задачи и численно-аналитический метод ее решения

Рассмотрим двумерную задачу электрохимической обработки, состоящую в определении формы анодной границы при ее обработке неподвижным двугранным катодом-инструментом. Сечение катода координатной плоскостью Ox ₁ y ₁ представляет угол DCF (см. Рисунок 1, а ), угол при вершине C равен ап . Начало системы координат совпадает с вершиной C катода. Перед началом процесса электрохимической обработки граница заготовки детали представляется прямой D’F’ . Точки D , D’ и F , F’ являются бесконечно удаленными. Величина зазора между гранью катода DC и границей заготовки D’F’ равна S ₁ . Через межэлектродный промежуток осуществляется прокачка раствора электролита.

На поверхности анода существует обрабатываемый участок D’A (см. Рисунок 2, b ), здесь межэлектродные зазоры малы. В процессе обработки на обрабатываемой поверхности D'A устанавливается предельная плотность тока j „_p . На поверхности заготовки можно выделить необрабатываемый участок, представленный отрезком AF’ (см. Рисунок 2, b ), в точках которой из-за увеличения межэлектродных зазоров величина анодного тока недостаточна для осуществления анодного растворения металла [1].

Ордината точки A перехода с обрабатываемой части D’A анодной границы на участок AF’ равна S ₁ .

В работе применяется модель идеального процесса [1], в которой предполагается постоянство во времени и в межэлектродном пространстве свойств электролита и не учитываются особенности электродных процессов. Принятые допущения означают, что удельная электропроводность электролита к , выход по току B _т для реакций анодного растворения металла, E_a , E_c – потенциалы анода и катода соответственно в модели являются постоянными величинами.

В области G z^ ( z 1 = x 1 + iy 1 , i² =- 1 ) межэлектродного промежутка на основе допущений модели идеального процесса потенциал u электрического поля является гармонической функцией с условиями на границах анода и катода-инструмента:

Электрохимическая обработка металлов неподвижным катодом-инструментом

где U –напряжение [1].

U a = U - E a , U c =— E c ,

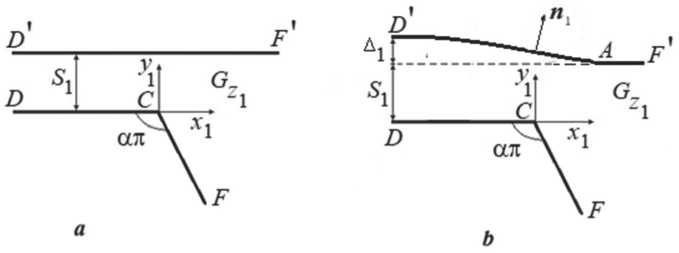
Рисунок 1. Геометрия межэлектродного промежутка:

а – до начала процесса обработки; b – получаемая в процессе обработки Источник: здесь и далее рисунки выполнены автором.

При постоянном напряжении U = U 0 время t k , необходимое для снятия припуска А 1 в сечении DD ’ межэлектродного промежутка (см. Рисунок 1, b ), можно определить по известной формуле [1]

_ ( 2 S i +А 1 ) А 1 t k =     2 D

где D = k_V x ( U 0 - E a + E c ) = k_V x ( u a - u c ) , k_V = B _T — -объем растворенного материала анода при прохождении 1 Кл электричества; s - электрохимический эквивалент металла; р -

плотность обрабатываемого материала.

Величину припуска А 1, _пр , при которой на анодной границе устанавливается предельная плотность тока, будем называть предельной.

Величину А 1, _пр и время t_k , „_р , необходимое для снятия предельного припуска, будем определять из условия, что на обработанной части заготовки выполняется равенство

j a    j np •

д и

Согласно закону Ома ja = к---, где n1 -вектор нормали к аноду (см. Рисунок 1, b), дп, тогда                              1

и„ — иг jnp = к~   c , где H = Si +А1,пр •

H

Из выражения (4) следует, что

H = к ^и u c j np

Таким образом, величина припуска А 1, _пр

•

и —и

А 1, пр = H — S i = к ^--^- — S i .

j np

Перейдем к безразмерным переменным:

z,       • x, У 1    . S л       ^А 1, пр      2 D,

Z — — = x + iy , x — — , y — ¹ , S — — , А =      , т = — -t ,

H        H H H ^пр H H ²

где t - время; т - безразмерное время.

Тогда безразмерную величину предельного припуска А „р и безразмерное время т _к , „р , необходимое для снятия припуска А _пр , можно определить по формулам

А _пр — 1 - S,

2D       2D (2S1 + А1,„р )А1,пр q- —_____4-     —__2______________L_______

^T k , ^пр   H ² tk , ^пр   H ²        2 D

— ( 2 S + А „р ) А „р — ( S + 1 ) А „р — 1 - S ² .

Введем аналитическую функцию W ( z ) — ^ ( x , y ) + i ^ ( x , y ) , где w — ( u - u c ) / ( u a - u c ) . Гармонические функции ф ( x , y ) и w ( x , y ) связаны между собой условиями Коши - Римана [2].

Рассмотрим задачу определения предельной формы границы D’A при выполнении сле- дующих условий для функции W (z) :

W d ' AF' ^{— 1} , W dCF ^— 0 .

dW dz

D ' A

д^ ~n~

= 1 .

D ' A

Область изменения G_w переменной W представлена на Рисунке 2, a .

Для построения функций, определяющих решение задачи, введем параметрическую комплексную переменную t = %+i6, изменяющуюся в области нок 2, b).

G t (I t |(1, $) 0 )

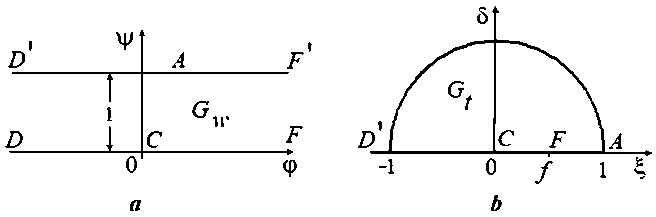
Рисунок 2. Вспомогательные области: а – область изменения комплексного потенциала W ; b – область изменения вспомогательной переменной t

Используя метод конформных отображений [3], получим dW_ (1 + f )2       (1 -1)

.

^{dt n}    (^{1 +} t )( t ^- f )(^{1 - tf} )

Введем функцию [4]

(см. Рису-

dW x (t) — In     — In dz

dW dz

^- i d ,

где и - угол между касательной к кривой и осью абсцисс в области G_z изменения переменной z .

Электрохимическая обработка металлов неподвижным катодом-инструментом

На границе области G t функция х ( t ) удовлетворяет условиям

Re x ( exp ( & ) ) = 0, <7 е[ о, п ]

Im x ( £ ) = - ^ ( £ ) =

0,

⁽ 1 ^{- а)п} ,

£ <-1;0)Ц f ;1 ] , £ ф; f ).

Функция % ( t ) имеет логарифмические особенности в точках C ( t = 0 ) и F ( t = f ) . Применяя метод особых точек Чаплыгина [4; 5], найдем

^{х (} t ^{)=( 1 -а} ) nt l t - ff )

Используя формулы (12), (15) и равенство dW dz = exp(-x(t)) —dt , установим соответствие между областями Gz и Gt при условии, что образ точки t (C) = 0 переходит в начало координат плоскости z. Это соответствие задается формулой

z _{( t} ) = ⁽¹ + ^f ) 2 f      ^{( 1 - т} y - d

п J ( 1 + т )( т - f ) ^{2 -а} ( 1 -к f ) ^а

Параметр f определяется из условия

Imz ( 1 ) = S .

Формулы (17), (18) позволяют определить форму предельной анодной границы для различных значений безразмерного начального зазора S .

Результаты расчетов

При а = 0,5 выполнен расчет безразмерных координат точек участка D'A предельной анодной границы для четырех различных значений величины S : 0,1; 0,3; 0.5; 0,7.

В таблице представлены результаты расчета безразмерных характеристик: x_A –аб-сциссы точки A , Л _пр , к п , _пр .

Таблица

Результаты расчета безразмерных характеристик

S	xA	Л пр	к к , Пр
0,1	1,146	0,9	0,99
0,3	1,006	0,7	0,91
0,5	0,817	0,5	0,75
0,7	0,545	0,3	0,51

Источник: таблица составлена автором.

Графики анодных границ для указанных частных случаев представлены на Рисунке 3.

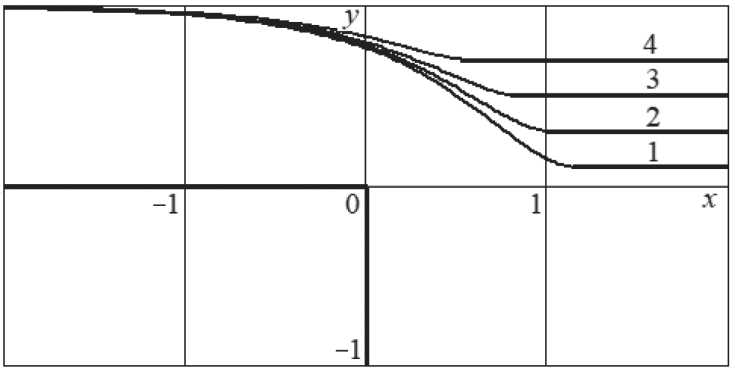
Рисунок 3. Результаты расчета анодных границ: 1) S =0,1; 2) S =0,3; 3) S =0,5; 4) S =0,7 Заключение

Решена конкретная двумерная задача, связанная с определением предельной анодной границы. Выполнены расчеты координат точек искомой границы и времени ее обработки для различных значений начального межэлектродного зазора. Из представленных результатов следует, что вследствие увеличения начального межэлектродного зазора происходит уменьшение величины предельного припуска и, соответственно, времени обработки.