Электрокалорический и барокалорический эффект в некоторых сегнетоэлектрических гидросульфатах и триглицинсульфате

В последние годы гигантский калорический отклик, обнаруженный в некоторых ферромагнетиках [1] и сегнетоэлектриках [2], стимулировал фундаментальные и прикладные интересы в разработке материалов, которые являются полезными для магнето-электрического охлаждения. БКЭ не было изучено в твердых телах так широко и интенсивно, как, например, ЭКЭ и МКЭ. Однако это свойство является очень привлекательным из-за своей общности для материалов любой физической природы (сегнетоэлектрик, ферромагнетик, сегнетоэластик и т. д.). Действительно, согласно соотношению Максвелла

(dSA ) = -(d%r) , (1) dpT , E, H ZT T'p, E, H где p, E, H – гидростатическое давление, электрическое и магнитное поле, соответственно, величина экстенсивного БКЭ ΔSBCE зависит от производной объема по температуре, которая, как известно, является самой большой вблизи точки фазового перехода.

Особый интерес представляет изучение возможностей различных калорических эффектов в одном и том же материале. Известно лишь несколько исследований, посвященных БКЭ и МКЭ в одном магнитном материале [3]. Что касается сегнетоэлектриков, их барокалорическая эффективность не изучалась до сих пор.

Попытаемся проанализировать ЭКЭ и БКЭ в ряде кристаллов Rb x (NH 4 ) 1– x HSO 4 , испытывающие, в зависимости от x , следующие последовательности фазовых переходов: P 2₁ /c → P c→ P –1 (x = 0, 0,02, 0,04) и P 2 1 /c → Pc (x = 0,33, 1) [4–6].

Кроме того, было интересно сравнить БКЭ с ЭКЭ в гидросульфатах, а также в триглицинсульфате (ТГС), который характеризуется довольно большим значением изменения энтропии при фазовом переходе Δ S = 6,8 Дж/моль·K [7] по сравнению с Rb x (NH 4 ) 1– x HSO 4 (Δ S ≤ 1,7 Дж/моль·K) [4-6].

Для выполнения поставленных задач, мы проанализировали данные по теплоемкости, диэлектрической проницаемости, интенсивном ЭКЭ и барические коэффициенты для Rb x (NH 4 ) 1– x HSO 4 [4–6; 8; 9] и ТГС [7; 10–12].

Сначала мы рассмотрели избыточную теплоемкость Δ C_p ( T ) в рамках термодинамической теории Ландау. Согласно [13] из термодинамического потенциала для фазовых переходов второго рода

АФ = A T ( T - T_PT ) P ² + BP ⁴ + CP ⁶ - EP        (2)

при E = 0 можно получить уравнение

^А c p

- 2

T

2^B ² - 3 A_TC A TT

12С ,

+ -a^- ( Tpt - T ) . (3)

Было установлено, что во всех исследуемых кристаллах (Δ Cp / T )^–2( T ) является линейной функцией в довольно широком диапазоне температур Δ T _L ниже точки фазового перехода T PT (табл. 1). Используя данные по диэлектрической проницаемости, мы вычислили значения коэффициентов в (2). Можно видеть, что даже довольно небольшая добавка рубидия ( x = 0,33) в твердом растворе Rb x (NH 4 ) 1– x HSO 4 приводит к снижению Δ T L и увеличению значения N = ( B ²/3 A T · C · T PT )^1/2, которая характеризует близость фазового перехода к трикритической точке. Принимая во внимание небольшое влияние электрического поля на коэффициент A_T [12] был проведен анализ уравнения электрического состояния ∂ΔΦ/∂ P = 0, и поверхность «поляризация–темпера-тура–электрическое поле» ( P–T–E ) была построена. По аналогии с уравнением (1) можно записать соотношение Максвелла для сегнетоэлектриков:

(dSAF)   =(dAr)   .             (4)

\ / ^dE ) p , T \ / ^{d T} ) p , E

Таблица 1

Температура фазового перехода T_PT; температурный интервал A T L , связанный с уравнением (3); коэффициенты термодинамического потенциала A T , B, C (2); близость к трикритической точке N

Кристалл	T PT , К	Δ T L , К	A Т · 102, K–1	B , (Дж/моль)–1	C , (Дж/моль)–2	N
NH 4 HSO 4	271,7	190–271,7	3,0	8,9·10–3	2,3·10–4	0,12
Rb0.33(NH4)0.67HSO4	269	220–265	1,4	4,0·10–3	2,5·10–5	0,24
RbHSO 4	264,6	240–262	5,0	0,04	8,4·10–4	0,22
ТГС	322,3	310–321	0,18	5,7·10–6	1,4·10–9	0,12

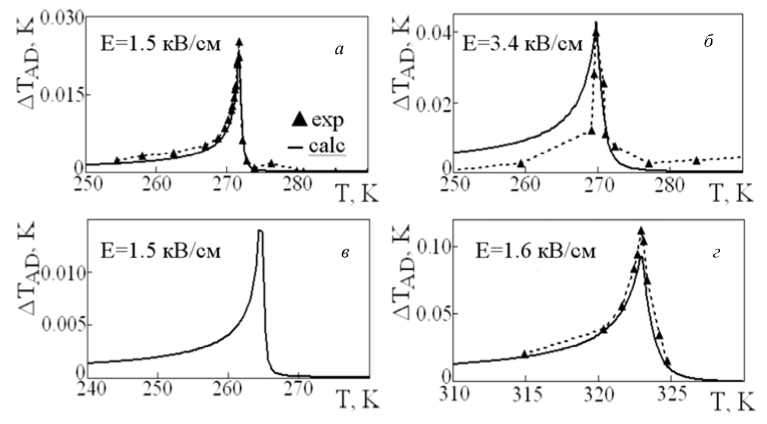
Рис. 1. Экспериментально измеренный и вычисленный интенсивный ЭКЭ Δ T_AD для NH₄HSO₄ ( a ), Rb 0.33 (NH 4 ) 0.67 HSO 4 ( б ), RbHSO 4 ( в ) и ТГС ( г )

Отсюда следует, что интенсивный электрокалори-ческий эффект может быть выражен как dT^E =-( T / Cp, E )(dP / dT ) p, e^E . (5)

По результатам рассмотрения уравнения электрического состояния были определены значения Δ T AD^ECE для твердых растворов Rb x (NH 4 ) 1–x HSO 4 (x = 0, 0,33, 1), а также для кристалла ТГС при электрических полях используемых в экспериментах [4; 10]. Было получено удовлетворительное согласие между вычисленными и экспериментально полученными значениями, а также их температурными зависимостями для всех исследуемых кристаллов (рис. 1). Максимальная величина Δ T AD^ECE в твердых растворах отличается друг от друга (при одном и том же E ) в соответствии со значением N , так как производная поляризации по температуре увеличивается с уменьшением N . Таким образом, полученные результаты доказывают возможность применения рассмотренного в статье метода для косвенного определения Δ T_AD ^EC на основании исследований теплоемкости и диэлектрической проницаемости.

Самым надежным способом для определения калорического эффекта является прямое измерение изменений температуры с помощью, например, адиабатического калориметра. На самом деле, этот способ относительно прост для изучения ЭКЭ и МКЭ [3; 4; 10]. Но для барокалорических измерений этот метод не удобен. Мы оценили барокалорическую эффективность исследуемых кристаллов в рамках приближения разработанного в [14].

Разрушение монокристалла NH 4 HSO 4 при сильном фазовом переходе первого рода Pc → P- 1 при T 2 препятствует изучению ЭКЭ. С другой стороны, довольно большие изменения энтропии Δ S 2 = 1,4 R и объема Δ V 2 / V ≈ 1,2 %, а также гигантский барический коэффициент dT ₂/ dp = 76,5 K/кбар делают этот переход весьма перспективным для исследования БКЭ (рис. 2).

Можно предположить, что существует ничтожно малый эффект довольно малого давления (p < 10 кбар) на решеточную теплоемкость CL и решеточную энтропию SL. Таким образом, суммарная энтропия S(p, T) при p > 0 может быть определена как сумма независящей от давления части SL = ∫(Cp/T)dT и аномального вклада ΔS2 = ∫(ΔCp/T)dT, определенного при p = 0 и смещенного по температурной шкале при p > 0 в соответствии со значением dT2/dp [1]. Полная энтропия в зависимости от температуры и давления показана на рис. 2, а. Значения экстенсивного БКЭ были вычислены как разность ∆SBCE(T, p) = S(T, p ≠ 0) - S(T, p = 0) при постоянной температуре (рис. 2, б). Очевидно, что значение на- сыщения ∆SBCE будет равно энтропии фазового перехода Pc → P–1, которое довольно велико ~ Rln4 в NH4HSO4 при T2 [5]. Интенсивный БКЭ ΔTADBCE был определен как изменение температуры при постоянной энтропии в зависимости от давления (рис. 2, в). Максимальное значение ΔTADBCE ≈ 19 K сопоставимо со значениями в ферромагнитных и сегнетоэлектрических материалах, которые рассматриваются как перспективные материалы в качестве твердых хладагентов [1; 2]. Самое главное, что давление, необходимое для обеспечения максимума БКЭ при T2 в NH4HSO4, является относительно низким р ≥ 0,3 кбар.

Используя вышеупомянутую процедуру, было определено адиабатическое изменение температуры с изменением давления в окрестности фазовых переходов второго рода в Rbx(NH4)1–xHSO4 и ТГС. Из-за ма- лой величины энтропии (ΔS < ln2) величина ΔTADBCE оказывается также незначительна (рис. 3). Видно, что замена Rb → NH4 приводит к сильному уменьшению значения ΔTADBCE. Самый низкий интенсивный БКЭ характерен для ТГС и связан с самым низким барическим коэффициентом dT/dp = 2,6 K/кбар. Сравниваются ЭКЭ и БКЭ (табл. 2). Для того чтобы значения обоих эффектов были близки в районе перехода P21/c → Pc в NH4HSO4, требуется очень низкое давление и большое электрическое поле. Сравнение полученных данных показывает также, что, с одной стороны, ЭКЭ является самым большим в ТГС и, с другой стороны, сульфат водорода характеризуется самой большой барокалорической эффективностью благодаря большому барическому коэффициенту dT1/dp = 14 K/кбар.

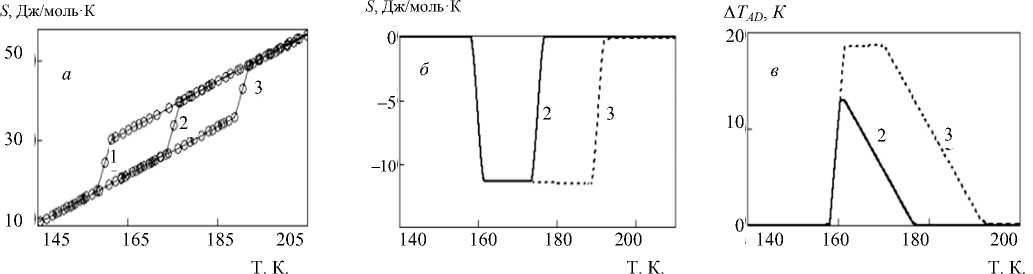
Рис. 2. Полная энтропия S ( a ), экстенсивный Δ S ( б ) и интенсивный Δ T_AD ( в ) БКЭ для NH₄HSO₄ в окрестности фазового перехода Pc → P– 1; p = 0 бар (1); p = 200 бар (2); p = 400 бар (3)

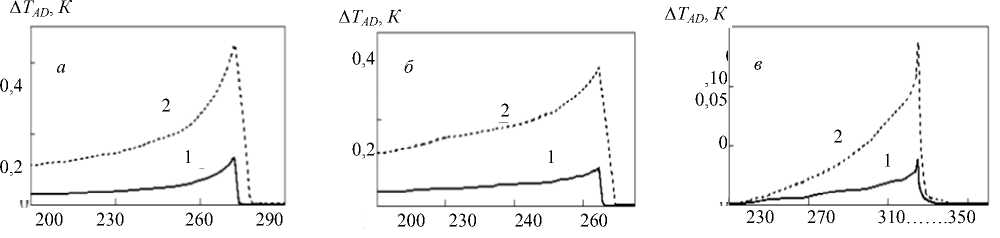
Т. К.                                               Т. К.                                               Т. К.

Рис. 3. Интенсивный Δ T AD БКЭ вблизи фазового перехода второго рода в NH 4 HSO 4 ( a ), RbHSO 4 ( б ) и ТГС ( в ); p = 100 бар (1), p = 400 бар (2)

Таблица 2

Температура фазового перехода T PT , электрическое поле E , гидростатическое давление р, интенсивный и экстенсивный ЭКЭ (A T _AD ^ECE , A S ^ECE ) и БКЭ (A T AD^SCE , A S ^BCE ). Данные по A T ADECE в ТГС [10]

Кристалл	T P T , К	Е , кВ/см	Δ T ADECE , K	Δ S ECE , Дж/кг·K	p , бар	Δ T ADBCE , К	Δ S BCE , Дж/кг·K
NH 4 HSO 4	271,	1,5	0,025	–0,11	20	0,027	–0,12
	160				20	1,3	–57,6
Rb 0.33 (NH 4 ) 0.67 HSO 4	269	1,5	0,025	–0,076
RbHSO 4	264,6	1,5	0,014	–0,044	20	0,02	–0,042
ТГС	323	1,6	0,112	–0,617	20	0,007	–0,044

Таким образом, анализ экспериментальных данных теплоемкости и диэлектрической проницаемости позволяет получить достоверную информацию, касающуюся электрокалорических эффектов в сегнетоэлектриках, испытывающих фазовый переход второго рода, близкий к трикритической точке. Сегнетоэлектрики, характеризующиеся довольно низкой энтропией фазового перехода и высокой восприимчивостью к гидростатическому давлению, могут показать значительную барокалорическую эффективность по сравнению с электрокалорической.