Электромагнитная модель и оптимизация параметров торцевого генератора

Примеры повышения эффективности НТСГ: увеличение сечения магнита при оптимальном его размещении в ограниченном пространстве; снижение пазового рассеяния.

Необходимость повышения единичной мощности микроГЭС (от 1-3 кВт до 20-30 кВт) и возможность использования на крутосклонных реках со скоростью течения до 3,5-5 м/с потребовали существенных изменений параметров:

• -    использование провода не только круглого, но и прямоугольного сечения вследствие повышения токов обмотки статора;

• -    увеличение высоты паза, приводящее к возрастанию пазового рассеяния, и поиску компромисса между радиальным габаритом генератора, массой магнитов и внешней характеристикой генератора;

• -    увеличение воздушного зазора, обусловленное технологическими погрешностями изготовления генератора, и нахождение оптимального соотношения: зазор – массы магнитов и обмоточного провода.

Конкурентоспособность изделий достигается многократным сокращением трудоемкости конструкторско-технологического проектирования использованием интегрированной компьютерной среды [2], предполагающей наличие математических моделей процессов, и использование средств их оптимизации. Торцевая синхронная машина представлена трехзонной моделью, включающей обмоточную структуру статора, воздушный зазор, постоянные магниты ротора. В основу модели положены уравнения магнитостатики [3] для любой зоны машины. Структура активного объема торцевой электрической машины, используемая для построения расчетной модели, представлена на рис. 1.Выражение для составляющей вектора магнитной индукции в воздушном зазоре (зона 3) расчетной модели, полученная из решений уравнений магнитостатики [4], имеет вид

B = Ц    = ц ^. f M • k ^ ch ^{k n}3 • sm^{k n} • x J =

2 У   °' d y   °' ^ t k т     т        т J

= С,   . sin^{k n} . x

2y     т где Мk – постоянные интегрирования, определяемые из условия непрерывности потенциала; τ - полюсное деление по среднему диаметру; 3 -величина воздушного зазора.

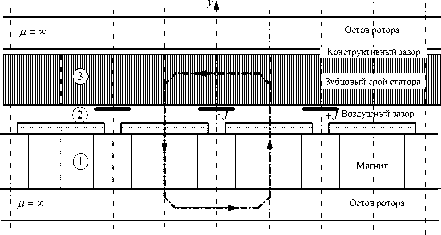
Рис. 1. Расчетная модель активной части генератора

Поле возбуждения В 2у , созданное магнитами ротора, и поле реакции якоря В 3у относительно неподвижны. Пространственно эти поля сдвинуты друг относительно друга на внутренний угол нагрузки Θ. Тогда поле реакции якоря этой же поверхности будет описываться выражением

В 3 у ( x , У ) = Х C з _У ^s in | — x + k ®\ ,       ⁽²⁾

у               y t т         J где С3у – постоянная интегрирования являющаяся функцией настила тока:

u псл I ф , t₁

где u псл – число проводников в пазу статора, t 1 – зубцовый шаг статора.

Полученное из уравнения, составленного по второму закону Кирхгофа, значение фазного тока статора с учетом (1) и (2) после преобразований имеет вид воздушного зазора, полюсного деления, размеров магнита. Так как числитель представляет собой ЭДС магнитного поля ротора, то синхронное индуктивное сопротивление равно:

xd = j • ®‘ WP • l8 т • иЯСл •(^ - X + Z)+ j • Хл то есть представляет собой сумму индуктивного сопротивления реакции якоря и пазового рассеяния.

Основной характеристикой синхронного генератора является внешней характеристики – зависимость выходного напряжения генератора от тока якоря при постоянной угловой скорости и характере нагрузки U = f ( I ) (при Ω=const, cos φ=const). Тогда используя выражение для фазного тока (3) можно записать:

Uj = - j - to • w^ • ]B 3y S -

^-f I ф • ^Г1 ⁺ I ф • ^j ' ^x л ⁺ I ф • ^j ' ^to • W P ■ 1 § ■^T•^u псл '^{( Y -} X ^{+ Z )}Jj ⁽⁵⁾

Электромеханическая мощность, развиваемая ротором синхронной машины с беспазо-вым статором, равна приращению действительной части потока вектора Пойнтинга при переходе через границу ротор – воздушный зазор, с учетом (1) и (2) выражение электромеханической мощности примет вид:

b*

P = 2 pl g v Re Jp g u _псл I, • ( / - X + Z ) sin ( 0 ) • Hdx ;  ⁽⁶⁾

0         ф

Используя это выражение, можно аналитичес-ки рассчитать угловую характеристику мощности PH при различных значениях угла Θ, проанализировать влияние геометрических параметров на перегрузочную способность генератора. Расчетная модель генератора позволяет сформировать поток данных, необходимых для его проектирования и конструирования:

• -    энергетические характеристики (мощность, КПД, напряжение, ток статорной обмотки);

• -    массогабаритные показатели, необходимые для производителя и потребителя машины (массы электротехнической стали, обмоточной меди, магнитов, общая масса машины, ее габаритные размеры);

Расчетная модель в сочетании с инструментами многокритериальной оптимизации позволяет создать программный комплекс проектирования синхронного генератора, являющийся компонентом интегрированной среды проектирования, исследования, подготовки производства свободнопоточных микроГЭС и их существенного компонента – торцевых синхронных генераторов. В настоящее время принципы решения задач многокритериальной оптимизации сводятся к следующим этапам:

• -    разработка целевой функции качества системы;

• -    формулирование критериальных ограничений;

• -    выбор из созданного множества точек Па-ретто варианта, удовлетворяющего критериальным ограничениям с сортировкой точек по степени приближения к оптимальному результату.

В программном модуле предоставлена возможность комбинировать в любых сочетаниях методы оптимизации, предварительно определив:

• -    непрерывные диапазоны их изменений min       max

ai ≤ α i ≤ ai ,            (11)

где α i – варьируемый параметр; α i ^min , α i ^max – начало и конец диапазона;

• -    необходимое количество функциональных ограничений в виде:

g ⁽ x 0 , . , x k ) ^ ⁰ ,         (12)

где g(x0,.,xk) - функция нескольких пере менных.

• -    критериальные ограничения системы (критерии качества), их минимальные и/или максимальные значения в виде:

где f ( x ₀. „. x _n) - функция заданная аналитическим выражением, k – максимальное (минимальное) значения критерия,.

Для поиска оптимального варианта сочетания параметров машины использован метод многокритериальной оптимизации параметров Соболя-Статникова [4], который не требует сведения многокритериальной задачи к однокритериальной, что исключает неоправданное упрощение задачи, а также позволяет учесть опыт конструктора, определяя множество с минимальным количеством решений, удовлетворяющее заданным условиям. Входной поток для алгоритма оптимизации – коллекция работоспособных вариантов машин в виде совокупностей их параметров, полученных в результате использования расчетной модели генератора и перечисленных выше. Варьируемыми параметрами для синтеза коллекции являются: внутренний активный диаметр, активная длина машины, воздушный зазор, индукция в зазоре машины, плотность тока в обмотке статора. Критериальные ограничения приняты по аналогии с ранее испытанными образцами генераторов и исходя их конструктивных условий [5]. Критериями качества генератора выбраны следующие характеристики: номинальное напряжение, величина перегрузочной способности, суммарная масса генератора, масса магнитов, наружный диаметр генератора, индуктивное сопротивление пазового рассеяния.

По этим принципам реализован программный модуль, обладающий следующей функциональностью: формирование исходной коллекции решений в заданной области изменений варьируемых параметров, усечение (ранжирование) исходной коллекции по заданным значениям критериев качества, вычисление значений целевой функции по приоритетам значимости критериев и определение оптимального варианта (рис. 2). Также предусмотрена возможность использования аппарата ЛП-последовательностей, применяемых для обхода многомерного пространства параметров, альтернативного равномерному распределению точек решений.

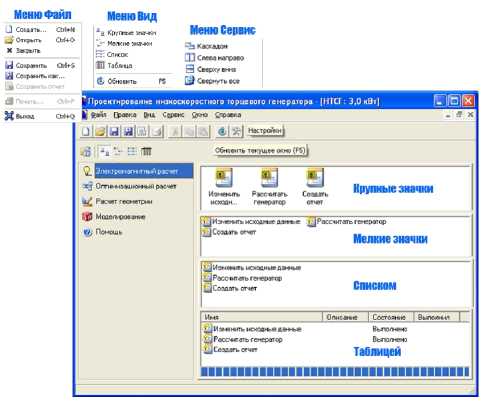
Рис. 1. Основные элементы интерфейса программы NTSGen

Количество точек ЛП-последовательности определяется по формуле:

c = L ma^ ,                     (14)

p где Lmax – длина наибольшего диапазона значения параметра; p – шаг разбиения наибольшего диапазона, определяющий общее количество точек, а значит точность решения задачи.

Общее количество точек:

k = (nc div 1)n

где n – количество параметров; с – количество точек (14).

Количество отрезков в сетке для одного измерения определяется так:

d =

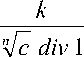
где k – общее количество точек (15); n – количество параметров; с – количество точек ЛП-последовательности (14). Значение параметра для одного решения:

k

= a +

b - a d

• z ,

где а – начало диапазона, b – конец диапазона, d – число определяется по (16), z – случайное число, обеспечивающее уникальных значений параметров.

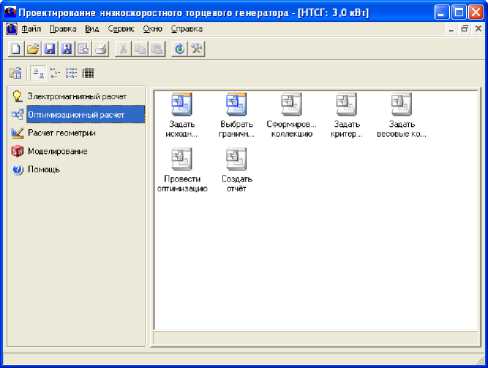
Рис. 3. Ввод исходных данных и граничных условий

приоритета критерия, MIN – минимальное значение i- го критерия. Интерфейс отвечает требованиям Windows-стандартов. Программа имеет модульную структуру и отвечает требованиям структурного программирования, в частности, весь основной функционал оформлен в виде подпрограмм, которые можно использовать в дальнейшем при решении задач оптимизации, никак не привязанных к текущим.

На первом этапе пользователь устанавливает значения параметрических ограничений. Программа автоматически формирует множество решений, удовлетворяющих заданным ограничениям. На втором этапе, основываясь на коллекции допустимых решений, пользователь (конструктор) назначает диапазоны изменения критериев качества и приоритеты, которые устанавливают весомость каждого из критериев. При этом по умолчанию в качестве диапазонов изменения критериев качества из банка готовых решений выбираются максимальные и минимальные значения всех критериев (рис. 3). При равенстве приоритетов реализуется поиск компромисса. Так как критерии качества зачастую противоречат друг другу, пользователь должен установить критериальные ограничения. Далее программа автоматически выполняет проверку полученного множества на непустоту. При положительном результате проверки на выходе получается ранжированная коллекция, ранжирование которой можно повторить, назначая более строгие ограничения.

При определении коэффициента оптимальности точки по критерию, который должен стремится к максимуму или минимуму, используются формулы:

R = D MAX i - C ■ , R = D • C i ^- MIN . .

ⁱ ' MAX . - MIN i ' ' MAX. - MIN.

В (19) и (20) MAX , MIN – максимальное или минимальное значение i- го критерия, С_i – значение i- го критерия точки, D i – значение

Таблица 1. Выходные параметры генератора

Выходные параметры	Много-крите-риаль-ная оп-тимиза-ция	Одно-нофак факторный ана лиз	% откло кло-нения
индукция в воздушном зазоре, Тл	0,68	0,7	-2,9
активный диаметр, м	0,632	0,67	-6,01
активная длина, м	0,02	0,021	-5
напряжение, В	238,32	218,21	8,44
максимальная мощность, Вт	6451	5864	9,1
масса генератора, кг	36,235	40,26	-11,1
масса магнитов, кг	1,226	1,326	-8,16
индуктивное сопротивление, Ом	4,245	5,224	-23,06

В качестве примера, иллюстрирующего возможности предлагаемых моделей и методов, использован генератор мощностью 3 кВт с числом полюсов 24. Здесь метод многокритериальной оптимизации позволил значительно улучшить выходные параметры генератора по сравнению с использованной ранее методикой однофакторного анализа (табл. 1).

Применение метода многокритериальной оптимизации позволило снизить (знак минус) массу дорогостоящих магнитов на 7,6% и суммарную массу генератора на 7,4%, а также увеличить (знак плюс) энергетические показатели машины на 8,4% за счет снижения влияния сопротивления пазового рассеяния. Алгоритмы, разработанные на основе методик электромагнитного расчета и многокритериальной оптимизации, реализованы в виде программного комплекса, который позволяет автоматизировать твердотельное моделирование в CAD -среде, сокращая сроки разработки изделия от технического задания до комплекта рабочей документации. В состав программного компонента интегрированной среды проектирования свободнопоточной микроГЭС, кроме описанных в статье алгоритмов, будут на следующем этапе включены модули анализа отказоустойчивости наиболее нагруженных элементов генератора: жесткость диска остова статора и ротора, сопряженного с валом, долговечность подшипников ротора и др.

Выводы: созданный коллективом авторов инструментарий автоматизированной разработки микроГЭС, опыт их проектирования и испытаний позволили перейти к сертификации изделий и технологической подготовки промышленного производства.