Электромагнитная связанность композита "пьезоэлектрик/феррит" с начальным напряженным состоянием

ВЕСТНИК ПНИПУ. МЕХАНИКА № 4, 2022PNRPU MECHANICS BULLETIN

Изучение закономерностей и эффектов влияния начального напряженного состояния элементов структуры материала на особенности его последующего нагружения – одна из задач механики композитов [1–9]. Решение этой задачи актуально для различных практических приложений, в частности, ультразвукового неразрушающего контроля напряженного состояния нагруженных конструкций [10], методов геомеханики и сейсмических исследований [11]. Математическое моделирование и численное решение этой задачи возможно с использованием «линеаризованного подхода» на основе линеаризованных уравнений теории упругости для тела с начальным напряженным состоянием [3; 6; 7; 12; 13]. С использованием этого подхода получены численные решения и осуществлен дисперсионный анализ распространения упругих волн в композитах (конструкциях) с учетом наличия начального напряженного состояния, в частности, осуществлен анализ скорости распространения поверхностных волн в однородном слое на предварительно напряженном неоднородном полупространстве [14], анализ влияния величины начального бокового давления на поверхности полого составного цилиндра на скорость распространения осесимметричной волны [15], анализ влияния величины начального напряженно- го состояния ортотропной композитной пластины с двумя близко расположенными параллельными цилиндрическими (туннельными) полостями с прямоугольным поперечным сечением на свободные и вынужденные колебания [16]. Для упругих композитов с идеально периодическими начально-напряженными структурами известны асимптотические решения, в частности, когда начальное напряженное состояние слоистой или однонаправленно-волокнистой структуры обусловлено тепловым нагревом [17].

Магнитоэлектрические материалы являются одними из наиболее перспективных функциональных материалов современной электроники [18–25]. В них сочетаются уникальные упругие и электромагнитные (в частности, диэлектрические, пьезоэлектрические, магнитострикционные) свойства, которыми можно эффективно управлять с помощью внешних механических и электромагнитных воздействий. Магнитоэлектрические константы гомогенных магнитоэлектриков очень малы, что обусловливает создание гетерогенных композиционных магнитоэлектриков, магнитоэлектрические константы которых могут на несколько порядков превосходить соответствующие константы гомогенных материалов [24]. Возникновение эффекта магнитоэлектрической связанности композита обусловлено деформационным взаимодействием его пьезоэлектрической и магнитострикцион- ной подсистем (фаз) даже в отсутствие такого эффекта для каждой фазы. Теоретическое изучение закономерностей влияния различных структурных параметров на электромагнитные поля (на микро- и макроуровнях) и эффективные (на макроуровне) электромагнитные и термоупругие свойства таких композитов основываются на постановке и решении связанных краевых задач элек-тромагнитотермоупругости для микронеоднородной представительной области с использованием методов механики композитов [26–32], в частности, асимптотических «методов осреднения» [21; 23; 26] и методов на основе двоякопериодических комплексных функций [27] для идеально периодических структур, методов статистической механики композитов для нерегулярных, в частности, полидисперсных (рис. 1, а, b) и квазипериоди-ческих (рис. 1, с, d) структур [28–32], численных методов (пакетов прикладных программ) решения задач на ячейке периодичности или реализациях представительного фрагмента случайной структуры [30]. При этом для по-лидисперсных структур (рис. 1, а, b) решения для тензоров эффективных термоупругих и электромагнитных свойств получены в аналитическом виде [28; 32–35]. В [24; 25; 33] исследована максвелл-вагнеровская релаксация композитов «феррит/пьезоэлектрик», даны концентрационные и частотные зависимости действительных и мнимых частей эффективных электромагнитных констант. В [33–35] исследованы эффективные электромагнитоупругие свойства полидисперсных структур на основе аналитических решений. Линеаризованный подход теории упругости для тела с начальным напряженным состоянием обобщен на магнитоэлектроупругий композит [36]. Численный анализ динамического поведения пьезоэлектрических композитов с учетом начального электроупругого напряженного состояния фаз дан в [37]. Актуальным остается нахождение решений связанных краевых задач механики пьезоактивных композитов с комплексным учетом структурных особенностей, в частности, статистического характера взаимного расположения элементов структуры, взаимодействия возникающих в них связанных электрических, магнитных и деформационных полей и наличием начального деформационного, электрического и магнитного напряженного состояния.

Цель – изучение влияния начального (микро- и мак-роуровневого) напряженного состояния на эффективные свойства композита с квазипериодической структурой (см. рис. 1, c , d ) из пьезоэлектрических и магнитострикционных фаз в рамках обобщенного сингулярного приближения статистической механики композитов [29; 38]. Квазипериодические модели структур композитов позволяют непосредственно учитывать разупорядоченность элементов структуры, например, связанную с технологией их изготовления через вычисление поправок к известным решениям для идеально периодических структур [30].

1.    Постановка задачи

Модели структур композитов . Рассматриваем две матричные квазипериодические двухфазные однонаправленные волокнистые структуры «со смещением» волокон (см. рис. 1, c ) и «с удалением» волокон (см. рис. 1, d ) в периодических гексагональных ячейках в трансверсальной плоскости r ₁ r ₂. В первой модели (см. рис. 1, c ) центры круговых поперечных сечений волокон имеют независимые для каждой гексагональной ячейки случайные смещения a из центров своих ячеек в плоскости r 1 r 2 ; сечения не выходят за пределы ячеек. Ориентационный угол и модуль вектора отклонений a распределены по независимым равномерным законам на отрезках [0; 2π] и [0; Δ ] соответственно, где Δ= k Δ _max, k ∈ [0; 1] – степень разупорядоченности волокон, Δ= R - r (1 +δ /2) – величина максимально max          υ 0

допустимого смещения, R – радиус вписанной в ячейку окружности, r _υ – радиус поперечных сечений волокон, δ ₀ ≡Δ ₀/ r _υ = 0,02 – относительная величина минимальной гарантированной прослойки Δ ₀ матрицы между волокнами. Во второй модели (см. рис. 1, d ) имеем статистически независимые для различных ячеек случайные размещения центров поперечных сечений

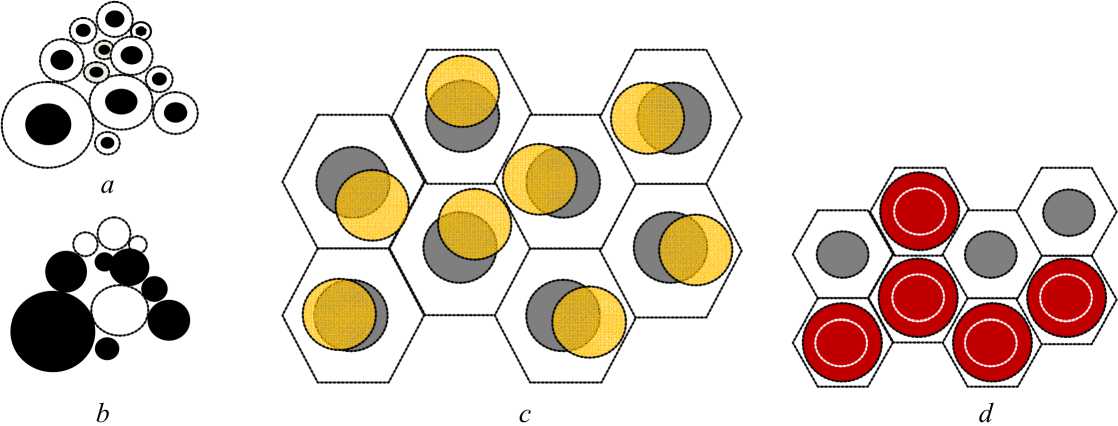
Рис. 1. Фрагменты реализаций полидисперсных ( а , b ) и квазипериодических ( c , d ) структур

Fig. 1. Fragments of implementations of polydisperse ( a , b ) and quasi-periodic ( c , d ) structures

волокон в центрах ячеек при заданной минимальной гарантированной прослойке А ₀ матрицы между волокнами также 2 % от r _y . Введем в рассмотрение две вспомогательные «базовые» структуры: первая – это периодическая структура (решение для которой считаем известным), вторая – «статистическая смесь» в виде полидисперсной «кластерной» структуры на рис. 1, b , из однотипных (по форме и ориентации) однородных полидисперсных (в том числе бесконечно малых) частиц, в которых статистически независимо реализуются с вероятностью v ₁ свойства 1-й фазы и с вероятностью 1– v ₁ – свойства 2-й фазы; представительный объем представляет собой два взаимопроникающих кластера частиц каждой из фаз (см. рис. 1, b ). Для статистической смеси отсутствует корреляция свойств в ее различных точках и, как следствие, имеем предельную локальность ее многоточечных моментных функций структуры [29–32].

Математическая постановка задачи. Пусть представительная область V композита, например, с квази-периодической двухфазной структурой (см. рис. 1, c, d) состоит из однородных трансверсально-изотропных пьезоэлектромагнитных фаз, плоскости изотропии которых лежат в координатной плоскости r1r2, ось поля- ризации r3 . Взаимное расположение фаз в области V задаем через их индикаторные функции if (r), для ко- торых имеем if = 1 если r е Vf , if = 0 если r g Vf,

F где Vf - область f -й фазы в V = ^ Vf , f = 1, F , здесь f=1

число фаз F = 2 (в общем, F > 2).

В области V композита имеем некоторое начальное равновесное электромагнитоупругое состояние Z0 = {о0, D0, B0} в виде полей начальных механических напряжений σ0 , электрической D0 и магнитной B0 индукций, которые обусловлены действием на композит некоторых начальных внешних механических нагрузок [1–17] и/или электромагнитных полей [36; 37]. Осредненные (макроскопические) значения – Z0 =< Z0 > , где < ... >= 1/V| ...dr — оператор осреднения по области V. Значение ζ*0 = 0 имеем для случая наличия самоуравновешенных остаточных напряжений σ0 и индукций D0 , B0 внутри области V после ее раз- грузки на макроуровне. Начальные поля σ0 , D0 , B0 удовлетворяют уравнениям равновесия о0 . = 0 и непрерывности D0 = 0, B” i = 0 .

При последующем (дополнительном к начальному) электромеханическом нагружении области V композита дополнительно возникающие в V поля напряжений σ и индукций D , B удовлетворяют уравнениям равновесия [1; 17] и непрерывности [36; 37] вида

(о +° X k ) j = ⁰ , ⁽ D ⁺ D 0 u , k У, = ⁰,

( B j + B U jk ) , j = 0                 (1)

с учетом поправок (дополнительных слагаемых), обусловленных наличием заданных начальных полей σ0 , D0 , B0 и дополнительного искомого поля перемещений u. Первое уравнение в (1) может быть преобразовано к виду о, j+° 0u, kj =0

с учетом выполнения уравнений равновесия G ° _kj j = 0 для поля σ ⁰ . В (1) напряжения σ и индукции D , B выражаются по известным определяющим соотношениям [20–22, 31, 32]

° ij = C ijmn u m , n — e nij E n — ^hmj^Hn — P ij ⁰ ’

D -e и + X. E + л 0,          (2)

iimnm , ninni ^,

В =h и H + »0 imn m, n ^ in n через градиенты перемещений Vu, напряженности электрического E и магнитного H полей, однородное приращение температуры 0 с использованием известных тензоров упругих свойств C f , пьезоэлектрических ef и пьезомагнитных (магнитострикционных) hf свойств, диэлектрических λ f и магнитных μ f проницаемостей, температурных коэффициентов β f , пироэлектрических пf и пиромагнитных Af постоянных для каждой фазы f. Компоненты тензора деформаций eij = (ui j + Uj i) / 2 , векторов напряженностей Ei = - ф i, Hi = - у i вычисляются через поля перемещений u = u(r), электрического ф = ф(г) и магнитного у = у(г) потенциалов с граничными условиями

• ^и^ = ^иХ ф г = - e , * r ; , у г =— в * r ^ ,     (3)

где r еГ - граница области V , осредненные или макроскопические значения напряжений о * =< о >  , градиентов перемещений u * =< V u >  , напряженностей электрического E =< E >  и магнитного H * =< H >  полей для области V . Решение задачи (1)–(3) сводится к нахождению пульсаций u '( r ) = u ( r ) - u * ( r ) , ф '( r ) = ф ( г ) -ф * ( г ), у '( г ) = у ( г ) -у * ( г ) - отклонений искомых полей перемещений u ( r ), электрического ф ( г ) и магнитного y ( r ) потенциалов от соответствующих полей макроскопических (осредненных) значений U i = U *^ , ф * =- E i * r , у * = - B i * r i с учетом выполнения граничных условий

• (3) . Поля пульсаций u '( r ) , ϕ '( r ) , ψ '( r ) пропорциональ-

• ***

ны заданным макроскопическим значениям ε , E , H , Θ и, как следствие, представимы в виде разложений ui'(r) =aimn(ζ0,r)um*n+bin(ζ0,r)En*+ +din(ζ0,r)Hn*+ti(ζ0,r)Θ,

• -ϕ'(r)=fm⁽¹n⁾(ζ0,r)um^*n+hn⁽¹⁾(ζ0,r)En^*+           ₄

2.    Метод функций Грина

+ m n ⁽¹⁾ ( ζ 0 , r ) H n ^* + t ⁽¹⁾ ( ζ 0 , r ) Θ ,                 ^{( )}

-ψ'(r)=fm(n2)(ζ0,r)u*mn+hn(2)(ζ0,r)En*+ +mn(2) (ζ0, r)Hn*+t(2) (ζ0, r)Θ с зависимостью коэффициентов разложений от начального напряженного состояния ζ0 композита.

Используем функции Грина

G =

^U ik Φ _k Ψ k

_Ui (1)    _Ui (2)

_Φ (1)   _Φ (2)

_Ψ (1) _Ψ (2)

G = G ( ρ ), ρ = r - r ₁

однородной трансверсально-изотропной пьезоэлектромагнитной «среды сравнения» [29] для интегральной формы записи коэффициентов разложений a ( r ), f ⁽¹⁾( r ), …, t ⁽²⁾ ( r ) (4) [31; 32; 38]. Например, запишем первые члены ряда коэффициентов пульсаций перемещений

'

imn 0^,                 ij , s 1 jsmn 1

+ U i ⁽,¹ s ⁾ ( r - r 1 )( e s ^' mn ( r 1 ) +δ sm D n ^0' ( r 1 )) +

+Ui(,2s)(r-r1)(hs'mn(r1)+δsmBn0'(r1))]dr1+..., bin (Z0 , r) = J [-Uy,s (F - Fl )enjs (r1 ) +

+Ui(,1s)(r-r1)λ'sn(r1)]dr1+..., din (Z0 , Г) = J [-Uj,s (F - Fl )hnjs (rl ) +

+U

+Ui(,2s)(r-r1)ϑ's(r1)]dr1+..., коэффициентов пульсаций электрического потенциала fm )(Zo, r) = J [Фу, s (r - Fl) C'm. (Fl) +

+Φ,⁽s¹⁾(r-r1)(es^'mn(r1)+δsmDn^0'(r1))+

+Φ,(s2)(r-r1)(hs'mn(r1)+δsmBn0'(r1))]dr1+..., hn1’ (Z0 , r) = J [-ФЛ s (F - rl ) enjs (rl ) +          (7)

+Φ,(1s)(r-r1)λ'sn(r1)]dr1+..., m»’ (Z0 , r) = J [-Ф j,s (r - rl )hnjs (rl ) +

V

+Φ_,⁽_s²⁾(r-r₁)μ^'_sn(r₁)]dr₁+...,

t^(l)(Z0, r) = J ^[-Фj,s^(r- rl ^)ejs⁽rl ) ^+Ф(s^)(r- rl ⁾ⁿs⁽rl ) ⁺

+Φ,(s2)(r-r1)ϑ's(r1)]dr1+..., коэффициентов пульсаций магнитного потенциала fm 2)(Z0, r) = J [Tj,s (r - Fi) Cjsmn (Fi) +

V

+Ψ,⁽s¹⁾(r-r1)(es^'mn(r1)+δsmDn^0'(r1))+

+Ψ,(s2)(r-r1)(hs'mn(r1)+δsmBn0'(r1))]dr1+..., hn(2)(ζ0,r)=[-Ψj,s(r-r1)en'js(r1)+

V ^,                               (8)

+Ψ(s1)(r-r1)λ'sn(r1)]dr1+..., mn2’ (Z0 , F) = J t-^j,s (F - Fl )hnjs (Fl ) +

+Ψ,⁽s²⁾(r-r1)μ^'sn(r1)]dr1+...,

• t^{<2) (Z}0 , ^F)= JI-^ j,s^(F- ^Fl ^)ejs^(Fl ) ^{+ V(l}) ^(F- ^Fl ⁾ⁿs^(Fl ) ⁺

3.    Эффективные свойства композита

+Ψ,(s2)(r-r1)ϑ's(r1)]dr1+..., с учетом равенств (σ0kjui*k ),j =σ0kj,jui*k =0 в силу выполнения уравнений равновесия σ0nj, j =0 для начальных напряжений σ0 (r) в области V и независимости макро*  **

скопических величин umn , En , Hn от координат r. Здесь использована «теорема о свертках», согласно которой дифференцирование ∂ / ∂r(1) i свертываемых функций в подынтегральных выражениях заменено на дифференцирование -∂ / ∂r(1)i или ∂/ ∂ri соответствующих ядер – функций Грина U , Φ, …, Ψ(2) [38] с учетом их разностного аргумента r- r1 и асимптотических равенств нулю при r - rj ^^ . В первом столбце матрицы G функций Грина (5) величины Uik , Φk , Ψk – это перемещения по оси ri , электрический и магнитный потенциалы в точке r от действия в точке r1 единичной силы вдоль координатной оси rk . Во втором и третьем столбцах матрицы G (5) величины Ui(k1) , Φ(k1) , Ψ(k1) и Ui(k2), Φ(k2), Ψ(k2) – это перемещения по оси ri , электрический и магнитный потенциалы в точке r от действия в точке r1 единичного электрического или магнитного источника соответственно. Свойства среды сравнения задаем через тензоры упругих свойств C,, диэлектрической X, и магнитной ц, проницаемостей, пьезоэлектрических е, и пьезомагнитных h, модулей, которые (в различных приближениях) можно приравнять к осред-ненным по объему свойствам C, =< C > , ..., h,=< h> или к свойствам одной из фаз C, = Cf , ., h, = hf или к искомым эффективным свойствам C, = C*, ., h, = h* (схема самосогласования) композита [29; 30; 39]. В (6)–(8) использованы обозначения пульсаций свойств

C '(r) = C(r)-< C >, е '(r) = e(r)-< e > ,

Ц'(r) = Kr)-< ц > , и пульсаций начального напряженного состояния.

o'⁰ (r) = o⁰ (r) - o*⁰, D'⁰ (r) = D⁰ (r) - D*⁰,

B'⁰(r) = B⁰(r) - B*⁰.                   (9)

Тензоры эффективных свойств C^* , λ^* , μ^* , e^*, h^* , в*, n * , д * и дополнительно тензоры электромагнитной κ^*и магнитоэлектрической χ^* связанностей (проявляющиеся в нашем случае лишь на макроуровне) композита с пьезоэлектрическими и пьезомагнитными фазами при наличии начального напряженного состояния ζ₀входят в определяющие соотношения на макроуровне композита

О = С Е ij ijmn mn

-4nijEn -^njH"Р*0,

^Di = eDD) imn^Emn '^ nE ⁺ Xm^Hn '^П0,     (10)

S* = h*B)mn4 +VX + KE + 0*0 , связывая макроскопические значения напряжения o* =< o > , индукций D* =< D >, B* =< B > с деформацией £ =< £ >, напряженностями E =< E >, H* =< H > и температурой нагрева 0 представительной области V композита и в общем случае рассчитываются по формулам [31; 32]

^Cijmn =< ^Cijmn > ⁺< Cijdbadmn,b > ⁺< epijfmn,p > ⁺< hpjjfmn,p > ,

^kn =< ^kn > + < Xkphn,p > + < ekpqbqn,p > ,

^n =< Цkn > + < Wp^n,p > + < hkpqdqn,p > ,

*''(1)'(2) e(a)nij< enij > < Cijpqbqn,p > ⁺< epijhn,p > ⁺< hpijhn,p > ,

*''(1)'(2)

(a)nij        nij             ypq qn,p            py n,p            pj n,p , V 7

*''(1) ^e(D)imn     eimn         eipqapmn,q         'pifm mn,p ,

*''(2) (B) imn       imn            ipq pmn, q          r*ipJ mn, p , xkn =<^kpm®p > + < ekpqdqn, p > ,

^Kkn =pph^p > ⁺< hkpqbqn, p > ,

PU =

j >^-<Cjdbtd,b > ⁺<epjtPp > ⁺<hpjt^p) >,

Л' =<П > ⁺<^-₄,1¹;p) > ⁺< epqtq, p >,

^* =< A > + < *iptS2) > + < ^pqtq,p > , где верхним индексом « ‘ » обозначены пульсации тензоров электромагнитотермоупругих свойств микроструктуры композита. Задача нахождения тензоров C* , …, д * эффективных свойств композита (10) сводится к нахождению полей производных Va(r), Vf(1)(r), ., Vt(2) (r) и последующему осреднению произведений в правых частях равенств (11). Производные коэффициентов Va(r), Vf(1)(r), ., Vt(2)(r) в (11) как результат дифференцирования левых и правых частей уравнений (6)–(8) выражаются через вторые производные функций Грина VVG(r - r1) , где V - оператор дифференцирования по координатам r. В «обобщенном сингулярном приближении» [29] у вторых производных тензорных функций Грина VVG(r - r1) учитываются лишь сингулярные составляющие [38]

VVG(r - r1) ~ G⁵8(r - r1), G^s

s imjn s(1) imn s(2) imn s imn s(1) mn s(2) mn V5 imn V 5 (1) mn V 5 (2) mn для пьезоэлектромагнитной среды сравнения с эллипсоидальным «зерном неоднородности» [29].

Метод периодических составляющих [30; 32; 39]. Рассматриваемые структуры: квазипериодическая (см. рис. 1, c, d), периодическая и статистическая смесь (см. рис. 1, b) имеют одинаковые объемные доли vf , свойства фаз и общие граничные условия вида (3), т.е. p*             p          *             p          *                  s *

upr = ujrj , Ф Г = - Ei ri , V|Г = - Bi ri и up Г = ujrj , ф f =- E* f , у ⁵_Г = - Bi Г . Индексами «p», «5» отмечаем величины этих вспомогательных структур соответственно. Для рассматриваемых двухфазных структур поля пульсаций

С' (r) = Ci1 (r), e' (r) = ei1 (r), h' (r) = hц (r), .,

Сp(r) = Cip'(r), e^p'(r) = ei^p'(r), h^p'(r) = hi,^p'(r), ., (13)

С⁵' (r) = Cif (r), e⁵' (r) = eif (r), h⁵' (r) = hif (r),.

пропорциональны пульсациям соответствующих индикаторных функций i₁ (r), i₁^p (r), i₁^s (r) 1-й фазы (включений), где тензоры разностей C = С, - С₂, e = e₁— e₂, h = h₁-h₂, ...

Производные коэффициентов Va(r), Vf⁽¹⁾(r), ., Vt(²⁾(r) в (11) для двухфазной квазипериодической структуры представим в виде ^                         ^

Va = A + 2Ak (ifk , Vf(1) = Фо + 2Фk(i1)k , ., k=1

^

Vt (2) = T*2) + 2 T(2)(0 k(14)

k=1

и аналогично для периодической структуры

^

Vap = Ap + 2Ak(i1p)k, Vfp(1) = Ф^ + 2Фk(ip)k , k=1

^

., Vtp(2) = Top(2) + 2Tk2)(if)k ,(15)

k=1

где A₀ , Φ₀ , T₀⁽²⁾ , … – некоторые поправки, учитывающие дальний порядок (периодичность, квазипериодичность) структур через формальные составляющие [29] вторых производных функций Грина VVG, для которых < A0 > = < Ф₀> = < Tj²) > = 0. Для статистической смеси имеем ^                               с»

Va5 = 2Ak(if)k , Vf5(1) = 2Фk(if)k , . k=1

s(1)s0

(1)itmn   0 itjs jsmn its smn sm n

(2)s0

its smn sm n , так как a. f(fr-) = U5 C'.   (r) + U(1)5 (e   (r) + 8 D°'(r)) + imn,t   0,           itjs jsmn            its smnsm n

+Ut2⁵ (hmn (r)+8 5_mB„0'(r))+...

или с учетом (13)

amn,.(Zo,r)) = |U ■. C ■   + Uf>⁵(e5„„ +85„Df) +

+ Uff⁵ (h5mn + 8 5mB„⁰)]i1(r) +....

Выполняются равенства

< (Va - Vap)i1 >= p < Va5f >,(18)

< (Vf(1) - Vfpw)i1 >= p < Vf5(1)if >,., < (Vt(2) - Vtp(2))i1 >= p < Vt5(2)if > с учетом доказанного ранее [32] выражения

< i1(if) n-1 > / < if1 >= p,(19)

где n = 2, 3,…, коэффициент корреляции (периодичности) квазипериодической структуры

4i -^v2

p = —11

V1 ^{(1 -}V1)

рассчитывается через v₁₁=< i₁ i₁^p > - относительное объемное содержание в V области пересечения 1-фазы (включений) квазипериодической и периодической структур при их мысленном совмещении, p е (0;1).

Решение «задачи эффективного модуля» – поиск тензоров С*, X*, ц, e*, h*, к*, х*, в*, п*, Д’ пьезокомпозита (10), (11) с разупорядоченной (квазиперио-дической) двухфазной структурой рассмотрим на примере нахождения решения для его тензора С^* эффективных упругих свойств. Для этого запишем общие формулы для расчета тензоров эффективных упругих свойств рассматриваемых (квазипериодической, периодической, статистической смеси) структур двухфазных пьезокомпозитов

^

Vt⁵(²⁾= 2Tk²⁾(if)^k , k=1

С* =< С > + < 11л >,

так как для нее дальний порядок отсутствует, а ближний – форма включений – учитывается формой «зерна неоднородности» сингулярной составляющей (14). В (14)–(16) компоненты тензоров Ak , Φk , …, Tk(2) зависят от начального напряженного состояния ζ0 и выра- жаются через сингулярные составляющие G s (14) вторых производных функций Грина VVG, например, компоненты тензора A1 имеют вид

А- ijmn

(1)               (2)

ijdb dmn,b      pij mn,p      pij mn,p

С^p* =< С > + < i_x^p'X^p >,

A^p = C,_ha^p  +e e-f^p(1)+ h-f^p (²⁾;

ijmn ijdb dmn,b pij mn,p pij mn,p с 5 * =< с > + < i5x5 >,

A 5 ijmn

= C-a_ha^Sa  „+ e f⁵⁽¹⁾+ h  Г(²⁾

ijdb dmn,b pij mn,p      pij mn,p с учетом (6)–(8), (11) или в виде

^           — —

С - < С >=< (i1)²> Л = V1 (1 - v₁)Л , Л =< Л >1 - < Л >2;

С^p* - < С >=< (i1^p')² > Л^p = v1(1 - v1 )Л^p,

Л p< Л ^p> p 1 -< Л ^p> p 2;

С¹ *-< С >=< (if)²> Лs = v1 (1 -v₁)Лs,

Л s =< Л s > s 1 -< Л s > s 2, где < ... >12 — операторы осреднения по 1-й или 2-й фазам соответствующей структуры, имеем пропорциональные зависимости (13) вида

Л = Лi, Л^p = Лi1^p', Лs = Лi^'          (23)

с учетом (22), < Л > = < Лp > = < As > = 0. При этом для статистической смеси имеем то

С s * =< С > + < if Л^s >=< С > +У Л,,. < (is') k⁺¹>

1(k)1

к =1

или то

^С=< ^С> ⁺^ ^Л(k)m(к+1) к=1

с учетом разложения то

Л s = £ Л( к)(4^s)^к                 (25)

к=1

и обозначения компонент

(к )jmn (Zo) = CijdbA(к) dbmn (Zo)

• (1)                          (2)

epij   (k) pmn^(ζ0⁾     pij   (k) pmn^(ζ0^),

тензора Λ_(k), центрального момента k-го порядка

m(к) =< (О^к >= V1(1 - V, )[(1 - v,)^к-1- (-vj^к-1], (27)

риодической и периодической структур в (28) вычтем из первого уравнения второе, получив отклонения то

Л . Л - Л^р = £ Л(к)[(i1)^к - (if)^к ].       (29)

к=1

После умножения левой и правой частей (29) на пульсацию i1 (r) и последующего осреднения получим выражение то                                                                       то

• < <л >= £ Л(к) < (i1)^к+1- ifi1p)^к > = (1 - р)£Л(к)m(к+1)

к=1                                                       к=1

с учетом < (if^к+1>-<ifif)^к >= (1 -р)m(к+_п(19), (27) или в окончательном виде

• <    i Л° >= (1 - p)(Сs* - < С >)          (30)

то с учетом Сs* =< С > +^ Л(к)m(к+1) (24). Левую часть (30) к=1

< ^Л” > запишем в ином виде < ^Л” >=< i_YЛ > - < i_YЛ^p > или

• <    i1 Л° >= С* -< С >+ p(С^p* -< С >),     (31)

так как имеем

• <    i_xЛ >=< i₁i₁> Л = v1(1 - v₁)A = С* - < С > ,

• <    11Л^p >=< iff' > Л^p = p< ip ip > Л^p =

= pv1(1 - v₁)A^p = p(С^p* - < С >)

с учетом (19)–(23), (25). Приравнивая правые части выражений (30) и (31), получим искомое решение

С* = p С^p * + (1 - p )С s *.              (32)

Таким образом, для пьезокомпозита с квазиперио-дической двухфазной структурой (по аналогии с решением (32) для С* ) имеем решение где v1 =< i1 > - относительное объемное содержание 1-й фазы композита. Аналогичные (25), (26) разложения для квазипериодической и периодической структур имеют вид (21)

C

K

X*

С* =< С > + < /. Л >,

С^p* =< С > + < i1^pЛ^p >,

то

Л = Ло + £ Л к (i1)^к, к=1

то

Л^p = ЛР + £ Л( к)(i1p)^к, к=1

здесь Λ0 , Λ0p – поправки, учитывающие наличие «ближнего» (локальную упорядоченность, форму и размер включений, непрерывность матрицы) и «дальнего» порядка (периодичность, квазипериодичность) структур через «формальные составляющие» [29] вторых производных функций Грина WG. С учетом предполагаемого равенства поправок Лp ~ Ло квазипе- для тензоров эффективных упругих свойств C* , диэлектрической λ* и магнитной μ* проницаемостей, пьезомеханических свойств e* и h* , коэффициентов электромагнитной κ и магнитоэлектрической χ связанностей, температурных напряжений β* , векторов *

эффективных пироэлектрических π и пиромагнитных О* постоянных, которые выражаются (33) через решения Cs*,^, Оs* обобщенного сингулярного приближения (12) [29] для «статистической смеси» и решения

Cp*, .., 0p* [20-23, 26, 27] для периодической структуры. Отметим, что для статистической смеси коэффициент периодичности p = 0.

В обобщенном сингулярном приближении тензоры C1 *,., ^* (33) эффективных свойств двухфазного композита с начальным напряженным состоянием рассчитываем через тензоры A , B ,…, T(2) , которые входят в разложения uti = jum n + BjE + DyH + T 0,

• (1)    * (1) * (1) * (1) i imn mn in n in n i^,

• (2)    * (2) * (2) * (2) i imn mn in n in n i

с учетом представления пульсаций производных перемещений u_i^'_{, j}(r), напряженностей электрического и магнитногоH(r) полей в виде

'*'

Uj (r) = u, j (r)^-Uj = ^u_v ii(r), E (r) _ E(r)-E = E ii(r), H (r) = H(r) - H = H Z1(r).

Тензоры A , B ,…, T(2) находим из решения соот- ветствующих четырех независимых систем линейных алгебраических уравнений общего вида [A] {X} = {B} с матрицей коэффициентов [38]

[A] =

(1,2) ^aijd

(2,2) ^a

(3,2) ^a

(1,3

(2, ik

(3,3) ^a

когда для   ^1-Й   системы   {X} = ^{Aksmn , F^, , Fk^²*},

(1)     (2) (3)                                                          (1)(2)

ijmn^,imn^,imn^,                                       ksn^,dn^,dn^,

(1) (2) (3)                                                                      (1)(2)

{c_ijn ,c_in ,c_in }, для 3-й системы   {D_ksn ,M_dn ,M_dn },

(1)     (2)     (3)                                                                      (1)(2)

{d_ijn ,d_in ,d_in }, для 4-й системы {T_ks ,T_d ,T_d }, { f_ij⁽¹⁾ , f_i⁽²⁾ , f_i⁽³⁾ } соответственно. Начальное напряженное состояние учитывается видом коэффициентов

а(1’1) =5-^ - -U* JС^+З^+а-ЗкХС^ +8„о°)]- ijks tk js     tjdb ^ dbks   d^dk^bs V 1/V dbks     dkb bs 7]

• -    Usк [e^dh + 8_dtD_s^:0 + (1 - 2V,)(e_dk + 8Д°)] -ij            s               s                    1 s               s

• -    ¹²⁾Гh + 8,A'° + (1 - 2v )(h_db + 8J" )], ijd dks dk s                1 dks dk s

a.⁴⁾ =-ФSdb [Cdbks +8dk^bs + (1 -2V1)(Cdbks + 8dkabs)]- (35)

• -    Фsj¹)^[ed_k + 8^*,D⁰ + (1 - 2v)(e_dk + 8_tD¹)^] -id dks dk s                1 dks dk s

• -    Ф^) [hidk, + 8,A'° + (1 - 2V)(h_dk + 8J0)] , id dks dk s                1 dks dk s

• a. = "* sdb [ Cdbks + 8 dk a ° + (1 - 2 V1)( Cdbks + 8 dk a)] -

• -V ^ [ edks + 8 D + (1 - 2 V1)( e + 8 dkDs)] -
• -V ^) [ hidb + 8,Д'° + (1 - 2 V)(hdk + 8J°)] is   s        ss

первого столбца матрицы [A] и видом компонент

b(1) = ULCt + Us^Ce +8^D°) + Us(2)(h + 8t B°), ijmn ijks ksmn ijk kmn km n ijk kmn km n , (2)        s                  s(1)                     0         s(2)0

imn       iks  ksmn ik    kmn km n        ik     kmn km n^,

• (3)    s                   s(1)                      0          s(2)0

• ^uimn ^T iksCksmn^{+ T} ik⁽ekmn^{+ u}km^Dn ) ^{+ T} ik V*ктп^{+ u}kmBn )

вектор-столбца {B} с учетом сингулярных составляющих Gs (12). Здесь использованы обозначения тензоров разностей C , e , … (13) и дополнительно тензоров C =< C > -C., ., Д =< p > -p. - отклонений осреднен-ных значений тензоров < C > , ., < p > композита от соответствующих тензоров C., ., р. среды сравнения. Использовано представление полей начального напряженного состояния в виде о° (r) = о*° + 6°i1 (r), D° (r) = D*° + D°i1 (r),

B°(r) = B*° + B°i1(r)                 (37)

с учетом выражения пульсаций

6'° (r) = 6°i'1 (r), D'° (r) = D°i'1 (r), B'° (r) = B°i1 (r) через пульсацию i₁^' (r) индикаторной функции i₁ (r) для 1-й фазы, где тензоры разностей

000 000000

6 = 61 - 62 , D = D1 - D2 , B = B1 - B2 •   (38)

Отметим, что ранее в [39] сделан вывод, что в решении (33) «статистическая смесь» – это полидис-персная структура (см. рис. 1, b) в виде двух взаимопроникающих кластеров частиц каждой из фаз. Этот вывод сделан на основе анализа аппроксимаций (разложений) двухточечных корреляционных функций в трансверсальной плоскости однонаправленных волокнистых (матричных) квазипериодических структур (см. рис. 1, c, d) по «базовым» корреляционным функциям периодической (гексагональной) структуры и статистической смеси (см. рис. 1, b). Тензоры эффективных свойств C^s*,., d^s* такой полидис-персной кластерной структуры (статистической смеси) могут быть определены по схеме самосогласова-ния из решения известной задачи для одиночного включения (волокна) в «эффективной среде» [28] или по формулам обобщенного сингулярного приближения [38] (34)-(36), когда тензоры C", X", р", e", h"

среды сравнения приравнены к соответствующим искомым тензорам C^s* , λ^s* , μ^s* , e^s* , h^s* статистической смеси с учетом начального напряженного состояния ζ₀ (37), (38). Вычисление тензоров эффективных свойств пьезокомпозита с периодической структурой C^p* ,…, ϑ^p* в формулах (33) в общем сводится к решению задачи электромагнитотермоуп-ругости на ячейке периодичности и представляет собой отдельную сложную задачу [20–23, 26, 27]. Во многих работах, например [29–32], отмечается, что значения эффективных упругих свойств многих матричных композитов с периодическими структурами близки к решению для полидисперсной матричной структуры (см. рис. 1, а) и к решению обобщенного сингулярного приближения при приравнивании свойств среды сравнения к свойствам матрицы композита. Поэтому тензоры C^p* ,…, ϑ^p* в (33) также могут быть рассчитаны по формулам обобщенного сингулярного приближения [38] (34)–(36) при приравнивании тензоров C^•, λ^•, μ^•, e^•, h^•среды сравнения к соответствующим тензорам C₂ , λ₂ , μ₂ , e₂ , h₂ матрицы (например, 2-й фазы) композита. В [34] для продольного коэффициента электромагнитной связанности κ^*₃₃ однонаправленных волокнистых композитов с пьезоэлектрическими и магнитострикционными фазами (матрицей и/или волокнами) установлена тождественность аналитических решений по различным расчетным схемам: «волокно/матрица» в виде составной цилиндрической ячейки или «волок-но/матрица/эффективная среда» с размещением такой ячейки в эффективной среде (схема самосогласова-ния) (см. рис. 1, а) [28], обобщенного сингулярного приближения [38] при приравнивании свойств среды сравнения к свойствам матрицы композита. При этом для композита «феррит/пьезоэлектрик» (пьезоэлектрические волокна в ферритовой матрице) установлено совпадение этого решения κ^*₃₃ с решением асимптотического метода осреднения [21] для κ^*₃₃ идеальной периодической волокнистой структуры.

В отсутствие начального напряженного состояния для трансверсально-изотропного (с осью симметрии r₃ ) композита тензоры эффективных пьезоэлектрических e^* и пьезомагнитных (магнитострикционных) h^* модулей, электромагнитной κ^* и магнитоэлектрической χ^* связанностей (10), (11) в матричной форме записи имеют вид [19–25; 31; 32]

eij  =

* e₃₁

0    0    0   e₁^*₅ 0

0   0  e1*500

e3*1 e3*3

hij

0 _h3*₁

0    h1*4 h1*5

0    h1*5   -h1*4

h3*3

κij =

* κ11	* κ12	0
* -κ12	* κ11	0
0	0	* κ33

,  χ*ij  =  κ*ij   , где верхним индексом «T» обозначена операция транспонирования, тензорные и матричные индексы связаны между собой соотношениями: 11 → 1 , 22 → 2 , 33 → 3 , 23 и 32 → 4, 13 и 31 → 5 , 12 и 21 → 6 . Для случая заданных на макроуровне композита значений начальных деформаций ε*0 , напряженностей элек- трического E*0 и магнитного H*0 полей соответствующие значения для фаз ζ0f ≡< ζ0>f= {σ0f,D0f,B0f}, в частности, тензоры σ10,2 , D10,2 , B10,2 двухфазного композита (12), могут быть найдены, например, по известному решению [38] без начального напряженного состояния, где <... >f=1/ Vf ∫Vf ... dr – оператор осреднения по области Vf f-й фазы композита, V = ^ 2=1 Vf .

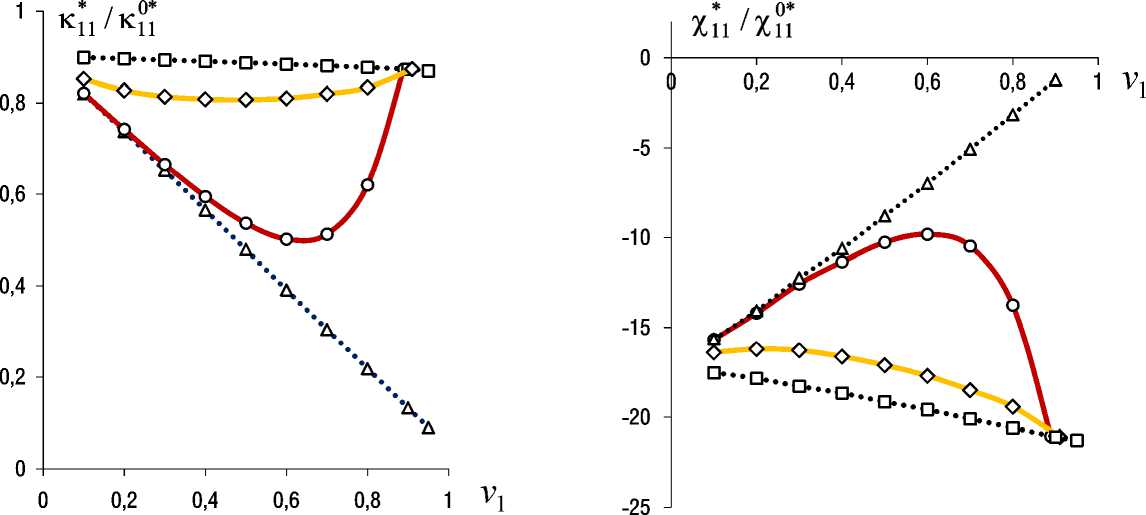
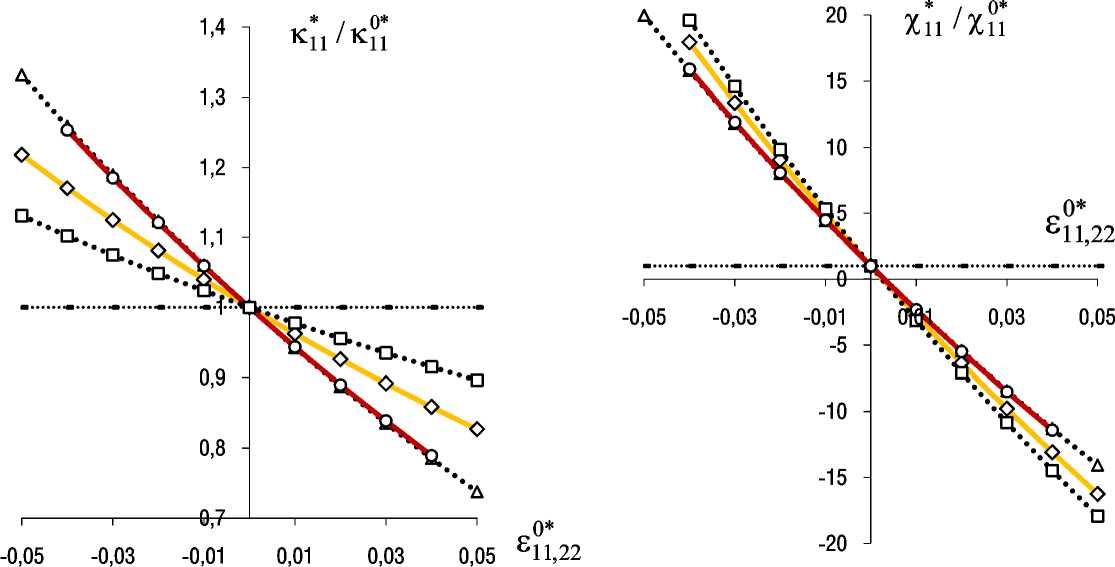
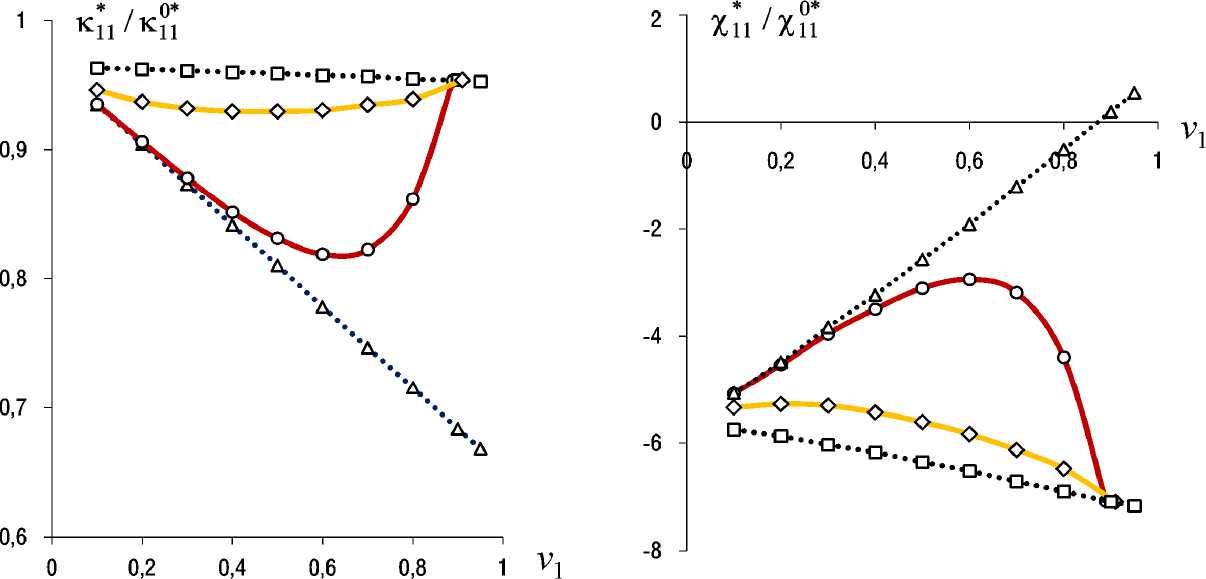
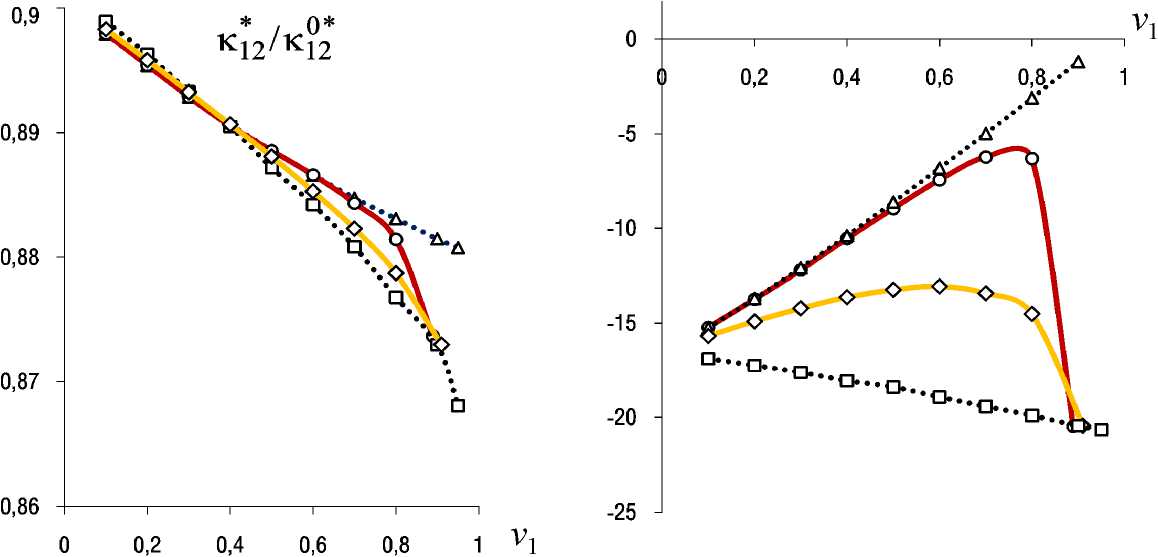
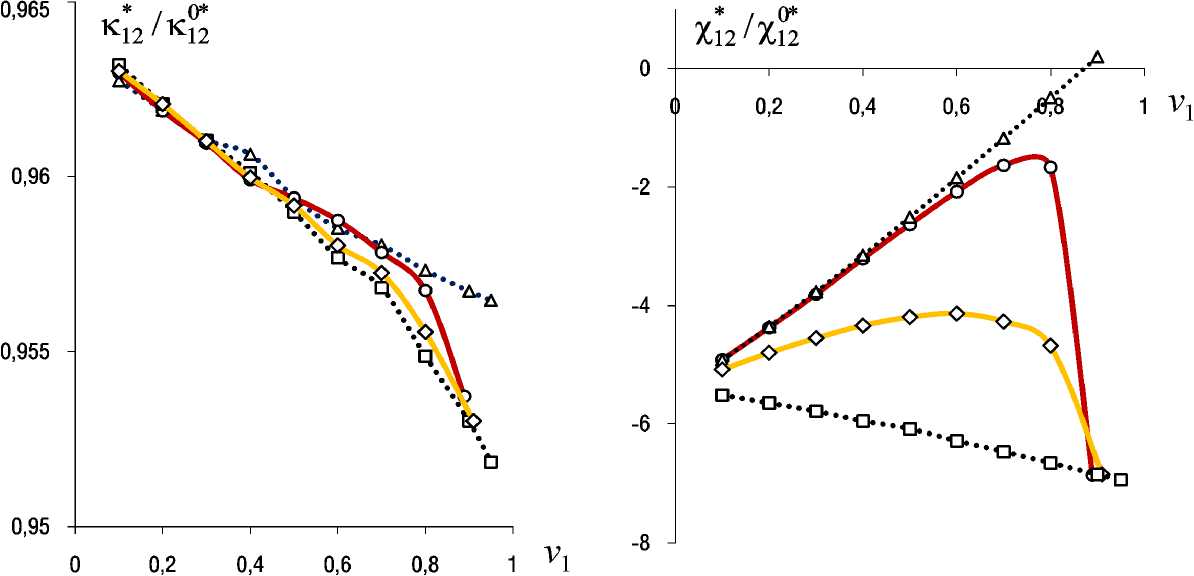
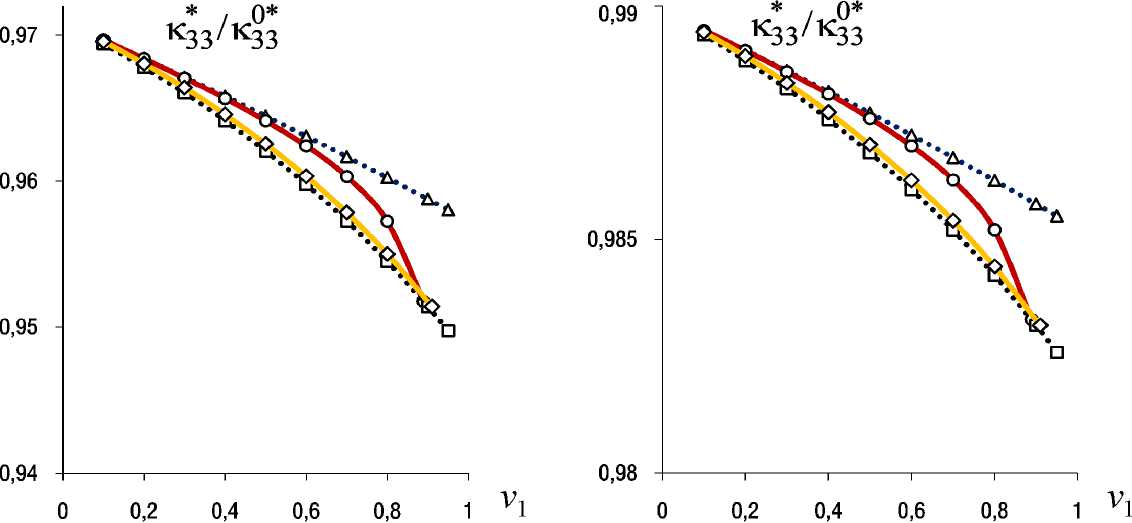
4. Результаты численного моделирования

Результаты вычисления относительных значений независимых эффективных коэффициентов электромаг*^*

нитной ( κ ) и магнитоэлектрической ( χ ) связанностей трансверсально-изотропного композита «PZT-4/феррит» с различными (квазипериодическими и вспомогательными) структурами (см. рис. 1) представлены в виде графиков на рис. 2–7 в зависимости от значений объемной доли v1 ферритовых волокон, компонент ( ε₁⁰₁^*= ε⁰₂^*₂≠0 и/или ε⁰₃^*₃≠0 ) осесимметричного тензора

0*

начальной макродеформации ε при E⁰= 0, H⁰= 0 .

Выполняются равенства κ₁^*₁= κ^*₂₂ , χ₁^*₁= χ^*₂₂ , κ₁^*₂= -κ^*₂₁ , χ₁^*₂= -χ^*₂₁ , κ^*33 = χ^*33, при этом имеем κ₁^*₂ / κ₁⁰₂^* =

κ^*₂₁ / κ⁰₂^*₁ , χ₁^*₂ / χ₁⁰₂^* = χ^*₂₁ /χ⁰₂^*₁. На рис. 2–7 использованы обозначения (◊, ○) графиков решений для квазиперио-дических структур: «со смещением» волокон (◊) (см. рис. 1, c) при степени разупорядоченности k = 1 и «с удалением» волокон (○) (см. рис. 1, d) в гексагональных ячейках. Решения для периодической структуры (□) и статистической смеси (Δ) получены по формулам обобщенного сингулярного приближения [38] при приравнивании свойств среды сравнения к свойствам матрицы (PZT-4) композита или к осред-ненным по объему композита значениям соответственно. Выявлены линейные зависимости, например на рис. 3, относительных значений всех ненулевых

Рис. 2. Эффективные коэффициенты κ₁^*₁(а), χ₁^*₁(b) композита «PZT-4/феррит» в зависимости от объемной доли v₁ волокон для случая ε₁⁰₁^*= ε⁰₂^*₂= 0,05, ε₃⁰₃^*=0

Fig. 2. Effective coefficients κ₁^*₁(а), χ₁^*₁(b) of the composite "PZT-4/ferrite" depending on the volume fraction v₁ of fibers for case ε₁⁰₁^*= ε⁰₂^*₂= 0.05, ε₃⁰₃^*=0

а                                                     b

Рис. 3. Эффективные коэффициенты κ₁^*₁(а), χ₁^*₁(b) композита в зависимости от начальной макродеформации ε₁⁰₁^*_,22, ε⁰₃₃^*=0 для случая v₁ = 0,2

Fig. 3. Effective coefficients κ₁^*₁(а), χ₁^*₁(b) of the composite depending on the initial macrostrain ε₁⁰₁^*_,22, ε₃⁰₃^*=0 , for case v₁ = 0.2

компонент тензоров κ^* , χ^* от значений ε₁⁰₁^*_,22, ε⁰₃₃^* осесимметричного тензора начальной макродеформации ε^0*композита. На рис. 3 графики решений без учета начального напряженного состояния обозначены символом (▬). При предельной объемной доле волокон v_1max ≈ 0,9 обе квазипериодические структуры (см. рис. 1, c, d) вырождаются в одну периодическую структуру, поэтому на рис. 2, 4–7 решения (◊, ○) для квазипериодических структур при v_1max совпадают с решением (□) для периодической структуры.

Заключение

Разработана математическая модель начально-напряженного (на микро- и макроуровнях) композита c пьезоэлектрическими магнитострикционными фазами, с использованием которой получено численно-аналитическое решение задачи «эффективного модуля» начально-напряженного квазипериодического композита в рамках обобщенного сингулярного приближения статистической механики композитов. Представлены результаты расчета всех независимых компонент тензоров

Рис. 4. Эффективные коэффициенты κ₁^*₁(а), χ₁^*₁(b) композита в зависимости от объемной доли v₁ волокон для случая ε₃⁰₃^*=0 0,05, ε₁⁰₁^*_,22=0

Fig. 4. Effective coefficients κ₁^*₁(а), χ₁^*₁(b) of the composite depending on the volume fraction v₁ of fibers for case ε₃⁰₃^*=0 0.05, ε₁⁰₁^*_,22=0

а                                                     b

Рис. 5. Эффективные коэффициенты κ₁^*₂(а), χ₁^*₂(b) композита в зависимости от объемной доли v₁ волокон для случая ε₁⁰₁^*= ε⁰₂^*₂= 0,05, ε₃^0*₃=0

Fig. 5. Effective coefficients κ₁^*₂(а), χ₁^*₂(b) of the composite depending on the volume fraction v₁ of fibers for case ε₁⁰₁^*=ε⁰₂^*₂= 0.05, ε₃⁰₃^*=0

эффективных коэффициентов электромагнитной κ^* и магнитоэлектрической χ^* связанностей трансверсальноизотропного однонаправленно-волокнистого композита «PZT-4/феррит» при осесимметричном тензоре начальной макродеформации ε^0* композита, когда компоненты ε₁⁰₁^*= ε⁰₂^*₂≠ 0 и / или ε₃⁰₃^*≠0. Выявлено, что при осесимметричном тензоре начальной макродеформации ε^0* композита тензоры κ^*, χ^* по-прежнему имеют однотипный вид (39), но не связаны транспонированием

χ^*≠ κ^*T, χ^*₃₃= κ^*₃₃для рассмотренных случаев: ε₁⁰₁^*= ε⁰₂^*₂≠0 и/или ε₃⁰₃^*≠0 осесимметричного по оси r3 начального напряженно-деформированного состояния композита. Для всех ненулевых значений компонент тензоров κ^*, χ^* выявлены, во-первых, монотонность (как убывающих, так и возрастающих) зависимостей относительных величин κ^*/κ^0*, χ^*/χ^0* от объемной доли ферритовых волокон v1 (см. рис. 2, 4–7) для базовых структур: периодической структуры (□) и статистической смеси (Δ),

Рис. 6. Эффективные коэффициенты κ₁^*₂(а), χ₁^*₂(b) композита в зависимости от объемной доли v₁ волокон для случая ε₃⁰₃^*= 0,05, ε₁⁰₁^*_,22=0

Fig. 6. Effective coefficients κ₁^*₂(а), χ₁^*₂(b) of the composite depending on the volume fraction v1 of fibers for case ε₃⁰₃^*= 0.05, ε₁⁰₁^*_,22=0

Рис. 7. Эффективный коэффициент κ^*₃₃композита в зависимости от объемной доли v₁ волокон для случев: ε1⁰1^*= ε⁰2^*2= 0,05, ε3⁰3^*=0 (а), ε⁰33^*= 0,05, ε1⁰1^*,22=0 (b)

Fig. 7. Effective coefficient κ^*₃₃of the composite depending on volume fraction v₁ of fibres for cases: ε1⁰1^*= ε⁰2^*2= 0.05, ε3⁰3^*=0 (а), ε⁰33^*= 0.05, ε1⁰1^*,22=0 (b)

и существенная немонотонность этих зависимостей для квазипериодических структур (◊, ○) (см. рис. 1, c, d). Во-вторых, выявлены линейность и монотонно убывающий характер зависимостей относительных величин κ*/κ0*, χ*/χ0* от значений начальных осевых макродеформаций ε101*,22 и/или ε033* композита (например, на рис. 3) с учетом равенств κ/κ0= χ/χ0= 1 при ε0* = 0 . Различия прямолинейных графиков (см. рис. 3) величин κ*/κ0*, χ*/χ0* состоят в различиях значений коэффициента пропорциональности, т.е. в угле наклона графиков к оси абсцисс – начальной осевой деформации: ε101* , ε02*2 , ε303* при фиксированном значении объемной доли волокон v1. Пропорции в различиях угла наклона графиков этих величин κ*/κ0*, χ*/χ0* (например, на рис. 3 при v1 = 0,2) обусловливаются пропорциями этих величин на графиках концентрационных (существенно немонотонных для квазипериодических структур) зависимостей на рис. 2, 4–7 при соответствующем значении v1 (например, на рис. 2 при v1 = 0,2). Таким образом, увеличение абсолютных значений компонент тензоров κ*, χ* рассматриваемых структур композитов

(см. рис. 1) имеем при отрицательных значениях компонент ε101* , ε 022* , ε033* осесимметричного тензора начальной макродеформации ε0* композита. Наиболее существенное влияние имеем для компонент χ1*1 (см. рис. 2, b, рис. 3, b), χ1*2 (см. рис. 5, b) для случая ненулевых значений начальных осевых макродеформаций ε101*,22 в трансверсальной плоскости композита. В случае комбиниро- ванного начального макродеформирования композита, когда одновременно имеем ε101*,22 ≠0 , ε30*3 ≠0, тогда результирующие значения относительных величин κ*/κ0*, χ*/χ0* находим суммированием соответствующих «коэффициентов влияния» κ*/κ0*, χ*/χ0* от каждой из компонент ( ε101*,22 , ε303* ) осесимметричного тензора начальной макродеформации ε0* композита.