Электромагнитная волна в заряженном конденсаторе

В [1] рассматривается электромагнитное поле конденсатора в цепи переменного тока. Здесь рассматривается электромагнитное поле в заряжаемом конденсаторе и то поле, которое продолжает существовать в заряженном конденсаторе.

Здесь также рассматриваются уравнения Максвелла в системе СГС следующего вида с отличными от единицы величинами ε , µ :

rot(E)+ ^ ^H = 0,(1)

c dt rot(H)- - ®E = 0 ,(2)

c о t div(E )= 0,(3)

div ( H ) = о ,

где

• H, E - ток, магнитная и электрическая напряженности соответственно,

• s, ц - диэлектрическая проницаемость, магнитная проницаемость.

2.    Решение системы уравнений

Как и в [1] рассмотрим решение системы уравнений Максвелла (1.1-1.4). В системе цилиндрических координат r, ф , z эти

уравнения имеют вид: Er дE, 1 — + —- + -• r дr r 8E^ +aEz- = 0, дф   дz (1) 1 .aE. -ж, = r дф   дz dH v^T, dt (2) дEr  дE —r---z- = v дz    д r dHϕ dt ’ (3) E dE 1 ϕϕ 1 r д r r дEr    dHz --r- = v z-, дф     dt (4) Hr  дHr  1 —- + —- + -• r    д r r H + ^ = 0, дф   дz (5) 1 дHz  дНф • r  дф дz dE = q— dt (6) дHr  дHz = ( дz    д r dEϕ q^T (7) Нф + дНф  1 + r д r r дHr   dE ---- = q—-дф     dt (8) где v = -Ц c, (9) q = S c, (10) • электрические напряженности Er, EФ, Ez: • магнитные напряженности Hr, Нф , Hz - Для сокращения записи в дальнейшем следующие обозначения: co = со^(аф + xz), будем применять (11) si = sin(aф + xz),

где a, x — некоторые константы. Представим неизвестные функции в следующем виде:

Hr. = hr (r )co • (exp(tot) -1),(13)

H^- = 4(r) si • (expto)- 0,

H. = hz (r) si • (exp(at) -1),(15)

Er. = er (r )si • (1 - exp( tot)),(16)

Еф- = еф(r)co •(1 - exp(tot)),(17)

Ez. = ez (r)co • (1 - exp(rot)),(18)

При этом ток смещения

Jz = —Ez = -to • ez (r) co • exp(rot)

dt

На рис. 1 показаны эти переменные, как функции времени, и их производные по времени при to = - 300 : H z - сплошные линии, E z - пунктирные линии, J_z - точечная линия. Можно убедиться, что в системе уравнений (1-8) амплитуды всех напряженностей при t ^ та одновременно стремятся к постоянному значению, а амплитуда тока стремится к нулю. Это соответствует заряду конденсатора через постоянное сопротивление.

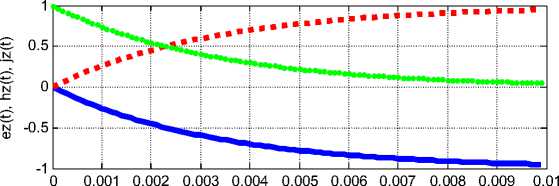
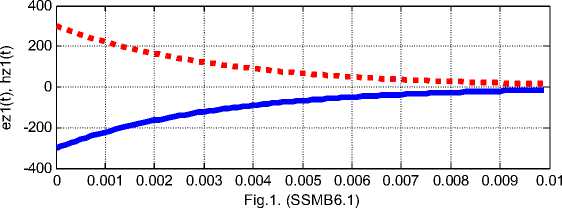
После заряда конденсатора ток прекращается. Однако, как показывается ниже, стационарный поток электромагнитной энергии сохраняется.

Непосредственной подстановкой можно убедиться, что функции (13- 18 ) преобразуют систему уравнений (1-8) с четырьмя аргументами r , ф, z , t в систему уравнений с одним аргументом r и неизвестными функциями h ( r ), e ( r ) . Эта система уравнений имеет вид:

r () + е ф ( г )    ф а X" ez ( r ) = 0 , rr	(21)
1                Н^ ---e z ( r ) а + е ф ( r ) X--h r = 0 rc	(22)
e r ( r ) X - e z ( r ) + — А ф = 0 c	(23)
е ф ( r ) , , ( x er ( r )     , M® A + е ф ( r )         "  а +      h z = 0, r   rc	(24)
r ( ) + h r ( r ) + ф    а + X" h z ( r ) = 0 , rr	(25)
1 "  h z ( r ) а - h v ( r ) X - — e r = 0 , rc	(26)
- h r ( r ) X - h z ( r ) +— е ф = 0 c	(27)
А ф ( r )           h ( r )      £® —--+ h ф ( r ) + rV ' • а +-- ez ( r ) = 0 . r ϕ rc	(28)

Она полностью совпадает с аналогичной системой уравнений для конденсатора в цепи переменного тока [1]. Решение этой системы также полностью совпадает с полученным в [1] и имеет

следующий вид: еф(r) = kh(а, x, r) (30) er (r )=а (еф(r)+r • e’(r)), (31) ez(r)=r • еф(r) - ’ α (32) аф (r)=- ^^er (r), cχ (33) hr (r )= ^^еф (r)1 , cχ (34) hz (r) = 0.

где kh() - функция, определенная в [1],

q =

х -

V

цею¹ c 2 X

Таким образом, решение уравнений

Максвелла для

заряжаемого

конденсатора и для конденсатора в

цепи

синусоидального тока отличаются только тем, что в первом случае присутствуют экспоненциальные функции времени, а во втором - синусоидальные.

3.    Напряженности и потоки энергии

Также, как и в [1], плотности потоков энергии по координатам определяются по формуле

5 =

S r

S ϕ

S z

= п Ц r ,Ф

s_r • sii

s ^ • si • co

s_z • si • co

dr • dф .

где

s r = ( е_Ф^ ^{- e}z h _v ) s ^ = ( e z h r ^- e r h z X s z = ( еЛ ф ^- e ₉ h r ) П = c / 4 n .

0    0.05   0.1

0    0.05   0.1

-1

0    0.05   0.1

Fig.1. (SSB6(3).m)

-5000

0    0.05   0.1

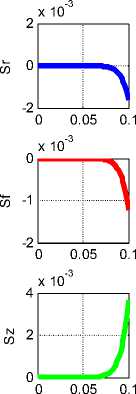
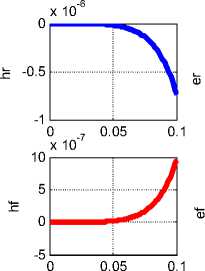
Рассмотрим функции (2) и e r ( r ), e ^ ( r ), e z ( r ) , h r ( r ), h ^ ( r ), h z ( r ) . На рис. 1 показаны, например, графики этих функций при A = 1, а = 5.5, Ц = 1, 8 = 2, X = 50, ® = 300 . Условия этого примера отличаются от условий аналогичного примера в [1] для конденсатора в цепи переменного тока только значением параметра to = - 300 (в [1] to = 300 ). Видно, что эти функции отличаются только знаками.

Еще раз надо подчеркнуть, что эти функции не равны нулю в любой момент времени, т.е. после заряда конденсатора ток смещения прекращается, электрические и магнитные напряженности остаются, принимая стационарное, но отличное от нуля значение.

Остается также стационарный поток электромагнитной энергии. Существование стационарного потока не противоречит существующим физическим представлениям [2]. Существование такого потока в статической системе рассматривает Фейнман в [3]. Он приводит пример потока энергии в системе, содержащей только электрический заряд и постоянный магнит, покоящиеся рядом.

Существуют и другие эксперименты, демонстрирующие тот же эффект [4]. На рис. 2 показан электромагнит, сохраняющий силу притяжения после отключения тока. Предполагают, что такими электромагнитами пользовался Эд Леедскалнин при строительстве знаменитого Кораллового замка – см. рис. 3 [4]. В таких конструкциях в момент отключения ток электромагнитная энергия имеет некоторое значение. Эта энергия может рассеяться путем излучения и тепловых потерь. Однако, если эти факторы не существенны (по крайней мере, в начальный период) электромагнитная энергия должна сохраняться. При наличии электромагнитных колебаний должен возникнуть и распространяться поток электромагнитной энергии ВНУТРИ конструкции. Прерывание этого потока может быть достигнуто разрушением конструкции. При этом в силу закона сохранения энергии должна быть совершена работа, эквивалентная той электромагнитной энергии, которая исчезает при разрушении конструкции. Это означает, что "разрушителю" нужно преодолеть некоторую силу. Именно это и демонстрируется в указанных экспериментах. Очень хороший эксперимент показан в [11]. В [5] рассматриваются математические модели таких конструкций, построенные на основе уравнений Максвелла. Выявляются условия, при соблюдении которых поток электромагнитной энергии сохраняется сколь угодно долго.

Рис. 2.                           Рис. 3.

Итак, в конденсаторе формируется стационарный поток электромагнитной энергии. Рассмотрим подробнее структуру этого потока. Из (2.11, 2.12, 3.1) следует, что в каждой точке диэлектрика

проекции потоков энергии определяются по формуле: Sr sr • si2         sr • sin2(ap+xz) S = S, = sp • si • co = s, • °-5sm(2(aP + xz)) .          (4) _Sz _    sz • si • co     sz • 0.5sin(2(ap + xz)) где, как следует из (2.30-2.35, 3.2),

sr = (- ezhp )

q εω αχc

r • e p ⁽ r ) • e r ^{( r} )

s p =⁽ e z h r ^{) =} q — r • eU.r ) αχc

s z = ⁽ e r h p - e p h r ) = - ^ ( e ^{2 ( r )+} e P ⁽ r ) ) χc

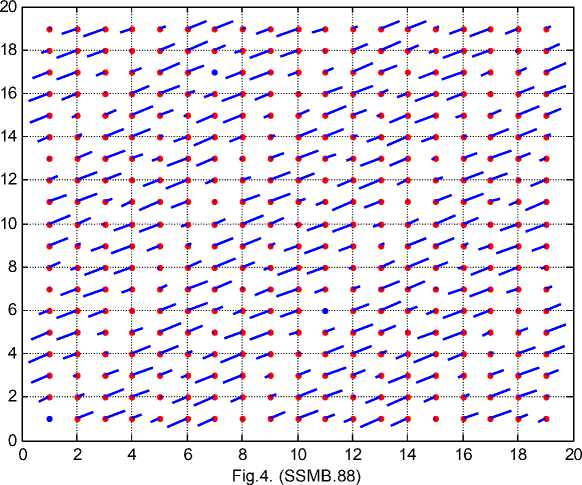
Рассмотрим, например, развертку цилиндра с данным радиусом r . На окружности этого радиуса вектор Sr направлен всегда в сторону увеличения радиуса и колеблется по величине, как sin2 (ap + xz) • Суммарный вектор (Sp + Sz) наклонен к линии радиуса всегда под углом arctg(s zJsp), а величина этого вектора

колеблется как sin ( 2( ap + xz ) ) • На рис- 4 показано векторное поле

( р + S z ) при a = 1.35, X = 50 • Здесь горизонталь и вертикаль соответствуют координатам ϕ , z

4.    Обсуждение

Показано, что в заряжаемом конденсаторе распространяется электромагнитная волна, а математическое описание этой волны является решение уравнений Максвелла. При этом в теле диэлектрика (т.е. там, где существует напряженность e_z ) существуют электрические и магнитные напряженности . Существуют также

• •    круговой поток энергии S_p, меняющий знак,

• •    вертикальный поток энергии S_z, меняющий знак.

• •    радиальный поток энергии Sr, всегда направленный от центра; это означает, что заряженный конденсатор излучает через боковую поверхность.

5.    Конденсатор с магнитом

Поток энергии продолжает существовать и в заряженном конденсаторе как стационарный поток электромагнитной энергии. Именно в этом потоке циркулирует электромагнитная энергия, запасенная в конденсаторе. Следовательно, та энергия, которая содержится в конденсаторе и которую принято считать электрической потенциальной энергией, является электромагнитной энергией, хранящейся в конденсаторе в виде стационарного потока . 144

Известны эксперименты по обнаружению магнитного поля между обкладками заряженного конденсатора с помощью компаса [6, 7]. В соответствии с изложенным в круглом конденсаторе должно наблюдаться только расположение стрелки компаса перпендикулярно радиусу круглого конденсатора. Наблюдаемое отконение стрелки от оси конденсатора можно объяснить неравномерностью распределения заряда по квадратной пластине.

Выше был рассмотрен заряженный конденсатор, между обкладками которого существует электрическая напряженность . Рассмотрим теперь не заряженный конденсатор, между обкладками которого расположен постоянный магнит. Это означает, что между обкладками конденсатора существует магнитная напряженность . В силу симметрии уравнений Максвелла в "зазоре" такого конденсатора должно существовать электромагнитное поле, аналогичное полю в зазоре заряженного конденсатора. Отличие между этими полями заключается в том, что в уравнениях поля электрические и магнитные напряженности меняются местами. В частности, в заряженном круглом конденсаторе существует электрическая напряженность ( E z ^ 0 ) и отсутствует магнитная напряженность ( H z = 0 ) . В незаряженном круглом конденсаторе с магнитом существует магнитная напряженность ( H z ^ 0 ) и отсутствует электрическая напряженность ( E_z = 0 ) .

Известны эксперименты по обнаружению электрического поля между обкладками незаряженного конденсатора с магнитом [810].