Электромагнитное моделирование композита из проводящих сферических включений

Данная работа посвящена исследованию особенностей СВЧ-нагрева металлических порошков с размером частиц много меньше длины волны применяемого излучения. В работе [1] путём аналитических выкладок показано, что СВЧ-нагрев металлических немагнитных порошков может быть обусловлен магнитными потерями или, другими словами, возникновением у таких материалов отличной от нуля мнимой части эффективной магнитной проницаемости. В работах [24] представлены основные методы расчета эффективных диэлектрической или магнитной проницаемостей, основанные фактически на использовании моделей эффективной среды. В данной работе выполнен расчет эффективных диэлектрической и магнитной проницаемостей композита прямым методом без использования приближения эффективной среды.

ТЕОРЕТИЧЕСКАЯ МОДЕЛЬ

поглощение именно в скин-слое проводящих частиц. Предполагается, что несмотря на плотную упаковку между частицами нет прямого контакта, а все свободное пространство заполнено воздухом. Рассматривается случай, когда частицы выполнены из немагнитного материала.

Пусть падающая электромагнитная волна TE-типа распространяется вдоль оси x , ее вектор электрической напряженности направлен вдоль оси z . Показанная на рис. 1. область композитной среды (область компьютерного моделирования) в направлении координатных осей y и z ограничена двумя парами поверхностей, параллельных плоскостям xz и xy , соответственно. Расстояние между парами параллельных плоскостей, ограничивающих область моделирования, в точности равно диаметру частиц. Для данной геометрии векторы электрической и магнитной напряженностей на противолежащих поверхностях связанны периодическими условиями. В направлении оси x область моделирования имеет конечный размер. Таким образом, представленная на рис. 1 модель отвечает бесконечному в плоскости yz композитному слою, образованному периодически расположенными сферическими частицами.

В настоящей работе проводится численное решение дифференциального уравнения для электрической компоненты волны, имеющего следующий вид:

Vx д ( VxE ) - k 02

£ — i---- v     Ю£о ,

E = 0 ,

где e , ц , ст - локальные диэлектрическая проницаемость, магнитная проницаемость и проводимость соответственно, k ₀ = to / c - волновое число в вакууме, £ ₀ = 8.85 X 10 ^{— 12} Ф] м - электри-

Рис. 1. Модель упорядоченной структуры из проводящих сферических включений

ческая постоянная. Решение уравнения (1) в точках наблюдения внутри композитного слоя находится прямым численным методом конечных элементов с учетом граничных условий. Сетка разбиения на конечные элементы задается таким образом, чтобы размер ячейки был много меньше размера неоднородностей (частиц и пустот между ними), длины электромагнитной волны и толщины скин-слоя.

Используемый метод численного решения уравнения (1) позволяет учесть внутреннюю структуру композита, в том числе провести анализ зависимости электродинамических характеристик композита от размера частиц и расстояния между ними. Полученное в результате численного расчета распределение напряженностей электрического и магнитного полей используем для вычисления волнового импеданса:

Z (0) = iZ^ ctg(kfBd) = Z2.          (5)

Из (4), (5) получим следующие выражения для расчета эффективных параметров композита:

7 eff

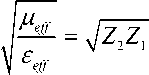
n eff

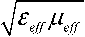
arctg (- Z 1 / Z 2) tod

Z (z) = -

Ey(z) Hx(z).

С другой стороны, в рамках приближения эффективной среды подобный композит можно рассматривать как макроскопически однородный материал с эффективными электрической и магнитной проницаемостями. В этом случае входной импеданс на границе z = 0 , на которую падает из внешней среды электромагнитное излучение, связан с эффективным импедансом Z fff = 7 K ff J ^£ eff следующим соотношением [5]

Z ( 0) = Z Z ( d ) iZefftg(keffd)

^H % - iZ ( d ) tg( kf_ffd ) ’ (3) где d - толщина слоя, k f = k ₀ 7E f Ц f . В настоящей работе эффективные параметры композита определяются с помощью (3) на основе значений импеданса для двух случаев. В первом слу-

чае на границе _z = d импеданс задается как для

идеального проводника, то есть принимается Z ( d ) = 0 , поэтому из выражения (3) приходим к следующему соотношению:

Z (0) = - iZ^ tg(k^d) = Z i. (4)

Во втором случае на границе _z = d импеданс задается как для идеального магнетика ( Z ( d ) = ~ ), поэтому входной импеданс для эффективной среды определяется как

РЕЗУЛЬТАТЫ РАСЧЁТОВ И ОБСУЖДЕНИЕ

С помощью выражений (6), (7) получены зависимости эффективных проницаемостей от размера частиц, объемной доли частиц и от частоты электромагнитного поля (рис. 2, 3, 4).

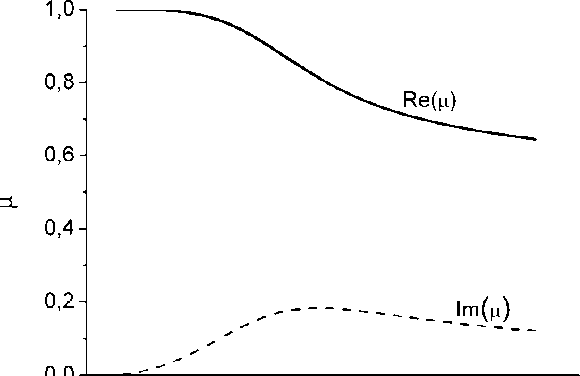
Из представленных на рис. 2 зависимостей видно, что эффективная магнитная проницаемость на частотах излучения, при которых радиус частицы r больше толщины скин-слоя массивного образца 5 = ^2/пшц 0 ( д ₀ = 4 я • 10 7 Гн/м – магнитная постоянная), принимает значения меньше единицы. С увеличением размера частиц действительная часть эффективной магнитной проницаемости Д = Re( Д. ^^ ) убывает, а мнимая часть Д = Im( д _е# ) становится отличной от нуля, достигая максимума около значения r / 5 = 2 , то есть когда толщина скин-слоя меньше половины радиуса частицы r . Данные результаты хорошо согласуются с результатами аналитического расчета по теории Ми и Бруггемана [3, 4].

Представленные на рис. 3 и рис. 4 графики позволяют установить следующие зависимости эффективных характеристик от параметров композита. Мнимая компонента эффективной магнитной проницаемости Д для широкого диапазона параметров композитной среды значительно превышает мнимую часть эффективной электрической проницаемости £ = Im( Д ^^ ) , поэтому основной вклад в электромагнитные потери дают магнитные потери. Действительная часть эффективной электрической проницаемости £ = Re( f ,f ) определяется концентрацией частиц ( £ ' повышается при увеличении объемной доли частиц), не зависит от частоты применяемого излучения (в рассмотренном диапазоне)

0,0 0,5 1,0 1,5 2,0 2,5 3,0 3,5 4,0 4,5 5,0

Рис. 2. Зависимость действительной и мнимой частей эффективной магнитной проницаемости порошка немагнитной меди от отношения радиуса частицы r к толщине скин-слоя 5 • Параметры расчета: объёмная доля частиц 0.5, проводимость q = 5.8 . 10 7 См / м

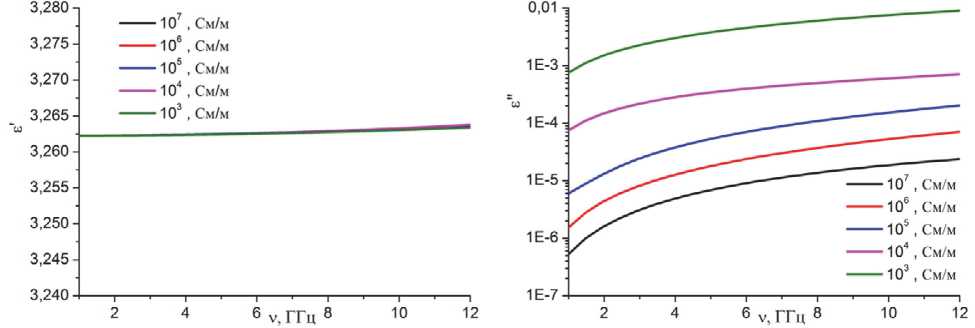
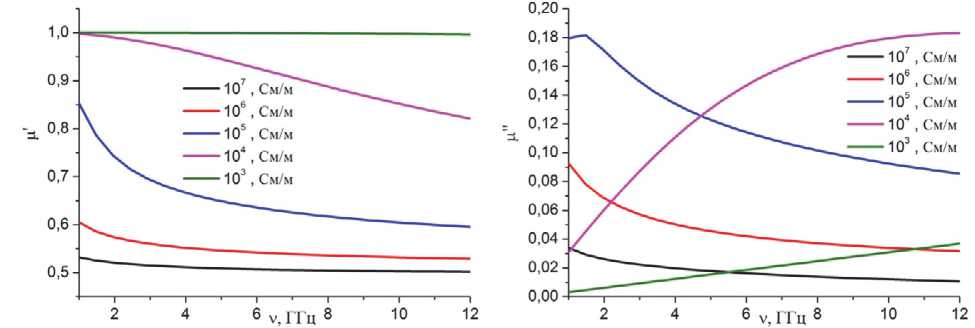
Рис. 3. Спектральные зависимости эффективных диэлектрической и магнитной проницаемостей композита для разной проводимости частиц. Параметры расчета: радиус частиц 100 мкм, объёмная доля частиц 0.39

и проводимости материала, из которого они выполнены. При увеличении объемной доли частиц и частоты излучения д уменьшается, а е" увеличивается. С увеличением проводимости частиц д и е* монотонно возрастают. Зависимость мнимой части эффективной магнитной проница- емости от проводимости имеет сложный характер, с ростом концентрации частиц д увеличивается. Таким образом, вклад магнитных потерь возрастает в композите с высокой концентрацией частиц, имеется также резонансная зависимость от частоты излучения в некотором интер-

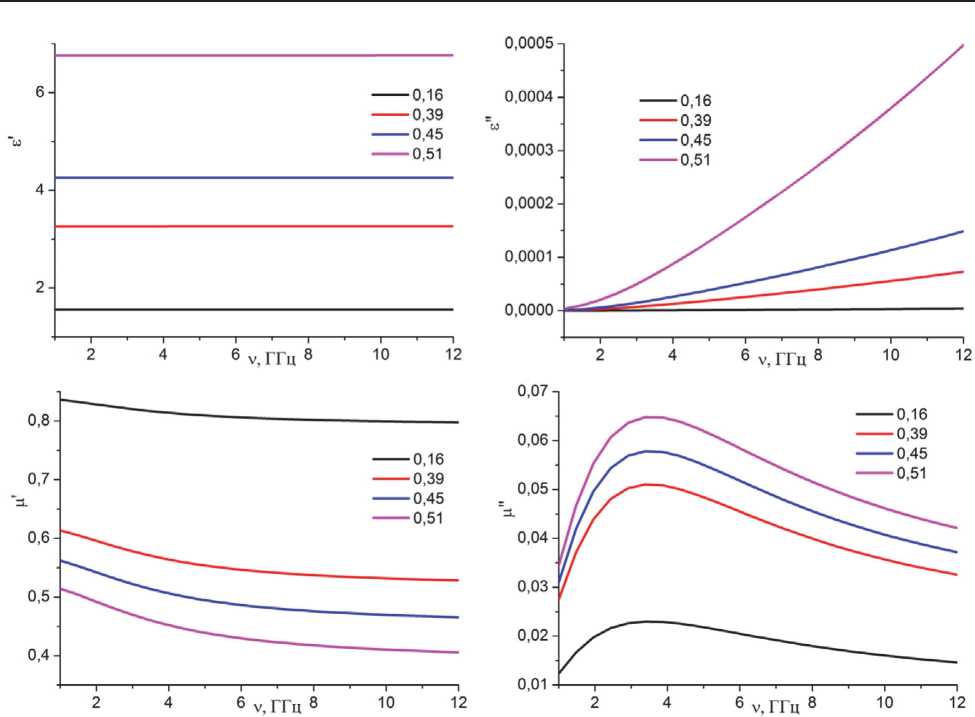
Рис. 4. Спектральные зависимости эффективных диэлектрической и магнитной проницаемостей композита для разной объёмной доли частиц. Параметры расчета: радиус частиц 100 мкм, проводимость частиц 1Q⁶ См / м

вале значений проводимости (см. зависимость ^(а ) на рис. 4).

ЗАКЛЮЧЕНИЕ

В настоящей работе получены частотные зависимости реальных и мнимых компонент эффективных диэлектрической и магнитной проница-емостей порошков из немагнитного металла. Показано, что даже в условиях отсутствия оболочки (окисного слоя) частиц мнимая часть магнитной проницаемости исследуемого композита значительно превосходит мнимую часть его диэлектрической проницаемости. Полученные результаты компьютерного моделирования подтверждают теоретические предсказания относительно преобладания магнитной составляющей в поглощении СВЧ-излучения скин-слоем немагнитных металлических частиц порошка. Появление у композитной среды из немагнитного металла комплексной эффективной магнитной проницаемости с отличной от единицы действительной частью связано с формированием в приповерхностном слое частиц замкнутых токов сферической геометрии и, соответственно, индуцированных магнитных моментов. Наблюдаемый эффект вы- ражен более сильно при определенных параметрах задачи, когда индуцированные токи имеют форму сферической оболочки, что наблюдается при толщине скин-слоя меньше радиуса частиц.

Работа выполнена при финансовой поддержке Российского фонда фундаментальных исследований и Федеральной целевой программы “Научные и научно-педагогические кадры инновационной России на 2009-2013 годы” Министерства образования и науки РФ.