Электромагнитные процессы в стационарном поле

1.    Основные формулы

Ранее нами было предложено описание фотопроцессов в импульсном поле с помощью следующего универсального выражения для полной вероятности, выведенного в рамках квантово-механической теории возмущений и дипольного приближения [1]

^ = 4^2 /“ ^Х ■ ■               (D

Здесь ег(ш) - сечение фотопроцесса, Е (ш)- фурье-образ напряженности электрического поля в импульсе, с - скорость света. В статье [2] это выражение было обобщено на недипольный случай для рассеяния электромагнитного поля. Данная работа посвящена описанию электромагнитных процессов в стационарном поле. Для этого введем корреляционную функцию напряженности электрического поля

KE_i3 (t',t"') = {Ei^Ej (t")).                                 (2)

• (с) Астапенко В. А., Кротов Ю. А., Сахпо С. В., 2025

• (с) Федеральное государственное автономное образовательное учреждение высшего образования

  «Московский физико-технический институт (пациопальпый исследовательский университет)», 2025

Здесь угловые скобки обозначают усреднение по состояниям поля, например, по абсолютной фазе излучения. В рассматриваемом случае стационарного поля корреляционная функция зависит только от разности времен т = t" — t':

KE_i3 &,{') = KE_i3 (т )

и не зависит от каждого из времен в отдельности согласно определению стационарности. Вероятность фотопроцесса при воздействии электромагнитного поля на сферически симметричную мишень в данный момент времени дается равенством [3]:

W = ^-2 ^ du ^ ) ^ dt'! dt''exp-—iw(t” — t’y) E^t') E^t’’),          (4)

где a(w) - сечение фотопроцесса, по повторяющимся индексам здесь и далее предполагается суммирование.

После усреднения по состоянию поля с учетом (3) формулу (4) после замены переменных можно переписать в виде

(W (t) =

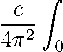
du

∞

дМ hw

‘ dt' /    dT exp(—iwT)КЕц(т ).

-∞   -∞

Поскольку стационарное поле не ограничено во времени, полная вероятность фотопроцесса (5) бесконечна. Поэтому в рассматриваемом случае актуальной величиной, описывающей фотопроцесс, является вероятность в единицу времени (или скорость) - w, которая определяется равенством w =

dW (t) dt

Подставляя (5) в (6), после несложных преобразований находим

W = Л Г dw^KE(i(U,                 (7)

l^2 0Q      пи где KEii(w) - Фурье-образ функции KEn(t), определенной равенствами (2)-(3).

Равенство (7) является обобщением формулы для скорости возбуждения дипольного перехода [4] на произвольный фотопроцесс.

Интересно сравнить выражение (7) с формулой для полной вероятности фотопроцесса в случае импульсного возбуждения за все время действия поля (1). Видно, что переход от (7) к (1) отвечает замене KE_ii(w) ^ |E(w)|².

Величина KEii(w) представляет собой спектральную плотность поля. Она может быть выражена через спектральную плотность энергии поля в единице объема р, которая определяется равенством

E/V = [ dwp(w),(8)

где E - энергия поля, V - объем, занимаемый полем. Несложно показать [5], что

KEn(w) = (2л)2р(и).(9)

Тогда формула (7) перепишется в виде w = —У dw^hU-L p(w') = j dwa(w)jph(w),(10)

где jph(w) = —p(w)/hw - спектральная плотность потока фотонов.

2.    Двухуровневая система в стационарном поле

Для дальнейшего выразим сечение фотопроцесса через нормированный спектральный профиль G(ш) (J G(ш)dш = 1).

а(ш) = atotG^atot = / a(ш)dш.

(И)

Как видно из второго равенства (И), величина a_tot представляет собой интегральное по частоте сечение фотопроцесса. В отличие от обычного сечения оно имеет размерность см² с.

Вывод выражения для коэффициента Эйнштейна В для вынужденного излучения

Поучительно с помощью полученных выражений вывести формулу для коэффициента Эйнштейна для вынужденного излучения.

В основополагающей статье А. Эйнштейна [6] предполагалось, что а(ш) = пы5(ш - шо),

где шо - собственная частота двухуровневой системы.

В случае двухуровневой системы интегральное по частоте сечение имеет вид [5]:

2х2е2

где /о ~ сила осциллятора перехода в двухуровневой системе. Подставляя формулы (12), (13) в (10), приходим к равенству w = Вр(шо),

где

2х2е2

—ё-во

тКшо

выражение для коэффициента Эйнштейна В через силу осциллятора [5].

Рассмотрим далее два различных предельных случая стационарного поля: тепловое (стохастическое) и монохроматическое (когерентное).

3.    Предельные случаи

Тепловое излучение

Спектральная плотность энергии теплового излучения в единице объема дается формулой Планка:

Рт(ш) =

^ш3

л²с³ ехр(Кш/Т ) — 1,

где Т - температура в энергетических единицах.

С учетом (16) получаем скорость фотопроцесса в поле теплового излучения atot Гл    G(ш)ш2

^Wт   6^3 с² J_o   ^ШехрЩ1ш/Т ) — 1.

Здесь сечение фотопроцесса записано в виде (И). В общем случае, когда ширина спектра теплового излучения много больше ширины спектрального профиля сечения у (Т/h >>  у), можно положить G(ш) ~ д(ш — шо)• Тогда из (17) получаем для скорости фотопроцесса, индуцированного тепловым излучением, следующее выражение:

w_T =

atot

6л³с² ехр(Кш_о/Т ) — 1.

Из данного выражения следует, что в пределе высоких частот ( Кшо >> Т) скороств фотопроцесса экспоненциалвно мала, а в противоположном пределе она линейно возрастает с температурой.

Монохроматическое излучение

В этом случае имеем для спектралвной плотности энергии поля с амплитудой Ео и частотой ш _с следующее выражение:

Е%.

Ртоп(ш) = Ж° ^ ( ш - Шс).

8Г

Подставляя (19) в (10), получаем w = a(uc)jph(wc), где jph(wc) = сЕ0/(8ггНшс) - плотноств потока фотонов монохроматического излучения на частоте шс с амплитудой напряженности электрического поля Ео. Отметим, что равенство (20) является определением сечения фотопроцесса.

4.    Фотоионизация тепловым излучением ридберговских состояний атомов

Используем формулы (10), (16) для описания скорости фотоионизации ридберговских атомных состояний тепловым излучением. Для сечения фотоионизации ридберговского состояния с квантовыми числами п, 1 и эффективным зарядом атомного остова Z_eff воспользуемся следующим выражением [7] в атомных единицах:

O_nl(u) =

32г ([+_l/2)Ze^

3^3    п³с ш ²

exp ^—

2 ш ( 1 + 1 / 2) 3 ^3Z2ff

)

Подставляя сечение (21) в формулу (10) и заменяя нижний предел интегрирования по частоте на ^_min = m_ee⁴/2п²Н³ (потенциал ионизации ридберговского состояния с заданным квантовым числом п), получаем скорость фотоионизации ридберговского состояния тепловым излучением как функцию температуры, а также квантовых чисел состояния и эффективного заряда атомного остатка.

Введем также в рассмотрение полную скорость фотоионизации уровня с заданным главным квантовым числом п, просуммированную по возможным значениям орбитального квантового числа и-1

wtot(n) = ^ w(n,l).                                (22)

l=0

Результаты расчетов скорости фотоионизации по формулам (10), (21), (22) представлены на рис. 1-4. Зависимость скорости фотоионизации ридберговского состояния от температуры показана на рис. 1 для п = Юи различных значений орбитального момента. Анализ показывает, что в области температур Т >  104К, функция w(T ) приближенно описывается «законом трех вторых»: w(T ) ~ Т ^3/2.

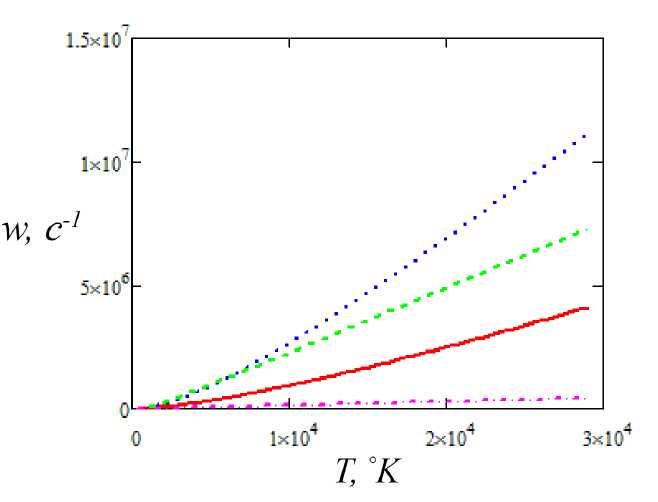
Рис. 1. Скорость фотоионизации ридберговского состояния тепловым излучением как функция температуры для п = 10, Z_eff = 1 и различных орбитальных моментов: сплошная кривая -1 = 0, пунктир -1 = 1, штриховая кривая -1 = 5, штрих-пунктир I = 9

Зависимость скорости w от орбитального квантового числа представлена на рис. 2 для различных значений температуры. Видно, функция w(l) имеет максимум, положение которого незначительно смещается в область малых I с ростом температуры.

2x10

1.5x10 - уц С1 ЫО7-

?<г-

°0

Рис. 2. Скорость фотоионизации ридберговского состояния тепловым излучением как функция орбитального момента для п = 10, Z_eff = 1 и различных температур: сплошная кривая - Т = 3160 К, пунктир - Т = 9480 К. штриховая кривая - Т = 31 600 К

Полная скорость фотоионизации как функция температуры представлена на рис. 3 для различных значений главного квантового числа ридберговского состояния. Видно, что для достаточно высоких температур данная функция близка к линейной.

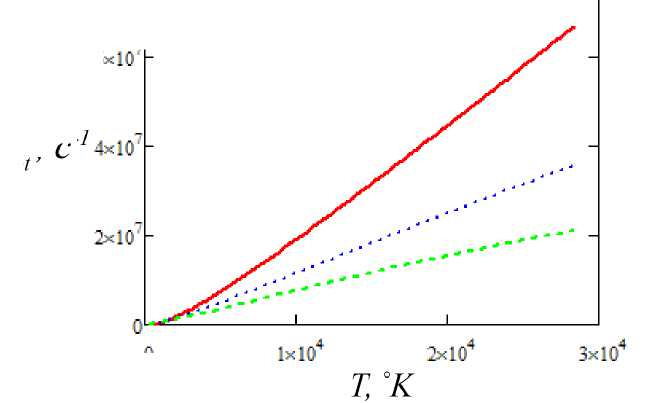
Рис. 3. Полная скорость фотоионизации ридберговского состояния тепловым излучением как функция температуры Z_eff = 1 и различных значений главного квантового числа: сплошная кривая - п = 10, пунктир - п = 15, штриховая кривая - п = 20

Зависимость полной скорости фотоионизации от главного квантового числа показана на рис. 4 для различных температур. Так же как и функция w(l) эта зависимость имеет максимум, смещающийся в область меньших значений п при увеличении температуры.

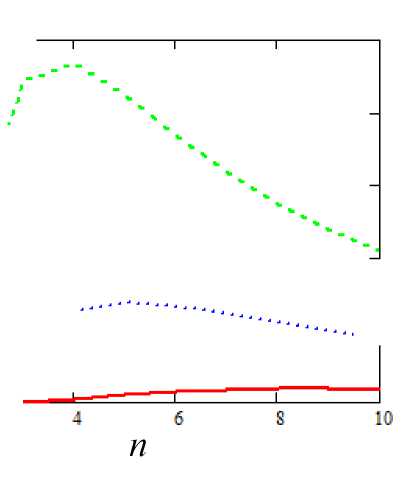
Рис. 4. Полная скорость фотоионизации ридберговского состояния тепловым излучением как функция главного квантового числа для Z_eff = 1 и различных температур: сплошная кривая - Т = 3160 К, пунктир -Т = 9480 К, штриховая кривая -Т = 18 960 К

5.    Заключение

В рамках квантово-механической теории возмущений получено универсальное выражение для скорости фотопроцесса в стационарном поле через сечение процесса и спектральную плотность энергии поля. С помощью полученной формулы продемонстрирован вывод выражения для коэффициента Эйнштейна В и рассмотрены два предельных случая стационарного поля: теплового излучения (стохастический предел) и монохроматическое поле (когерентный предел). Рассчитана скорость фотоионизации ридберговских состояний атомов тепловым излучением как функция температуры и квантовых чисел состояния.

Исследование выполнено за счет гранта Российского научного фонда № 24-49-10004, / project / 24-49-10004/