Электромеханические силокомпенсирующие системы подъёмно-транспортных манипуляторов

В различных отраслях промышленности для транспортировки заготовок и изделий к последующим технологическим операциям или для складирования применяются различные подъёмнотранспортные устройства и машины. Среди них можно выделить устройства, при работе с которыми оператору необходим контакт с перемещаемым объектом в процессе его движения и особенно при позиционировании. К таким устройствам можно отнести специальные грузоподъёмные устройства и сбалансированные манипуляторы (СМ), которые можно отнести к классу подъёмно-транспортных манипуляторов (ПТМ).

В качестве исполнительного привода в ПТМ применяют гидравлический, пневматический и электрический привод. Доступность и простота использования электрической энергии определила широкое распространение ПТМ с электроприводом [1, 2].

При креплении груза или объекта манипулирования в грузозахватном механизме его перемещение в рабочем пространстве ПТМ осуществляется с помощью электропривода (ЭП) при воздействии рукой на кнопки или рычаги управления скоростью двигателя. При этом другой рукой он может позиционировать объект в пространстве и перемещать по необходимой траектории.

Специальные грузоподъёмные устройства обычно реализуются с применением канатных передач и содержат барабан, на который наматывается канат с грузозахватным блоком и вместе с двигателем подвешивается к балке, вдоль которой может перемещаться [3]. В свою очередь балка может перемещаться по рельсам, проложенным на стеновых колоннах или опорах цеха, увеличивая тем самым зону обслуживания.

Сбалансированные манипуляторы и консольные грузоподъёмные краны конструктивно состоят из колонны, на которой располагается головка с исполнительным устройством рычажного типа. Головка с располагающимся в ней электродвигателем и устройством управления поворачивается относительно вертикальной оси колонны [2]. Такие манипуляторы более компактны и имеют радиальную зону обслуживания, что актуально на операциях перегрузки объектов.

Обобщённые требования

Анализ и обобщение требований к рассматриваемым грузоподъёмным устройствам и механизмам позволяет выделить среди них манипуляторы, применение которых в промышленности определяется следующими техническими характеристиками:

– грузоподъёмность

– скорость вертикального перемещения

– скорость горизонтального перемещения

– ускорение

– высота обслуживания

– угол поворота

– радиус обслуживания до 1000 кг;

от 0,03 до 0,5 м/с;

до 0,33м/с;

до 2 м/с2;

до 3,2 м;

до 360°;

до 4 м.

Выполненный анализ технических характеристик и функциональных возможностей позволяет отметить преимущества ПТМ:

• -    отработка сложных траекторий перемещения объекта при непосредственном воздействии на него оператора;

• -    возможность плавного изменения скорости перемещения объекта;

• -    плавное перемещение объекта из позиции в позицию и точная остановка его в заданной точке при движениях на малых скоростях.

Существующие способы управления

Качественное и надежное функционирование ПТМ во многом определяется конструкцией механизмов перемещения и системой управления исполнительного привода, который должен обеспечивать возможность плавного изменения скорости манипулятора без рывков, вибраций и просадок объекта, а также ограничение ускорения привода в пуско–тормозных режимах с целью снижения динамических нагрузок в его механической части.

В зависимости от требований технологического процесса, который обслуживает ПТМ, а также от функций и операций, выполняемых системой управления, их исполнительные приводы реализуют различными способами.

Наиболее простым способом является управление исполнительным приводом ПТМ при перемещении объекта с фиксированной скоростью [1]. В этом случае пуск и торможение электродвигателя сопровождается повышенными колебаниями объекта, что обуславливает необходимость снижения рабочей скорости его перемещения. Применение нерегулируемых электроприводов оправдано для ПТМ с достаточно большой зоной обслуживания при отработке прямолинейных траекторий, когда соударение при перемещении с другими объектами исключено.

Использование в ПТМ асинхронного ЭП обуславливает ряд дополнительных требований к системе управления. При наличии активного момента нагрузки на валу двигателя требуется применение однонаправленной силовой передачи от двигателя к объектовому блоку манипулятора, что обуславливает значительное увеличение тепловых потерь в двигателе, выделяющихся при использовании параметрического способа регулирования скорости [5]. Снизить колебательность перемещаемого объекта в пуско-тормозных режимах позволяет использование для управления асинхронным электродвигателем устройства плавного пуска, которое уменьшает рывки и просадки объекта в процессе перемещения. Однако применение устройства плавного пуска в системе электропривода ПТМ не позволяет длительно регулировать скорость перемещения объекта.

При необходимости движения объекта по сложным траекториям в электромеханической системе современных ПТМ часто применяются частотные преобразователи. Они позволяют плавно регулировать скорость вращения электродвигателя исполнительного механизма в широком диапазоне и обеспечивают при этом требуемую динамику при перемещении объекта в режимах пуска и торможения [5, 6].

Анализ способов построения и реализации систем управления ПТМ показал, что задачей управления в существующих манипуляторах в основном является регулирование скорости, а настройка их систем управления чаще всего осуществляется по показателям переходного процесса, вызванным изменением управляющего воздействия [1]. Скорость перемещения и траектория движения объекта задаётся воздействием на устройства управления двигателя исполнительного механизма, поэтому при функционировании ПТМ возможны колебания в упругих элементах их механической части. Это повышает сложность управления манипулятором при необходимости точного позиционирования объекта, что в итоге приводит к снижению производительности [5].

Предлагаемый способ управления

Система вертикального перемещения ПТМ может быть реализована с использованием в системе регулирования информации об усилии в устройстве подвеса объекта, его весе и внешних силовых воздействиях, прикладываемых к нему для перемещений [7, 8]. При этом двигатель должен развивать усилие, равное весу объекта, но противоположное по направлению. Для реализации таких систем необходимо иметь информацию о динамических нагрузках исполнительных механизмов, что требует применения высоконадёжных в эксплуатации датчиков измерения усилий и реализации в системе управления дополнительных контуров обратных связей. Такой способ управления нашёл широкое применение при создании силокомпенсирующих систем тренажёров для подготовки космонавтов и испытаний изделий космической техники [9–11].

Возникающие при этом упругие колебания исполнительного механизма и динамические нагрузки в механизмах ПТМ ограничиваются с помощью ЭП. Это становится возможным благодаря созданию с помощью электродвигателя дополнительного силового воздействия, определённым образом взаимодействующего с моментом в упругих элементах (УЭ) механических передач манипулятора [12]. В системах, обеспечивающих компенсацию статической нагрузки объекта, можно отметить ряд достоинств:

• –    удержание объекта на весу без применения тормоза;

• –    отсутствие блока задания скорости;

• – возможность значительного уменьшения усилия оператора при перемещении объекта;

  – точность позиционирования объекта при реализации такой системы управления зависит только от действий оператора.

Таким образом, система регулирования электропривода должна обеспечивать с высокой точностью поддержание в элементах исполнительного устройства усилия, равного силе тяжести, при различных прикладываемых к объекту силовых воздействиях при манипулировании.

Реализованная таким способом система регулирования усилий (СРУ) позволяет осуществлять перемещения обезвешенного объекта в вертикальной плоскости за счет прикладываемой к нему незначительной силы F _в , создаваемой оператором. В этом случае задача электропривода механизма вертикальных перемещений заключается только в компенсации веса объекта и сил сопротивления его движению. Поэтому перемещение объекта в вертикальной плоскости будет определяться ошибкой регулирования усилия 5 _у, для минимизации которой необходимо решить задачи выбора рациональной структуры системы регулирования и синтеза параметров управляющих устройств. Обоснование рациональной структуры системы управления усилиями исполнительных механизмов сбалансированных манипуляторов приведено в [2, 13]. Для этого необходимо использовать соответствующее математическое описание электромеханической системы ПТМ.

Математическая модель

Динамические свойства двухмассовой электромеханической системы (ЭМС) регулирования усилий можно исследовать с использованием математической модели, структурная схема которой приведена на рис. 1 [2, 14]. Здесь обозначено: TД , TM – механические постоянные времени инерционных масс двигателя и объекта, разделенных упругим элементом; Tc , Td – постоянные времени, учитывающие эквивалентную жесткость и диссипативные свойства механических передач; Од , Ом - угловые скорости двигателя и объекта; EП , EД – ЭДС преобразователя и двигателя; M0 = Ро р - постоянная составляющая момента на валу двигателя, обусловленная весом Ро объекта; M, = К, р - момент, вызываемый внешними воз-вв мущающими силами Fв, прикладываемыми к объ- екту; Mд , Mтр, Mу = Ку р - моменты двигателя, трения и в упругом элементе; Fу – усилие в упругих элементах механических передач; ρ – радиус приведения; kэ , Tэ – коэффициент передачи и электромагнитная постоянная времени двигателя; kE , kДТ – коэффициенты передачи обратной связи по противоЭДС двигателя и датчика тока; kе, Те - коэффициент усиления и постоянная дифференцирования положительной обратной связи по ускорению двигателя; WxE (S), WдУ (S), WPy (^), WPT (^), Wn (^) - передаточные функции канала компенсации противоЭДС двигателя, датчика усилия, регулятора усилия, регулятора тока и преобразователя напряжения соответственно; Uоу , Uот , Uе , UкЕ - сигналы обратной связи по усилию в упругом элементе, току, ускорению и ЭДС двигателя, пропорциональные силе тяжести объекта; Uз – сигнал задания на стабилизируемое усилие.

Параметры структурной схемы представлены в относительных единицах: скорости О д и O M определяются в долях от скорости холостого хода двигателя О _о , ЭДС Е _П и Е д - от номинального напряжения двигателя, а моменты M _Д , M _у , M ₀ и M _в – от номинального момента двигателя M _н .

Базовые значения задающего напряжения U _зБ и напряжения датчика тока U _ДТБ выбраны так, чтобы статический коэффициент передачи цепи обратной связи по току был равен единице. Использование относительных единиц позволяет обобщить результаты исследований и упростить его, так как к_Е = к д_Т = к д = k _м = 1. При выбранных базовых значениях координат ЭМС имеем:

Т д = J д О о M - ¹; T m = J м О о M - ¹;

T = c у ^{- 1} О о M н ; T d = b у c - ¹,

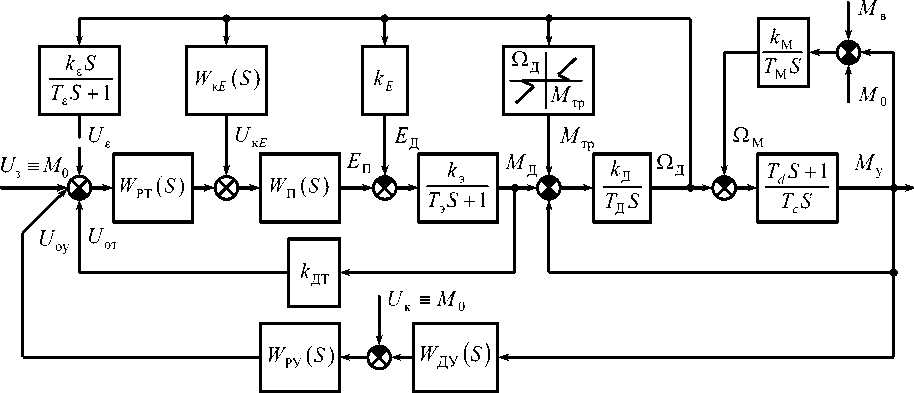
Рис. 1. Структурная схема ЭМС регулирования усилий в исполнительных механизмах ПТМ

где J _Д , J _M – моменты инерции двигателя и объекта; c _у , b _у – коэффициенты, учитывающие экви-

валентную жесткость и внутреннее вязкое трение механических передач.

Качество управления в исследуемой системе будем оцениваеть по ошибке регулирования усилия S у и силе (моменту) трогания объекта F _Tpor [15]:

⁵ у

А М У

M В

1 +    T M

^Т Д k кт k е

т M v (1 ⁺ k ру k ДУ k кт ) ^{+ 1}

^ТД k КТ k е

; (1)

M

M трог = ^ трог Р = ,  ,    , р ,    ,             (2)

¹ k РУ k ДУ k КТ

где k _РУ , k _ДУ , k _КТ – коэффициенты передачи ре-

гулятора усилия, датчика усилия и замкнутого контура регулирования тока; k ε – коэффициент передачи обратной связи по ускорению, наличие которой приводит к уменьшению влияния механической постоянной электродвигателя, а также к улучшению демпфирующих свойств системы. Предельные значения коэффициента k _ε предлагается определять исходя из условий устойчивости ЭМС с УС. По рекомендациям, приведенным в [18]:

k е ^{- Т} Д П К КТ . ⁽³⁾

Для обеспечения требуемого качества функционирования электромеханической системы ПТМ решим задачу синтеза регулятора усилия, который, осуществляя параллельную коррекцию ЭМС, обеспечит требуемое качество переходных процессов в исследуемой системе регулирования.

раничения, накладываемые на управляющее воздействие, случайный характер возмущающего воздействия, устойчивость синтезируемой системы управления к изменению параметров объекта. Синтез оптимального регулятора усилия будем осуществлять в линеаризованной ЭМС с учетом следующих допущений:

• –    влияние ЭДС двигателя полностью скомпенсировано каналом с передаточной функцией W e ( ^ ) = k E/ W n ( $ ) ;

• –    свойства замкнутого контура регулирования тока аппроксимированы апериодическим звеном первого порядка W _кт ( S ) = к _кт /( Т _кт S + 1 ) ;

• –    каналы измерения усилия и ускорения безынерционные с передаточными функциями W . ( $ ) = к ДУ , W _E( $ ) = к е .

Составляющая момента двигателя M ₀ , определяемая весом объекта, постоянна, поэтому при синтезе регулятора усилия будем рассматривать задачу минимизации отклонения в упругом элементе А М У , вызываемого изменением внешнего возмущения А М В .

Введем обозначения:

^ТД ⁺ T M .

^т дэ ⁺ T M

ДЭ + М . р 1 гр .Г TДЭ

T М

^Т дэ ^{+ Т} М

;

Т = ^у

Т т т

T _Д T _М T_c

^Т дэ ⁺ T M

T

Ц = —,

T _ДЭ

Синтез оптимального регулятора усилия

Анализ технической литературы по исследуемой проблеме показал, что решение задачи синтеза целесообразно осуществлять с использованием методов оптимального управления, основанных на вариационном исчислении [16, 17]. При решении этой задачи необходимо учитывать реальные ог-

где Т дэ = Т д - к _КТ к _е - значение эквивалентной механической постоянной времени двигателя в системе с обратной связью по ускорению двигателя.

С учетом принятых выше допущений исходную структурную схему СКС подъёмно-транспортного манипулятора (см. рис. 1) для решения задачи синтеза оптимального регулятора усилия представим в виде, приведенном на рис. 2 [15].

Согласно структурной схеме, приведенной на рис. 2, момент в упругом элементе можно определить по выражению:

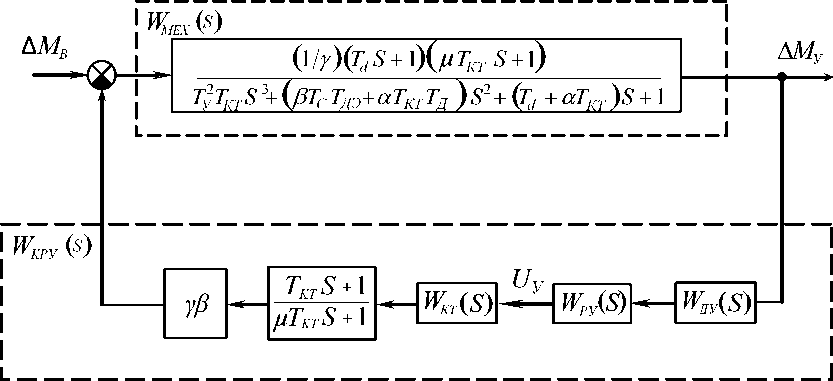
Рис. 2. Структурная схема СКС ПТМ

KMу (S) = A UУ (S) W (S) + AMв (S) Wye (S), (4) где Wyy (S) и WyB (S) - передаточные функции системы регулирования по управляющему и возмущающему воздействиям при разомкнутой обратной связи по усилию; ΔUУ – сигнал управления на выходе регулятора усилия.

С учётом принятых обозначений определим

W yy ( S ) =

A M _y ( S ) A U _y ( S )

________________ ( T d S + 1 ) к кт P ________________

T y T T S ³ + ( ₽ T_cT p + а Т кт Т д ) S ² + ( T d + a T ) S +1

; (5)

W b ( S ) =

A M _y( S ) A M b ( S )

=____________ ( 1 Y )( T d S + 1 )( ц Т кт S + 1 ) ____________

T y T KT ^{S 3 +} ( ^P T C T ]3 ^{+ a T} KT T ] ) ^{S 2 +} ( T d ^{+ a T} KT ) ^{S + 1}

Синтезируемое управляющее воздействие, подлежащее определению, будет описываться вы- ражением

A U _y ( S ) = k _]y W _py ( S ) A M _y ( S ) .         (7)

Подставив в уравнение (4) передаточные функции (5) и (6), получим:

A ( S ) A M _y ( S ) = B ( S ) A U _y ( S ) + C ( S ) A M _в ( S ) , (8)

где A ( S ) = a ₃ S ³ + a ₂ S ² + a 1 S + a 0 , B ( S ) = b 1 S + b 0 ,

C ( S ) = c ₂ S ² + c 1 S + c ₀ ;

a3 = Ty TKT , a2 = P ТСТДЭ + aTKTТД , a1 = Td + a TKT , a 0 = 1 ;

b = ^{P T}d^k KT , ^b 0 = ^{P k} KT ^;

c 2 = T KT T d ц/Y , c = ( ц T KT + T d )/y , c о = V Y .

Уравнение (8) с учетом управляющего воздействия (7) описывает поведение замкнутой системы регулирования усилия, в которой необходимо определить структуру и параметры передаточной функции регулятора Wpy (S). Для решения задачи синтеза оптимального регулятора Wpy (S) в соответствии с требованиями функционирования ПТМ необходимо минимизировать средний квадрат (дисперсию) отклонения момента в упругом элементе за время работы tр системы. Тогда при наличии ограничения, накладываемого на мощность управляющего воздействия AUy, критерий качества управления запишем следующим образом:

1 t _p

J = lim — f ( m ² A M y +A U y ) dt , t p ^“ t p 0 ^{V                   7}

где A M _y =P k _KT A U _y ; m ² = 1/ X ( p k _KT k д_У ) ; A - коэффициент Лагранжа.

Определим передаточную функцию регулято- ра усилия Wpy (S), который доставляет минимум функционалу (9).

При оптимизации ЭМС по квадратичным критериям при вариации параметров объекта управления может возникнуть проблема потери устойчивости системы, поэтому при минимизации функционала (9) необходимо рассматривать не произвольные вариации комплексного коэффициента передачи Wpy (jго), как обычно делается в вариационном исчислении, а лишь вариации, совместимые с устойчивостью исследуемой системы. Для гарантированного обеспечения устойчивости данной ЭМС с оптимальным регулятором введём дополнительные полиномы a (S) и b (S) так, чтобы полином Q(S) = A(S) a(S) + B(S) b(S) был Гурвицевым [13]. Исследования показали, что в рассматриваемой системе управления ПТМ это условие будет выполняться при a (S) = 0, b (S) = 1, что соответствует Q (S ) = B (S).

Для определения свойств объекта и управляющего воздействия, описываемых полиномами A ( S ) и B ( S ) , с учетом ограничения, вводимого с помощью коэффициента m 1 ² = 1) Х = m P k _KT k д_У , факторизуем полином:

A (S) A (- S) + m2 B (S) B (-S) = x6 + z4x2 + z2x + z0 = G (S) G (-S),        (10)

где

a 2 - 2 a ₃ a 1

z 4 =        2       ;

a ₃

z 2 =

a 1 + m 1 b 0   2 a 2 a 0

a

z 0 =

a 2 + m 2 b 0

a

Корни уравнения (10) можно вычислить на ПЭВМ или определить с помощью следующих аналитических формул:

z 4 1          _ I z 4 I p =---+ z? ; q = 2 —

3     2 I 3 J zz

4^2 + + z

0 ;

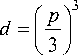
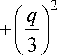
; d = 3i

q + dd ;

L = 3 - q - V d ; x ₂ =±. D + L - z ⁴ ;

2           1,2

x 3,4,5,6

I D + L z ₄ , ,D - L

Л I ----± j------

Tогда коэффициенты полинома G ( S ) будут равны: g 3 = a 3 = T y T KT ^; g 2 = ^ga3 = gT y ^T kt ^;

g ² a 2 + 2 aa - a 2

g 1 =--------;

2 a ₃

g 0 = V m ² + ¹;

g = x2 + Re [ x4 ] , где x2 , x4 – корни уравнения (10), находящиеся в левой полуплоскости.

Выполнив преобразования исходной математической модели с учётом уравнений (7, 8, 10), найдем передаточную функцию оптимального регулятора усилия для исследуемой ЭМС:

W „ ( s ) = -    y ^{2 5} 2 + y 1 ^{S +} y 0   ,        (11)

' '    ( T d 5 + 1 )( Т зн s + к ЗН)          ¹ '

где y2 = t2 + g2 t- ТУ [a TKT ( Тдэ Td + Ткт Тд ) +

^{+ Т} ДЭ ⁽P ^Tc ^- g 2 ^{) -} g 1 ^Т Д ^Т КТ J ;

y l = ^{( T}d ^{+ a Т} КТ ) ( t ^- g 2 ^Т Д ) ^{+ (} g 0 ^- 1 ) ^Т У ^Т Д ^Т КТ ⁺

^{+ (} g l ^{-a- T}d ) ^ТУ ^Т дэ^;

y 0 = t ^{+ (} g 0 ^{- 1 ) Т} У ^Т ДЭ ^- g 2 ^Т Д ^;

t = ^{a T} d ^T KT ^Т д ⁺ P ^Т с ^Т д ^Т дэ ^{; Т} зн = ^Т д ^Т кт ^Ту ^;

^к ЗН = ^Т У ^ТДЭ ^- t ⁺ g 2 ^Т Д .

Анализ выражения в числителе передаточной функции (11) показал, что его корни при реальном изменении параметров системы регулирования усилий всегда отрицательные вещественные. Знак минус в выражении (11) указывает на то, что обратная связь по моменту в упругом элементе должна быть отрицательной. Тогда передаточную функцию регулятора усилия можно записать в виде:

TS +1) ( T₂S +1

WPy(S) = kp y(^   )P   ),(12)

^{РУ (} ) ^РУ ( T₃S +1) T5 +1)

где kРУ = - —-----------Г;

( ^T y ^Т ДЭ ^- t ⁺ g 2 ^Т Д ) P k КТ ^k ДУ

2 y ₂

У 1 ⁺ V У 1 ^{2 - 4} y 2 y 0

2y2;

• ^{- y}1 ⁺ 7 ^y1 ^{- 4 y} 2 ^y 0

Т зн =     ^Т Д ^Т зн ^Т у    _{; T} = _T

• ^k ЗН   ^Т У ^Т дэ ^- t + g 2 ^Т д

Исследования системы с оптимальным регулятором

На примере сбалансированного манипулятора типа МП-100 грузоподъёмностью 100 кг выполним синтез параметров системы управления усилиями, которая должна обеспечить ошибку регулирования усилия 6 _у = 0,05, момент трогания M _трог = 0,003. Математическая модель исследуемой ЭМС имеет следующие параметры неизменяемой части: Т Д = 0,1с; Т М = 0,01с; T_d = 0,0015с; Т с = 0,2с; Т кт = 0,002с; к кт = к ду = 1; M б = M _н; О Б = Q ₀ ; M _тр = 0,4 . Исследования выполним при значении внешнего возмущающего воздействия M в = 0,1.

По выражению (2), с учётом требуемого момента трогания M _трог = 0,003, определим необходимый коэффициент усиления регулятора усилия к _РУ = 129, при котором обеспечивается заданный момент трогания. Ошибка регулирования усилия S у при к _РУ = 129 в соответствии с выражением (1) будет равна 0,05. По полученным значениям k _РУ и выражениям (11), (12) при значении коэффициента m 1 = 16, учитывающего энергетические ограничения электропривода, при котором к _РУ = 129, определяем параметры регулятора усилия:

0,0073 5 + 1) (0,0095 5 + 1)

Wp _у( S ) = 129 ( ,         )>^          ) .

• ^РУ^ ’      ( 0,0020 S + 1 )( 0,0015 S + 1 )

Эффективность предложенного управления в исследуемом манипуляторе проиллюстрирована на рис. 3, где приведены графики переходных процессов моментов в упругом элементе A M _у и двигателе A M д в системе регулирования с главной обратной связью по скорости ( 1 и 3 ) и в системе регулирования усилий при к _РУ = 129 ( 2 и 4 ).

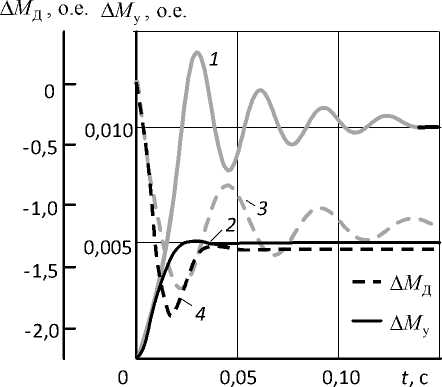
Рис. 3. Графики переходных процессов Д М д ( t ) и Д М у ( t ) при различных способах управления манипулятором МП-100

Анализ графиков, представленных на рис. 3, показывает, что использование в качестве системы управления механизма вертикальных перемещений сбалансированного манипулятора МП-100 системы управления усилиями и синтезированного регулятора (12) позволило существенно повысить качество функционирования манипулятора.

Заключение

Выполненные исследования позволили определить преимущества применения подъёмнотранспортных манипуляторов с предложенной силокомпенсирующей системой управления:

• 1)    возможность приложения незначительных усилий оператора для перемещений объекта;

• 2)    осуществление активного демпфирования колебаний с помощью ЭП, возникающих при манипуляциях;

• 3)    повышение производительности работы манипулятора, так как требуемая скорость перемещения и позиционирование объекта определяется непосредственно руками оператора.

Использование предлагаемого способа управления ПТМ при перемещении объектов особенно актуально:

• 1)    при работе с крупногабаритными объектами, размеры которых затрудняют обзор при позиционировании и требуют участия сразу нескольких человек;

• 2)    при манипуляциях с хрупкими объектами, где важна плавность скорости их перемещения с точки зрения производительности и сохранения целостности объекта;

• 3)    при перемещениях объектов с частым изменением направления движения в пространстве ввиду наличия различных препятствий на траектории перемещения.

Работа выполнена в рамках базовой части государственного задания 2014 года при поддержке проекта № 2878 «Развитие теории и практики создания электротехнических систем тренажерных комплексов и мобильных объектов».