Электромеханические системы космических аппаратов и автоматизация их проектирования

Проблематика автоматизации проектирования электромеханических систем космических аппаратов

Электромеханические системы (ЭМС) для космических аппаратов (КА) проектируются [1–6] как совокупность взаимосвязанных модулей, среди которых можно выделить электродвигатель (ЭД), механическое преобразовательное устройство (МПУ, например редуктор), электропреобразовательное устройство (ЭПУ, например транзисторный коммутатор), измерительные устройства (ИУ, например датчики углового положения, тока и др.), а также управляющее устройство (УУ). При этом ЭД, МПУ и ЭПУ выбирают на этапе силового проектирования ЭМС, а ИУ и УУ – на этапе проектирования контура управления.

Проектирование современных ЭМС КА предпочтительно выполнять с помощью автоматизированного рабочего места (АРМ) электромеханика, которое включает в себя техническое, программное, математическое и методическое обеспечение.

Работы по созданию АРМ такого назначения ведутся параллельно в научно-учебной лаборатории систем автоматизированного проектирования (НУЛ САПР) СФУ и в ОАО «Информационные спутниковые системы имени академика М.Ф.Решетнёва» (ОАО ИСС).

АРМ электромеханика в НУЛ САПР создаётся на базе аппаратуры International Instruments в сочетании с программным обеспечением LabView. Технической основой АРМ является аппаратно-программный комплекс, включающий автоматизированную экспериментальную установку с управляющим компьютером и отдельный компьютер для выполнения расчётов, объединённые через сеть в единую систему.

На первом этапе проектирования, называемом концептуальным, определяются: тип и принцип построения ЭМС – следящая, программного управления, стабилизации, разомкнутая, замкнутая (по каким координатам); тип УУ – микропроцессор, аналоговые устройства на операционных усилителях или др.; тип ЭД и способ управления им; отсутствие или наличие МПУ (и его тип при наличии); тип ЭПУ. Принятие одного частного проектного решения часто влечёт за собой возможность или необходимость принятия других конкретных решений. Обычно проектирование осуществляется с учётом накопленного опыта разработчиков, но возможна формализация этого этапа. Тогда при создании концептуальной модели для каждого элемента выделяют все его свойства, которые влияют на конечные показатели проектируемого ЭП или на выбор другого элемента. Например, выбор ЭД переменного тока малой мощности приведёт к выбору того или иного типа полупроводникового инвертора, который могут иметь различные схемные реализации. А выбор транзисторного мостового коммутатора приводит к тому, что схема соединения трёхфазных обмоток будет “звезда без общего провода” или “треугольник”, но не “звезда с общим проводом”. Выбор высокоскоростного ЭД приводит к выбору механического редуктора с большим передаточным числом, а выбор индукторного двигателя – с малым. Исходные данные задаются в виде таблицы смежности, являющейся формой представления графа. Такие цепочки технических решений строятся затем автоматизированно: в некоторых случаях возможен автоматический выбор последующего варианта, а в некоторых – требуется участие проектировщика. В результате решается задача анализа проектных решений в процессе их принятия. В настоящее время предполагается увеличить долю автоматического выбора, чтобы обеспечить возможность постановки и решения задачи концептуального синтеза.

Следующий этап проектирования структурный, на котором конкретизируются принятые ранее концептуальные решения по выбору элементов и их функционированию, а также разрабатывается их укрупнённое математическое описание и проверяются основные обобщённые соотношения по силовым, точностным и динамическим показателям технического задания. Для каждого концептуального решения создаётся библиотека структурных моделей, которая может наращиваться в процессе получения опыта проектирования и эксплуатации готовых ЭМС. На этом этапе для каждой выбранной структурной схемы разрабатывается своя методика расчётов требуемых показателей, и лучше всего для этих целей применимы универсальные математические пакеты программ типа Matlab, MathCAD, Maple. Методики синтеза привязаны к структурным схемам ЭМС и могут быть задействованы автоматизированно после осуществления автоматического структурного синтеза. Пока разработаны методики для трёх вариантов ЭМС с индукторным двигателем двойного питания, и работа продолжается. На этапах – 192 – функционального и поэлементного проектирования требуются ещё более детализированные модели.

В настоящее время ЭМС для систем поворота антенн и солнечных батарей КА проектируют на основе шаговых двигателей, синхронных двигателей с постоянными магнитами и индукторных двигателей различного типа (в некоторых случаях используется дополнительное возбуждение от постоянных магнитов, а также схема двойного питания). Такое разнообразие ЭД порождает большое разнообразие их математических моделей, которые до последнего времени разрабатывались вручную. В настоящее время существует возможность автоматизировать не только использование моделей при расчётах, но и процесс получения самих моделей, применяя символьные процессоры математических программ типа Matlab, MathCAD, Maple и др.

Методика автоматизированного получения комплекса математических моделей электродвигателей

Проектирование ЭМС КА основывается на использовании комплекса математических моделей соответствующих элементов, среди которых наиболее важны модели ЭД, устройства электропитания и механической части, включающей редуктор (если он есть) и механическую нагрузку. Наиболее многообразны математические модели ЭД, так как на разных стадиях проектирования для различных целей они необходимы в различном виде. Существующие методики получения математических моделей предусматривают ряд преобразований (рис. 1), которые в технической литературе обычно приводят для конкретных вариантов ЭД. Ниже эти преобразования представлены в более общем виде, пригодном для реализации в математических пакетах с использованием символьных процессоров.

Модель двигателя дополняется моделью механической нагрузки, которая в простейшем случае имеет вид уравнений механического равновесия:

^- j [ M ( , )+ M s, ( , > ] ;

■ (,)■                     J где tor - угловая скорость ротора; M - электромагнитный момент; Mst - момент нагрузки; J -момент инерции всех вращающихся масс, приведённый к валу двигателя.

Эта модель обычно рассматривается отдельно от модели ЭД, но в ряде случаев (например, при получении передаточных функций) обе модели рассматриваются совместно.

С использованием электрической схемы замещения, учитывающей конфигурацию обмоток, записывается система уравнений электрического равновесия в нормальной форме обыкновенных дифференциальных уравнений при раздельном питании обмоток:

d*« —R-i( t) + u( t), dt где v — вектор-столбец потокосцеплений обмоток; R - диагональная матрица активных сопротивлений обмоток; i - вектор-столбец токов обмоток; u - вектор-столбец питающих напряжений; t – время.

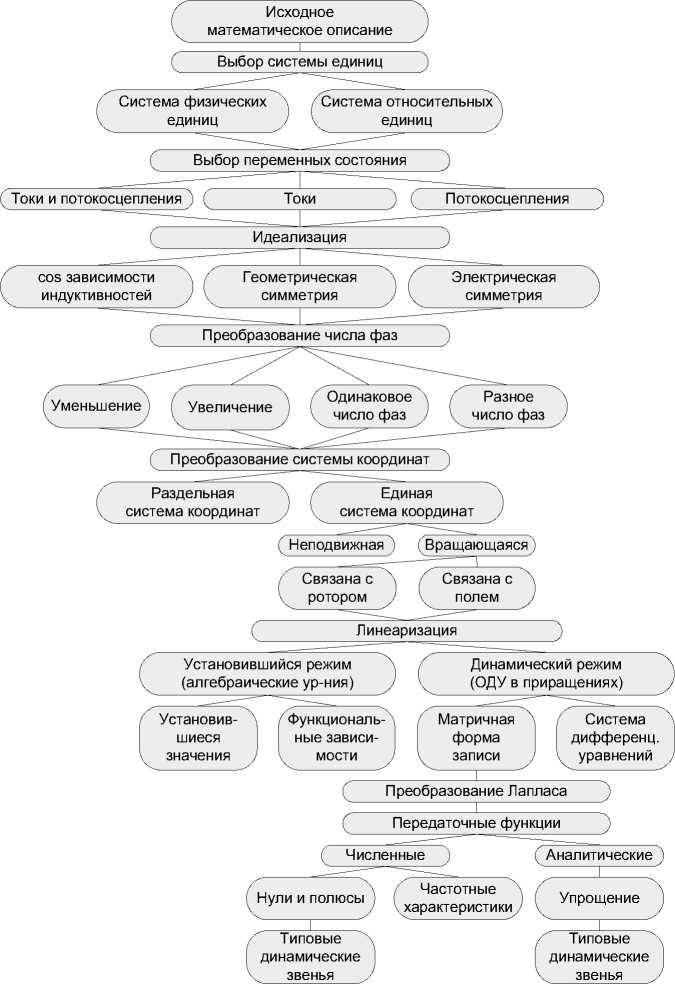
Рис. 1. Структурная схема процесса преобразования математических моделей

Связь между током и потокосцеплением в общем виде для ЭД с электромагнитным возбуждением и возбуждением от постоянных магнитов такова:

V [er (t )]=L[e r (t )]• i( t)+vJe r (t)], где L – матрица индуктивностей (собственных и взаимных); потокосцепление ψ показано как функция угла поворота θr, зависящего от времени; ψμ – вектор потокосцеплений постоянных магнитов с соответствующими обмотками.

Электромагнитный момент

2 L 50r J 2 [ 50r где индекс T обозначает транспонирование.

Преобразование числа фаз выполняется с использованием матриц прямого и обратного преобразования. Матрица прямого преобразования после умножения на неё вектора каких-либо переменных производит преобразование от действительного числа фаз к желаемому. Как правило, в литературе описано преобразование многофазных обмоток к двухфазным. Но в общем случае может потребоваться преобразование любого действительного числа фаз к любому другому – этот вариант не рассмотрен в литературе и изложен ниже.

Матрица преобразования числа фаз в общем виде:

П = w=

cos( 9 w U)	cos( 9 w 1,2 )		cos( 9 w 1, n )
cos( 9 w 2,1 )	cos( 9 w 2,1 )		cos( 9 w 2, n )
K	K	K	K
cos( 9 wm ,1 )	cos( 9 wm ,2 )		cos( 9 wm , n ^ ,

где 9 wj ,_к - углы между j -той действительной и к -той преобразованной обмотками.

В приведённой матрице объединены преобразования для всех обмоток ЭД. Пусть задана матрица прямого преобразования числа фаз Пw, тогда можно записать и матрицу обратного ~ преобразования числа фаз Пwk j:

Π _w

cos( 9 W 1,1 )	cos( 9 w i,2 )	K	COS( 9 w i, m )
COS( 9 w 2Д)	cos( 9 w 2,1 )	K	cos( 9 w 2, m )
K	K
cos( 9 wn д)	COS( 9 wn ,2 )		cos(9 wn , m )

Эти матрицы, как правило, не квадратные, так как квадратными они могут быть лишь в одном случае – если исходное число фаз равно новому, что лишает преобразование смысла.

Матрицы П и Π не зависят от времени, так как входящие в них под знаком косинуса w углы постоянны и определяются только числами фаз. Прямое преобразование фаз:

uw (t) = п w . u( t), iw (t) = n w . i( t), vw (t) = Пw • Y(t), Х|/ц.w (9r) = П w • V^ (9r);

обратное преобразование фаз:

u ( t) = ⁿ w . u w ( t), i ( t) = ⁿ w . i w ( t),

_V( t ) = n w . V w ( t ),    (9 r ) = n w .у_ц w (9 r ).

~

В исходную математическую модель подставляется i(t) = п w • iw(t), обе части уравнения умножаются на матрицу прямого преобразования фаз Пw, учитывается, что п   d у( t) = dn w -у (t) = d^w (t)

^П w • u ⁽ t ) = u w ⁽ t ),

w dt dt         dt и уравнение электрического равновесия с новым числом фаз принимает вид d^^t) = -П w . R -П w . i w (t) + u w (t).

dt

Аналогично трансформируется выражение потокосцеплений через токи:

vw(t) = nw .L(6r)-Пw .iw(t) + Vwц(6r), откуда выражение токов через потокосцепления iw (t) = [П w - L(0 r )-flw ]-1 •[Vw (t) - Vw ц (0 r )].

Электромагнитный момент:

■=■■”* .:r: * *

+ iK-;-'"':""*

Одним из важнейших преобразований является преобразование системы координат, которое позволяет избавиться от тригонометрических зависимостей индуктивностей от угла поворота и даёт возможность некоторых дальнейших важных преобразований (линеаризацию, получение передаточных функций и др.). Общий ход преобразования системы координат напоминает преобразование числа фаз, т. е. также вводятся матрицы прямого преобразования П (от исходной раздельной системы к новой единой системе координат обмоток) и обратного преобразования П. Особенностью обеих матриц преобразования координат служит то, что их произведение даёт единичную матрицу, а также их зависимость от времени.

Переменные в новой единой системе координат обмоток (индекс s) через переменные в исходной системе координат (переменные без индексов): u,(О - П[.,(t)]■ u(t). i,(t) -П[.,(t)]■ i(t); ~- r         -I                                   ~- r         -I v5(t) = П[05 (t)] • Y(t), v^.5 (t) = П[05 (t)]• Yu(t), где 9n — угол поворота единой системы коорди-н т.

Переменные в исходной раздельной системе координат через переменные в новой системе координат: u( t ) = П [ 0 , ( t ) ] • u , ( t ), i( t ) =n [ 0 , ( t ) ] • i , ( t ); _V( t ) = n [ 0 , ( t ) ] • ^ ( t ), v ц ⁽ t ) = ^{n [} e s ⁽ t )] -\|/_u. s ⁽ t ), которые подставляются ^в исходную ^{математическ}ую модель ^и после соответствующих преобразований получают уравнение электрического равновесия:

db^H = - п - 1 [ е s ( t ) ] . r x,e s ( t ) ] . i s ( t )-n - i [ e s ( t ) ] .

• - d n^S s ) ■» s ( t )^ s ( t ) + u s ( t ).

de s где ωS – угловая скорость единой системы координат.

Уравнение потокосцеплений:

v S ( t ) = ^{n- 1} . L i s ( t ) + У_Ц. s ( t ).

Электромагнитный момент:

M =1 •

dV s (9 r )

59 r

• i s ( t ).

Полученные выражения конкретизируются для выбора системы координат обмоток путём выбора угловой скорости системы координат и _s . Наиболее характерными являются варианты её равенства нулю, угловой скорости ротора, частоте питания одной из обмоток. Главное, чтобы уравнения максимально упростились. В частности, для синхронных ЭД (в том числе с постоянными магнитами) скорость системы координат выбирают равной скорости ротора; для двигателя двойного питания — угловой частоте питания одной из обмоток. В результате уравнения освобождаются от периодических коэффициентов (зависимостей индуктивностей от угла поворота). Это существенно ускоряет моделирование и упрощает переход к алгебраическим уравнениям установившегося режима.

Ещё одним важным видом преобразования выступает учёт схемы соединения обмоток и подключения их к источнику питания. Можно выделить следующие схемы соединения обмоток: «раздельное подключение»; «звезда с общим проводом»; «звезда без общего провода»; «треугольник» («многоугольник»). У ЭД двойного питания возможны разные схемы соединения обеих обмоток и подключения их к источнику питания, представляющие собой комбинации перечисленных выше. Исходными являются уравнения, записанные для случая раздельного подключения, а для получения других схем соединения используют специальные матрицы преобразования. При этих преобразованиях целесообразно перейти от напряжений к рассмотрению потенциалов на клеммах обмоток. Например, для преобразования к схеме соединения обмоток «звезда без общего провода» используется матрица преобразования

1 -1 -1 K -1 1 о о о 0 1 о о о о 1 о 0 о о о 1 с помощью которой преобразуются токи i = ПmY • iY, подставляемые в уравнение равновесия напряжений (индексом Y обозначены переменные в схеме «звезда без общего провода»):

dd^ --R•ПmY • iY + (Ф-Фо), где Фо =

φ 0.1 φ 0.2

вектор потенциалов на нулевых клеммах обмоток; =

φ ₁ φ ₂

- вектор потен

Ф о. n

φn циалов на вторых клеммах обмоток; при этом u = ф - фо.

Уравнение потокосцеплений:

у = L •П_{m Y} • i _Y +\|/ _ц .

Матричное уравнение электрического равновесия необходимо умножить (слева) на матрицу Π SY преобразования системы уравнений:

^П SY

=п mY=

1	-1	0	0		0
1	0	-1	0		0
1	0	0	-1		0
		K	K		K
1	0	0	0	K	-1

в результате чего получается новое уравнение электрического равновесия:

d^Y = (-n sY • R -П m Y ) • i y +П sy • (ф - фо) . dt

Уравнение потокосцеплений:

V Y = ⁽ⁿ sy • L^m Y )• i y +ⁿ sy^ -

Электромагнитный момент:

M =2 i ^{Y (} t )-

= L YM 1 \ ( t )+L

66 r J 2

VsYfOr)

59 r

' i Y ⁽ t ),

где в новой схеме соединения обмоток матрица индуктивностей

L

Y =ⁿ SY • L -H m Y , потокосцепления от постоянных магнитов с обмотками:

V цY =ⁿ SY ^- VuY .

Аналогично выполняются преобразования модели для других схем соединения обмоток и подключения их к источнику питания. Отдельной задачей является сочетание различных схем соединения обмоток у ЭД двойного питания, что учитывается на этапе формирования матриц преобразования из отдельных подматриц, записанных для каждой обмотки по отдельности.

Следующий важный этап – переход к уравнениям для установившегося режима, выполняемый в процессе линеаризации модели. Для этого должна использоваться модель, которая получается после этапа преобразования координат и выбора конкретного значения её угловой скорости. При этом используется разложение в ряд Тейлора в окрестностях точки установившегося режима. Уравнения в приращениях удобно использовать для первоначального синтеза законов управления с последующим уточнением по исходным нелинейным моделям.

Линеаризация математической модели ЭМУ, например, в программе MathCAD выполняется следующим образом.

Все переменные записываются в виде двух составляющих – постоянной величины и приращения:

• -    переменные состояния уравнений электрического равновесия:

у ( t ) = _V( t 0 ) + A_V ( t ) = Vo +УД - 1 ;

i( t) = i( to) + Ai( t) = io + iA-t;

*'(*) ■*-(*o)'

....................

• -    переменные уравнения механического равновесия:

• 6 r (« =6' (t     : r . 6'0   'A" (

® r ⁽ t ) » r ⁽ t 0 > + ^Дт r ⁽ t ) » r ⁰ +™ r ^Д - t ^;

M st ( t ) = M st ( 1 0 ) + AM st ( t ) = M st 0 + M st A - 1 ;J

• - переменные в модели источника питания:

0( t ) = 0( 1 0 ) + A0( t ) = 0 0 + 0 A - 1 ; l

r

®(t) = Ю(t0) ■ \M( t) = Ю0 +®A- t J где индексом «0» обозначены значения переменных в точке линеаризации 10 (постоянные величины), а индексом Δ – малые приращения этих же переменных (зависящие от времени).

Затем используется символьный процессор с соответствующими командами символьных преобразований (разложение в ряд Тейлора). Для получения уравнений установившегося режима затем достаточно приравнять нулю переменную t , и из уравнений исчезают все приращения. Затем получают уравнения для приращений, вычитая из общих выражений линеаризованных уравнений установившиеся значения.

В результате получают две системы уравнений - алгебраическую для нахождения установившихся значений и дифференциальную в приращениях для отражения динамики. Первую систему уравнений решают, и ход решения различен для разных двигателей, т. е. формализуется для конкретных типов двигателей. Вторая система ввиду линейности может быть записана в общем матричном виде:

• -xL- = A - x ⁽ t >+ B - u ⁽ t >+G.⁽ t > _; 1 y( t ) = C . x( t ) + D - u( t ) + ^{H -} r⁽ t ) ,J

где векторы x - переменные состояния в данной разновидности модели (токи или потокосцепления); u – управляющие воздействия (амплитуды, частоты и фазовые сдвиги питающих напряжений); r - внешние воздействия (главным образом, момент нагрузки); у - вектор выхода (интересующие исследователя переменные состояния и некоторые другие переменные, рассчитываемые через переменные состояния, в частности, электромагнитный момент и др.); A , B , C , D , G , H - соответствующие матрицы, вид которых определяется типом ЭД и автоматизированно получается с использованием выше рассмотренных преобразований из исходных уравнений математического описания конкретного ЭД.

Из полученных уравнений имеем передаточные функции после преобразования по Лапласу:

• У ⁽ Р ) = [ Р E ^- A ] ^{- 1} • [ B • ^{u (} P )^{+ G} • ^{r (} P )] • ^{x (} P )^{+ D} • ^{u (} P )^{+ H} • ^{r (} P ) -

• Это выражение содержит матричную передаточную функцию, включающую частные передаточные функции для всех возможных сочетаний входных и выходных переменных. Выра-
• жения для передаточных функций возникают автоматически в виде полиномов с символьными коэффициентами:

W k ( p ) =

q ⁽ p ) h ⁽ p )

m

£ q ^- p¹

i =0 __________

n

£ hp¹

= 0

где m – порядок полинома числителя, n – порядок полинома знаменателя; k – номер переменной в соответствующем векторе выходных величин (состояния или выхода); j – номер переменной в соответствующем векторе входных величин (управления или возмущения).

Поскольку размерность числителей и знаменателей обычно более 2, аналитические исследования таких передаточных функций затруднены (их выполняют путём специальных упрощений с учётом соотношения полученных параметров передаточных функций). Наиболее доступными являются численные расчёты, включая определение полюсов и нулей, выделение на их основе типовых динамических звеньев, расчёт частотных характеристик. В эти выражения входят установившиеся значения переменных в точке линеаризации, которые берутся из решения соответствующих алгебраических уравнений для установившихся режимов. Передаточные функции можно использовать при проектировании замкнутых и разомкнутых систем ЭМС с использованием известных принципов их построения.

Полученный комплекс содержит модели, которые обладают различной степенью детализации и идеализации. Например, при получении исходной модели можно использовать самое общее представление о функциональных зависимостях индуктивностей (и потокосцеплений от постоянных магнитов) от угла поворота ротора (например – имеются ли вообще такие зависимости). Но в то же время можно получить экспериментальные характеристики для этих зависимостей, которые будут очень точно отражать все неидеальности этих зависимостей [7]. Поэтому такая модель может использоваться и для концептуального проектирования (на самом общем уровне), и на поэлементном (на самом детальном уровне). Как правило, для каждого последующего преобразования вводятся свои допущения, среди которых можно выделить электрическую симметрию (равенство параметров фаз одной и той же обмотки), геометрическую симметрию (равномерное распределение обмоток) и косинусоидальную зависимость индуктивностей от угла поворота ротора.

Моделирование процессов ЭМС в специальных режимах

В процессе работы ЭД возможно подключение и отключение его обмоток, что связано как с нормальной работой транзисторно-диодных ключей, так и с аварийными режимами обрыва фаз, перегорания транзисторов и т. п. Знать особенности таких режимов следует для разработки алгоритмов управления транзисторными коммутаторами и для диагностики неисправностей (например, для их предотвращения).

Произвольное подключение и отключение фазных обмоток приводит к преобразованию структуры схемы замещения с изменением замкнутых контуров протекания токов, числа переменных состояния и выходных переменных. Другими словами, ЭД в этих режимах описывается моделью с переменной структурой в виде комплекса взаимосвязанных частных моделей,

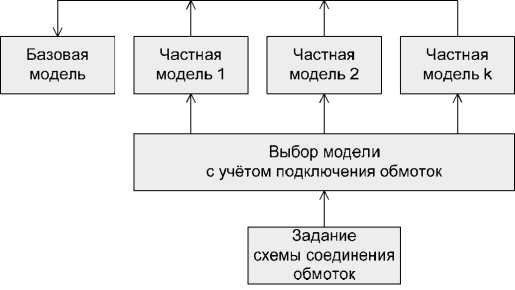
Рис. 2. Обобщённый алгоритм работы системы моделирования с учётом подключения и отключения фазных обмоток которые последовательно сменяют друг друга в процессе работы ЭД. При смене модели необходимо обеспечить, чтобы конечные значения переменных состояния, полученные при интегрировании предыдущей модели, были начальными для интегрирования следующей модели. Применительно к ЭД переменными состояниями, сохраняющими свои значения при изменении структуры, являются потокосцепления. Эти потокосцепления возникают как в замкнутых обмотках, так и в разомкнутых, и в них по закону электромагнитной индукции всегда наводится ЭДС: но в замкнутых контурах, кроме того, протекает ток, а в разомкнутых – не протекает.

Таким образом, в качестве переменных состояния для модели ЭД с переменной структурой выбираются потокосцепления.

В качестве выходных переменных необходимо выбрать такие, которые связывают ЭД с другими устройствами. Это электромагнитный момент (поступающий в модель механической нагрузки), а также фазные токи и потенциалы на клеммах отключённых фаз (поступающие в модель транзисторного коммутатора). Токи используются при определении путей их протекания (через транзистор или обратный диод), а потенциалы на клеммах – для использования при новом подключении фазы. Потенциалы источника питания (выхода транзисторного коммутатора) и фазы в этом случае оказываются разными, что вызывает протекание того или иного тока через источник питания.

Методика получения универсальной математической модели двигателя для режимов работы с различным числом подключённых фаз заключается в следующем. Разрабатываются базовая и частные математические модели, которые действуют во взаимосвязи (рис. 2).

Частные математические модели полностью отражают специфику подключения фаз и наличие тех или иных контуров. В них рассчитывают для всех фаз (подключённых и отключённых) активные проводимости, токи и их производные, потокосцепления и их производные, а также потенциалы на клеммах отключённых фаз. Эти результаты передают в базовую модель. Базовая математическая модель сама по себе не отражает специфики подключения фаз в данный момент. Она записана в самом общем виде с потокосцеплениями в качестве переменных состояния, и с её помощью рассчитывают производные потокосцеплений для всех фаз (в том – 201 – числе отключённых). Задача базовой модели – устанавливать связь между частными моделями, которые отличаются составом переменных состояния. Программа численного интегрирования работает с обобщённым вектором переменных состояния из базовой модели и «не замечает» различий в модели двигателя при смене её структуры, так как переменные состояния для неё всегда одни и те же.

Так как возможно отключение различного числа фаз в различных сочетаниях, необходимо рассмотреть все возможные варианты. Например, для трёхфазного индукторного двигателя двойного питания возможны варианты: 1) подключены все фазы; 2) подключена какая-то одна фаза - a, b или c ; 3) подключены по две фазы в разных сочетаниях - а и b, а и c, b и c ; 4) отключены все три фазы. Эти варианты справедливы для обеих многофазных обмоток ЭД, поэтому общее число возможных структур модели составляет 8×8=64.

Для многофазных ЭД число вариантов структуры ещё более возрастает, поэтому такие модели получают автоматизированным образом с помощью символьных процессоров, как это рассмотрено выше.

Одним и важнейших этапов автоматизированного проектирования ЭМС является моделирование динамических процессов. Если ЭМС рассматриваются как возможный вариант прецизионного ЭП, например, системы поворота антенны КА, то погрешность отработки составляет доли градуса, что требует применения математических моделей, обеспечивающих расчёты с такими погрешностями. Это возможно, в частности, при использовании моделей с таблично заданными параметрами ЭД, полученными экспериментально при параметрической идентификации [7], при учёте реальной формы питающих напряжений и других факторов. Но такая модель оказывается очень сложной, особенно если система управления ЭМС замкнутая и включает сложную нагрузку, прецизионные датчики и т. д. Всё это приводит к тому, что время моделирования становится неприемлемо большим, например, один прогон занимает несколько часов. Использование более простых моделей обеспечивает быстрое моделирование (минуты), но даёт результаты с неприемлемо большой погрешностью. Таким образом, при моделировании прецизионных систем возникает противоречие между точностью и скоростью вычислений. В НУЛ САПР СФУ развивается оригинальный подход, заключающийся в создании адаптивной системы моделирования. Современные системы моделирования уже являются частично адаптивными: они позволяют использовать разные методы расчётов (в том числе менять их в процессе счёта), подбирать шаг интегрирования и т. д., но в данном случае предлагается также менять используемые модели (рис. 3).

Модель 1

Модель 2

Ист очник пита ния

Вход 1          Модель 4

Выход 1

Двигатель

Модель 3

Модель 1

Модель 1

Модель 2

_______к Нагрузка

Вход 3 2     | Модель 4~|

Выход 3

Блок выбора моделей

Рис. 3. Принцип динамической смены моделей в системе моделирования

Каждый элемент ЭМС (например, Источник питания, Двигатель, Нагрузка) имеет по несколько моделей разной степени детализации. В процессе моделирования возможна замена моделей с тем, чтобы при пониженных требованиях к точности (например, при разгоне ЭД) использовали более простые модели, а в случае повышенных требований к точности (например, при подходе к заданному углу позиционирования) переключаться на более точную (и более сложную) модель. В этом случае можно обеспечить точность (в отдельных режимах, где это нужно) и приемлемую скорость вычислений (в целом). Основная проблема связана с тем, чтобы обеспечить автоматическую и корректную смену моделей по некоторым алгоритмам.

Заключение

Создание АРМ электромеханика, обеспечивающего автоматизированную разработку математических моделей изготовленных элементов, их параметрическую идентификацию, синтез законов управления и их отработку на готовом макете ЭМС, позволяет повысить надёжность проектирования, под которой можно понимать вероятность успешной реализации спроектированной ЭМС и обеспечения ею требований технического задания. Адаптивная система моделирования дает возможность выполнять расчёты процессов в прецизионных ЭМС с высокой точностью за приемлемое время.

Данная методология и реализующая её технология проектирования разрабатываются и совершенствуются в НУЛ САПР СФУ, передаются в ОАО ИСС и начинают использоваться в настоящее время для разработки перспективных ЭМС для КА различного назначения.