Электрон-электронные взаимодействия в умеренно легированном гетеропереходе AlxGa1-XaS/ GaAs

Электрон-электронные («e-e») взаимодействия играют определяющую роль в кинетических явлениях, среди которых следует отметить эффекты горячих электронов, квантовые поправки к проводимости и затухание (разрушение) квантования Ландау в объёмных и двумерных полупроводниковых соединениях с вырожденными электронами [1]. Для корректной теоретической интерпретации экспериментов необходимо нахождение явного вида зависимостей времени элек-трон-электронных взаимодействий от температуры T _ee ( T ) в приближении хаотических фаз [2].

Суть метода состоит в следующем. Роль внешнего возмущения играет потенциал экранирования, в который входит диэлектрическая функция электронного газа. Далее, фурье-образ внешнего возмущения (обычно ограничиваются вторым членом разложения) подставляется в уравнение Больцмана, результатом решения которого является время «e-e» релаксации. Решение этого интегро-дифференциального уравнения представляет большие математические сложности. В первую очередь это связано с необходимостью точного учёта потенциального профиля квантовой ямы. Чаще всего (см. например, [3]) используется в качестве аппроксимации бесконечная прямоугольная квантовая яма, что делает все последующие преобразования неприменимыми для исследования более сложных квантовых структур.

Зонные диаграммы исследованных наноструктур были рассчитаны методом самосогласованного решения уравнений Шредингера:

— ... d + E (z)] ^з (z)= Ej ^з (z)(1)

с граничными условиями ф3 (0) = 0, ^j (те) = 0(2)

и Пуассона d 2 V   4np(z)

E (z) = —eV (z), — dZ2 = ~X"

с граничными условиями

V (z = те) = 0, eV(z = 0) = E0,(4)

где χ — диэлектрическая функция.

Самосогласованное решение системы (1)–(4) представляет определённые трудности из-за неопределённости распределения плотности заряда p ( z ).

В ряде работ [4] уже были предприняты попытки расчёта зонных структур гетеропереходов, однако авторы ограничились численным методом и не получили аналитического решения. Кроме того, в решении системы (1)–(4) могут возникнуть разного рода расходимости, существенно влияющие на конечный результат.

Поскольку суммарный интеграл

Q =

∞

j p ( z ) dz = 0 ,

то в первом приближении должны существовать две области положительного и отрицательного зарядов: z < D и z > D с условием p ( z = D ) = 0. Поскольку p ( z = 0) = eN 3 / ² ( N о — уровень легирования), то простейшая аппроксимация такова:

/ p ^{( z} ) = eN 0³ / ² (1 ^- -§) , ^z< D, ( p ( z ) = —A exp( — ( z — D ) /a ) , z>D.

Подставляя систему (6) в (5) и интегрируя, полу-

чим

A =

eN 03 / ² D

2 a

Далее, подставив (6) в (3), после простых преобразований получим распределение потенциала:

V ( z ) = — 2 n[e„ 3 / ² ( z ² — z L)] ₊

4 neN 3 / ²   1 ₉   1    \                 . .

--°^ 3DD ^{2 +} 2 Da) , ^{z   (7)}

. .     2 neN3/ ² D        . .        . , .

V ( z ) = -----⁰---- a exp ( — ( z — D ) /a )

z>D.

Моделирование потенциала имеет существенный

недостаток: произвол в определении постоянных a и D . Кроме того, используя данный метод, не

удаётся решить уравнение Шредингера (1). В какой-то мере произвол можно снять с помощью граничного условия (4):

E (0) = —eV ( z = 0) = -

4 ne ² N °/ ² ( 3 D ² + 2 aD )

χ

.

Откуда следует связь:

a =

XE ⁽⁰⁾  +2 D

2 ne ² N 3 / ² D   ³

Для решения уравнения (1) преобразуем его к виду

/    1 d ²      V ( z )A , . .

EF ( ^— k F 42 ⁺ " E T) * ^{( z} ) = ^E - * j ^{( z} > ■

Из уравнения (11) получим

8 nm * e ² k F X №   n ^{( z )} =

∞

= -°- ( в + 1) a ² £( — 1) n e n ( n +1) ² x E

^F          n =0

x exp (—(n + 1) Az), а затем будем варьировать E(z) в известных пределах и построим параметрическую зависимость функции E(z) от A (рис. 1). На этом же рис. 1 изображено решение системы (7)–(8). Подгоночными параметрами были выбраны λ и β. Анализ показал, что зависимость v(в) достаточно слабая.

E(z), мэВ

где E F — уровень Ферми, связанный с волновым вектором k F соотношением

E F =

fi ² k F

2 m *

Для 2D-электронного газа справедливо k F = V2 nn s , где n s — концентрация 2D-элек-тронов.

Систему уравнений (1)–(4) удобно решать в новых безразмерных переменных:

V ( z )       ( \ ^ез г           U

• -5— = V ^{( z} ) ■ TT" = E j ■ ^z = ^zk F ■ E F         E F

• p ( z ) = —en ( z ) k F ■ ^ ( z ) = ^ >( z ) k F/ ² .

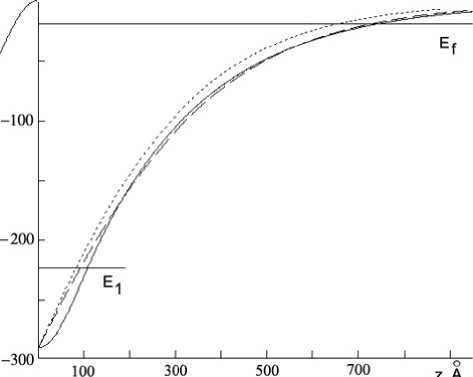
Рис. 1. Профиль потенциальной ямы: сплошная — решение системы (7)–(8); пунктирная — зависимость (13) при А = 0 , 5 • 10 6 , в = 0 , 7; штриховая — зависимость (13) при А = 0 , 45 • 10 6 , в = 0 , 7

Исходная система в новых переменных запишется

как

d ²

( ^— — ⁺ V ^{( z )} ) ^ j ^{( z )} = E j ^ j ^{( z} ) ■

d 2 ϕ dz ²

8 nm * e ² k F

X fi    n ^{( z )} ■

Решение уравнения (10) представим как

^ k ( z )= C ( k ) sin [ kz + n ( k )] ■        (14)

с граничными условиями

V ( z = ^ ) = 0 ■

( — dV ) , =° = ^P F I n ( z )^  (12)

^ j (0) = 0 ■ ^ j ( z = ^ ) = 0 .

В отсутствии внешних полей интеграл в (12) равен нулю.

Будем искать решение уравнения (11) в виде

где C ( k ) будет определяться из условий нормировки:

L

C 2 ( k ) J ^ 2 ( z ) dz = 1 .             (15)

Представляя (14) в виде

∞

^ + ( z ) = exp ( ikz + in ( k )) У^ b j ( k ) exp ( — jAz )

j =0

и подставляя в уравнение Шредингера (10), получим

∞

V ( z ) = c £ ( — 1) ^п в n exp( — ( n + 1) Az ) ,    (13)

n =0

где β, λ — некоторые подлежащие определению константы, а c определяется из граничных условий как

V 0

c   E f E I =0 ( — 1) n e n

= V ⁰ ( в + 1) .

E F

—k ² £ b j ( k ) — 2 ikA £ b j ( k ) j + A ² £ b j ( k ) j ² + j =0              j =0             j =0

+ [ EV 0 ( в + 1) £2 ( — 1) n e n exp( — ( n +1) Az ) — E^ x

∞ x £ bj(k)

j =0

exp ( —jAz ) = 0 ,

b1(k) = - EfA (A2 + 4k2) (A + 2ik), bj(k) = -EfA(j3A2+4k2j) [jA + 2ik1 X

X £ ( - 1) n e n b j- ( n +1) , n =0

где b о = 1, которое определяется из условия нормировки (15).

Фазовый сдвиг определяется суммой

52 bj(k) = - exp(-in(k))• j=0

На рис. 2 показана зависимость E(z), квадрат модуля волновых функций электронов на энергетическом уровне основной E1 подзоны размерного квантования. Для решения поставленной задачи реальный профиль E (z) зоны проводимости гетероперехода аппроксимируем треугольной ямой, так как это представлено на рис. 2. Рассмотрим двумерный электронный газ, находящийся в треугольной потенциальной яме. Представляя в области 0 < z < d потенциальный профиль в сферической системе координат как г       Eо - E1   г

E ext ( r ) =--- d---r - E 0

с граничными условиями

E 0 = E ext (0) , E 1 = E ext ( d ) •

Фурье-образ кулоновской экранировки будет иметь вид

1     d ² r

Vext (q) = S   (2П)2 eXP (-iqr) Eext (r), где S = L2, L — линейные размеры системы, а фурье-образ полной экранировки:

V tot ( q," ) =

V ext ( q ) e ( q," ) ’

где диэлектрическая функция в приближении хаотических фаз (ПХФ) имеет вид

= 1 - ^{2 n}e ² f d ² k ^f k-q/ 2 ^{- f} k + q/ 2

⁽ q, )         q J (2 n ) ² A ² kq/m * + Пш '

В соответствии с теорией возмущений

± = [ d" £,£,№ (Q," )|2 6 (Ek (k + q) + i -∞ j,k,l k,p,q

+ E l ( p - q ) - E i ( k ) - E i ( p )) X

Xf k f p (1 - f k + q )(1 - f p-q ) ,        (16)

где V ijk¹ ( q," ) — матричный элемент полного потенциала экранирования, а f — функция Ферми-Дирака. В случае одной заполненной подзоны имеем i = j = k = l = 1. Здесь отступим от

ТРУДЫ МФТИ. — 2010. — Том 2, № 1(5) традиционного (численного) метода решения задачи, использовав нормировку вероятности элек-трон-электронных переходов на δ -функцию. В результате в процессе интегрирования (16) встречаются лишь сингулярные члены. Это позволило проинтегрировать (16) в элементарных функциях и получить результат, удобный для анализа. Воспользовавшись в процессе вычисления тождественным преобразованием

£ f k (1 - f k + q ) 6 (A " - E k + q + E k ) = k

= П (exp (-vAШ) + 1)3 [X0 (q,")]’ где fk - fk+q               1

X о ⁽ q," ^{:  2}> "E---- p ---^-^x , v = T^^

ПШ - E k + q + E k + iO      k B T

E(z), мэВ

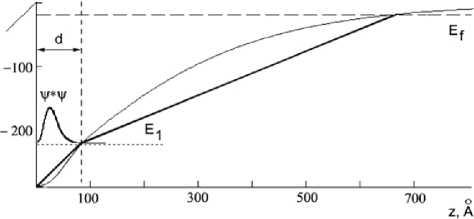
Рис. 2. Фрагмент E (z) гетероперехода при ns = 6,3 • 101 см~ . Показана аппроксимация реального распределения потенциала треугольным профилем с изломом в точке пересечения с уровнем E1

Приходим к окончательному выражению:

/ 1 Y ⁿ"“    ( E 0 - E 1 ) 2П v, , , .   , , . , .

(. -J     = m * E F dn 2 ^[ * ^{1 (} v ⁾⁺ * 2 ⁽ v ⁾⁺ * ^{3 (} v ^)l+

V ⁸ m * E F                ^e L ^{e 2} L ² m *  va x

⁺ n 2 E F m * d 2 ^{( E 0 - E} 1) [^{( E 0 - E} 1) "- Л П 2- ^{- V 0} d ^X

X [ * 1 ( v ) + * 2 ( v )| +

E 0                     e ² L ² m ^∗

+ П3AvEFd [E0d - (E0 - E 1) -ПЛ?-J *3 (v), где vEF                vEF

1       5 (2 B - vE F ) ²           5 (2 B - vE F ) ² ,

* 2 ⁽ v ) = 6(2 Bv - vE F ) ['“⁽ B ) ^- 6 ■ (2 B^E F vE F ) ' •

, , )        ( vE F ) ⁶     _l / vE F A ,     ( vE F ) ⁵

• ³      5(2 B - vE _F ) ^{7 П} \2 b) (2 B - vE _F ) ⁶

_     ( vE f ) 4     +    ( vE f ) 3 ___ ( vE f ) 2

2(2B - vEF)5 (2B - vEF)4 2(2B - vEF)3 • Проанализируем последнее выражение. По смыслу входящих в него величин можно указать, что основными факторами, влияющими на интенсивность электрон-электронного взаимодействия, являются температура и параметры потенциальной ямы. Оценим вклад каждого из них. Преобразуем (17) к виду

Ctra = ai (Eо,Ei,d) pi (v) +

+ a 2 ( E о ,E i ,d ) p 2 ( v )+ p з ( v ) , (18) где функции σ n зависят только от параметров ямы и являются безразмерными, а p n — от температуры и имеют размерность времени. Вышеуказанные функции представлены на рис. 3 и 4, а зависимость времени релаксации от температуры на рис. 5.

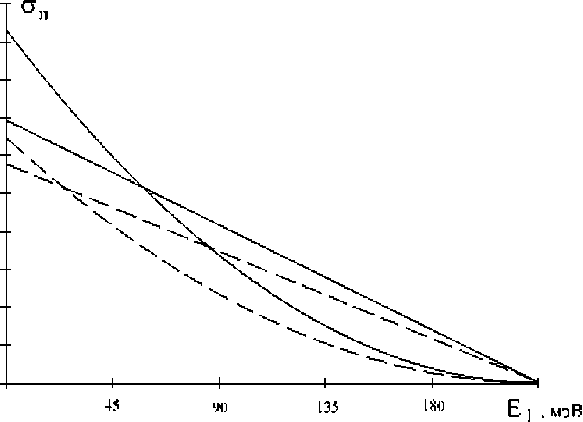
Рис. 3. Характер воздействия на σ n суммы (9) параметров E 1 и d для реальных гетероструктур при E 0 = 225 мэВ. Сплошные кривые — σ 1 , σ 2 при d =86 ^˚A, штриховые кривые — σ 1 , σ 2 при d = 100 ^˚A

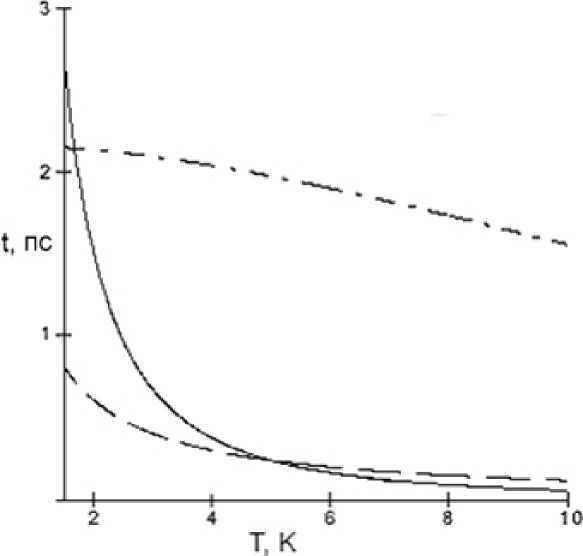
Рис. 4. Вариационный вклад в температурную зависимость компонентов p n в (9) при E 0 = 225 мэВ, E 1 = 165 мэВ, d =86 ^˚A. p 1 — сплошная кривая, p 2 — штриховая, p 3 — штрихпунктирная

Сравним выражение (18) с экспериментальными данными [4] (рис. 5). Варьируя параметры ямы в известных пределах, возможно добиться удовлетворительного согласия с результатами работы [3]. Как видно из рис. 2, имеются три параметра, задающих треугольную яму. Зафиксируем один из них (пусть это будет E0 ) и будем варьировать два других (ширина ямы d и E1). Из рис. 2 следует, что влияние первых двух слагаемых в (18) при значениях E1 > 135 мэВ будет несущественным и ход температурной зависимости времени «e-e» взаимодействия полностью определяется третьим слагаемым — p3 (v), повторяющим экспериментальные кривые.

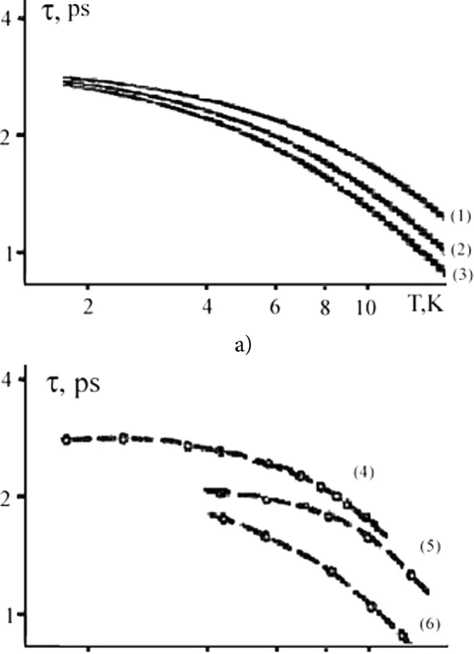
2 4 6 X 10 Т.К б)

Рис. 5. Сопоставление теоретических (а) и экспериментальных (б) зависимостей для n s =8 · 10 ¹¹ см ^{- 2} —(1)и (4), n s =6 , 9 · 10 ¹¹ см ^{- 2} — (2) и (5), n s =6 , 3 · 10 ¹¹ см ^{- 2} — (3) и (6)

Таким образом, аппроксимируя реальный профиль гетероперехода треугольной ямой, когда под уровнем Ферми имеется лишь одна заполненная подзона размерного квантования, удаётся добиться хорошего согласия результатов расчёта τ ee — времени внутриподзонной релаксации с экспериментальной зависимостью. Подгоночными параметрами служила лишь характеристика потенциальной ямы наноструктуры.