Электронный образовательный контент, предназначенный для формирования профессиональных компетенций бакалавров направления подготовки "Прикладная математика и информатика"

Переход на цифровые методы управления, передачи и обработки информации приводит к необходимости внедрения новых образовательных программ [1-3] и соответствующих им методологических подходов. Опыт работы Нижегородского государственного университета им. Н.И. Лобачевского в проектах МЕТАМАТН и TUNING RUSSIA [1-3, 5-6] дал возможность университету разработать собственный образовательный стандарт для информационно-коммуникационных технологий [7,8].

Реализация образовательных программ современных образовательных стандартов невозможна без применения технологий, использующих электронные образовательные средства [9-12]. Формирование профессиональных компетенций, в основном, происходит при изучении специальных дисциплин, в большинстве которых рассматриваются методы построения и исследования математических моделей [1320], а также при прохождении учебной, производственной практик и выполнении выпускных квалификационных работ. На этих стадиях обучения фактически основной (творческой) проблемой является создание адекватных математических моделей. Огромный класс процессов в природе, в частности, в технике являются периодическими. Для них представляется необычайно важным исследование вопроса устойчивости колебаний и возбуждения автоколебаний, например, в машиностроении [17,20], в энергетике [19] и др.

Для формирования навыков, необходимых для построения математических моделей колебательных систем в Институте информационных технологий, математики и механики Нижегородского государственного университета им. Н.И. Лобачевского разработан программный комплекс, написанный на языке программирования С++ в среде визуального программирования Borland C++Builder ^ТМ . Программный комплекс позволяет находить наиболее значимые причины самовозбуждения колебаний путем анализа геометрической схемы связей изучаемой динамической системы. В работе описываются физические подходы и методика поиска наиболее значимых причин самовозбуждения колебаний механических систем, основанная на понятии геометрической схемы связей [21] и теории чувствительности [18,22-27].

1.    Решение задачи определения наиболее значимых причин самовозбуждения колебательных систем с большим числом степеней свободы 1.1.    Энергетический анализ причин самовозбуждения колебаний

При подготовке к работе с программным комплексом студенты имеют возможность ознакомиться с определенным классом многомерных колебательных систем, которые можно представить в виде некоторого числа взаимосвязанных осцилляторов [21]. Математическая модель, описывающая колебания таких систем, записывается следующим образом: n

^ ( mjq j + bjq j + cjqj ) = 0, i = 1,2..n.

Если фиксировать в рассматриваемой системе все координаты, положив их равными нулю кроме i -ой, то она выродится в систему с одной степенью свободы, описываемую линейным уравнением второго порядка вида

miiqi + biiqi + c^i =0, где параметры тц, b^ и Сц являются массой, коэффициентами собственного трения и собственной жесткости парциального осциллятора, отвечающего координате q .

Запишем i -е уравнение системы в виде miiqi + biiqi + c^i

- ^ i ⁽ mi jq J + bijq J + cijqj ) ^.

Это уравнение будем рассматривать как уравнение движения i -го осциллятора, под действием силы Fi , равной

Fi =- ^ i ⁽ mJj + ^bijq j + cijqj ).                   (4)

Эта сила Fi  есть суммарное воздействие на i -й осциллятор всех остальных осцилляторов. При этом j -й осциллятор действует на i -й с силой fij = - mijq j - bijq j - cijqj .                     (5)

Аналогично i -й осциллятор действует на j -й с силой fJi = -mjiqi -bjiqi - ^i.

Это взаимодействие двух осцилляторов будем разделять на взаимодействие по координате, скорости и ускорению, и кроме того, на взаимные и направленные согласно таблице 1.

Таблица 1.

Классификация связей

Силы взаимодействия (связи)	По координате	Скорости	Ускорению
Взаимные	ci J = cJi упругости	bU = bJi трения bi J = — bJ i гироскопические	mij = mji инерционные
Направленные от i -го осциллятора к j -му	ci J = °’ cJi * 0	bi J = °’ bJ i * °	mij = °’ mji * °

Взаимное координатное взаимодействие вместе с собственными силами жесткости имеет потенциальную функцию

12   12

2 ciiqi ⁺ cijqiqj ⁺ 2 cjjqj ■

Взаимные и собственные трения могут быть представлены так называемой диссипативной функцией

1     2                1      2

2 biqi + bijqi^ j + 2 bjjq j, а взаимные инерционные взаимодействия вместе с собственными инерционными силами – кинетической энергией

1       .2

■

- mii^i ^{+ m}ijqiqj

⁺ 2 mjjq j •

Пусть взаимодействия между осцилляторами разделены на взаимные и направленные. За коэффициентами взаимных сил сохранены старые обозначения, а коэффициенты направленных сил обозначены ту, bi^, с j. В соответствии с этим разделением запишем систему уравнений (1) в виде

Z ^{( m} j q j + ^т ijqj + bjjq j + byq j + ^Cijqj + Cyqj ) = 0 .              ⁽1⁰⁾

Умножим уравнения (10) на q j и просуммируем их. В результате после простых преобразований можно прийти к соотношению вида

d

• — ( T + П ) =- 2 F - A - B - C ,                      (11)

dt где T, F и П - так называемая кинетическая энергия, диссипативная функция и потенциальная энергия,

• ^2T = Т ^mj^qq j ,   ² F = Tbyqqqj ,   ² П = T ^Cijq_tqj , ⁽¹²⁾

а A , B и С – функции вида

A = S /~ jq qqj , B = S bjqqqj ,     C = X c_yq q .    (13)

Силы взаимодействия, не меняющие величину T + П , назовем консервативными, силы, всегда уменьшающие ее, – диссипативными и силы, могущие ее увеличивать, – активными. Из уравнения изменения энергии (11) непосредственно следует:

• а)    собственные и взаимные упругости и инерционности, а также гироскопические силы – консервативные;

• б)    собственные и взаимные трения, для которых соответствующая часть функции F положительна, – диссипативные, а для которых отрицательна – активные;

• в)    все направленные силы – активные.

Так как при самовозбуждении колебаний в системе ее энергия увеличивается, что может произойти лишь под влиянием активных сил, то для изучения самовозбуждения системы прежде всего следует проанализировать структуру и характер связей.

• 1.2.    Геометрическая схема связей и функции чувствительности

Для анализа роли связей введено в рассмотрение геометрическую схему связей ( ГСС ) [21]. Она представляет собой систему взаимодействующих между собой парциальных осцилляторов, которые обозначаются точками, а действующие между ними направленные и взаимные связи (силы) соответственно направленными и ненаправленными отрезками. Замкнутый контур без самопересечений, составленный из ненаправленных отрезков и по крайней мере одного направленного, проходимого в одном направлении, назовем циклом .

Согласно работе [21] основными механизмами возникновения неустойчивости в системах, допускающих осцилляторное представление, являются: а) нарушение так называемой статической устойчивости, когда функция П теряет положительную определенность и становится знакопеременной; б) появление отрицательной диссипации, т.е. возможности подкачки энергии в систему за счет так называемых отрицательных трений; в) наличие замкнутого цикла воздействий с направленной связью, могущей вкачивать энергию в систему.

Поскольку различные связи и циклы по-разному влияют на самовозбуждение колебаний в системе, то для выяснения наиболее опасных причин самовозбуждения была использована теория чувствительности.

Формирование теории чувствительности началось в конце 50-х годов прошлого века с работ Г. Боде [22] в связи с бурным развитием теории управления и теории электрических цепей. Дальнейшее развитие теории чувствительности шло по двум направлениям: первое было обусловлено решением задач автоматического регулирования, теории управления и технической кибернетики [22-26], второе – решением задач анализа и синтеза сложных колебательных механических систем [26,27].

Под функцией чувствительности понимается частная логарифмическая производная от показателя динамического качества Qi по одному из параметров системы а

j

Ф ( Qi , а j ) =

5 ln Qi д ln а j

дQi I Qi ^5aj / ^aj ’

i = 1,2,..., n ,

где Q_i - отражает работу направленных связей i -го цикла.

Понятие функции чувствительности может быть использовано для поиска наиболее значимых причин самовозбуждения колебаний в активных системах. Предложенная в работе методика поиска наиболее значимых причин самовозбуждения колебаний опирается на понятие геометрической схемы связей и цикла.

В дальнейшем напрямую функция чувствительности не используется, но студенты получают в рамках самостоятельной работы необходимую информацию о мощном аппарате теории чувствительности из предложенных преподавателем источников, что способствует повышению уровня освоения компетенций. В программном комплексе используется более простой и наглядный метод для исследования не слишком сложных линеаризованных динамических систем, описываемых системой дифференциальных уравнений

( M + M ) q ( t ) + ( В + B ) q ( t ) + ( C + C) q (. t ) = 0 ,                     (15)

где q (t) - вектор обобщенных координат; M, В, С - симметричные матрицы инерционных, диссипативных и жесткостных параметров; М, В, (2   - несимметричные матрицы, элементы которых характеризуют направленные связи (силы) по ускорению, скорости и координате.

Так как студенты во время работы с программным комплексом вводят элементы матриц, входящих в систему уравнений (15) в интерактивном режиме, то уже на стадии формирования матриц они имеют возможность выделить опасные связи и циклы. Более подробное исследование чувствительности циклов и направленных связей производится автоматически.

• 1.3.    Алгоритм и программный комплекс

На основе предложенной методики разработан алгоритм поиска наиболее значимых причин самовозбуждения колебаний, который включает в себя следующее:

• -    формирование матриц математической модели, описывающей самовозбуждение колебаний;

• -    построение геометрической схемы связей;

• -    расчет собственных частот и форм колебаний, нахождение потенциально неустойчивых форм колебаний;

• -    расчет функций чувствительности циклов и отрицательных трений;

• -    выделение чувствительных циклов и отрицательных трений с определением их вклада в процентном отношении в работу активных сил, увеличивающих полную энергию системы.

Интерфейс пользователя представлен в виде различного рода меню, диалоговых панелей и диалоговых окон, a также главного окна приложения.

Входными параметрами являются коэффициенты матриц, определяющие математическую модель, а также коэффициенты матриц, которые определяют геометрическую схему связей. В ходе ручного ввода матриц масс и жесткости программа автоматически контролирует симметричность коэффициентов матриц в соответствии с последним изменением. Симметричность коэффициентов матрицы диссипации проверяется с заданной точностью. Положительную определенность матриц пользователь может проверить, выбрав соответствующий пункт в меню «Проверка». В сеансе работы в главном окне приложения выдаются комментарии и подсказки о требуемых действиях.

На рисунке 1 представлено главное меню программного комплекса.

Матрицы взаймы* связей Матрицы мапраелевиых семей |

Матрица масс | Матрица диссипащ^ | Матрица жесткости |

систем 3

Показывает текущую-размерность системы^

Показывает число ■ циклов -на ГСС^

Рис. 1. Главное меню программного комплекса

Главное меню комплекса включает в себя следующие режимы: ─ «Файл»;

─ «Правка»;

─ «Проверка»;

─ «Вычисления»;

─ «Помощь».

В режиме «Файл» пользователю предоставляется возможность:

─  создать новую работу;

─  открыть ранее сохраненную работу;

─ сохранить текущую работу;

─ вывести результаты вычислений текущей работы на печать;

─ выйти из комплекса.

Режим «Правка» позволяет:

• -    изменять размерность системы;

• -    изменять точность численных методов и округления вывода на экран. Режим «Вычисления» позволяет:

• ─    вычислять собственные частоты и собственные формы колебаний; определять потенциально неустойчивую форму колебаний;

• ─    определять циклы на геометрической схеме связей;

• ─  вычислять чувствительность циклов;

• ─  вычислять работу отрицательных трений.

2. Пример использования программного комплекса

Результаты вычислений выдаются в виде таблиц в главном окне.

Режим «Помощь» позволяет просмотреть файл помощи с описанием программы и краткие сведения о программном комплексе.

В качестве примера работы комплекса рассматривается задача об исследовании причин самовозбуждения малых колебаний кузова и передней подвески автомобиля при равномерном прямолинейном движении с постоянной скоростью V . При построении математической модели [28] в качестве обобщенных координат выбираются поперечные ( y ) и угловые ( Θ ) перемещения кузова, угловые перемещения ψ и ϕ передней подвески относительно горизонтальной оси, направленной по движению, и, соответственно колес, относительно вертикальной оси. Численные значения параметров соответствуют автомобилю ПАЗ-3205.

Результаты численного эксперимента представлены на рисунках 2, 3 и 4. На рисунке 2 представлены результаты расчета собственных частот и форм колебаний.

вд                                           ООО

Файл Правка Проверка Вычисления Помощь

SMSZtoET"

Матрицы взимных связей ] Матрицы направленных связей Результаты расчетов |

Собственные частоты и формы

Порядковый номер	1	2	3	4
Собственные числа	15,253846	36,711155	45,268973	258,3151
Собственные частоты	2,427724 Гц	5,042762 Гц	7,204781 Гц	41,112125 Гц
V[1]	-0,000211	0	-0.066313	-0.000337
V[2]	0	1	0	0
V[3]	-0,999999	0	0,997783	0,004514
V[4]	1Е-6	0	0,005608	-0,99999
Г 1-ая форма потенциально устойчивая Г 2-ая форма потенциально устойчивая -> 3-ая форма потенциально неустойчивая Г 4-ая форма потенциально устойчивая

’азмерность системы 4

Рис. 2. Результаты расчета собственных частот и форм колебаний

В программном комплексе автоматически формируется геометрическая схема связей по созданным матрицам масс, диссипации, жесткости, взаимных и направленных связей. На рисунках 3 и 4 представлены циклы, на которых осцилляторы Θ, y,ψ и ϕ обозначены соответственно цифрами 1, 2, 3 и 4, а направленные и взаимные связи по координате, скорости и ускорению – сплошной, пунктирной и штрихпунктирной линиями со стрелкой и без стрелки соответственно. Циклы неравнозначны между собой. Используя функции чувствительности найден процентный вклад каждого цикла в суммарную работу всех циклов на потенциально неустойчивой форме колебаний.

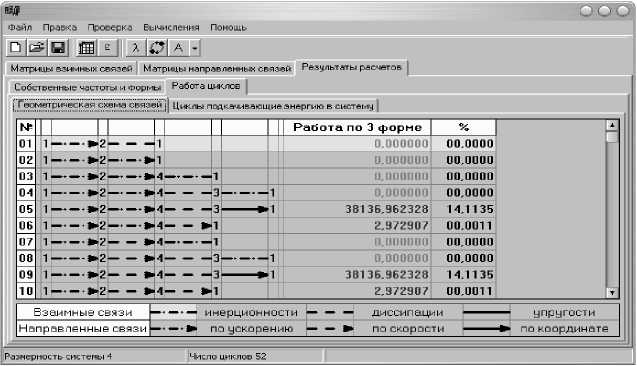
Рис. 3. Результаты исследований

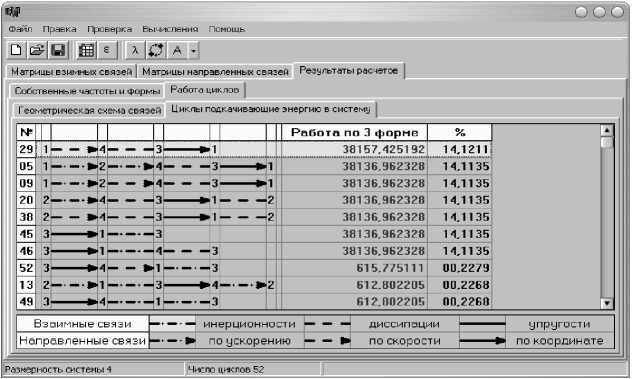
Рис. 4. Результаты исследований

Анализ результатов исследований показал, что наиболее чувствительными (наиболее ответственными за подкачку энергии в систему) являются 7 циклов из 52, у которых процентный вклад в суммарную работу направленных связей составляет 14%. Все эти циклы содержат направленную связь по координате, действующую со стороны осциллятора ψ на осциллятор Θ (где ψ – угловое перемещение указанных выше элементов передней подвески, а Θ – угловое перемещение кузова), которая вносит наибольший вклад в суммарную работу системы. С физической точки зрения этот механизм связан с силой увода кузова автомобиля при повороте колеса на угол ψ .

При повороте ведущего колеса со стороны дороги будет действовать сила реакции, в результате которой из-за взаимосвязи будут возбуждаться колебания кузова. Энергия этих колебаний является частью энергии, которая выделилась при сгорании топлива и передается колеблющемуся кузову в результате работы двигателя, взаимодействия дороги с колесами и связям между различными частями автомобиля. Что эти колебания самые опасные можно понять только с помощью разработанного комплекса. Но после того, как они найдены, можно понять их физическую природу и найти способы подавления автоколебаний.

Таким образом, работая с данным программным комплексом, студенты повышают уровень профессиональных компетенций как в области использования информационных технологий, так и в области применения естественнонаучных дисциплин для решения задач, связанных с математическим моделированием.

Заключение

Представленный в статье электронный контент в виде программного комплекса предназначен для формирования профессиональных компетенций бакалавров направления подготовки «Прикладная математика и информатика» в процессе построения адекватных математических моделей конкретных механических систем, которые обеспечивают необходимую для исследований простоту и сохраняют принципиальные особенности рассматриваемых систем, таких как наличие различных связей между степенями свободы, возможность линеаризации математической модели, определения круга задач, которые могут быть решены в таком приближении и т.д. Комплекс позволяет в интерактивном режиме исследовать причины самовозбуждения колебаний, строить геометрическую схему связей и находить наиболее значимые причины самовозбуждения, что помогает студентам глубже понять физические процессы, протекающие в автоколебательных системах, которые изучаются на различных этапах обучения.

Рассмотренный пример применения программного комплекса к изучению самовозбуждений колебаний в автомобиле обнаруживает возможность связать «академическое» изучение модели с «живым» восприятием объекта. Эта возможность позволяет, в частности, повышать мотивацию к обучению – студенты, обладающие развитым воображением, будут стараться осваивать методы, которые позволяют рассматривать и исследовать реальные объекты. В свою очередь у студентов с предпочтением к изучению абстрактных дисциплин развивается интерес к рассмотрению реальных практических объектов. Но и для первых и вторых это приводит к эффективному повышению уровня профессиональных компетенций.