Электрооптическая корректировка преобразования пучков Бесселя вдоль оси кристалла ниобата бария - стронция

Электрооптическое преобразование лазерных пучков может реализоваться двумя способами.

В первом способе формирование и преобразование происходит в комбинированном элементе, объединяющем дифракционную маску и управляющие электроды на поверхности электрооптического материала [1, 2].

Во втором случае формирование лазерного пучка осуществляется дифракционным оптическим элементом [3], а изменение его параметров производится в отдельной электроуправляемой части. Для управления произвольными лазерными пучками более удобен второй подход, обладающий большими возможностями как по генерации лазерных мод, так и по виду электроуправляемого воздействия (на фазу, поляризацию, амплитуду, направление распространения и др.).

Так, в работах [4, 5] было выполнено моделирование управления поляризацией, угловым и орбитальным моментом лазерных пучков Гаусса и Лаггера– Гаусса на основе электрооптического кристалла нио-бата бария – стронция Sr0,75Ba0,25Nb2O6 (SBN:75). Этот подход применим и к другим видам лазерных пучков, что расширяет возможности техники высокоразрешающей фотолитографии [6], оптической микроманипуляции [7, 8], лазерной абляции [9, 10]. Использование электрооптического эффекта позволяет создавать быстродействующие динамические элементы в отличие от сравнительно медленных методов температурного, хроматического и оптико-механического управления лазерными пучками Бесселя [11–13].

Целью работы являлось теоретическое исследование электроуправляемого преобразования лазерных пучков Бесселя нулевого порядка в вихревой пучок второго порядка. В качестве формирователя пучка Бесселя нулевого порядка рассматривается бинарная кольцевая решетка – дифракционный аксикон. В качестве преобразующего элемента выбран электрооптический кристалл ниобата бария – стронция Sr0,75Ba0,25Nb2O6 z-среза, обладающий высокой чувствительностью показателей преломления к напряженности электрического поля.

• 1.    Расчет статического преобразования пучков Бесселя

В работах [14, 15] были разработаны теоретические основы, описывающие периодическое модовое преобразование лазерных пучков при распространении оптической оси кристалла в непараксиальном режиме. Физические основы этого явления, связанные с интерференцией обыкновенного и необыкновенного лучей при острой фокусировке лазерного излучения в анизотропной среде, обсуждались в работе [16].

Наиболее интересные результаты были получены для однородно-поляризованных Бесселевых пучков:

„ , . ^f Bx ⁽ r , ф)) (Px ) _T A ,. X z-ex

^B m ( r , ф ) = 1 = 1 I ^J m ( ^k ° 0 r ) exP ( im ф ) , ⁽¹⁾ \ B y ⁽ r , ^{Ф )} ) \ p y )

где B_x ( r , ф ), B y ( r , ф ) - поперечные компоненты лазерного излучения, ( r , ф ) - полярные координаты, J_m ( x ) -функция Бесселя т- го порядка, к =2 л / % - волновое число, % - длина волны излучения в вакууме, с ₀ - параметр пучка, p x , p y – поляризационные коэффициенты.

Известно, что пучки Бесселя нулевого порядка можно формировать с помощью бинарной кольцевой решётки, представляющей собой дифракционный ак-сикон [17]:

т ( r ) = sgn [ cos ( к о ₀ r ) ] , (2) где sgn[ x ] – функция взятия знака.

В этом случае характеристики аксикона и параметр Бесселева пучка связываются через значение числовой апертуры аксикона:

о = 1/ d , (3) где d – период кольцевой решетки.

На рис. 1 а показана центральная часть (размером 70×70 мкм) бинарного дифракционного аксикона с периодом d =4 мкм, а также результаты моделирования формирования пучка Бесселя нулевого порядка с помощью такого аксикона в однородной среде с показателем преломления n =2,3 при освещении равномерным лазерным пучком с длиной волны 1 = 638,8 нм. В данном случае числовая апертура аксикона небольшая и составляет с₀ = 0,16. Как видно, пучок Бесселя сохраняет свою структуру на всем рассмотренном пути распространения за исключением роста интенсивности с увеличением z (рис. 1 г ). Последнее связано с фазовым характером аксикона [17] – при удалении от оптического элемента в формировании пучка начинают участвовать периферийные кольца, энергия от которых при освещении плоским пучком растет пропорционально площади колец.

Для пучков Бесселя нулевого порядка с круговой поляризацией py ± ipx было экспериментально показано [18], что при распространении вдоль оптической оси анизотропного кристалла будет происходит пе- риодическое преобразование пучка нулевого порядка в вихревой пучок второго порядка и обратно.

Комплексное распределение поля в случае формирования пучка Бесселя с помощью дифракционного аксикона (2) можно записать в виде [14, 15]:

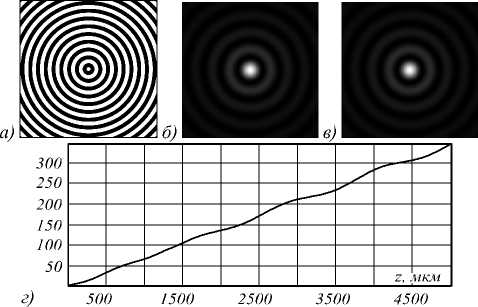
Рис. 1. Формирование пучка Бесселя нулевого порядка с помощью бинарного дифракционного аксикона с периодом d = 4 мкм (а) в однородной среде с показателем преломления n = 2,3 на расстоянии z = 1 мм (б) и z = 5 мм (в) (размер картин 16×16 мкм), а также график распределения интенсивности вдоль оптической оси z (г)

Е ( р , 0 , z ) = к¹

f VV2)

I ± if V2 7

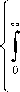
' SS ( к ро , 0 )

- SC ( к ро , 0 ) _ч 0

- SC ( к ро , 0 ) )

CC ( к ро , 0 ) exp [ ikz Y o ( о ) ] F ( о ) о d о +

CC ( к ро , 0 )

+f

SC ( к ро , 0 )

SC ( к ро , 0 )

SS ( к ро , 0 )

exp [ ikz Y _e ( о ) ] F ( о ) о d о

еоо еeYe (о)

C ( к ро , 0 )

е о оеeYe (о)

S ( к ро , 0 )

где

^

Fm (о) = f Т( r ) Jm ( кГо) r d r ,

Y о ( ° ) = 4 ⁶ о —° ² , Y e ( ° ) = V ^е о ^- ° ^{2 (} Е о / £ e ),

C ( t , 0 ) = iJ 1 ( t )cos ( 0 ) , S ( t , 0 ) = iJ 1 ( t )sin ( 0 ) , SC ( t , 0 ) = - (1/2) J ₂( t )sin ( 2 0 ) ,

CC ( t , 0 ) = (1/ 2) [ J ₀ ( t ) - J ₂ ( t ) cos ( 2 0 ) ] ,

SS ( t , 0 ) = (1/2) [ J o ( t ) + J ₂( t )cos ( 2 0 ) ] ,

где ео, £e - диэлектрические проницаемости кристалла для обыкновенного и необыкновенного лучей соот- ветственно.

Приближенно (без учета продольной компоненты и считая пучок Бесселя идеальным) распределение поперечной интенсивности в кристалле можно записать в виде [14, 15]:

I ( x , y ) = (1/2)| C|² J 2 ( к о о V x ² + y ²) + + (1/2)| S|² J 2 ( к о о V x² + y² ) ,

где C , S – условные величины, равные:

C = exp ( ikz Y _о ) + exp ( ikz Y _e ) ,

S = exp ( ikz Y _о ) - exp ( ikz Y _e ) .                         (9)

где z – толщина кристалла.

При этом интенсивность на оптической оси испытывает периодические изменения в зависимости от пройденного расстояния z в анизотропной среде:

I ( z ) - 1 + cos ( kz [ y e ( о о ) -Y о ( Ст о ) ] ) .                 (10)

Заметим, что формулы (8) и (10) описывают поведение в кристалле идеального пучка Бесселя, в случае использовании аксикона отличие будет состоять в линейном росте интенсивности, как пояснялось к рис. 1 г .

Используя выражения (4)–(7), выполним расчет преобразования для пучка Бесселя нулевого порядка, сформированного дифракционным аксиконом, при распространении в кристалле ниобата бария– стронция Sr_0,75Ba_0,25Nb₂O₆, имеющем обыкновенный и необыкновенный показатели преломления n_o = 2,3117, n_e = 2,2987 на длине волны λ = 632,8 нм. Результаты моделирования показаны на рис. 2, из которых видно, что при распространении в анизотропной среде пучок

Бесселя нулевого порядка преобразуется в пучок Бесселя второго порядка. Причем, судя по графику осевой интенсивности (рис. 2 е ), при толщине кристалла 5 мм происходит полное преобразование.

Однако из соображений компактности может потребоваться использование более тонкого кристалла. В этом случае можно увеличить числовую апертуру аксикона, формирующего пучок Бесселя. На рис. 3 показаны результаты моделирования для аксикона с периодом d =2 мкм, что соответствует увеличению числовой апертуры в два раза (с₀ = 0,32). Как видно, совершив два полных цикла, на выходе кристалла пучок возвращается в исходное состояние.

Заметим, что уменьшение периода аксикона может быть ограничено не только технологическими возможностями [19], но и предельной числовой апертурой [20], при которой в рассматриваемой оптической среде имеют место распространяющиеся волны.

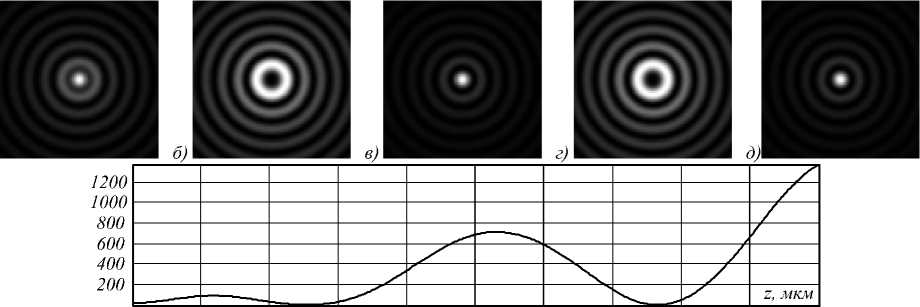
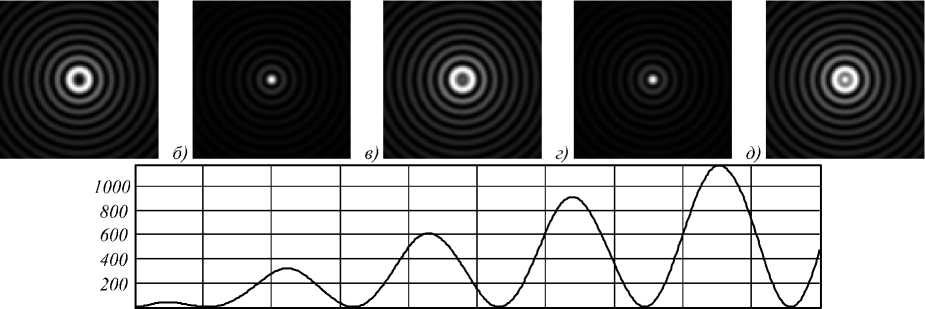
На рис. 4 показаны результаты моделирования для аксикона с периодом d =1,3 мкм (о₀ = 0,48). Такой ак-сикон может быть изготовлен с помощью установки круговой лазерной записи CLWS-200 на пределе технологических возможностей [21].

Из рис. 4 видно, что в кристалле происходит несколько циклов преобразования пучка Бесселя нулевого порядка в пучок второго порядка и обратно. Причем на выходе кристалла достигается некая средняя фаза преобразования. Чтобы получить некоторое определенное состояние на выходе кристалла, нужно подобрать/оп-тимизировать характеристики лазерного излучения, например, изменяя период аксикона или длину волны.

Для облегчения этой задачи вместо (10) можно воспользоваться параксиальным выражением [14, 15]

I ⁽ z ) ~ 1 + cos ( kz о 0 [ ( 1 - n o In2 ) /2 n₀ ^] )              ⁽¹¹⁾

и напрямую связать характеристики кристалла и параметры падающего на кристалл пучка с периодом преобразования. Таким образом, полное преобразование будет происходить для кристаллов толщиной:

h q = (2 % n o !< ( 1 - n 2/ n 2 ) ) ( 0,5 + q ) ,              (12)

q – целое положительное число.

Для рассматриваемого кристалла мы получаем следующее выражение для выбора периода аксикона:

d_q = 0,04^ h / ( q + 0,5 ) .                           (13)

В частности, чтобы в кристалле толщиной h = 5 мм произошло q =4 преобразования, период аксикона должен быть равен d = 1,33 мкм, т.е. немного больше, чем в случае, представленном на рис. 4.

пвиви

а) б) в) г) д)

е)

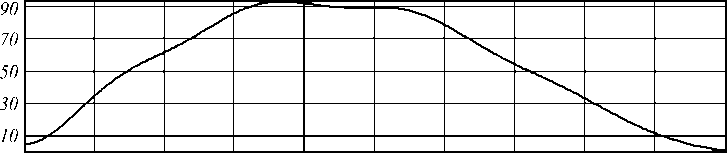
Рис. 2. Распространение пучка Бесселя нулевого порядка, сформированного с помощью аксикона с периодом d = 4 мкм вдоль оси кристалла ниобата бария–стронция, на расстояние z = 1 мм (а), z = 2 мм (б), z = 3 мм (в), z = 4 мм (г) и z = 5 мм (д) (размер картин 10×10 мкм), а также график распределения интенсивности вдоль оптической оси z (е)

е)

Рис. 3. Распространение пучка Бесселя нулевого порядка, сформированного с помощью аксикона с периодом d = 2 мкм вдоль оси кристалла ниобата бария – стронция, на расстояние z = 0,6 мм (а), z = 1,3 мм (б), z = 2,6 мм (в), z = 3,8 мм (г) и z = 5 мм (д) (размер картин 10×10 мкм), а также график распределения интенсивности вдоль оптической оси z (е)

е)          500   1000   1500   2000   2500   3000   3500   4000 4500 _, мкм

Рис. 4. Распространение пучка Бесселя нулевого порядка, сформированного с помощью аксикона с периодом d = 1,3 мкм вдоль оси кристалла ниобата бария–стронция, на расстояние z = 0,5 мм (а), z = 1 мм (б), z = 1,5 мм (в), z = 2 мм (г) и z = 2,5 мм (д) (размер картин 10×10 мкм), а также график распределения интенсивности вдоль оптической оси z (е)

2. Расчет динамического преобразования пучков Бесселя

Для достижения некоторого определенного состояния выходного пучка необходимо менять характеристики кристалла. Так, в работе [12] для изменения размерных и оптических характеристик кристалла использовался нагрев. Однако подход не слишком удобен из-за длительности процесса нагре-ва/остывания. Поэтому электрооптическое управление показателями преломления кристалла, обладающее существенно лучшим быстродействием, представляет особый интерес.

С этой целью выполним анализ применимости электрооптического кристалла ниобата бария–стронция Sr_0,75Ba_0,25Nb₂O₆. Используем случай продольного электрооптического эффекта E _z|| z и k || z , который реализуется для z -среза кристалла с прозрачными электродами, нанесенными на его входную и выходную поверхности. Расположение оптических элементов и ориентация кристалла поясняется на рис. 5.

Показатели преломления кристалла ниобата бария–стронция Sr 0,75 Ba 0,25 Nb 2 O 6 для продольного линейного электрооптического эффекта с E z || z и k || z имеют вид [22]:

n z ≈ n e - (1/2) n e ³ r 33 E z n z ≈ n e - (1/2) n e ³ r 33 E z , (14) где r 13 = 67∙10 ^–12, r 33 = 1340∙10 ^–12 – линейные электрооптические коэффициенты, м/В [23]. Напряженность электрического поля в формулах (11) вычисляется через напряжение на электродах U (В) и толщину кристалла h (м) следующим образом:

E_z = U / h . (15)

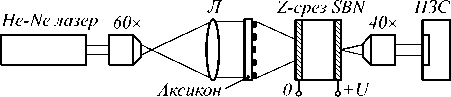
Для рассматриваемого кристалла толщиной h =5 мм с приложенным напряжением U =400 В изменения для показателей преломления составляют: ∆ n_o ≈ 3,25·10 ^–5 и ∆ n_e ≈ 6,51·10 ^–4 соответственно. На рис. 6 показаны результаты моделирования для аксикона с периодом d = 1,33 мкм в отсутствие напряжения и с приложенным к кристаллу напряжением U = - 400 В. Как видно, такого напряжения достаточно, чтобы согласовать характеристики лазерного излучения и кристалла и получить на выходе полностью преобразованный пучок.

а)

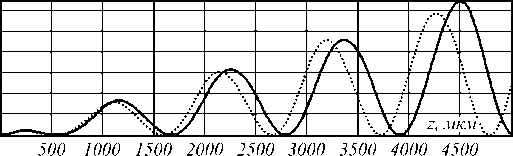
Рис. 5. Схема установки для электрооптического преобразования пучков Бесселя

Рис. 6. Распространение пучка Бесселя нулевого порядка, сформированного с помощью бинарного дифракционного аксикона с периодом d = 1,3 мкм вдоль оси кристалла ниобата бария–стронция: график распределения интенсивности

вдоль оптической оси z (без напряжения – точечная линия и с приложенным напряжением U = - 400 В – сплошная линия) и распределение на выходе кристалла (а) в отсутствие напряжения (б) и с приложенным к кристаллу напряжением

U = - 400 В (в); размер картин – 10×10 мкм

Из результатов расчетов следует, что полное преобразование пучка Бесселя нулевого порядка в пучок второго порядка происходит при напряжении около 400 В. Необходимая напряженность поля составляет E z ≈ 0,8 кВ/см, что меньше коэрцитивного поля E c ≈ 1кВ/см для SBN:75 [24].

Заключение

Теоретически исследованы особенности статического и динамического (электрооптического) преобразования пучков Бесселя вдоль оси кристалла Sr 0,75 Ba 0,25 Nb 2 O 6 .

Показана возможность электрически управляемого преобразования пучка Бесселя нулевого или второго порядков, а также их заданного сочетания в тонких кристаллах толщиной 5 мм за счет использования дифракционных аксиконов с высокой числовой апертурой (σ₀ ≈ 0,48). При рассмотренных параметрах напряженность электрического поля в кристалле не превосходит предельного (коэрцитивного) поля, что обеспечивает длительное сохранение его свойств.

Работа выполнена при поддержке Министерства образования и науки РФ, а также Российского фонда фундаментальных исследований (гранты РФФИ 1607-00825, 16-29-11698-офи_м).