Электропривод пружинный для борьбы с гололедом воздушных линий

В работе рассматривается один из вариантов борьбы с гололедом воздушных линий (ВЛ) в виде электромеханического устройства. Эта проблема является актуальной проблемой в современной энергетике.

Решение задачи

Электропружинный двигатель (ЭПРД) (см. рисунок) содержит полый корпус 1, внутри которого имеется ось 5 по всей длине корпуса. На ось свободно одеты инерционное кольцо 4 с возможностью перемещения вдоль нее, а также электропроводящая цилиндрическая пружина 3, которая одним концом жестко закреплена на головке корпуса, а другим связана с кольцом. В головке корпуса установлены блоки питания и управления 2,

имеющие автономное питание с целью создания импульсного напряжения. При получении импульса напряжения по электропроводящей пружине протекает ток, причем имеющий одинаковые направления в соседних ветвях. Между витками возникает притягивающая электродинамическая сила, вследствие чего пружина сжимается. Когда импульс тока равен нулю, пружина разжимается с кольцом и на корпус двигателя действует импульс реактивной движущейся силы. Дальше процесс повторяется и движение двигателя стабилизируется. Конструкция проста, надежна, удобна в эксплуатации. Такой двигатель найдет в перспективе в современной энергетике. Двигатели такой конструкции найдут широкое также применение в дви-гателестроении, машиностроении, приборостроении, медицине.

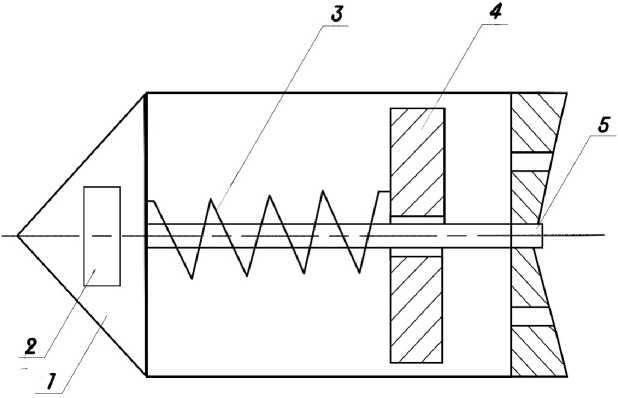
Рис. 1. Электропружинный двигатель

Электроэнергетика

Математическая модель ЭПРД выглядит следующим образом:

^{d 2 S}w ^{d r}w2

2 sw dtw

1     ^{d S}w

+ — x-w rw  d rw

₂ s_w r_w ²

, ¹ -ц ² S ^{2 s} _w = P--- x — w ,

E    d t

d s

+ 2 n Ex — +®0 Sw d t

= - 2 n A _вх sin ю t x s w (1) +

+ <

i ² ( "2"

VL

^dL 0 w + 2 NN ^dM 0 w , n

Z Z

dL _{0 w     1 1} dr _{0 w}

ew = Bо lw    + iR + di d t       dr

N

N

NN

+ TKl ■ 2У Т^к Lw

NN

Z L 0 w + 2 ZZ M 0 w , n

( N

+i I Z KLw V 1

di

iR +-- dr

N

NN ddw+2ZZ к

NN

-      ^dS w )

Mw , n i, I , , dt J

di

+— dt

Mw , n

-J

( N

+ B 0 il

s w ,

NN

Z K Lw S w + ZZ K мw , n S w I +

Z L о w + 2 ZZ M о w , n

di

+— dt

N

NN

Z K tw S w + ZZ Kmw , n S w

( N _ds NN      _ds )

+ i У к^—- + 2 У У Kмw_n—w ,

I Z dt ZZ Mw , n dt J ,

^s w L    = ⁰,

| rw = '0

^s w = N L = 1, rw = r 0

где s_w - радиальное перемещение w -го витка спирали; E - модуль упругости первого рода; ц - коэффициент Пуассона; n E - коэффициенты трения и демпфирования; ю ₀ - частота собственных колебаний; ю - частота вынужденных колебаний; r_w ‒ радиус w -го витка; l_w ‒ длина участка витка; B ₀ ‒ индукция магнитного поля; s_w (1) ‒ форма колебаний спирали магнитного поля; R ‒ активное сопротивление спирали; e ( t ) ‒ подводимое напряжение; L _{0 w} и M _{0 w} ‒ индуктивность и взаимоиндуктивность спирали в статическом состоянии; K_{L 0 w} , K_Min ‒ некоторые конструктивные постоянные.

Система дифференциальных уравнений с переменными коэффициентами представляет собой математическую модель обобщенной конструкции ЭПРД с пружинным вторичным элементом и позволяет исследовать характеристики ЭПРД.

В случае подключения электропроводящей механической пружины к синусоидальному источнику тока i = I m sinω t поставленная задача упрощается и выкладки становятся более наглядными. При этом уравнение колебания точки приведения системы будет иметь вид

x + 2 n Ex + ю0 x =

= Z S w (1) ^

_Im 2 ₂

Z dL ». + 2 Z dM »^ I+I Z K L, + 2 ZZ к м,., d^r 0w         d^r 0 w J V

sin ² ю t + B₀I m l sin ю t > .

Решение полученного уравнения находится как сумма решений вида:

z sw (1) im x1 =--------T"

^{4 M} пр ^ю 0

(у dhow + 2 у dM Ну к + 2у у к LVZ dr,w  Z ar,w J Vz w ZZ n

,

x 2 =

z s w, (1) i m

4 M ^Va - 4 q 2 ) + 16 D 2 q ²

dM 0 w dr _{0 w}

+ 2 у dM Ow У Гу к  2 у у к

Vw            V wn dr0 w J V

cos ( 2 ю t + ф ₂ ) , (3)

Zv ^S w ⁽¹⁾ I m ^B 0 l          /        \

x 3 =-------- ,                      - sin ( ю t + Ф з ) .

m пр ю 07 (1 - q ² ) ² + 4 d ² q ²

Суммарное результирующее усилие, развиваемое пружинным ЭПРД в режиме вибродвигателя, находится из второго закона Ньютона [1, 2] как произведение приведенной массы на ускорение точки приведения системы

A

F   M пр

V

d ² x 1 + d ² x ₂ dt ²     dt ²

d 2 x

+----:

dt

J

.

Исмагилов Ф.Р., Янгиров И.Ф., Максудов Д.В., Каланов Х.Х.

Общая формула для расчета характеристики электропружинного двигателя к   to2y m

F s   — ^s s_w (1) ^

to o

—

dl^w + 2У ydMw Uy K + 2 у ук lw            мwn dr0w          drow J V

7 (1 — 4 q 2 ) + 16 D ² qq .     I m B⁰       sin ( 2 to t + Ф₃)

7 (1 — q 2 ) 2 + 4 D ² q ²    '         '

- cos ( 2 to t + Ф 3 )

—

.

Из полученного выражения видно, что электродинамическое усилие двигателя представляет собой сумму сил с частотой питающего источника и двойной частотой источника. ЭПРД с пружинным вторичным элементом представляет также интерес как генератор низкочастотных колебаний, поэтому необходимо, чтобы выполнялось неравенство F _S (2 to ) ^^ F _{S M} ( to ) для исключения нежелательные вибрации с двойной частотой.

Этого можно добиться исключительно варьированием геометрических размеров пружины – шага витка, поперечных размеров, а также увеличением индукции первичного магнитного поля. В случае необходимости генерации колебаний двойной частоты необходимо исключить постоянное магнитное поле. Из этих соображений усилие, развиваемое электропружинным двигателем, находится в общем случае из соотношения

F S M

• = I m B 0 l ^ ,    ^S uw " '      sin ^(to t ⁺ ^ .

  
  

^to 0 7(1 — q 2 ) 2 + 4 d ² qq

Необходимо рассмотреть предельные частные случаи для режима двигателя.

• 1.    Аргумент функции Бесселя бесконечно малая величина. В этом случае соотношение для действую-

• щего усилия имеет вид

17-^ Г Д / ^R 1 R 0    V^{1    — Y}0        ^qq

F =    ImB01/

• ²        R 0 ^{— Y} 0 R 1 w = 1 ^Y W J (1 — q ² ) ² + 4 D ² q ²

или переходя к геометрическим размерам

N2    22

f-2± t r i   ^{R 0}  У r w r ^{0 q}_______

F      ImB0l  2   2 ^.

• ²    R 0 ^{— r} 0 w = 1   r w   7(1 — q ² ) ² + 4 d ² q²

  2. Аргумент функции Бесселя бесконечно большая величина. Действующее усилие в этом случае

  
  

  „ V2 _ .

  F = — I_mB_ol

  2 m 0

  
  

  E sin ^ ¹ 0 Y

  
  

  w

  
  

  —

  
  

  q ²

  
  

  . f l₀R  n)       f l₀R₀  n)    1(1-a2)2 +4D2a²

  sin -°-⁰- — — A cos '  — W ^q ) ^{+ 4 Dq}

  V R 1    4 J       V R 1    4 J

  
  
  
  

и для двухвитковой пружинной машины с бесконечно большими геометрическими размерами

F

V2 _ .

= —I_mB_ol

2 m 0

— q ² ) ² + 4 D ² qq

что совпадает с формулой, полученной ранее для расчета классических электрических машин в режиме вибрационных колебании с линейными геометрическими размерами [3, 4].

В соответствии с законом Ампера

2 n INBr = F _S ,                                                                                (12)

где N – число витков пружины; r – радиус витка пружины; B – индукция в пружине; I – ток в витках пружинного привода. Магнитная индукция, создаваемая в пружине, определяется выражением

B =

Fs

2 n IVr

а сила тока в витках механической пружины

I =     U вх

7R² + w ² 1 ² ,

где R – активное сопротивление цилиндрической пружины; U _вх – напряжение источника питания. При подстановке (14) в (13)

_{R P} 7R27 w¥

B = F_y--------

S  2nNUBX вх

.

Электроэнергетика

Чувствительность ЭПРД e=dB.                              (16)

dt

Малое перемещение ЭПРД за один такт работы F kx = F ^ x = 5 = — ,                (17)

k где k – жесткость пружины

Время перемещения ЭПРД по воздушной линии за один такт at2         2S

S = — ^ t = —,                (18)

2a из Fs = (M + m) a ускорение перемещения a =

Fs  ,

M + m ’

где М – масса установки; m – масса инерционного элемента.

Время работы пружинного привода

1 2 ( M + m )

t = \ k ’ а скорость движения ЭПРД по ВЛ

9 = F — ---_?.

k ( M + m )

Таким образом, получены все необходимые соотношения для проектирования ЭПРД по техническим требованиям испытуемого объекта.

Выводы

• 1.    Разработана оригинальная многофункциональная конструкция ЭПРД.

• 2.    Создана математическая модель ЭПРД, получены выражения для определения силовых приводных характеристик и чувствительности в зависимости от геометрических размеров и магнитных характеристик.

• 3.    Разработанная конструкция ЭПРД экономична, технологична и проста в эксплуатации относительно известных устройств по борьбе с гололедом ВЛ.