Электропроводящие полимерные композиты на эластичной волокнистой основе

Гибкие и растягивающиеся электропроводящие полимерные композиты применяются для изготовления различных сенсоров в исполнительных механизмах робототехники, автоматизированных агрегатах и машинах, в медицине. Интеллектуальные текстильные системы, с встроенными тензодатчиками на волокнистой основе используются для мониторинга движения человека [1, 2]. В работах [3–6] исследовали ткани высокой растяжимости для «умной одежды» из волокон с проводящим слоем или из смеси полимерных и металлических нитей. Эти материалы составляют основу так называемой «носимой электроники». Чувствительность волокнистого композита к деформации во многом зависит от структуры ткани и количества проводящих нитей. При исследовании тензочувствительно-сти электропроводящих композитов на основе металлизированных нитей в работе [6] показано увеличение чувствительности композита при скручивании нескольких нитей. Электропроводность полотна и его тензочувствительность увеличивается с увеличением числа нитей. Исследование зависимости электрической проводимости волокнистых композитов различной микро и макроструктуры, невозможно без определения механизма переноса электрически заряженных частиц в композиционном материале, содержащем диэлектрический полимер и электропроводящий наполнитель. Чаще всего наполнителем является металл или углерод в различных аллотропных формах (графит, графен, одностенные и многостенные нанотрубки, сажа). Существуют две основные теории, объясняющие зависимость электрической проводимости от деформации композиций «полимер-металл» или «полимер-углерод». Это тунельная теория пьезоэффекта [7] при афинной деформации полимерной матрицы и теория перколяции [8], т. е. теория объясняющая электропроводность композитов образованием и разрушением электропроводящих путей (цепочек контактирующих частиц наполнителя) [9]. В экспериментальном исследовании [10] показано, что проводящий путь, то есть длина цепочек контактирующих частиц наполнителя уменьшается при деформации растяжения вследствие роста микротрещин в материале. Электросопротивление растущих микротрещин имеет гораздо более высокие значения, чем сопротивление деформируемого пьезорезистивного материала. Трещины могут раскрываться и закрываться различным образом при деформации изгиба, кручения, растяжения и сжатия [11]. Электропроводность волокон и нитей существенно зависит от локализации электропроводящих частиц на их поверхности или в объеме. Расположение электропроводящих цепочек на поверхности или в объеме нитей определяет зависимость электрических свойств композитов от состояния окружающей среды (состав, температура, влажность). Предварительные исследования нитей с электропроводящими компонентами различной химической природы (металлы, соли металлов, углерод в различных аллотропных формах), показывают, что изменение температуры и влажности существенно влияют на удельное сопротивление проводящего волокна [12].

Цель работы – описание структуры и свойств новых полимерных композитов на волокнистой основе и оценка влияния температуры и влажности воздуха на их электропроводность.

Объекты и методы

В качестве объектов исследования использовали вещества и материалы промышленного производства, соответствующие российским и международным стандартам на их изготовление.

Для нанесения электропроводящего слоя на волокнистую основу композитов (хлопчатобумажный трикотаж) применили суспензию графита в пропаноле-2 с политетрафторэтиленом. Суспензия производится и реализуется на рынке в аэрозольной упаковке под маркой GRAPHIT 33/200. Качественный и количественный состав ингредиентов суспензии контролировали с помощью ИК Фурье спектрофотометра FT-801 и дифференциального сканирующего калориметра DSC 204 Phoenix фирмы NETZSCH. Соотношение графита и политетрафторэтилена в сухом остатке суспензии определили методом термогравиметрии на TGA/DSC 3 + (рисунок 1). После термодеструкции и удаления продуктов разложения полимера масса образца уменьшилась на 35% масс. Это изменение массы соответствует доле органических компонентов. Концентрация графита в сухом остатке около 65% масс.

Начало аффекта / the beginning of

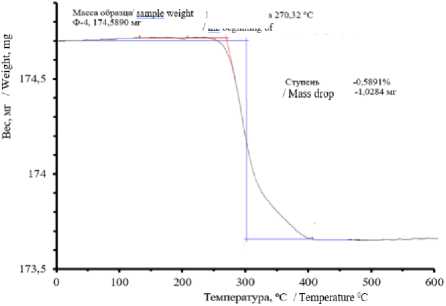
Рисунок 1. Кривая термогравиметрического анализа суспензии графита

Figure 1. Curve of thermogravimetric analysis of graphite suspension

Образцы для испытаний электропроводности размером 10 x 80 мм вырезали из трикотажного полотна, на поверхность которого нанесена дисперсия графита с политетрафторэтиленом распылением из аэрозольной упаковки. Количество графита на поверхности волокнистого материала контролировали по изменению массы полотна после сушки в вакуумном эксикаторе. Доля графита в композите 17 ± 0,7% масс.

Методика подготовки образцов электропроводящего волокнистого материала для электрофизических измерений включает следующие последовательные стадии:

Кондиционирование промышленного образца трикотажа в эксикаторе в течение 5 суток при температуре 22 ± 1о С и относительной влажности воздуха 30%,

Напыление дисперсии графита с политетрафторэтиленом в пропаноле-2 на образцы из аэрозольной упаковки с расстояния 10 см, в течение 5 секунд, со скоростью перемещения сопла вдоль образца 0,07 м/с.;

Вырезание лентообразных образцов с покрытием, содержащим графит;

Сушка образцов с покрытием в лабораторном помещении при температуре 20 ± 1о С и относительной влажности воздуха 30% до постоянной массы;

Измерение массы 10-ти идентичных образцов на аналитических весах с точностью 0,0001 г. и вычислением среднего значения;

Наклеивание электродов из медной фольги электропроводящим клеем контактол марки Keller на поверхность лент, покрытых графитом (рисунок 1);

Кондиционирование образцов в эксикаторе перед проведением механических испытаний и измерения электрического сопротивления при температуре 10 и 700 С и относительной влажности воздуха 45% и 100%.

Двухслойный датчик деформации собирают из трикотажа с электропроводящим покрытием, следующим образом. Размещают отрезки ленты равной длины зеркально и укладывают отрезки попарно друг на друга, т. е. производят дублирование проводящего слоя внутри трикотажа. Между концами отрезков укладывают плоский электрод из медной фольги с проводами и таким образом производят электрическое соединение слоя графита с источником постоянного тока для измерения электрического сопротивления (рисунок 3).

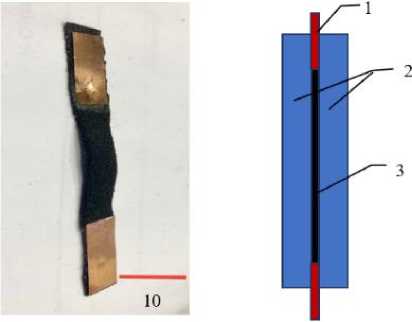
(a)                              (b)

Рисунок 2. Образец полимерного композита для испытаний электропроводности. (a) фотография, (b) схема сборки двуслойного датчика деформации: 1 – электроды (медная фольга); 2 – слои трикотажа; 3 – слой графита Figure 2. Sample of polymer composite for electrical conductivity testing. (a) photo, (b) assembly diagram of a two-layer deformation sensor: 1 – electrodes (copper foil); 2 – layers of knitwear; 3 – a layer of graphite

Рисунок 3. Фотография дублированного образца трикотажа с электропроводящим покрытием в зажимах устройства для циклической деформации Figure 3. Photo of a duplicated sample of knitwear with an electrically conductive coating in the clamps of the device for cyclic deformation

Результаты и обсуждение

Волокнистые композиты состоят из трикотажной основы, коллоидного графита и тонких слоев высокомолекулярных соединений. Электропроводящие частицы коллоидного графита заполняют пространство между волокнами и удерживаются на поверхности нитей силами адгезии.

Выбор вида переплетения нитей волокнистой основы тензорезисторов и ориентации вырезания лент относительно направления расположения нитей основы, обосновано в работе.

Композиты после кондиционирования в разных условиях были испытаны путем циклической деформации с постоянной скоростью до относительного удлинения до 50%.

Электропроводность ленты трикотажа со слоем графита шириной 10 мм снижается на десятичный порядок при удлинении до 50% (рисунок 4).

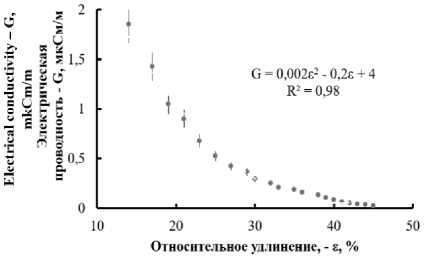
Relative elongation, - e, %

Рисунок 4. 3ависимость электропроводности композита от деформации

Figure 4. Dependence of the electrical conductivity of the composite on deformation

Образцы электропроводящих композитов деформировали при температуре 25 ± 2ºС в воздушной среде с фиксированной относительной влажностью. Результаты статистической

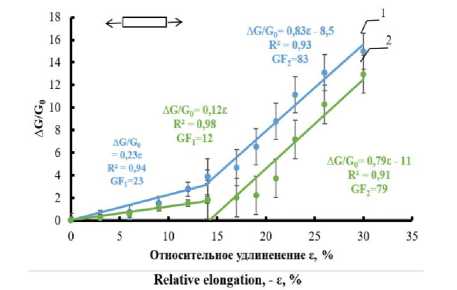
Рисунок 5. Относительное изменение электропроводности лент композита при растяжении. Влажность воздуха: 1 – 45%, 2 – 100%

Figure 5. The relative change in the electrical conductivity of the composite tapes during stretching. Humidity: 1 – 45%, 2 – 100% обработки значений электропроводимости трикотажной ленты при растяжении, нормированных по величине электропроводимости недеформированного трикотажа с покрытием представлены на рисунке 5.

По тангенсу угла наклона прямолинейных участков зависимости изменения электропроводности композитов от относительной деформации рассчитаны калибровочные коэффициенты (GF), определяющие деформационную чувствительность датчиков [13–15].

Для повышения точности аппроксимации экспериментальных данных линейными функциями массив результатов измерений электропроводности трикотажа при малых деформациях растяжения (0 ÷ 15%) представлен на отдельном графике (рисунок 6). Этот диапазон деформации имеет большее практическое значение при применении композитов в качестве сенсоров измерительных средств малых деформаций, например, применяемых при медицинском контроле мимики, дыхания и сердцебиения человека в плотно прилегающей одежде [16, 17]

Видно, что увеличение влажности воздуха снижает деформационную чувствительность композитов в 2 раза при малых удлинениях.

Для определения причины многократного изменения чувствительности электропроводности композитов к деформации при растяжении свыше 15%, произведена оптическая микрофотография поверхности с построением 3D модели рельефа и сечения полотна вдоль нитей основы трикотажа (рисунок 7). По форме сечения видно, что нити основы изогнуты, поэтому трикотажное полотно легко деформируется до определённого удлинения за счёт их распрямления. Правомерно предположить, что при распрямлении нитей монолитность и электропроводность слоя графита на их поверхности не нарушается.

Рисунок 7. 3-D изображение поверхности и профиль сечения трикотажа вдоль нитей основы

Figure 7. 3-D image of the surface and cross-section profile of knitwear along the warp threads

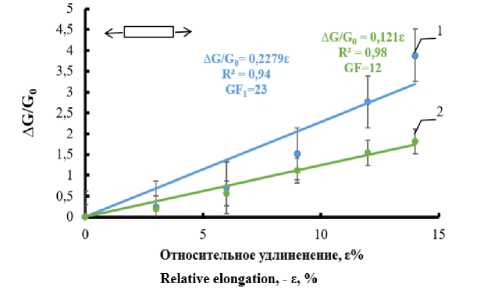
Рисунок 6. Относительное изменение электропроводности лент композита при растяжении. Влажность воздуха: 1 – 45%, 2 – 100%

Figure 6. Relative change in electrical conductivity of composite tapes during stretching. Humidity: 1 – 45%, 2 – 100%

Сравнение длины извилистой линии профиля (рисунок 7) с габаритами образца трикотажа подтверждает предположения о том, что при растяжении до 15% происходит выпрямление нитей, которое не значительно влияет на электропроводность композита. При деформировании трикотажа свыше 15% электропроводность композита резко возрастает за счет увеличения длины и площади внешней поверхности нитей, растрескивания электропроводящего слоя на поверхности и нарушения контакта между отдельными частицами графита.

При эластичном сокращении трикотажа контакт между частицами графита восстанавливается и электропроводность увеличивается. Чувствительность волокнистого композита к деформации оценивается калибровочным коэффициентом (GF), который на лабораторных образцах, полученных по патенту не уступает опубликованным значениям калибровочных коэффициентов (GF) композитов с различными электропроводящими наполнителями [18–21].

Зависимость электропроводности от направления деформации композитов т. е. от растяжения или сокращения не существенна и определяется лишь её величиной. Калибровочные коэффициенты деформации композитов различной влажности при деформациях свыше 15% велики и достигают 75–117 (рисунок 8, 9).

Таблица 1.

Расчеты калибровочных коэффициентов (GF) зарубежных и отечественных исследователей

Table 1.

Calculations of calibration coefficients (GF) of foreign domestic researchers

Публикации/ Publications	GF
19. С, Mattmann, и др. Датчик для измерения деформации в текстильных изделиях, Sensors, 2008, 8,3719. 19. С. Mettmann, et al. Sensor for measuring deformation in textiles, Sensors, 2008, 8,3719	<20
20. Hu. ¥.,« др., Недорогой, пригодный для печати и растягивающийся тензодатчик на основе высоколр.оводящт эластичных композитов с настраиваемой чувствительностью для мониторинга движений человека. Nano Res. 2018,11,1938-1955 20. Hu. ¥., et al., An inexpensive, printable and stretchable strain gauge based on highly conductive elastic composites with adjustable sensitivity for monitoring human movements. Nano Bus. 2018,11. 1938-1955	<100
21.Xu Xiao , и др., Датчики высокой деформации на основе гибких пленок полистирола пй^идизрвщшы^ нтоп^оволркоп и ZnO. Advanced materials. 201 i. 23,45,5440-5444 21.Xu Xiao, et al, High strain sensors based on flexible polystyrene films hybridized with nanowire and ZnO, Advanced materials, 2011. 23,45, 5440-5444	<120
22. E V Boyko и др., Зависимость электрического сопротивления графена от механической деформации. J Phys.: Conf. Ser. 1677 01212 5,2020                     '    . 22. Е V Boyko et al., Dependence of graphene electrical resistance	<34
on mechanical deformation. J. Phys.: Conf. Ser. 1677 012125, 2020

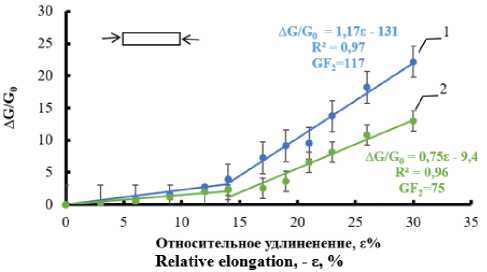
Рисунок 8. Изменение электропроводности лент композита при сокращении. Влажность воздуха: 1 – 45%, 2 – 100%

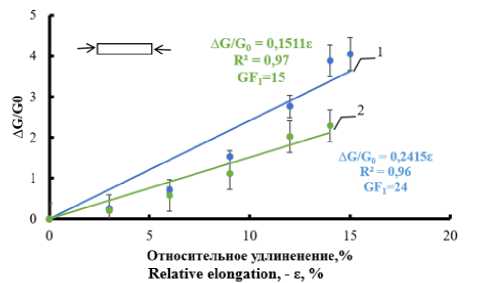
Рисунок 9. Изменение электропроводности лент композита при сокращении. Влажность воздуха: 1 – 45%, 2 – 100%

• Figure 8.    Change in electrical conductivity of composite tapes during reduction. Air humidity: 1 – 45%, 2 – 100%.

• Figure 9.    Change in electrical conductivity of composite tapes during reduction. Air humidity: 1 – 45%, 2 – 100%

На рисунке 6 и 9 показано, относительное изменение электропроводности, эластичных волокнистых композитов при растяжении и сокращении, после кондиционирования в течение 72 часов в атмосфере с различной влажностью воздуха, при температуре 300 C. Видно, что электропроводность и деформационная чувствительность при растяжении и сокращении композитов существенно зависит от относительной влажности воздуха при удлинении более 15%. Калибровочный коэффициент GF при малых деформациях растяжения до 15% и при деформации до 30% различается в 2 раза, но снижается при увеличении влажности воздуха.

Снижение чувствительности электропроводности композитов к циклическим деформациям (растяжения и сокращения) при высокой влажности воздуха обусловлено пластифицирующим действием воды на слой дисперсии графита. Слой дисперсии графита с ПТФЭ на поверхности нитей меньше растрескивается во влажной атмосфере чем в сухой, а микрорастрескивание электропроводящих полимерных композиций с графитом, как доказано в работе [10] является основной причиной увеличения их электросопротивления.

Для практического применения композитов в «умной одежде» представляет интерес исследование чувствительности электропроводности

Lozitskaya A.V. et al., Proceedings of VSUET, 2023, vol. 8 5 , no. датчиков деформации в диапазоне температур воздуха, при которых как правило происходит эксплуатация специальной верхней одежды. Для определения влияния температуры на элек-

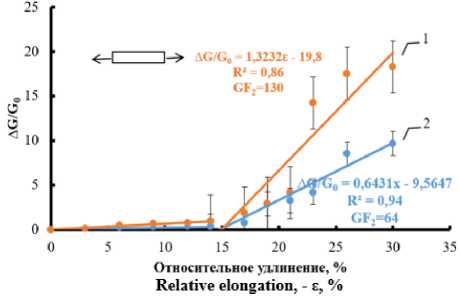
Рисунок 10. Изменение электропроводности лент композита при растяжении до 30% в холодном и горячем воздухе. Температура: 1 – 70 °С; 2 – 10 °С

Figure 10. Change in the electrical conductivity of composite tapes when stretched up to 30% in cold and hot air. Temperature: 11 – 70 °С; 2 – 10 °С

трические свойства волокнистых композитов проводили измерения сопротивления образцов в горячем и холодном воздухе и определяли деформационную чувствительность при 10 и 70 °С.

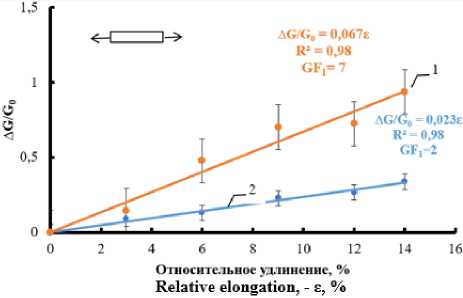
Рисунок 11. Изменение электропроводности лент композита при растяжении до 15% в холодном и горячем воздухе. Температура: 1 – 70 °С; 2 – 10 °С

Figure 11. Change in the electrical conductivity of composite tapes when stretched up to 15% in cold and hot air. Temperature: 1 – 70 °С; 2 – 10 °С

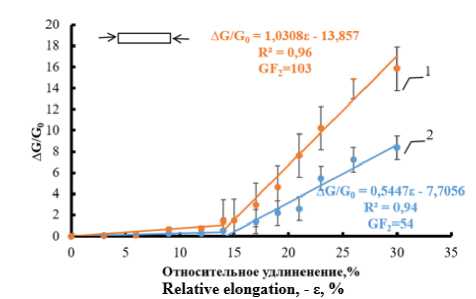
Рисунок 12. Изменение электропроводности лент композита при сокращении до 30%. Температура: 1 – 70 °С; 2 – 10 °С

Figure 12. Change in the electrical conductivity of composite tapes with a reduction of up to 30%. Temperature: 1 – 70 °С; 2 – 10 °С

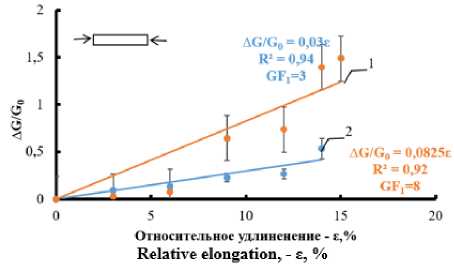
Рисунок 13. Изменение электропроводности лент композита при сокращении до 15%. Температура: 1 – 70 °С; 2 – 10 °С

Figure 13. Change in the electrical conductivity of composite tapes with a reduction of up to 15%. Temperature: 1 – 70 °С; 2 – 10 °С

На рисунках 10÷13 показано изменение электропроводности лент волокнистых композитов, в условиях нормальной влажности воздуха 45% и при температуре 70 и 10 °С. Видно, что при температуре воздуха 70 °С деформационная чувствительность (GF) при растяжении и сокращении возрастает в два-три раза. Особенно заметно увеличение чувствительности композитов к повышению температуры воздуха при циклической деформации менее 15%, при которой происходит распрямление нитей трикотажа.

Как известно [22] сопротивление проводников с металлическим типом электропроводности при нагревании увеличивается. Аналогичная зависимость от температуры электропроводности полимерных композитов дисперсно наполненных металлами и графитом установлены в работе [23].

Так как электрические свойства волокнистых композитов, определяются электропроводностью слоя дисперсии графита с политетрафторэтиленом, то правомерно ожидать снижение электропроводности при повышении температуры воздуха и ее повышение при охлаждении.

Из экспериментально полученных закономерностей изменения электропроводности волокнистых композитов при циклических деформациях, (рисунок 4–12) и сравнительной оценки вычисленных коэффициентов GF можно заключить, что трикотажное полотно с покрытием из дисперсии графита с ПТФЭ при растяжении и сокращении в горячем и сухом воздухе имеют значительно большую чувствительность к растяжению и сокращению чем во влажной и холодной атмосфере.

Для определения истинной тензочувстви-тельности, т. е. характеристики зависимости электропроводности композита от механического напряжения [15] необходимо получить сведения о механических свойствах волокнистых композитов, т. е. иметь экспериментальные значения силы, возникающей в материале на стадиях растяжения и эластического сокращения. При механических испытаниях композита на растя- жение можно достоверно измерить силу натяжения ленты известной ширины, а величину напряжения характеризовать условным значением нагрузки, так как точное значение толщины

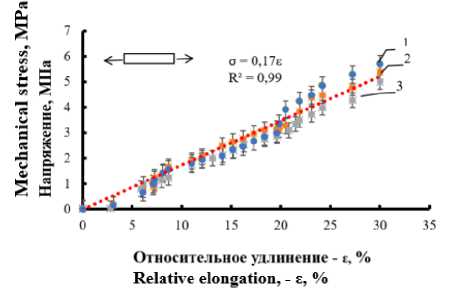
Рисунок 14. Диаграмма растяжения композитов: 1, 2, 3 – циклы деформации

Figure 14. Stretching diagram of composites: 1, 2, 3 – deformation cycles

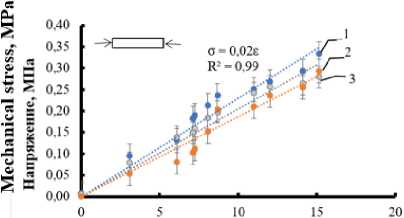
Относительное удлинение, е%

Relative elongation, - е, %

Рисунок 16. Диаграмма сокращения композитов при малых деформациях: 1, 2, 3 – циклы деформации

Figure 16. Diagram of the reduction of composites under small deformations: 1, 2, 3 – deformation cycles

По диаграммам растяжения видно, что механические свойства композитов на стадии удлинения могут быть охарактеризованы одной величиной условного модуля упругости (рисунок 14) – примерно 17 МПа. На стадии сокращения условный модуль упругости композита составляет 2 МПа, при деформации менее 15% и 30 МПа при больших удлинениях.

Тензочувствительность композита к механическому напряжению QF при деформации растяжения вычисляется по формуле:

QF =ΔG/G0, [Па-1] Δσ трикотажа определить невозможно. Функции условного напряжения (нагрузки) от относительного удлинения при циклическом деформировании композитов в процессах растяжения и сокращения качественно различны (рисунок 14 и 15).

При растяжении напряжение в композиционном материале монотонно увеличивается и может быть описано уравнением прямой линии с постоянным условным модулем упругости (рисунок 13). При сокращении изменения напряжения может быть описано двумя модулями, малым в диапазоне 0÷15% (рисунок 15) и большим (рисунок 14) в диапазоне свыше 15%.

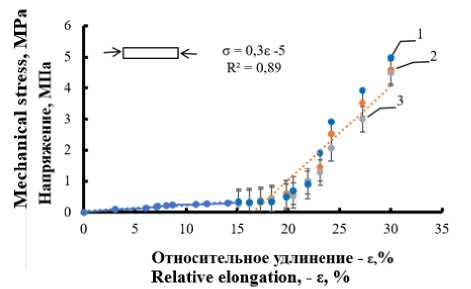
Рисунок 15. Диаграмма сокращения композитов: 1, 2, 3 – циклы деформации

Figure 15. Composite reduction diagram: 1, 2, 3 – deformation cycles

В таблицу 2 сведены результаты вычисления тензо- и деформационной чувствительности композитов на основе трикотажа при различной температуре и влажности.

Таблица 2. Деформационная чувствительность (GF) и тензочувствительности (QF) композитов

Table 2.

Strain sensitivity (GF) and strain sensitivity (QF) of composites

Условия деформирования / Deformation conditions	Деформационная чувствительность/ Deformation sensitivity GF		Тензочувствительность / Strain sensitivity QF. кПа1
	GF,	GF,	QF,	QF.
Растяжение в диапазоне относительной деформации, % / Stretching in the range of relative deformation, %
Температура(°С) Temperature(°C)	0+15	15+30	0+15	15+30
10*2	2*0.5	64*4	117*6	3764±7
70*3	7*1	130*5	411*6	7647*8
Влажность воздуха /Air humidity, %
45*3	23*3	83*5	1353*6	4882*7
100	12*2	79*4	705*6	4647*7
Сокращение в диапазоне относительной деформации, % Reduction in the range of relative deformation, %
Температура (°C) Tempera hire (°C)	15+0	30+15	15+0	30+15
10*1	3*0.8	54*4	1500±6	1800
70*1	8*1	103*5	4000±7	3433
Влажность воздуха /Air humidity, %
45*3	24*3	117*5	12000*9	3900*7
100	15*2	75*4	7500*8	2500*7

На рисунке 17 показано изменение электропроводности композита на основе трикотажа при многократном растяжении. Видно, что первый цикл деформации имеет значительно большее изменение электропроводности при деформации до 30%, чем последующие циклы. Это различие имеет место как при растяжении, так и при сокращении. Второе и далее (до 100 раз) циклическое деформирование композита на основе трикотажа, покрытого графитом, не влияет на его структуру и свойства. Достигается устойчивое состояние композита со стабильно воспроизводимыми и идентичными значениями деформационной чувствительности (GF 1 и GF 2 ) и тензочувствительности (QF 1 , QF2) во всем исследованном диапазоне удлинений.

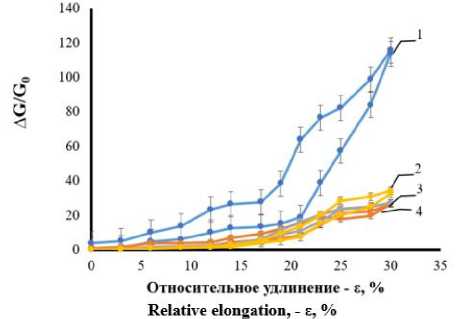
Рисунок 17. Изменение электропроводности композита при циклической деформации: 1, 2, 3, 4 – циклы

Figure 17. Change in the electrical conductivity of the composite during cyclic deformation: 1, 2, 3, 4 – cycles

Результаты испытаний, включающие первый цикл обратимой деформации трикотажа и 3 последующих цикла гистерезиса представлены в таблице 3.

Гистерезис (h) (таблица 3) рассчитан по формуле Симпсона [18] с вычислением интеграла функции изменения электропроводности от деформации:

ΔGG(ε↓)dε-∫bΔGG(ε↑)dε h =              a

∫ΔGG(ε↓)dε

a

× 100,

где, s - относительная деформация, A G/ G - изменение электропроводности, a, b – пределы изменения электропроводности Δ GG при деформации ε ↨ – направление деформации (растяжение, сжатие)

Таблица 3.

Гистерезис электропроводности при циклических деформациях

Table 3.

Hysteresis of electrical conductivity under cyclic deformations

Номер цикла деформирования при измерении электропроводности / Number of the deformation cycle when measuring electrical conductivity	Гистерезис (h), % Hysteresis (h), %
1	50 ±0,5
2	3,8 ± 0,3
3	3,4 ± 02
4	3,4 ± 0,2

Малый гистерезис становится особенно важным, когда композиты используются в качестве датчика циклической деформации динамической нагрузки, например, при изготовлении элементов носимой электроники. Превышение гистерезиса свыше 6% приводит к накоплению пластической деформации и необратимому снижению чувствительности композита к деформации и динамической нагрузке.

Заключение

Разработана технология изготовления и исследованы электромеханические свойства слоистых волокнистых композитов на основе трикотажа и дисперсии графита, предназначенных для изготовления датчиков деформации и напряжения, применяемых в «носимой электронике», в робототехнике и медицине. Установлена различная деформационная и тензочувствитель-ность композитов в диапазонах малых и значительных растяжений, при различной температуре и влажности воздуха. Деформационная чувствительность достигает 130, а тензочувствитель-ность 12МПа-1, что на порядок превышает чувствительность к напряжению известных полимерных композитов с различным электропроводящими наполнителями.

Температура и влажность влияют на электромеханические свойства эластичных волокнистых композитов с графитом. При растяжении до 15% калибровочный коэффициент GF снижается в 2 раза при 100% влажности.

Установлено различное влияние температуры воздуха в диапазоне 10 °С ÷70 °С на деформационную и тензочувствительность при циклическом деформировании до 15% и 30%. Наличие двух диапазонов деформационной чувствительности обусловлено различием механизмов удлинения трикотажа за счет распрямления и растяжения нитей.