Электропроводность и полупроводниковые параметры биологических мембран

Исследования механизмов электронного транспорта в биологическом материале начались с изучения фотоиндуцированного окисления цитохромов в фотосинтезирующих бактериях Chromatium, т. е. переноса электронов от цитохрома к реакционному центру хлорофилла. Низкотемпературные измерения далее позволили, во-первых, детально изучить температурную зависимость проводимости и, во-вторых, обнаружить туннелирование электронов. Уже к 1960 г. Чанс и Нишимура [1] обнаружили передачу электронов в дыхательной цепи ниже температуры жидкого азота. В 1966 г. Де Во и Чанс [2] исследовали температурную зависимость проводимости цитохромоксидазы в диапазоне 31–298 К и выяснили, что при низких температурах (< 65 К) начинается туннелирование электронов, тогда как при высоких температурах преобладает полупроводниковый характер температурной зависимости проводимости, т. е. возрастание по аррениусовскому закону exp (-Ea I kT). Немного позже результаты исследований температурной зависимости электропроводности были суммированы Йортнером [3] в виде следующих положений: измеренное время полуокисления цитохрома при температуре 4.5 К равно т^2 = 2.3 мс ; время τ1 2 практически постоянно в температурном диапазоне 4.5 ^ 100К, а энергия активации проводимости в этом температурном диапазоне составляет не более 3.5 • 10-3 эВ; в диапазоне 100300 К время τ1 2 уменьшается от 2.3 мс до 2 мкс; температурная зависимость времени τ1 2 в диапазоне 100–300 К соответствует энергии активации 0.14 ±0.03 эВ, т. е. примерно 5.5 kT при температуре T = 300 К.

Стало ясно [4], что для переноса электронов нет необходимости в строгой периодической решетке. Необходимо только достаточно сильное взаимодействие переносчиков, способствующее коллективизации свободных электронных состояний.

Перенос электронов начал активно изучаться при исследованиях химических реакций в растворах, а затем и в гетерогенных средах и, в частности, в биологических мембранах, где донорноакцепторные пары хорошо структурированы в пространстве и организованы во времени.

Биологические мембраны природного и искусственного происхождения начали в последнее время использоваться для построения измерительных систем (биосенсоров). Например, для регистрации внеклеточных сигналов [5, 6] от электро-генных раковых (HL-1) и эмбриональных почечных (HEK293) клеток путем прямого электролитического контакта с плавающими затворами комплементарной пары полевых транзисторов [5]. Сверхминиатюрные алмазные транзисторы использовались [6] для измерений ионного обмена клеток также путем прямого электролитического контакта. Известно [7], что в мембранах некоторых электрохимически активных бактерий, относящихся к семейству Exoelectrogens, имеются цепи переноса электронов, альтернативные основной (дыхательной) цепи, способные передавать электроны на любой внешний акцептор, например металлы. Это свойство может быть использовано для антикоррозионной защиты. Уже сравнительно давно на основе предположения Уильяма Шокли о полупроводниковых свойствах нервных волокон возник интерес к нейропротезированию [8].

ИСХОДНЫЕ ПОЛОЖЕНИЯ

Исходной точкой для анализа электронного переноса были исследования Фёрстера [9] миграции энергии возбуждения по частотным составляющим спектров флуоресценции посредством ди-поль-дипольных взаимодействий. Немного позже туннельный перенос электронов для сильного перекрытия орбиталей при расстоянии между донором и акцептором не более 10-15 А был исследован Декстером [10].

Константа скорости бимолекулярной реакции в растворе (частота столкновений реагентов), первоначально полученная при классическом описании методами статистической механики жидкостей, записывалась [11] общим выражением вида

K = k(r)Act2 exp (-АG*/RT), где k(r) — средняя вероятность однократного электронного переноса в донорно-акцепторной паре, экспоненциально зависящая от расстояния r при больших расстояниях и близкая к единице при малых расстояниях; фактор Aσ2 определяет частоту столкновений; АG — свободная энергия реакции; кроме того,

А G * = ( X! 4 ) [ 1 + ( А G ET / X ) ] 2

( X — энергия реорганизации; А G ET — движущая сила переноса). Отметим, что значение стандартной свободной энергии А G ⁰ обычно известно для реакций в растворе, но гораздо менее известно для мембранных донорно-акцепторных пар.

Квантовомеханическое описание переноса электрона в гомогенной среде (реагенты плюс растворитель) исходно было записано в форме [11]

K = п H Ab(fc), й где (FC) — фактор, определяемый адиабатным принципом Франка—Кондона о неизменности положения взаимодействующих ядер, т. е. сумма произведений интегралов перекрытия вибрационных и сольватных волновых функций для реагентов и таких же интегралов для продуктов реакции; HAB — матричный элемент связи электронных состояний реагентов и продуктов.

Позже для полуклассического описания обмена электронами в обратимой химической реакции в теории Маркуса [12] было получено основное уравнение для неадиабатического электронного переноса

2 п    |V f|            ( ^X + ^А G ) 2

k_F = exp --, ^ET й ^nXk J TT ^р[    4Xk_BT _]

которое представляет собой квантовомеханический аналог уравнения Аррениуса. Предэкспонен-циальный множитель в уравнении имеет размерность |^c-1 J и означает число электронных переходов в секунду, т. е. электрический ток в донорноакцепторной паре переносчиков. Таким образом, для однонаправленного переноса электронов это уравнение является аналогом вольт-амперной характеристики перехода. Скорость передачи электронов определяется суммой энергии реорганизации λ, т. е. потенциальной энергии, характеризующей конфигурационные изменения электронных переносчиков в акте переноса, и изменением гиббсовской свободной энергии ΔG, рассматриваемой как термодинамическая составляющая движущей силы электронного переноса. Кинетическая составляющая энергии переноса определяется обменным взаимодействием электрона с колебаниями атомов гипотетической решетки (белка). Матричный элемент Vif    определяет раз ность энергетических уровней электрона в начальном (i) состоянии (DA) и конечном (f) состоянии (D+A–). В течение последних десятилетий уравнение Маркуса использовалось в разнообразных приложениях, касающихся электронного переноса [13].

Полуклассическая гауссовская аппроксимация [14] вероятности переноса электрона для локально организованной в мембране донорно-акцепторной пары, адекватно описывающая процесс для достаточно высоких температур [11], определяется соотношением

I ^А E с I

ш 2п   Vda (R)         I to"S)

sc = ^  -S(2V + , / p - 2S(2V +1) ’ где v = [exp(й^(kBT))-1] = kBT/(ha) (при T = = 300 К); АЕ/(ha) = P (AE — энергия активации проводимости); S = Er/(ha) (Er — энергия реорганизации, т. е. восстановления равновесных, или точнее исходных для каждого акта переноса конфигураций реагентов и продуктов); параметр S характеризует силу связи; условие S » 1 определяет сильную связь; частота ω принадлежит полосе собственных частот (нормальных колебаний) осцилляторов биологической среды, квантами которой ħω возбуждается перенос.

Потенциальная энергия реорганизации складывается из двух компонент, первая из которых определяется изменением длин упругих связей реагентов, а вторая — изменением поляризации всех групп, участвующих в переносе.

При расстоянии между активными центрами электронных переносчиков в пределах 5–20 Å или менее этого (например, для реакционных центров мембранных фотосистем) трансмембранный ток имеет туннельную природу. Иногда считалось (В.И. Гольданский), что туннельный эффект лежит в самой основе происхождения жизни.

Общие свойства электронпереносящей цепи, необходимые для дальнейшего анализа, могут быть кратко сформулированы в виде следующих известных положений.

Мембранная цепь переноса электронов (дыхательная цепь животной клетки) включает не менее 15 реакций для генерации и транспорта окислительно-восстановительных эквивалентов (H+, e) и производства энергии (фосфорилирования АДФ). Принципиальным, хотя и грубым, аналогом биологической системы электронного транспорта может служить водородно-кислородный топливный элемент Гроува (W.R. Grove, 1839). Здесь на одном электроде (аноде) водород каталитически превращается в компоненты (H+, e); протоны (в твердом полимерном электролите) и электроны (во внешней электрической цепи) перемещаются к другому электроду (катоду), где в присутствии кислорода образуется вода. Функцию проводника внешней электрической цепи в биологической мембране выполняет цепь белков-переносчиков, локализованная в основном в теле мембраны. Кофактором электронного переноса, но не легирующей примесью, служит единственный атом металла (Fe, Cu). Трансмембранная цепь переноса электронов начинается от источника (H+, e) (НАД∙Н) и заканчивается терминальным акцептором электронов (1/2)O2. Лимитирующими факторами электронного переноса являются поступление водорода и кислорода, а также доступность АДФ и Фн (неорганический фосфат). Кинетические свойства цепи, исследование которых имеет длинную и противоречивую историю, определяются временем полуокисления τ1/2 переносчиков (кинетика первого порядка). В последующих расчетах будут использованы считающиеся достаточно достоверными [15] значения τ1/2 = 0.51 мс для звена a → a3 и τ1/2 = 0.4 мс для терминального участка a + a3 → (1/2)O2

митохондриальной электронпереносящей цепи. Эти значения получены для полностью восстановленных анаэробных митохондрий после импульсной подачи кислорода, т. е. определяют как раз переходные (кинетические) свойства переносчиков. Значение т ^2 = 0.4мс соответствует скорости переноса электронов ln2/ т _1/2 = 1.7 - 10 3 с ^{- 1} и току в расчете на перенос пары электронов (в силу квантового запрета, "один за другим") на кислород, равному приблизительно 5∙10^–16 А. Отметим также, что мембрана принципиально является источником тока, но не источником максвелловской сторонней электродвижущей силы (гальваническим элементом).

Условием квазиклассического приближения для мембраны и характера трансмембранного тока считается [16, с. 46–53 ] выполнение неравенства ^ ² = ( Й ²/ ( 2 m e A ф _m d m ) ) ^ 1, т. е. малость квантового масштаба действия Й по сравнению с величиной 2 m e Aф_md m , характеризующей потенциал ( m_e — масса электрона; Aф_m — трансмембранная разность потенциалов; d _m — толщина мембраны). При условии линейного хода потенциала в мембране, т. е. средней напряженности трансмембранного электрического поля A ф _m / d m = = 2 - 10⁷В/м ( A ф _m = 200 мВ; d _m = 100 А ), получаем ^ ² = 0.0015, и, следовательно, условие квазиклассичности выполняется. При нелинейном ходе потенциала (прямоугольный или трапецеидальный барьер) следует ввести характерную длину l <  d _m вблизи одной из межфазных границ "мембрана— водное окружение" или вблизи обеих границ. При подстановке вместо толщины мембраны d _m значения характерной длины менее l = 10 А квазикласси-ческое приближение перестает выполняться.

Другое условие квазиклассичности мембраны и электронного переноса следует из определения дебройлевской длины волны электрона X = h [ 2 m_e ( E - U ( x ) ) ] " ^V 2 ( E — полная энергия электрона; U ( x ) — потенциальная энергия электрона) и формулируется в виде неравенства [17, 18]

“ = -h- Г E - U (x )T - d dx   2 2me               dx

« 1.

Если считать, что E - U = A ф _m , т. е. избыточная (кинетическая) энергия электрона соответствует высоте потенциального барьера, то при l = d _m (линейный ход потенциала) получаем

— = 0.137 dx и, следовательно, выполнение квазиклассического условия. Однако при l = 10 A (dXdx = 1.37) более вероятно проявление квантовых свойств мембраны и туннелирование электронов. Соответственно в этом случае величина l обозначает длину туннелирования. Дебройлевская длина волны электрона может быть вычислена [17] непосредственно из выражения Xe = h[^3mekBT = 62 A, т. е. соизмерима с толщиной мембраны. Таким образом, ясно, что электрон не может быть локализован в активном центре донора (например, Fe2+). Это состояние благоприятно как с точки зрения обмена энергией с фононами гипотетической решетки (белком), так и с точки зрения легкости туннелирования.

Туннелирование электронов было постулировано при исследовании температурной зависимости проводимости прерывистых тонких металлических пленок на диэлектрических подложках [19]. При уменьшении внешнего смещения сохранялись однонаправленные (туннельные) переходы электронов, однако при близком к нулю, но конечном смещении такие переходы становились равновероятными в направлениях ± x , а ток проводимости — равным нулю. Приближение нулевого смещения послужило в этой работе доказательством существования туннельной проводимости. Исследуются также процессы, связанные с проводимостью (электронным транспортом) в металлопротеинах [20]. В этой работе, в частности, отмечается, что для одноступенчатого переноса электрона длина туннелирования не может превышать 20 Å .

Прозрачность прямоугольного барьера для туннельных электронов может быть рассчитана на основании формулы

- 1

D = ^ 1 +

( k^{2 +} Y 2 ) sh ( aY ) 2 _>  ² kY

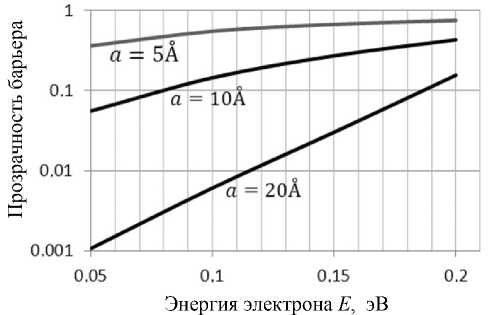
Прозрачность биологической мембраны для туннельного электрона при заданной длине a туннелирования

При равенстве высоты барьера и энергии электрона U ₀ = E e = 0.2эВ прозрачность с уменьшением ширины приближается к единице, а процесс переноса — к надбарьерному. Однако при E_e = 0.05эВ прозрачность тонкого барьера (5 A ) за счет туннелирования примерно в 500 раз больше, чем прозрачность более протяженного (20 Å ).

Высота барьера U ₀ = 0.2эВ = 8 k B T ( T = 300К ) позволяет оценить масштаб энергии, полученной электроном проводимости за счет обмена энергией с фононами гипотетической решетки донорного белка-переносчика. Прозрачность барьера при a = 5 A , как это следует из рисунка, равна приблизительно D = 0.75. Таким образом, в пределах барьера шириной a = 5 A средняя напряженность электрического поля равна E = 4 ■ 10⁸ В1м, т. е. в 20 раз больше значения, среднего для мембраны. Кроме того, наличие сильного поля у поверхности эмиттера делает барьер остроугольным и облегчает туннелирование.

Плотность мембранного туннельного тока можно оценить абиотически как плотность тока автоэлектронной эмиссии. В соответствии с формулой Фаулера—Нордгейма [21] запишем в которой k2 = 2meEe Ih2;

Y² = 2 m_e\E _e - U o| l h² ( E _e <  U о ) ;

J gg

e³E²      Г 8п2mn_e ( eАф ) ^3/2

------exp-----------— О 8nhe Аф           3 heE a — ширина барьера; Ee — энергия электрона; U0 — высота барьера, определяемая трансмембранной разностью потенциалов, т. е. U0 = eАфт = 0.2 эВ. Результаты расчетов представлены на рисунке.

где eАф — разность стандартных восстановительных потенциалов донорно-акцепторной пары белков-переносчиков электронов; О(у) — табулированная функция Нордгейма безразмерной переменной у = (e I eАф) eE 14пее0 . Используем значение e Аф для мембранной донорноакцепторной пары цитохромов b - c1, т. е. разность редокс-потенциалов 170мВ и соответственно eАф = 0.17эВ. При е = 2^3, т. е., в частности, при эмиссии в неполярный углеводород мембраны, а также и при е = 1, т. е. при эмиссии в вакуум, расчет при 0 (у) = 0 для обоих случаев дает характерное для автоэлектронной эмиссии высокое значение плотности тока J = Fg -Ng

= 1.46 - 10¹²A ■ м ^{- 2}. Это значение плотности тока следует понимать как импульсное, определяемое обменным временем туннелирования T t = 10 ^{- 14}с. Время переноса электрона, определяемое кинетикой электронпереносящей цепи, будем считать, как и ранее, равным т = 1/ ( 1.7 ■Ю³ ) = 5.9 ■ 10 ^{- 4}с. Здесь время τ следует понимать как сумму очень короткого, специфически квантового времени туннелирования τ_t и несоизмеримо более продолжительного времени релаксации белков-переносчиков, включая накачку донора, реорганизацию (конформационные перестройки) акцептора и миграцию энергии в среде-посреднике при переходе. Усреднение за время τ дает значение плотности тока j = 25A ■ м ^{- 2}, или в расчете на один дыхательный ансамбль площадью 5 ■ 10 ^{- 15}м² примерно 10 ^{- 13}А. Точно такой же расчет для ширины барьера a = 20 А и соответственно напряженности поля, равной Е = 10 8 В/м, дает среднее значение плотности туннельного тока около j = 1 A ■ м ^{- 2} и примерно 10 ^{- 14}А в расчете на один дыхательный ансамбль.

РАСЧЕТНЫЕ СООТНОШЕНИЯ И РЕЗУЛЬТАТЫ РАСЧЕТОВ

Для расчета термически активированного трансмембранного туннельного тока используем далее соотношения, полученные в работах [3, 14] и суммированные в монографии [22]. Квадрат интеграла перекрытия волновых функций электрона в потенциальных ямах донора и акцептора приближенно выражается в виде

I

e

= |j V X x)v_a ( x ) d x | ~ exp

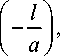
где величина a определяется соотношением a = й/ 2.^2 m e ( U - Е ) . Разность U - Е определяет высоту потенциального барьера, отсчитанную от дна ямы донора (в расчетах принята равной

U - Е = 0.6 эВ). Константа (частота) электронного переноса дается выражением

2П-- ¹V ^Г    „ exp [- ⁽ P-SS

й йго^2nS (2v +1)]      [ 2S(2v + 1)

эквивалентным уравнению Маркуса, в котором V = | Ee| • Ie — матричный элемент энергии взаимодействия электронов; E_e — электронный уровень донора, обозначаемый [14] как "энергия возмущения", отсчитанный от дна ямы и принятый в расчетах равным E_e = 6 k B T . Параметр P = А Е /( й го ) определяет "движущую силу" переноса, т. е. разность А Е стандартных восстановительных потенциалов переносчиков, которая принята равной А Е = 0.2эВ. Частота го нормальных колебаний, т. е. смеси фотонов и фононов, названной Хопфилдом [14] поляритонами, при расчете принята равной 3 ■ 10¹³с ^{- 1}, т. е. й го = 0.02эВ и соответственно P = 10, что соответствует мягким колебаниям. Параметр S = Е r /йго определяет энергию реорганизации Е r = ( 1/2 ) А ² й го .

Туннельный переход скачком изменяет положение донора и акцептора, а также и положение центра тяжести акцептирующей моды, т. е. всего массива атомов и групп, воспринимающих энергию перехода. Если r — расстояние между центром ямы акцептора электрона и центром тяжести акцептирующей моды до перехода, то мгновенный сдвиг центра тяжести при туннельном переходе определяется кулоновским соотношением А r = e ² ( 1 1 - r ) 2 /( 4 пее ₀ 1 1 ² r²Mro ²) , в котором e — заряд электрона; l ₁ — ширина потенциальной ямы донора; ε — микроскопическая диэлектрическая проницаемость, принимаемая равной е = 2; M , ω — масса и частота акцептирующей моды; Mω ² — жесткость осциллятора. Отношение А = А r/R0 ( R 0 — амплитуда нулевых колебаний, R 0 = 0.01 ^ 0.04 А) определяет энергию реорганизации и силу связи электрона в акцепторе: А «1 — слабая связь, энергия кванта й го ~ 0.1 ^ 0.2эВ и жесткие колебания; А »1 — сильная связь, энергия кванта й го ~ 0.01 ^ 0.02эВ и соответственно мягкие колебания. При расчете энергия реорганизации выбрана равной Е_г = 0.6эВ. Таким образом, S = 30, что соответствует сильной связи. Равенство U - Е = Е_г соответствует бездиссипативному (ква-зиупругому) характеру процесса реорганизации.

Параметр v = k B T/( Н го ) ( T = 300К) равен v = 1.3; длина туннелирования 1 принята равной 1 = 20 A .

Таким образом, получаем для вероятности переходов (числа переходов в секунду) значение k ET = 2.65 - 10¹³c ^{- 1}. Обратная полученному значению величина, т. е. время туннелирования одного электрона, составляет t , = 4 - 10 ^{- 14}c и соответствует временнόй (гейзенберговской) неопределенности. Трансмембранный ток в расчете на пару дыхательных переносчиков оказывается равным приблизительно i 1 = 4 - 10 — 6 A, т. е. несоизмеримо бόльшим по сравнению со сделанной ранее оценкой (10 ^{- 16}A), характеризующей кинетические возможности терминального звена дыхательной цепи. Однако усреднение тем же способом, каким это было сделано при оценке автоэлектронного тока, при условии T t << T 1 дает значение i 1 - ( t , / t ) = 4 - 10 ^{- 6} - ( 4 - 10 — 14/ 5.8 - 10 ^{- 4} ) = 3 - 10 ^{- 16}A Это значение соответствует плотности трансмембранного тока, равной приблизительно j = 0.06 A - м ^{- 2}.

При среднем (макроскопическом) значении напряженности трансмембранного электрического поля E = 2 - 10 7 B - м ^{- 1} из выражения j = oE (закон Ома) удельная электропроводность мембраны получается равной o = 3 - 10 — 9 ( Ом - м ) ¹. Наконец, из соотношения o = еп_ец_е при среднем значении подвижности ц _е = 10 ^{- 3}см²/(В • с ) (вычислена ниже) определяется концентрация носителей n e = 2 - 10 11 см ^{- 3}, соответствующая верхней границе для полимерных полупроводников (например, для нелегированного полиацетилена с проводимостью σ = 10^–8 (Ом·м)^–1). Вычислим далее подвижность электрона.

Выше отмечалось, что делокализованное положение электрона в теле мембраны способствует, во-первых, обмену энергией с фононами гипотетической решетки (белка) и, во-вторых, туннельным переходам (перескокам) по определенным точкам (узлам). Последовательность перескоков представляет собой марковский процесс, т. е. отдельные акты перескоков не коррелируют. Для этого формально требуется, чтобы время перескока было значительно меньше времени релаксации. Это условие легко выполняется для массивного белка-переносчика.

Предполагается [23, ч. II], что делокализованный электрон ведет себя, как классическая диффундирующая частица. С другой стороны, это предположение наталкивается на некоторые трудности. Классический радиус Лоренца диффунди- рующего электрона равен 2.8 -10-15м. Если же использовать формулу Стокса—Эйнштейна для коэффициента диффузии, в которую входят коммутативно радиус частицы и динамическая вязкость, и считать микровязкость мембраны равной П = 0.1Па - с (1пуаз) (экспериментально измерена для несоизмеримо более крупных частиц), то радиус оказывается равным 10-19м. Таким образом, остается принять, что формула Стокса— Эйнштейна неприменима.

Активационная вероятность перескоков определяется выражением we =(^2п)exp(-Ea/{kBT)), а одномерный (поперек мембраны) коэффициент диффузии — выражением D = ( 12/2)-(го/2п); пропорциональность частоте означает, что перескоки инициируются квантами колебаний решетки. Использование формулы Эйнштейна D = цekBT/е позволяет записать для подвижности соотношение е         el2 Нго